Experimental investigation on wave decay through vegetation patch with the quantitative generalized model of root, stem and leaf
-
摘要:目的 红树林作为一种新型生态式的护岸工具,其消波效应已成为海岸工程研究热点。本文对红树林根、茎、叶不同组成部分进行定量研究,进一步探究红树林对波浪的消减效应。方法 采取定量概化的根茎叶植物模型,通过波浪水槽试验探究了红树林植被区沿程波高衰减机制。将Kobayashi等提出的理论模型计算所得的植被区沿程波高理论值与试验值进行对比。结果 研究发现,由Kobayashi等提出的理论模型计算所得的试验波高衰减系数的范围分别为0.02 ~ 0.47。当入射波波长与植被区沿流向长度之比趋于1时,消波强度最弱。同时波浪在植被区衰减过程中出现了边界效应及波浪跃增现象,波高增量比的范围为0 ~ 13%。当波长与植被区沿流向长度之比在1.0 ~ 1.2之间,且淹没度等于1.0时,跃增高度随叶的分布密度的减小而增大,随根的分布密度的减小而减小。而当淹没度等于0.8时,减小根或叶的分布密度,跃增高度均减小。结论 根和叶的分布密度、淹没度以及波长与植被区沿流向长度之比均会对植被区沿程波高衰减规律产生不同程度的影响。Abstract:Objective Mangrove forest has become a research focus due to its functions as a newly ecological protector of shorelines. In order to quantify research the root, stem and leaf of mangrove forest, this study aims to experimentally investigate wave height decay along the quantitative generalized vegetation patch with root, stem and leaf.Method The wave height calculated by the formula of Kobayashi was compared with experimental data.Result The results showed that wave damping factors ranged from 0.02 to 0.47. The wave attenuation was lowest as the wave length of incident waves was equal to the length of the vegetation patch. And the boundary effect and wave height increment were observed as wave propagating over the vegetation patch. The relative wave height increment varied from 0 to 13%. When the submergence ratio ranged between 1.0 and 1.2, lower arrangement densities of leaves and roots resulted in higher and lower wave height increment, respectively. Additionally, the relative wave height increment was decreasing with a decreasing arrangement density of roots or leaves when submergence ratio equaled to 0.8.Conclusion The variation of wave height along the vegetation patch appears to depending on arrangement density, submergence ratio and wave length to the length of vegetation patch.
-
Keywords:
- wave height decay /
- root /
- leaf /
- distribution density /
- submergence rate /
- quantitative generalized plant model
-
板栗(Castanea mollissima)属于壳斗科(Fagaceae)栗属(Castanea)植物,是我国重要的木本粮食树种之一,其果实营养价值高,除富含淀粉外,还有蛋白质、脂肪、矿物质和维生素等营养物质,深受消费者喜爱,具有较高的经济价值[1]。目前我国板栗种植规模和总产量均居世界第一,但由于板栗喜光,枝条顶端优势强,结果部位外移快且自交不亲和,其结实率低,效益低下[2]。因此,培育具有优质、高产、短枝型等优良性状的板栗新品种具有重要的现实意义。
现阶段分子辅助育种已被广泛应用到植物育种工作中,但板栗新品种的培育仍以杂交育种为主[3],如:新品种‘明丰2号’(C. mollissima ‘Mingfeng 2’)是以‘燕明’(C. mollissima ‘Yanming’)为母本、‘燕山早丰’(C. mollissima ‘Yanshanzaofeng’)为父本杂交培育而来[4];‘南垂5号’(C. mollissima ‘Nanchui5’)则是以母本‘垂枝’(C. mollissima ‘Chuizhi’)与父本‘南沟1号’(C. mollissima ‘Nangou1’)杂交培育得来[5]。在杂交授粉过程中,如何提高成功率,以获取丰富的杂种资源是板栗育种亟待解决的问题。较高活性的花粉和柱头是授粉成功的关键[6],准确掌握花粉与柱头活性检测方法,探明其日变化规律,明确最适杂交授粉时间,可有效提高板栗杂交育种成功率。
目前,植物花粉活力检测方法多样,如2,3,5-三苯基氯化四氮唑(TTC)染色法、碘–碘化钾(I2-KI)法、MTT染色法、离体萌发法、墨水染色法等[7−9]。在柱头可授性检测方面,多数学者采用联苯胺–过氧化氢法[10−11]检测柱头可授性,部分研究采用MTT染色法[12]、直接授粉法等[13]。前期板栗花粉活力研究发现,不同板栗品种采用不同花粉活力测定方法,结果存在较大差异。陈可可[14]采用TTC染色法检测5个板栗品种花粉活力发现,‘泰安薄壳栗’(C. mollissima ‘Taianbaoke’)花粉活力最高可达72.18%;覃腾[15]以广西4个板栗品种为研究对象,采用离体萌发法检测其花粉活力,发现‘封开2号’(C. mollissima ‘Fengkai2’)萌发率最高,但仅为15.76%。在板栗柱头可授性研究方面,王倩[16]采用联苯胺–过氧化氢法检测了不同时期燕山板栗柱头可授性,发现盛花期柱头可授性最强;周晶[17]采用联苯胺–过氧化氢法检测板栗‘燕山红’(C. mollissima ‘Yanshanhong’)柱头可授性发现,柱头可授性高峰值出现于盛花期单日08:00—12:00。以上研究对花粉活力和柱头可授性的测定方法和日变化规律进行了初步探索,但并未将花粉活力、柱头可授性日变化规律与其坐果率、结实率、空苞率等进行综合分析。
为准确把握板栗最适授粉时间,提高板栗杂交育种成功率,为后期的良种培育提供充足的杂种资源,本研究首次以河北省迁西县主栽国审板栗品种‘燕山早丰’(果肉质地细腻、味香甜、熟食品质上等、丰产、质感效应较强)为母本[18−19],父本选择具有多粒、矮化等特异性状的‘王钱大栗’(C. mollissima ‘Wangqiandali’)、‘短枝芽变’(C. mollissima ‘Duanzhiyabian’)、‘三屯红栗’(C. mollissima ‘Santunhongli’),采用联苯胺–过氧化氢法、MTT法检测母本柱头可授性,采用TTC染色法、I2-KI法、醋酸洋红染色法、离体萌发法等检测花粉活力,通过研究盛花期花粉活力、柱头可授性、不同时间授粉对结实情况的影响,筛选‘燕山早丰’柱头可授性和杂交花粉活力的适宜检测方法,探明两者的日变化规律,筛选出最适杂交授粉时间。研究结果将为板栗人工杂交育种的成功提供理论指导,同时对解析板栗生殖生物学特性及繁殖机制具有重要意义。
1. 材料与方法
1.1 试验地概况
试验地位于河北省唐山市迁西县北京林业大学经济林(板栗)育种与栽培试验实践基地(40°18′ N,118°54′ E),属暖温带大陆性季风气候,年平均气温10.1 ℃,最低月平均气温−6.5 ℃,最高月平均气温25.4 ℃。年平均降水量817 mm,其中5—10月降雨量657.6 mm,占全年降水量的88%。年平均相对湿度59%,年平均无霜期176 d,全年日照2 581.5 h,日照充足。该地属于低山丘陵区,土壤质地为沙壤土,pH 6.44,有机质含量2.89 mg/g,土壤肥力为中等水平[20]。
1.2 试验材料
材料为11 年生板栗品种‘燕山早丰’‘王钱大栗’‘短枝芽变’‘三屯红栗’,长势优良,无病虫害,株行距4 m × 3 m,平均树高4.3 m,冠幅4.0 m × 4.5 m,树体为三主枝,开张角度 > 60°,树形为自然开心形。
1.3 研究方法
1.3.1 试验设计
参照周晶[17]研究结果,选择盛花期进行人工授粉。选取长势一致且健壮的板栗试验树60株,包括‘燕山早丰’45株,‘王钱大栗’‘短枝芽变’‘三屯红栗’各5株。40株‘燕山早丰’作为母本进行柱头可授性检测与授粉试验,5株‘燕山早丰’用于花粉活力检测;‘王钱大栗’‘短枝芽变’‘三屯红栗为父本,用于花粉活力日变化规律研究与授粉试验。各杂交授粉组合为 ‘燕山早丰’♀ × ‘王钱大栗’♂、‘燕山早丰’♀ × ‘短枝芽变’♂、‘燕山早丰’♀ × ‘三屯红栗’♂和1个自交组合‘燕山早丰’♀ × ‘燕山早丰’♂。
1.3.2 人工授粉
每授粉组合选择10株母树,每棵母树去雄套袋后,于盛花期单日08:00—18:00每隔2 h进行杂交授粉。采用随机区组设计,以单株为试验小区,共10个重复。各授粉组合每株母树每授粉时段在冠层中部东、南、西、北4个方向外围各均匀选取3个长势相近且健壮的雌花簇,1个授粉时段每母株共选取12个雌花簇,每个授粉组合每时段授粉120个雌花簇,4个组合共选取2 400个雌花簇。授粉时去掉套袋,用毛笔蘸取花粉轻轻点涂雌花柱头上,授粉完成后立即套袋。
1.3.3 花粉活力测定方法筛选
在上午08:00—10:00,采集‘燕山早丰’雄花盛花期的雄花序,每株树均从东、南、西、北4个方向取样,混合后分别采用TTC染色法[21]、醋酸洋红染色法[22]、I2-KI染色法[23]、离体萌发培养法[24]测定花粉活力,并以清水作为对照,筛选板栗花粉活力适宜检测方法。
1.3.4 花粉活力日变化规律研究
在08:00—18:00每隔2 h采集‘燕山早丰’‘王钱大栗’‘短枝芽变’‘三屯红栗’的雄花盛花期的花粉,选择1.3.3筛选出的花粉活力检测方法进行花粉活力日变化规律研究。
1.3.5 柱头可授性检测方法筛选
从40株‘燕山早丰’授粉母株中随机选取15株,在雌花盛花期每株树冠层中部东、南、西、北4个方向各均匀选取3个雌花簇,在上午08:00—10:00采集柱头,分别利用联苯胺–过氧化氢法[25]和MTT染色法[26]测定柱头可授性,并以清水作为对照,筛选板栗柱头可授性适宜检测方法。联苯胺–过氧化氢法判定标准:若柱头周围产生气泡数量多且体积较大,则柱头可授性很强(+++);若柱头周围产生大量小气泡,则柱头可授性较强(++);若柱头周围产生少量气泡,则柱头可授性较弱(+);若柱头无气泡产生,则柱头无可授性(−)。MTT染色法判定标准:若柱头具有可授性,则柱头被染成深蓝色或黑色,颜色由浅变深,柱头可授性由弱变强;若没有可授性,则柱头没有颜色反应。
1.3.6 柱头可授性日变化规律研究
在08:00—18:00每隔2 h采集‘燕山早丰’盛花期的柱头,选择1.3.5筛选出的柱头可授性检测方法进行柱头可授性日变化规律研究。
1.3.7 结实情况统计
授粉20 d后去除纸袋,使球苞自然生长,统计坐果率、落果率,9月上旬果实成熟后,计算结实率、空苞率。坐果率为未凋落雌花簇数与授粉雌花簇数的比值,落果率为凋落雌花簇数与授粉雌花簇数的比值,空苞率为空苞数与授粉雌花簇数的比值,结实率为果实成熟时的结实苞数与授粉雌花簇数的比值[15]。
1.4 数据分析
试验数据采用Excel软件进行整理,SPSS 26.0进行方差分析。
2. 结果与分析
2.1 花粉活力适宜检测方法筛选
花粉在清水处理的情况下,颜色均为淡黄色,接近半透明,分为形状规则的卵圆形与形状不规则两种形态(图1a)。0.5%和2%的TTC染色法的染色效果均不明显,延长染色时间后花粉依旧呈淡黄色(图1b,1c),故此方法不适合板栗花粉活力检测。醋酸洋红染色法效果明显,有活力的花粉呈鲜红色,形状呈规则的卵圆形,而无活力花粉未着色,体积小且形状不规则(图1d);该方法操作简单,染色时间短,效果好,有活力花粉与无活力花粉较易辨别,可作为板栗花粉活力检测方法。I2-KI染色法染色效果明显,有活力花粉颜色呈深棕色,无活力花粉不着色,但两者之间存在色浅、黄褐色的花粉,花粉活力较难判别,故此方法也不适合板栗花粉活力检测(图1e)。离体萌发培养法可以直接观察到花粉的萌发情况(图1f),可判断花粉是否具有活力,但花粉离体培养耗时较长,且培养条件较为严苛,易染菌,需要在无菌且温度恒定的环境下培养,花粉整体萌发率较低。
综合反应条件、反应时间、判断标准等方面,发现醋酸洋红染色法更适合进行板栗盛花期单日花粉活力规律研究。
2.2 不同板栗品种盛花期单日花粉活力变化规律
采用醋酸洋红染色法测定不同板栗品种单日内花粉活力变化规律,结果如表1所示。各品种盛花期单日内花粉活力均保持在75%以上,但不同品种板栗花粉在单日内不同时间活力存在差异。‘短枝芽变’和‘三屯红栗’单日内花粉活力波动较小,最高值均出现在10:00—12:00。‘燕山早丰’‘王钱大栗’单日内花粉活力波动相对较大,但花粉活力最高值也出现在10:00—12:00,最低值出现时段存在差异。其中,‘燕山早丰’10:00—12:00花粉活力显著高于16:00—18:00,‘王钱大栗’10:00—12:00花粉活力显著高于其余时间花粉活力。综上,以这4个品种为父本时,应该选择上午10:00—12:00采集花粉,此时花粉活力最高。
表 1 不同板栗品种盛花期花粉活力变化Table 1. Changes in pollen viability of different chestnut cultivars at full flowering stage% 时段 ‘燕山早丰’ ‘短枝芽变’ ‘王钱大栗’ ‘三屯红栗’ 08:00—10:00 84.78ab 90.47a 83.71b 88.58a 10:00—12:00 90.71a 91.32a 87.26a 88.97a 12:00—14:00 80.65ab 88.93a 75.34c 82.23a 14:00—16:00 81.14ab 90.63a 79.49c 83.76a 16:00—18:00 78.63b 86.89a 78.26c 80.53a 注:不同小写字母表示同一品种单日内不同时间花粉活力存在显著差异(P < 0.05)。下同。 2.3 柱头可授性适宜检测方法筛选
采用联苯胺–过氧化氢法检测‘燕山早丰’柱头可授性,由于板栗柱头形状结构限制,染色效果不佳,仅有柱头尖端可观察到轻微蓝色反应;但其表面气泡反应明显,区分度较高。柱头表面只产生少量气泡,且气泡体积较小,柱头可授性较弱,标记为+,记1分(图2a-1);柱头表面产生较多小气泡,柱头可授性较强,标记为++,记2分(图2a-2);柱头表面迅速产生大量气泡,且均匀附着整个柱头,柱头可授性最强,标记为+++,记3分(图2a-3)。
采用MTT染色法检测柱头可授性,短时间内柱头表面无明显颜色变化,避光染色1 h后,染色情况较为明显,有活力的柱头顶部变为黑色,且随着柱头可授性增强,染色长度逐渐增大。具体而言,仅有柱头尖端部分染色,染色面积微小,呈点状,此柱头可授性较弱(图2b-1);柱头尖端面积染色面积增大,其柱头底部也部分染色,即柱头可授性较强(图2b-2);柱头尖端染色部分延伸至柱头中部,且花柱上端也有部分染色,此柱头可授性极强(图2b-3)。
综上,联苯胺–过氧化氢法和MTT染色法都可以判断板栗柱头可授性强弱。综合考虑染色时长、可操作性等因素,在实际生产中,采用联苯胺–过氧化氢法检测板栗柱头可授性更适宜。因而,选择联苯胺–过氧化氢法进行板栗盛花期单日柱头可授性变化规律研究。
2.4 ‘燕山早丰’盛花期单日柱头可授性变化规律
表2显示:‘燕山早丰’盛花期单日内不同时段柱头均具有可授性,整体呈现出“上升—下降—上升—下降”的变化趋势。上午08:00—10:00柱头就已经具有较强可授性,10:00—12:00可授性达到最高,柱头表面具有大量气泡;随后急剧下降,12:00—14:00可授性要明显低于其他时段,之后可授性又重新升高,于14:00—16:00达到日变化第2个高峰,16:00—18:00可授性降低(图3)。
表 2 联苯胺–过氧化氢法检测‘燕山早丰’盛花期单日不同时间柱头可授性Table 2. Detecting single day stigma receptivity during full flowering period of ‘Yanshanzaofeng’ by benzidine-hydrogen peroxide method时段 柱头反应 柱头可授性 08:00—10:00 浸泡在溶液中3 ~ 5 min后,柱头表面出现大量气泡,且体积较大 +++ 10:00—12:00 浸泡溶液3 min左右,柱头表面出现大量气泡,气泡密集且体积较大 +++ 12:00—14:00 浸泡溶液5 min后,柱头表面出现少量气泡,体积较小 + 14:00—16:00 浸泡溶液5 min后,柱头表面出现气泡,气泡密集 +++ 16:00—18:00 浸泡溶液5 min后,柱头表面出现大体积气泡,但数量较少 ++ 注:+++. 柱头可授性极强;++. 柱头可授性较强;+. 柱头具可授性。 2.5 盛花期单日不同授粉时间对板栗结实情况的影响
各杂交组合中,不同时间授粉落果率与坐果率均无显著差异,但结实率与空苞率在不同授粉时间存在显著差异(图4)。 ‘燕山早丰’ × ‘王钱大栗’杂交组合在盛花期08:00—10:00与10:00—12:00时段授粉,其结实率分别高达79.30%与80.36%,显著高于12:00—14:00与16:00—18:00两个授粉时段(图4);且在10:00—12:00时段授粉,3粒坚果球苞结实率相较于其他授粉时段最高,达55.10%(表3);空苞率在10:00—12:00授粉时段最低,仅为14.74%,而16:00—18:00授粉时段的空苞率高达37.88%,二者差异达到显著水平。
表 3 各授粉组合盛花期单日不同时间授粉结实情况Table 3. Pollination and seed setting at different times of a single day during blooming period of each pollination combination授粉组合 授粉时段 结实率(1粒)/% 结实率(2粒)/% 结实率(3粒)/% 总结实率/% ‘燕山早丰’♀ × ‘王钱大栗’♂ 08:00—10:00 10.76a 14.71a 53.83a 79.30a 10:00—12:00 9.64a 15.62a 55.10a 80.36a 12:00—14:00 12.24a 17.78a 30.58b 60.60bc 14:00—16:00 5.21a 20.96a 44.24ab 70.42ab 16:00—18:00 12.35a 12.92a 29.86b 55.12c ‘燕山早丰’♀ × ‘短枝芽变’♂ 08:00—10:00 10.59a 8.07ab 40.69a 59.35a 10:00—12:00 4.98a 7.40ab 43.72a 56.10a 12:00—14:00 7.13a 3.25b 26.20ab 36.59b 14:00—16:00 5.67a 12.61a 34.56a 52.85a 16:00—18:00 7.28a 8.01ab 23.62ab 38.90ab ‘燕山早丰’♀ × ‘三屯红栗’♂ 08:00—10:00 3.25b 19.76a 53.41a 76.42a 10:00—12:00 10.60a 17.28ab 50.98a 78.86a 12:00—14:00 14.65a 17.31ab 29.02b 60.98ab 14:00—16:00 13.82a 17.32ab 39.06ab 70.20ab 16:00—18:00 11.38a 16.50b 29.02b 56.91b ‘燕山早丰’♀ × ‘燕山早丰’♂ 08:00—10:00 23.80a 4.70a 2.82a 31.32a 10:00—12:00 21.12a 4.17ab 2.50ab 27.79ab 12:00—14:00 17.63a 3.25ab 1.95ab 22.83ab 14:00—16:00 20.07a 3.96ab 2.38ab 26.40ab 16:00—18:00 16.84a 2.73b 1.64b 21.21b 注:不同小写字母表示同一授粉组合单日内不同时段授粉后结实情况存在显著差异(P < 0.05)。 在‘燕山早丰’ × ‘短枝芽变’杂交组合中,结实率在08:00—10:00授粉时段最高(59.35%),10:00—12:00时段的结实率与08:00—10:00时段相比略有下降(56.10%),并显著高于12:00—14:00授粉时段(图4);3粒坚果球苞结实率以10:00—12:00时段最高(43.72%)(表3);空苞率则以10:00—12:00授粉时段最低(27.64%),12:00—14:00与16:00—18:00的空苞率则高达46.34%与44.59%,均显著高于10:00—12:00(图4)。
在‘燕山早丰’ × ‘三屯红栗’杂交组合中,08:00—10:00、10:00—12:00授粉时段的结实率较高,达76.42%、78.86%,16:00—18:00结实率最低(56.91%),与上午差异达到显著水平(图4);3粒坚果球苞结实率以08:00—10:00时段最高(53.41%),10:00—12:00时段略有下降(50.98%)(表3);空苞率则在10:00—12:00授粉时段最低(8.94%),显著低于12:00—14:00和16:00—18:00授粉时段。
在‘燕山早丰’ × ‘燕山早丰’自交组合中,结实率均在30%左右(图4)。在08:00—10:00授粉时段,结实率最高(31.32%),空苞率最低(30.38%);在16:00—18:00授粉时段结实率最低(21.21%)(图4)。结实的球苞大多只含有1粒坚果,2粒坚果球苞与3粒坚果球苞结实率均以08:00—10:00最高,16:00—18:00最低;空苞率则以12:00—14:00最高,达53.54%(表3)。相比其他杂交组合,自交组合中的结实率较低,落果率与空苞率较高;但是结实率最高值出现在上午授粉时段,这与其他杂交组合相同(图4)。
综合不同板栗品种授粉组合在不同时时段授粉后的结实指标可以得出,结实率和3粒坚果球苞结实率最高值均出现在上午。因此,为提高板栗杂交授粉结实率,应选择上午进行板栗杂交授粉。
3. 讨 论
3.1 花粉活力检测
前人系统研究花粉活力发现,不同植物有不同的适宜检测方法。如:花生(Arachis hypogaea)花粉活力的最适检测方法为离体萌发法与红墨水染色法[7],薄壳山核桃(Carya illinoinensis)的花粉采用MTT染色法着色效果最佳[8],多花黄精(Polygonatum cyrtonema)的花粉活力最适检测方法为TTC染色法[27]。TTC试剂是依靠呼吸作用产生的NADH2或NADPH2对花粉进行染色。本试验中TTC试剂无法使板栗花粉着色,这可能是由于板栗自身呼吸作用产生的脱氢酶较少,无法达到理想的染色状态。此外,利用I2-KI对花粉进行染色时,染色效果会因直链淀粉与支链淀粉的比例不同而产生差异[28]。当花粉直链淀粉含量高时,会被试剂染为蓝色,如芝麻(Sesamum indicum)[23]、油茶(Camellia oleifera)[29];反之则为紫红色,如花生[7]、百合(Lilium lancifolium)[30]等。醋酸洋红染液则是根据花粉内物质积累量对花粉进行染色,正常花粉物质积累较多,对醋酸洋红的吸附作用与亲和力强,易被染为深红色,反正,呈淡红色或无色,如油菜(Brassica campestris)[31]。本研究中,醋酸洋红染色法、I2-KI染色法均可将‘燕山早丰’花粉成功染色,但是醋酸洋红染色法操作简单,染色快速,有活力花粉与无活力花粉易辨别,结果准确;而I2-KI染色法中存在浅色、黄褐色的介于有活力和无活力之间的花粉,活力界定具有主观性,花粉活力较难准确判别。因而,建议生产上使用醋酸洋红染色法检测‘燕山早丰’花粉活力。
3.2 柱头可授性检测
利用联苯胺–过氧化氢法检测柱头可授性,主要是依靠柱头表面有活力的过氧化氢酶,试剂中的过氧化氢在酶的作用下产生强氧化性的原子氧,将联苯胺氧化变色,并产生气泡。故当柱头表面气泡体积较大,数量较多时,柱头具有较强可授性,反之则柱头可授性较弱。此方法已广泛用于植物柱头可授性检验,如川贝母(Fritillaria cirrhosa)[32]、兜兰(Paphiopedilum)[33]等。MTT染色法检测柱头可授性主要依据柱头表面活性酶与试剂反应变色原理,可授性较强的柱头被染为深色,且染色面积较大,反之柱头颜色较浅[34−35]。本试验采用联苯胺–过氧化氢法和MTT染色法检验‘燕山早丰’的柱头可授性,其反应结果与其他植物基本相同,但MTT染色法检验板栗柱头可授性耗时较长,可能导致错过最适授粉时间。因此,在生产上可选取联苯胺–过氧化氢法快速检测柱头可授性,为杂交授粉提供指导。
3.3 花粉活力与柱头可授性日变化规律
花粉活力是决定授粉成功的重要因素,柱头是植物承接花粉的部位,二者对于准确把握植物授粉时间有重要意义,共同决定植物育种成功率[36]。不同植物的花粉活力与柱头可授性变化规律不同[23,37],因此,植物育种授粉前,应准确掌握花粉活力和柱头的变化规律,由此得到最适授粉时间,提高育种成功率。
本研究发现,上午08:00—12:00柱头可授性与花粉活力均较强,而在正午12:00—14:00柱头可授性较弱,且此时花粉活力显著降低,这可能与空气温度、湿度变化有关。板栗柱头为针状形,在雌花成熟过程中可观察到柱头尖端有蛋白质、脂类、多糖等分泌物溢出[38],中午温度升高,空气湿度降低,导致柱头分泌物内酶活性降低,柱头可授性降低。这与温度对甜樱桃(Prunus avium)柱头可授性的影响结果[39]相一致。此外,正午高温导致板栗花粉活力降低,这与辣椒(Capsicum annuum)的研究结果[40]相似。正午过后,气温降低,日照强度减弱,柱头内酶活性增强,柱头可授性与花粉活力回升;傍晚气温继续下降导致柱头可授性与花粉活力又重新降低。本研究得出的柱头可授性变化规律与周晶[17]对板栗柱头可授性的研究结果基本一致,且本研究中板栗花粉活力检测方法和变化规律方面的内容也弥补了板栗相关研究的缺失。
3.4 杂交授粉时间与结实情况
授粉时间显著影响授粉受精完成情况,如周建辉等[41]对厚皮甜瓜(Cucumis melo)进行不同时间杂交授粉,发现06:00—12:00授粉种子发芽率较高。对西瓜(Citrullus lanatus)[42]、西葫芦(Cucurbita pepo)[43]的研究也证实上午授粉比下午效果好,主要表现为坐果率较高,结籽数量多。此外,对玉米(Zea mays)进行不同时间授粉处理,发现不同自交系均在09:00—11:00和16:00—18:00授粉果穗的结实性状较好[44]。这与本研究得到的板栗08:00—12:00与14:00—16:00杂交授粉结实情况较好的结果相似,即最适授粉时间均避开了正午时段。除可以根据授粉结实情况筛选植物授粉时间外,也可根据柱头可授性和花粉活力筛选植物的适宜授粉时间。对青杨派树种进行柱头可授性检测,发现最佳授粉期为花序顶部露出芽鳞84 ~ 96 h[45]。本研究中,上午10:00—12:00进行授粉结实效果优良,这与前期柱头可授性与花粉活力变化规律的结果相符合,进一步验证了此时段为板栗最适杂交授粉时间。
通过将3个杂交授粉组合与自交授粉结实情况相对比,可以看出‘燕山早丰’存在明显的自交不亲和现象,其自交落果率与空苞率均较高,而结实率较低。不同杂交授粉组合间结实情况也存在差异,以‘王钱大栗’‘三屯红栗’为父本的授粉组合的结实率和3粒坚果球苞结实率与以‘短枝芽变’为父本的授粉组合存在较大差距,即存在明显的花粉直感效应,这与前人的研究结果[19]一致。后续在进行板栗杂交育种和种质优化时,宜选取性状优良的品种为父本,以丰富子代板栗优良性状。
4. 结 论
本研究首次以国审板栗品种‘燕山早丰’为试验对象,筛选其柱头可授性与花粉活力的高效便捷检测方法,并在此基础上以其为母本进行了多组合的分时段授粉,从而筛选出板栗适宜的杂交授粉时段。研究得到以下主要结论。
(1)板栗‘燕山早丰’柱头可授性最适检测方法为联苯胺–过氧化氢法,花粉活力最适检测方法为醋酸洋红染色法。
(2)盛花期单日内柱头可授性呈“上升—下降—上升—下降”趋势,且以10:00—12:00时间段柱头可授性最强,此时段不同父本板栗品种的花粉活力也最高。
(3)不同杂交组合中,总结实率与3粒坚果球苞结实率最高值均出现在08:00—12:00。
综合上述结果,实际生产中建议在上午10:00—12:00对‘燕山早丰’杂交授粉。研究结果不仅为优化板栗人工杂交授粉技术,提高板栗杂交授粉成功率,以获得充足的杂种资源提供了理论指导,同时有助于丰富板栗生殖生物学内容,揭示其繁殖机制。本研究设置的授粉试验时间梯度为2 h,在后续研究中可将时间梯度细化,以期筛选出更加精确的最适授粉时间,从而获得更理想的结实效果。
-
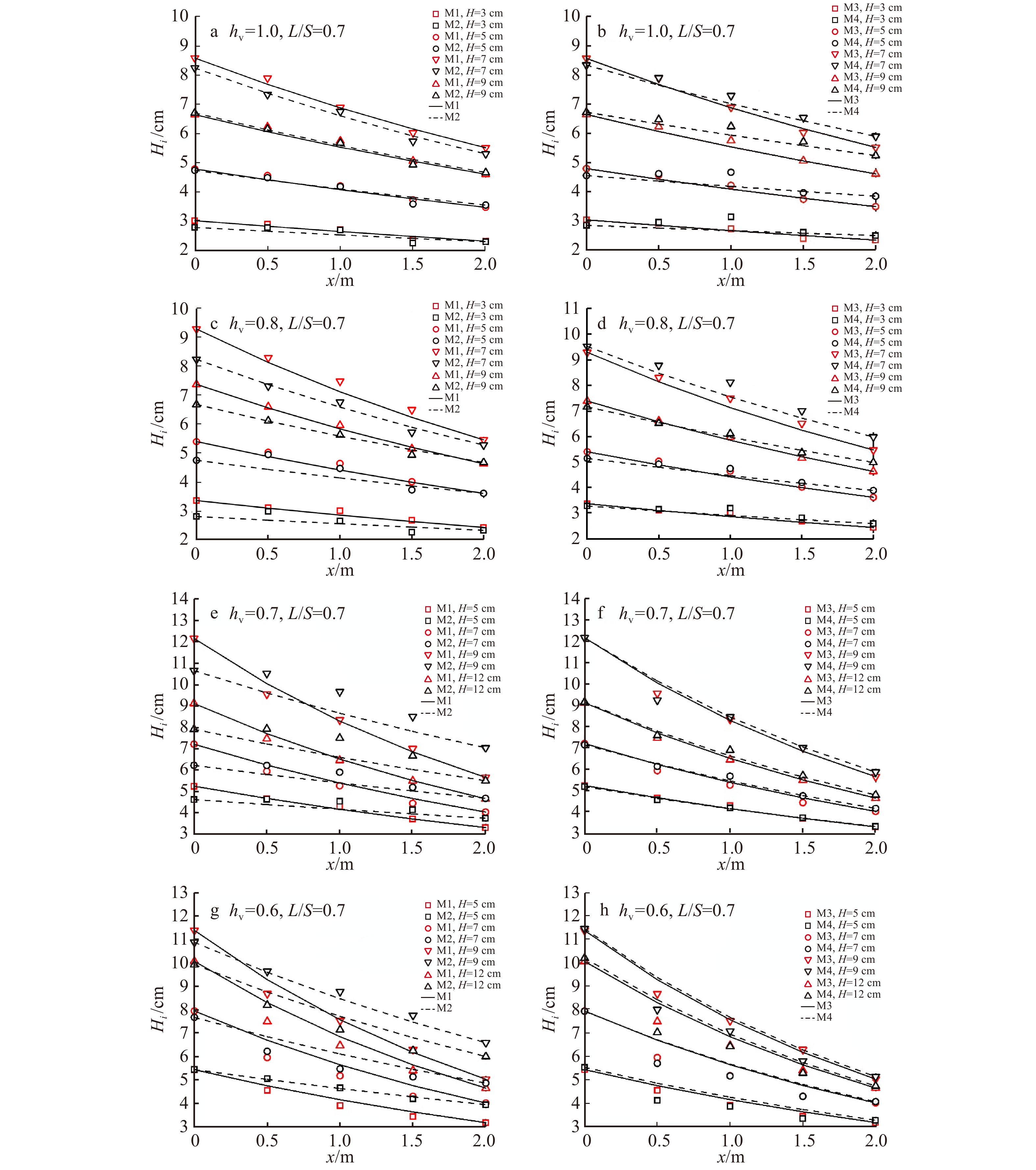
图 3 L/S ≤ 1.0时不同根和叶分布密度情况下的植被区沿程波高变化规律
hv. 淹没度;L/S. 波长和植被区长度的比值;实线:式(1)(Kobayashi等[20])计算得到的ψ2 = 30 根/株条件下波高变化理论值;虚线:由式(1)(Kobayashi等[20])计算得到的ψ2 = 16根/株条件下波高变化理论值。hv, submergence rate; L/S, wave length to the length of vegetation patch; solid line, theoretical value of ψ2 = 30 number/plant; dash line, theoretical value of ψ2 = 16 number/plant. The same below.
Figure 3. Variation law of wave height along the vegetation patch with different arrangement densities of roots and leaves with L/S all less than 1.0
表 1 试验工况
Table 1 Experimental cases
序号
No.根密度 /(根·株−1)
Root density (ψ1)/
(number·plant−1)叶密度/(根·株−1)
Leaf density (ψ2)/
( number·plant−1)试验水深
Experimental water
depth (h)/cm入射波高
Incident wave height
(H0)/cm入射波周期
Incident wave
period (T)/s模型1 Model 1 (M1) 30.0 30.0 25.0 3.0, 5.0, 7.0, 9.0 1.0, 1.5, 2.0 30.0 3.0, 5.0, 7.0, 9.0 35.0 5.0, 7.0, 9.0, 12.0 45.0 5.0, 7.0, 9.0, 12.0 模型2 Model 2 (M2) 30.0 16.0 25.0 3.0, 5.0, 7.0, 9.0 30.0 3.0, 5.0, 7.0, 9.0 35.0 5.0, 7.0, 9.0, 12.0 45.0 5.0, 7.0, 9.0, 12.0 模型3 Model 3 (M3) 16.0 30.0 25.0 3.0, 5.0, 7.0, 9.0 30.0 3.0, 5.0, 7.0, 9.0 35.0 5.0, 7.0, 9.0, 12.0 45.0 5.0, 7.0, 9.0, 12.0 模型4 Model 4 (M4) 16.0 16.0 25.0 3.0, 5.0, 7.0, 9.0 30.0 3.0, 5.0, 7.0, 9.0 35.0 5.0, 7.0, 9.0, 12.0 45.0 5.0, 7.0, 9.0, 12.0 -
[1] 陈玉军, 廖宝文, 黄勃, 等. 红树林消波效应研究进展[J]. 热带生物学报, 2011, 2(4):378−382. doi: 10.3969/j.issn.1674-7054.2011.04.017 Chen Y J, Liao B W, Huang B, et al. Progresses in the study of wave attenuation effect of mangroves[J]. Journal of Tropical Organisms, 2011, 2(4): 378−382. doi: 10.3969/j.issn.1674-7054.2011.04.017
[2] Dekker F. Hydrodynamics and morphodynamics in and around mangrove forests[D]. Enschede: University of Twente, 2006.
[3] Burger B. Wave attenuation in mangrove forests[D]. Delft: Delft University of Technology, 2005.
[4] 陈杰, 管喆, 蒋昌波. 海啸波作用下泥沙运动(Ⅴ):红树林影响下的岸滩变化[J]. 水科学进展, 2016, 27(2):206−213. Chen J, Guan Z, Jiang C B. Study of sediment transport by tsunami waves (V): influence of mangrove[J]. Advances in Water Science, 2016, 27(2): 206−213.
[5] Massel S R, Furukawa K, Brinkman R M. Surface wave propagation in mangrove forests[J]. Fluid Dynamics Research, 1999, 24(4): 219−249. doi: 10.1016/S0169-5983(98)00024-0
[6] Huang Z H, Yao Y, Sim S Y, et al. Interaction of solitary waves with emergent, rigid vegetation[J]. Ocean Engineering, 2011, 38(10): 1080−1088. doi: 10.1016/j.oceaneng.2011.03.003
[7] 陈杰, 何飞, 蒋昌波, 等. 植物消波机制的实验与理论解析研究进展[J]. 水科学进展, 2018, 29(3):439−451. Chen J, He F, Jiang C B, et al. Advances in laboratory experiment, theoretical analysis of mechanism of wave attenuation by vegetation[J]. Advancesin Water Science, 2018, 29(3): 439−451.
[8] Hashim A M, Catherine S M P. A laboratory study on wave reduction by mangrove forests[J]. Apcbee Procedia, 2013, 5: 27−32. doi: 10.1016/j.apcbee.2013.05.006
[9] Cuc N T K, Suzuki T, De Ruyter Van Steveninck E D, et al. Modelling the impacts of mangrove vegetation structure on wave dissipation in Ben Tre Province, Vietnam, under different climate change scenarios[J]. Journal of Coastal Research, 2013, 31(2): 340−347.
[10] Kathiresan K, Rajendran N. Coastal mangrove forests mitigated tsunami[J]. Estuarine Coastal & Shelf Science, 2005, 65(3): 601−606.
[11] 陈杰, 何飞, 蒋昌波, 等. 规则波作用下刚性植物拖曳力系数实验研究[J]. 水利学报, 2017, 48(7):846−857. Chen J, He F, Jiang C B, et al. Experimental investigation on drag coefficient of rigid vegetation influenced by regular waves[J]. Journal of Hydraulic Engineering, 2017, 48(7): 846−857.
[12] 陈杰, 赵静, 蒋昌波, 等. 非淹没刚性植物对规则波传播变形影响实验研究[J]. 海洋通报, 2017, 36(2):222−229. doi: 10.11840/j.issn.1001-6392.2017.02.014 Chen J, Zhao J, Jiang C B, et al. Laboratory on the effect of emergent rigid vegetation on the regular transformation[J]. Marin Science Bulletin, 2017, 36(2): 222−229. doi: 10.11840/j.issn.1001-6392.2017.02.014
[13] 何飞, 陈杰, 蒋昌波, 等. 考虑根茎叶的近岸植物对海啸波消减实验研究[J]. 热带海洋学报, 2017, 36(5):9−15. He F, Chen J, Jiang C B, et al. Experimental investigation on tsunami wave attenuation under the effects of coastal vegetation with root, stem and crown[J]. Journal of Tropical Oceanography, 2017, 36(5): 9−15.
[14] 何飞, 陈杰, 蒋昌波, 等. 考虑根茎叶影响的刚性植物消浪特性实验研究[J]. 水动力学研究与进展A辑, 2017(6):770−778. He F, Chen J, Jiang C B, et al. Experimental investigation on wave attenuation under the effects of rigid vegetation with root, stem and crown[J]. Journal of Hydrodynamics, 2017(6): 770−778.
[15] 何飞, 陈杰, 蒋昌波, 等. 植被区影响下孤立波沿程波高衰减特性试验[J]. 水利水电科技进展, 2018(1):75−82. doi: 10.3880/j.issn.1006-7647.2018.01.011 He F, Chen J, Jiang C B, et al. Experimental study on the characteristics of solitary wave height attenuation under the effects of vegetation belt[J]. Advances in Science and Technology of Water Resources, 2018(1): 75−82. doi: 10.3880/j.issn.1006-7647.2018.01.011
[16] 何飞, 陈杰, 蒋昌波, 等. 规则波作用下植物带波高衰减特性实验研究[J]. 海洋科学进展, 2017, 35(1):146−158. He F, Chen J, Jiang C B, et al. Experimental investigation on the characteristics of regular wave height attenuation in vegetation field[J]. Advances in Marine Science, 2017, 35(1): 146−158.
[17] 白玉川, 杨建民, 胡嵋, 等. 植物消浪护岸模型实验研究[J]. 海洋工程, 2005, 23(3):65−69. doi: 10.3969/j.issn.1005-9865.2005.03.011 Bai Y C, Yang J M, Hu M, et al. Model test of vegetation on the bank to attenuate waves and protect embankments[J]. The Ocean Engineering, 2005, 23(3): 65−69. doi: 10.3969/j.issn.1005-9865.2005.03.011
[18] 吉红香, 黄本胜, 邱秀云. 植物消波消浪研究综述[J]. 水利水运工程学报, 2005, 1(1):75−78. doi: 10.3969/j.issn.1009-640X.2005.01.015 Ji H X, Huang B S, Qiu X Y. Review on research of wave absorption by vegetation[J]. Hydro-Science and Engineering, 2005, 1(1): 75−78. doi: 10.3969/j.issn.1009-640X.2005.01.015
[19] Lima S F, Neves C F, Rosauro N M L. Damping of gravity waves by fields of flexible vegetation[J] Coastal Engineering, 2006, 2014, 5: 491−503.
[20] Kobayashi N, Raichle A W, Asano T. Wave attenuation by vegetation[J]. Journal of Waterway Port Coastal & Ocean Engineering, 1993, 119(1): 30−48.
[21] Sánchez-González J F, Sánchez-Rojas V, Memos C D. Wave attenuation due to Posidonia oceanica meadows[J]. Journal of Hydraulic Research, 2011, 49(4): 503−514. doi: 10.1080/00221686.2011.552464




 下载:
下载: