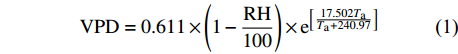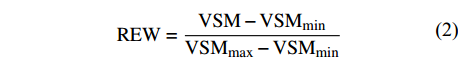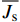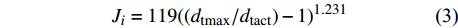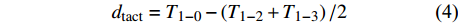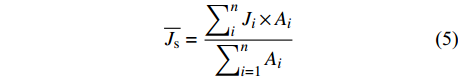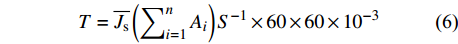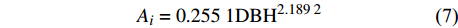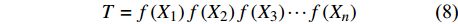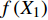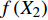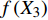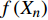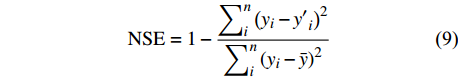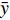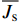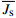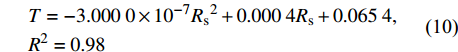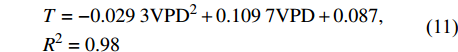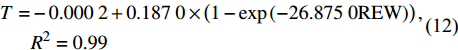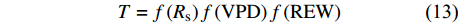长白山云冷杉针阔混交林林木空间利用率混合模型

李杨; 亢新刚

doi:10.12171/j.1000-1522.20190112

长白山云冷杉针阔混交林林木空间利用率混合模型

李杨,
亢新刚^,

北京林业大学林学院，省部共建森林培育与保护教育部重点实验室，北京 100083

基金项目: “948”国家林业局项目（2013-4-66）

详细信息

作者简介:
李杨，博士生。主要研究方向：天然林生长模型。Email：kitty.919@163.com　地址：100083 北京林业大学117信箱

责任作者:
亢新刚，教授，博士生导师。主要研究方向：天然林可持续经营。Email：xingangk@163.com　地址：同上

中图分类号: S758.5
计量
- 文章访问数: 2649
- HTML全文浏览量: 516
- PDF下载量: 74
出版历程
- 收稿日期: 2019-03-03
- 修回日期: 2019-03-16
- 网络出版日期: 2020-05-05
- 发布日期: 2020-06-30

Mixed model of forest space utilization in spruce-fir coniferous and broadleaved mixed forest of Changbai Mountains, northeastern China

Li Yang,
Kang Xingang^,

School of Forestry, Key Laboratory for Silviculture and Conservation of Ministry of Education, Beijing Forestry University, Beijing 100083, China

摘要

摘要:
目的建立林木空间利用率模型，为天然混交林中不同树种间生产力的比较提供依据，为单木成熟的判断提供参考。
方法利用林木生长量与树冠大小比值定义林木空间利用率，以长白山地区云冷杉针阔混交林为研究对象，基于20块标准地的2 268株单木数据，建立林木空间利用率混合模型，拟合各树种的空间利用率。
结果（1）备选指标中蓄积生长量和树冠投影面积之比与胸径相关系数最高，适宜作为计算指标。（2）通过逐步回归，最终选定林木胸径、胸径平方（代表胸高断面积）、树高、冠幅、样地蓄积、针阔比、坡向坡度、竞争指标作为林木空间利用率基础模型的自变量。（3）确定按树种分组，包含胸径平方及截距随机效应参数、指数函数异方差结构的混合模型，经检验，混合模型在建模数据及检验数据中的表现均略优于一般线性模型。（4）利用所构建的混合效应模型，对研究数据进行拟合预测，各树种空间利用率最高时期的胸径分别为云杉约40 cm，冷杉、落叶松、红松、中阔组约37 cm，慢阔组约32 cm。
结论林木利用率模型得到的数量成熟是以单位营养空间的生产力为基础的，使不同树种间的比较更为合理，且计算结果符合一般林学规律，可以作为该地区云冷杉针阔混交林判定单木成熟及优化林分结构的参考依据。
- 针阔混交林 /
- 林木空间利用率 /
- 线性混合模型 /
- 单木成熟 /
- 营养空间
Abstract:
Objective In this paper, the forest space utilization model was established to provide the basis for the comparison of productivity among different tree species in the natural mixed forest, and provide reference for the judgement of tree maturity.
Method The combination of tree growth and canopy size was used to define the forest space utilization. Based on the 2 268 individuals of 20 standard sites, which located in spruce-fir and broadleaved mixed forests in Changbai Mountain area of northeastern China, a mixed-effects model of forest space utilization was established to fit the spatial utilization of different species.
Result (1) The correlation coefficient between DBH and the ratio of volume growth to the crown projection area was the highest, so it is suitable to be the calculation index. (2) Through the stepwise regression, the tree DBH, DBH square (represent area), tree height, crown width, plot accumulation, proportion of coniferous trees, slope gradient and competition index were selected as the independent variables of forest space utilization. (3) Mixed effects model was developed, including the DBH square and intercept random effect parameters by species groups and the exponential function heteroscedasticity structure. The results showed that the mixed effects model was better than the general linear model both in the modeling data and the test data. (4) Using the mixed effect model to predict the research area data, the DBH of the highest spatial utilization of each tree species was obtained: spruce (Picea koraiensis) was about 40 cm; fir (Abies holophylla), Korean pine (Pinus koraiensis), larch (Larix olgensis), and medium-speed broadleaf trees were about 37 cm; slow broadleaf trees were about 32 cm.
Conclusion The mature DBH obtained from the forest utilization model is based on the productivity of the unit nutrient space, so that the comparison between different tree species is more reasonable. The calculation results are in accordance with the general forest rule, so it can be used as a reference to judge the tree maturity, optimize the stand structure in the coniferous and broadleaved mixed forest in that area.
- coniferous and broadleaved mixed forest /
- forest space utilization /
- linear mixed model /
- individual tree maturity /
- nutrient space

HTML全文

六盘山位于黄土高原西北部，不仅是干旱区−半干旱区的过渡区，也是黄土区−土石山区的过渡区，具有特殊的地理位置。华北落叶松是六盘山区的主要造林树种，在木材生产和水土保持方面发挥着重要的作用^[1]，但由于该地区气候梯度和年际波动大，降水分布不均，大面积造林虽然增加了植被覆盖率，却使区域生态耗水增加，河川径流减少^[2]，林水矛盾日益突出。森林蒸散是土壤−植物−大气系统（SPAC）中水热传输和能量转换的重要环节之一^[3-4]，是植被对干旱等环境条件响应的关键过程^[5-6]，其中，林分蒸腾是森林蒸散的最主要组分^[7]，约占 40% ~ 70%^[8]。因此，精确推算和预测林分蒸腾及其变化规律，揭示其与环境因子之间的关系，将有助于深入理解林水关系，并为当地植被恢复和林水管理提供理论指导。

以边材面积为空间纯量将树干液流进行尺度上推计算整株和林分蒸腾量的方法已经被广泛应用^[9-10]。但不同时间尺度下，影响树干液流的生态因子会发生显著变化，进而影响林木/林分蒸腾的变化。目前，对不同时间尺度林木/林分蒸腾对环境因子的响应已开展了一些研究，如张静等^[11]对苹果林的蒸腾研究发现，空气温度和饱和水汽压差均是日、月尺度下苹果林蒸腾的主要因子。李振华^[12]发现，潜在蒸散量可解释华北落叶松林分日蒸腾量变异的81%。Liu等^[13]发现林分日蒸腾量受潜在蒸散（PET）、叶面积指数（LAI）和不同深度土壤相对可利用水分（REW）的共同影响。王文杰等^[14]发现，随时间尺度的减小，影响树干液流的主要因子将由土壤环境因子（作用于根系的水分吸收）向大气因子如光照和空气湿度（作用于叶片气孔）转变。但这些研究多在日、年尺度下探讨林分蒸腾对单个或多个环境条件的响应，较少关注小时尺度林分蒸腾对环境因子的响应，同时缺乏小时尺度林分蒸腾对多因子响应的耦合模型。事实上，随着全球气候逐渐变暖，导致干旱加剧、短时和极端天气条件频发^[15]，日尺度上的研究无法揭示树干液流对日内剧烈变化的气象条件的响应，这将影响林分蒸腾的准确估计，限制对林木蒸腾响应环境变化的深入理解，因此有必要开展日内尺度的林分蒸腾的研究。因此，本研究以宁夏六盘山香水河小流域华北落叶松（Larix principis-rupprechtii）为研究对象，利用热扩散液流探针（SF-L）连续监测2018年生长季（5—10月）样树的树干液流，同步观测气象条件和土壤含水量，并拟合多因子影响的蒸腾模型，以期揭示短时间（小时）尺度内蒸腾对环境因子的响应规律，为当地林水管理提供理论依据。

1. 研究区概况

研究地点位于宁夏六盘山香水河小流域（106°12′ ~ 106°16′ E、35°27′ ~ 35°33′ N），面积为43.7 km²，海拔为2 070 ~ 2 931 m。该区属于温带半湿润气候，年均气温为5.8 ℃, 年均降水量为618 mm（1981—2010年）。主要土壤类型为灰褐土和高寒草甸土，其剖面主要分为枯落物层、腐殖质层、有机矿质层、淀积层和母质层^[16]，土壤砾石含量高，平均土层厚度约80 cm^[17]。人工纯林占小流域面积的24%，其中华北落叶松约占人工林总面积的90%。该小流域的分水岭沟子流域内华北落叶松均为同年栽植，经营历史相似，坡向均为东南坡向，因此，在该子流域选取一个水平坡长为425.1 m，平均坡度为27.8°的典型华北落叶松坡面，在坡脚处布设了一个长期固定监测样地，样地大小为30 m × 30 m，海拔为2 290 m, 坡度为37.6°。样地林分基本信息及0 ~ 80 cm土壤物理性质见表1。

表 1 研究样地基本信息

Table 1. Basic information of the study sample plot

平均胸径 Mean DBH/cm	平均树高 Mean tree height/m	平均冠幅 Mean crown width/m	林分密度/（株·hm^{− 2}） Stand density/ (tree·ha^{− 1})	郁闭度Canopy density	土壤密度 Soil bulk density/ (g·cm^{− 3})	总孔隙度 Total porosity/%	毛管孔隙度 Capillary porosity/%	非毛管孔隙度 Noncapillary porosity/%
18.71 ± 4.03	16.19 ± 2.34	3.27 ± 0.81	907	0.72	0.94	56.65	40.56	16.09

下载: 导出CSV

| 显示表格

2. 研究方法

2.1 气象条件监测

在距样地100 m处的林外空旷地安装一台WheatherHawk-232自动气象站（WheatherHawk，美国）记录气象条件，自计频率为5 min。测定的指标包括空气温度（T_a，°C）、空气相对湿度（RH，%）、降雨量（P，mm）、太阳辐射（R_s，W/m²）、风速（W_s，m/s）和风向。饱和水汽压差（vapor pressure deficit，VPD，kPa）由当时气温条件下空气中的饱和水汽压与实际水汽压之差计算而得^[18]：

${\rm{VPD}} = 0.611 \times \left( {1 - \frac{{{\rm{RH}}}}{{100}}} \right) \times {{\rm{e}}^{\left[ {\frac{{17.502T_{\rm{a}}}}{{T_{\rm{a}} + 240.97}}} \right]}}$

(1)

式中：T_a为空气温度（°C）；RH为空气相对湿度（%）。

2.2 土壤水分监测

根系层土壤水分对树木生长有重要作用，林木蒸腾直接受主根系层土壤水分的影响^[19]，而研究区华北落叶松根系层主要分布在0 ~ 60 cm^[20], 故本研究只关注根系层的土壤湿度。土壤湿度随土层深度变化有较大的空间变异^[20]，且变异程度随土层的增加而逐渐降低，所以需在不同土层深度布设探头，且在表层进行加密观测。鉴于此，在样地内按0 ~ 10 cm、10 ~ 20 cm、20 ~ 40 cm、40 ~ 60 cm土层深度布设土壤湿度、温度传感器（5TE，Decagon，美国），监测不同土层的土壤湿度动态变化规律。传感器与EM50（Em50，Decagon，美国）数据采集器相连，记录频率为 5 min一次。土壤可利用水分（relative extractable water，REW）的计算公式如下：

$\begin{array}{l} \;\\ {\rm{REW}} = \dfrac{{{\rm{VSM}} - {\rm{VS}}{{\rm{M}}_{\min}}}}{{{\rm{VS}}{{\rm{M}}_{\max}} - {\rm{VS}}{{\rm{M}}_{\min}}}} \end{array}$

(2)

式中：VSM为0 ~ 60 cm土层实际土壤含水量的平均值（m³/m³），VSM_min为0 ~ 60 cm土层的最小土壤含水量（m³/m³），VSM_max为0 ~ 60 cm土层的最大土壤含水量（m³/m³）。

2.3 树干液流的测定与计算

在样地内按树干径级（< 14 cm、14 ~ 17 cm、17 ~ 20 cm、> 20 cm）各径级选取1棵生长发育良好，无病虫害的树木做为样树用于监测树干液流，树干液流测定采用四针式热扩散液流探针（SF-L，Ecomatik，德国）。探针安装在树干北侧1.3 m处。安装探针时，首先将老化的树皮去除，将探针（S₁、S₀、S₂、S₃）按顺序插入树干内，注意加热探针（S₀）应位于上方。探针安装好后，用玻璃胶将探针与树干之间的缝隙密封，用铝箔纸将探针部位的树干包裹，防止雨水及环境热辐射对探针测定数据的影响。探针与数据采集器DL2e（Delta-T Devices，英国）相连，每5 min记录一次数据。

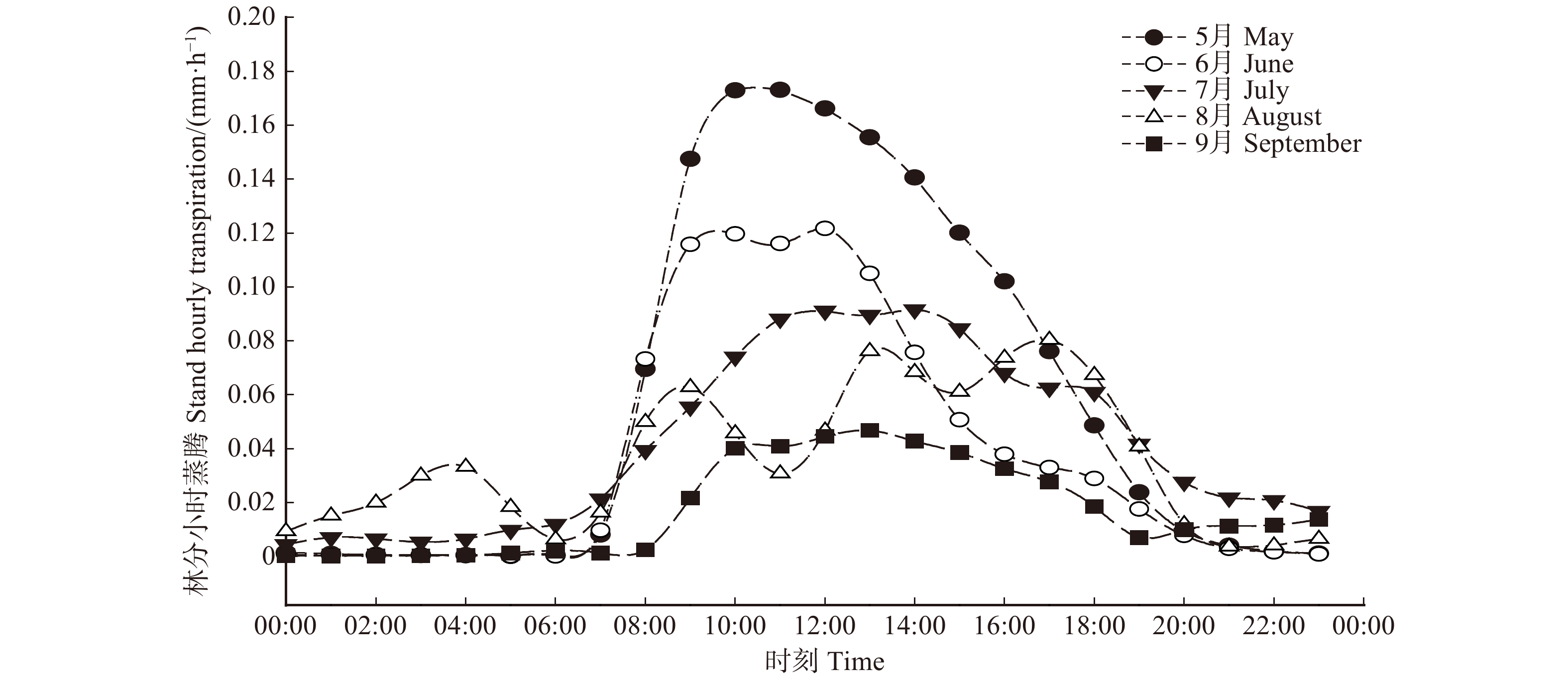
单株液流速率（J_i，g/（m²·s））及平均液流速率 $\overline {J_{\rm{s}}}$ （g/（m²·s））的计算方法为：

${J_i} = 119 {\left( {\left( {{d_{{\rm{tmax}}}}/{d_{{\rm{tact}}}}} \right) - 1} \right)^{1.231}}$

(3)

${d_{{\rm{tact}}}} = {T_{1 - 0}} - \left( {{T_{1 - 2}} + {T_{1 - 3}}} \right)/2$

(4)

$\overline {J_{\rm{s}}} = \frac{{\displaystyle\mathop \sum \nolimits_i^n {J_i} \times {A_i}}}{{\displaystyle\mathop \sum \nolimits_{i = 1}^n {A_i}}}$

(5)

式中：d_tmax为无液流时的最大温差（℃），即最大d_t值；d_tact为实际的d_t值（℃）；T₁₋₀、T₁₋₂、T₁₋₃分别为探针S₁与S₀、S₂、S₃之间的温度差（℃）。n为样树株数，A_i为第i株样树的边材面积（cm²）。

2.4 林分蒸腾量的计算

林分小时蒸腾量（T，mm/h）由样树的液流速率和边面积上推得到：

$T = \overline {J_{\rm{s}}} \left( {{\displaystyle\mathop \sum \nolimits_{i = 1}^n {A_i}}} \right) {S}^{-1} \times 60 \times 60 \times {10^{ - 3}}$

(6)

式中：S为样地面积（m²）。单株树干的边材面积A_i（cm²）由Liu^[13]基于边材面积与胸径之间的函数关系拟合得来，见公式：

${A_i} = 0.255 \; 1 {\rm{DB}}{{\rm{H}}^{2.189 \; 2}}$

(7)

2.5 数据处理

影响树木/林分蒸腾的环境因子众多，且各因素相互影响，很难区分出单个因素的影响。因此，本文使用上外包线法进行单因素分析，并剥离每个因素对蒸腾量的影响，该方法可在一定程度上消除其他影响因素的干扰^[21]。同时，假设各单因素对蒸腾量的影响是相互独立的，因此蒸腾量受各因素影响的耦合模型为其对每个单因素响应函数的连乘关系：

$T = f\left( {X_1} \right) f\left( {X_2} \right) f\left( {X_3} \right) \cdots f\left( {X_n} \right)$

(8)

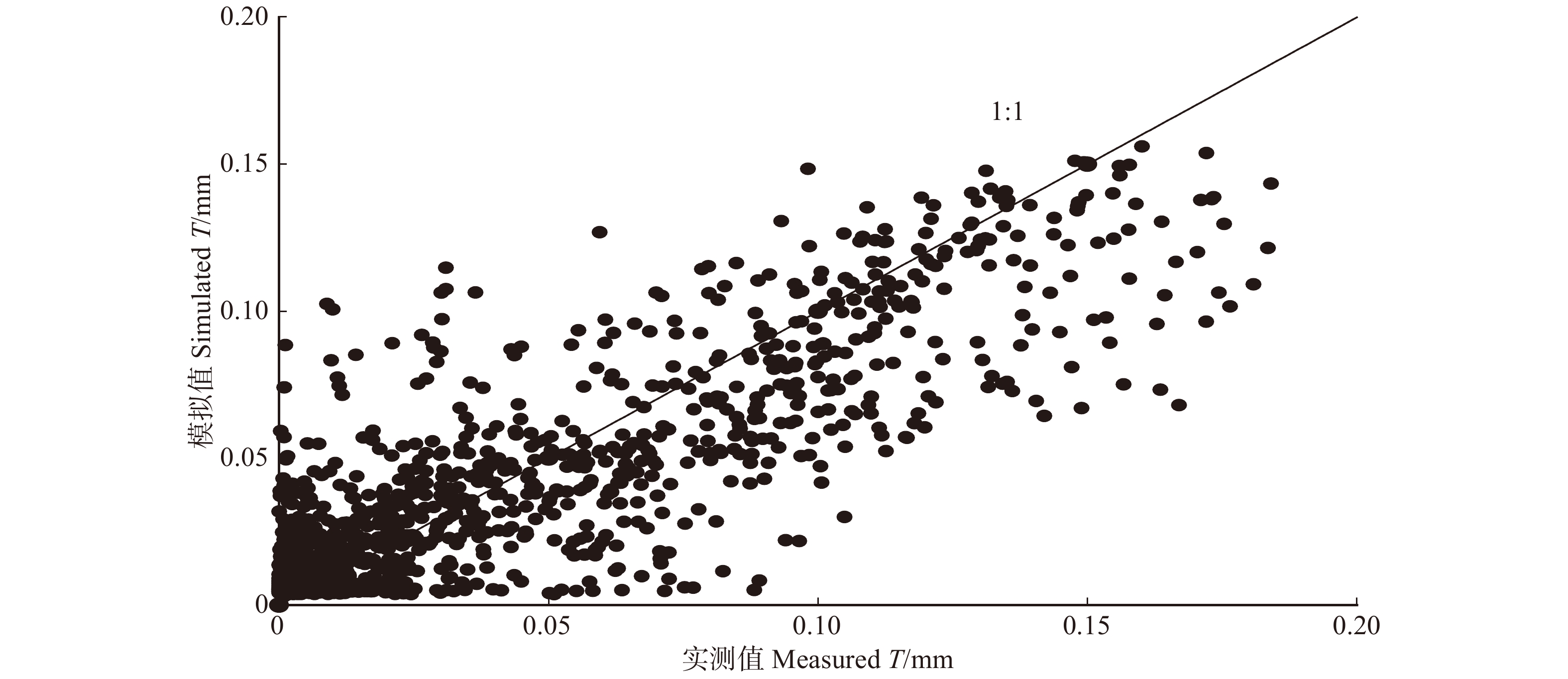
式中：T为林分蒸腾量， $f\left( {X_1} \right)$ 、 $f\left( {X_2} \right)$ 、 $f\left( {X_3} \right)$ ··· $f\left( {X_n} \right)$ 分别表示林分蒸腾量对单个因素的响应函数，n为因子数。

用R²和无量纲的纳什系数（NSE）来评价模型模拟的质量^[22]：

${\rm{NSE}} = 1 - \frac{{\displaystyle\mathop \sum \nolimits_i^n {{\left( {{y_i} - {{y'}_i}} \right)}^2}}}{{\displaystyle\mathop \sum \nolimits_i^n {{\left( {{y_i} - \bar y} \right)}^2}}}$

(9)

式中：y_i为实测值；y′_i为预测值； $\bar y$ 为所有实测值的平均值，NES越接近于1，表明模型拟合精度越高。

3. 结果与分析

3.1 环境因子的季节变化特征

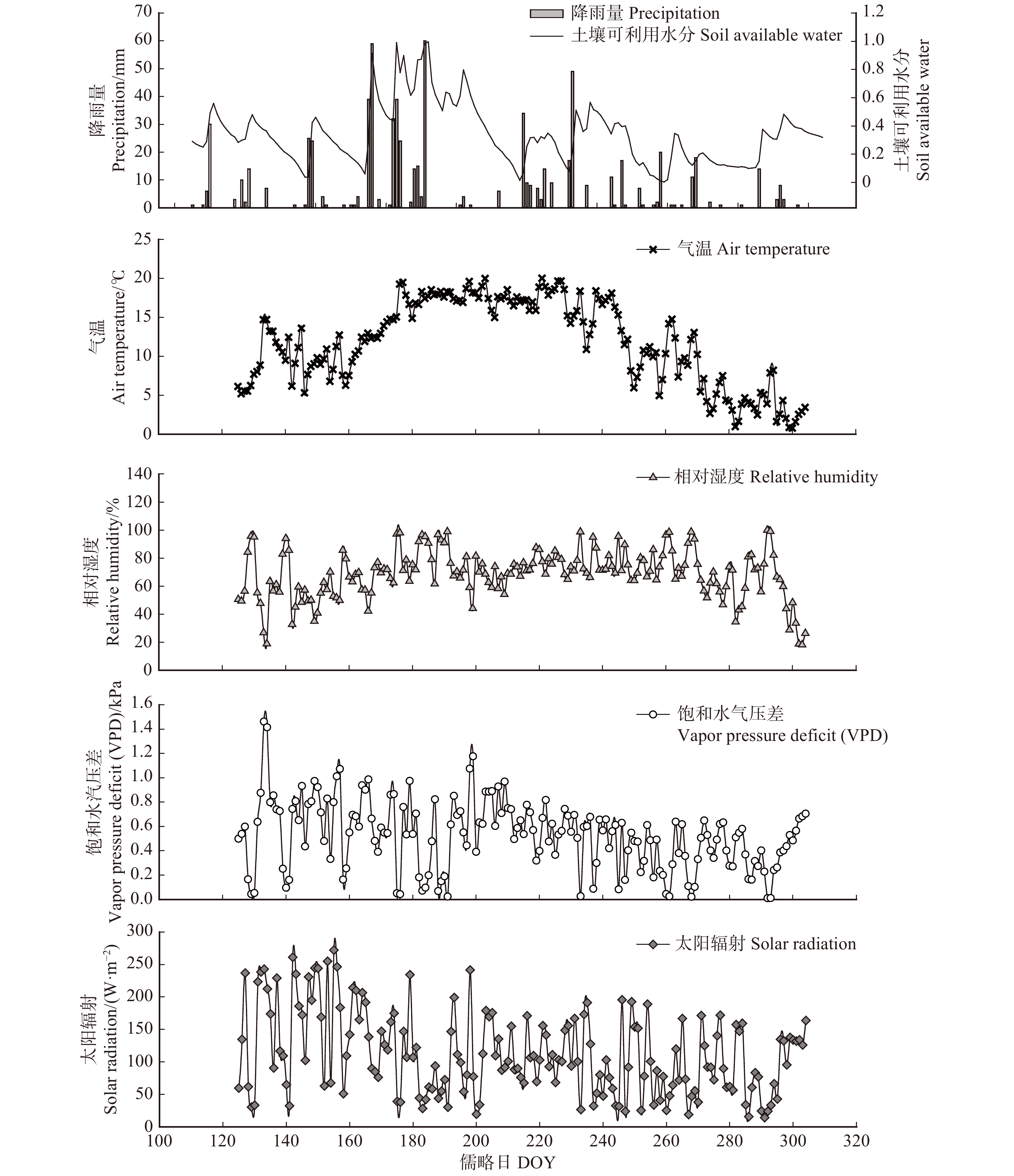
研究期间共观测到降水68场，累积降雨量为728 mm。降雨的季节动态呈单峰型变化格局，生长季初期（5月）和末期（9—10月）降水较少，6—8月降水较多。其中，6—8月总降水量占全年累计降水量的72%，最大的两场降雨分别发生在6月25日（59 mm）和7月10日（60 mm）。观测期间土壤相对可利用水分（REW）的变化范围为0.003 ~ 0.997，平均值为0.337。REW在6月25日至7月26日之间保持较高水平，与该时间段内连续的强降雨事件有关。分析数据发现，降水事件后的第2天，REW会大幅度升高，说明REW对降雨的响应存在一定程度的滞后。日均气温的变化趋势表现为随儒略日（DOY）的增加先升后降，变化范围为0.79 ~ 20.03 ℃，平均值为11.71 ℃，月均值表现为7月最大（17.75 ℃），10月最小（3.72 ℃）。观测期间空气相对湿度呈先增后减的变化趋势，变化范围为18% ~ 100%，平均值为68.3%。饱和水汽压差（VPD）的变化范围为0.01 ~ 1.46 kPa，平均值为0.53 kPa；太阳辐射强度（R_s）的变化范围为14.02 ~ 272.23 W/m²，平均值为113.96 W/m²，二者的月均值均表现为5月最大（0.66 kPa，160.6 W/m²），9月最小（0.36 kPa，87.41 W/m²）。2018年生长季环境因子的变化规律见图1。

图 1 2018年生长季内环境因子变化

Figure 1. Variations of environmental factors in growth season of 2018

下载: 全尺寸图片幻灯片

3.2 树干液流速率及林分蒸腾的日内变化

华北落叶松叶片在10月份会变黄并逐渐脱落，为减小叶片活性对数据的影响，选择2018年5—9月连续3个晴天（27日，28日，29日）的液流值，分析生长季不同时期华北落叶松树干平均液流速率（ $\overline {J_{\rm{s}}}$ ）的日进程。由图2可知，液流速率存在明显的日变化，在一天内呈现单峰或多峰的变化特征，且不同时期树干液流的启动和停止时间不尽相同。5月27日至29日，树干液流于早晨06:50—07:05之间启动，之后迅速增加，至10:15—11:45之间达到峰值后开始下降，直至夜晚22:05—23:00之间达到最低值。6月27日至29日树干液流的启动时间为06:45—07:25之间，达到峰值的时间为10:50—12:25，出现最低值的时间为21:45—23:35。7月液流开始启动和停止的时间分别为03:40—07:00和21:05—23:00；9月液流的启动时间和停止时间分别为07:05—08:20和20:45—23:10。但8月27—29日树干液流的日进程与其他月份不同，存在夜间液流的现象。由于夜间气孔关闭，蒸腾作用停止，此时液流活动主要用于补充白天因强烈的蒸腾而导致的树体内的储水量减少的那部分水分^[23-24]。同时，受不同时期土壤水分条件和气候条件的影响，树干液流峰值的大小从5—9月呈逐渐变小的趋势。

图 2 典型晴天树干液流速率的日进程

Figure 2. Diurnal variations of sap flux density (

$\scriptstyle \overline {J_{\rm{s}}}$ ) in typical sunny days

下载: 全尺寸图片幻灯片

利用公式6计算得到林分小时蒸腾，将每月连续3天相同时刻的林分小时蒸腾进行平均，结果见图3。由图3可知，林分小时蒸腾的日内变化规律与树干液流速率基本相同，均呈单峰或者多峰的变化。尽管5—8月，林分蒸腾均从早上07:00开始出现，但生长季初期（5月和6月）林分蒸腾增加到最大值的速度要快于其他月份，而9月份林分蒸腾在早上8:00出现，要晚于其他月份。林分小时蒸腾量的峰值（mm/h）表现为5月（0.173）> 6月（0.122）> 7月（0.916）> 8月（0.762）> 9月（0.468）。

图 3 不同月份内林分小时蒸腾的日内变化特征

Figure 3. Diurnal variations of stand hourly transpiration (T) in different months

下载: 全尺寸图片幻灯片

3.3 林分小时蒸腾对单因素环境条件的响应

在小时尺度上，林分蒸腾的变化主要受VPD^[25]、R_s^[25]和REW的影响，因此，本文选取R_s、VPD和REW为主要影响因子，基于上外包线分析2018年生长季奇数天林分蒸腾量与R_s、VPD和REW的关系，逐个确定其响应函数。

图4为林分小时蒸腾（T）与R_s的外包线关系，由图可知，林分小时蒸腾对R_s的响应呈二次函数关系，可表示为：

图 4 林分小时蒸腾对太阳辐射的响应

Figure 4. Response of stand hourly transpiration (T) to solar radiation

下载: 全尺寸图片幻灯片

$\begin{aligned} & T = - 3.000 \; 0 \times {10^{ - 7}}{R_{\rm{s}}}^2 + 0.000 \; 4{R_{\rm{s}}} + 0.065 \; 4, \\ & {{R^2} = 0.98} \end{aligned}$

(10)

当R_s较小时，林分蒸腾随R_s的增大而增大，当R_s达到666.7 W/m²后，林分蒸腾随R_s的继续增大而减小。这是因为当R_s较小时，随着R_s的增大，气孔因受到光照的诱导作用而打开；同时空气温度升高，叶面温度也随之升高，为植物的蒸腾提供了能量^[26]。而当R_s继续增大时，气孔会因为温度过高而关闭，使得蒸腾量减小。

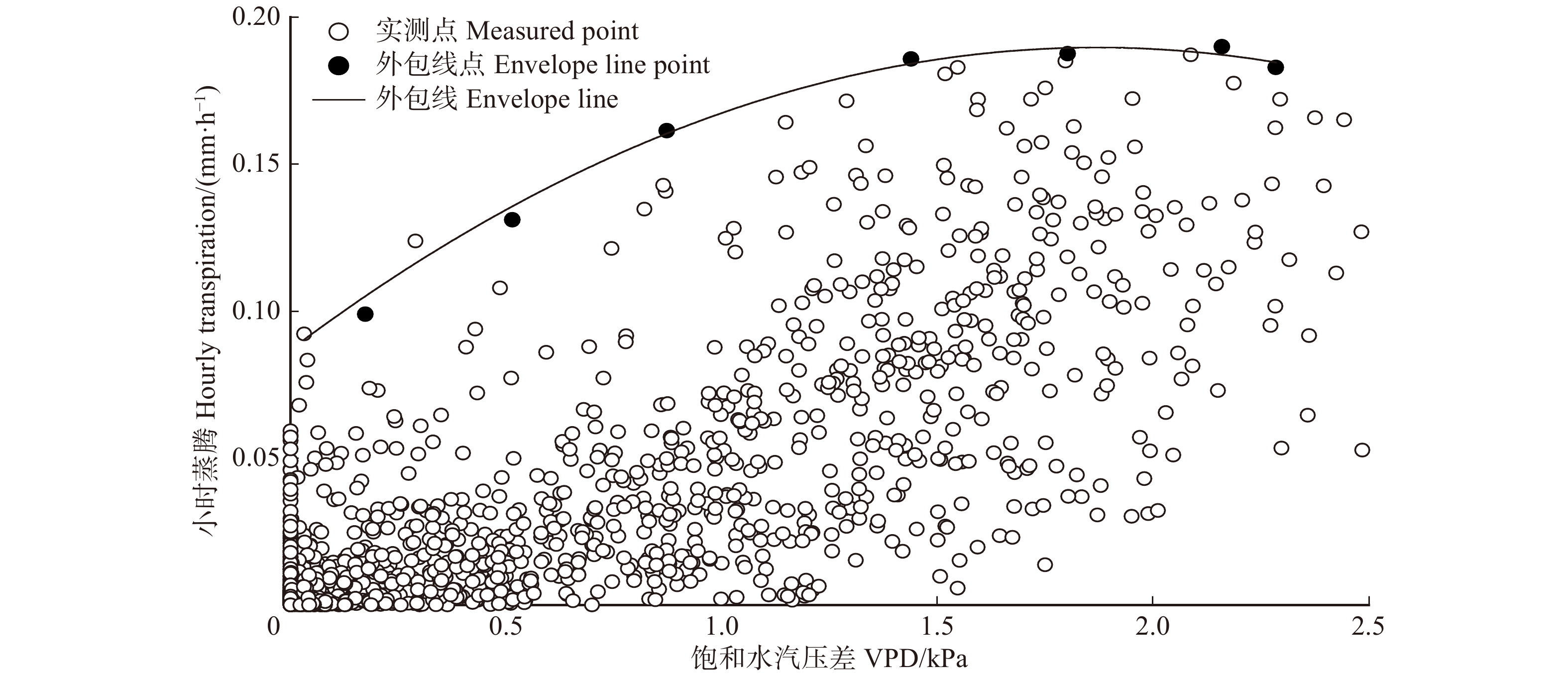
图5为林分小时蒸腾与VPD的外包线关系，由图可知，林分小时蒸腾与VPD的响应呈二次函数关系，其外包线函数关系为：

图 5 林分小时蒸腾对饱和水汽压差的响应

Figure 5. Response of stand hourly transpiration (T) to vapor pressure deficit

下载: 全尺寸图片幻灯片

$\begin{aligned} & T = - 0.029 \; 3{\rm{VP}}{{\rm{D}}^2} + 0.109 \; 7{\rm{VPD}} + 0.087 ,\\ & {{R^2} = 0.98} \end{aligned}$

(11)

当VPD小于1.86 kPa时，林分蒸腾随VPD的增大而增大，当VPD大于1.86 kPa后，林分蒸腾随VPD的增大而减小。这是因为VPD过高时，植物将缩小气孔开度，减少水分过渡耗失，防止叶片水势过低而造成木质部出现灾变性的功能失衡^[27]，但这将使气孔导度下降，蒸腾减小。

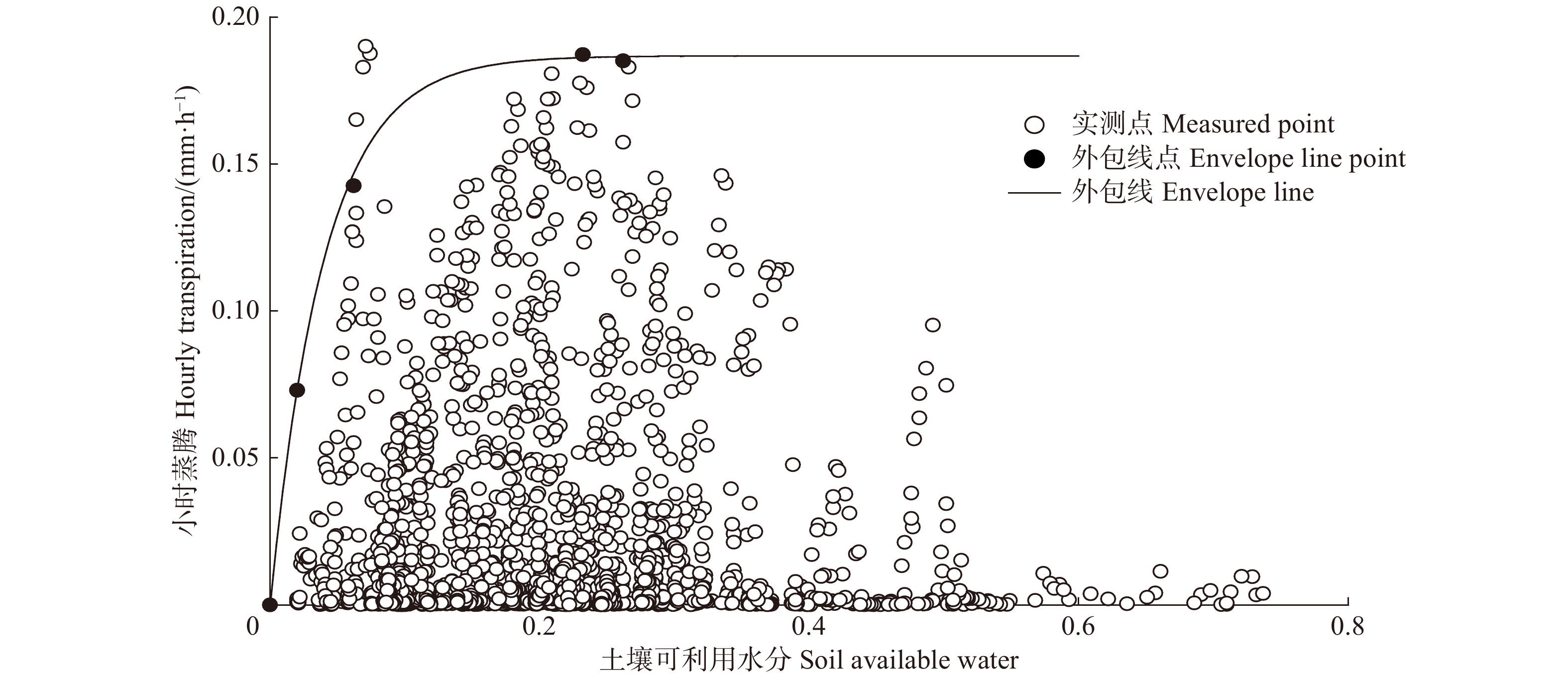
林分小时蒸腾与REW的外包线关系如图6所示。可以看到，林分小时蒸腾与REW的关系符合趋于饱和的指数方程，其外包线关系为：

图 6 林分小时蒸腾对土壤可利用水分的响应

Figure 6. Response of stand hourly transpiration (T) to relative extractable water

下载: 全尺寸图片幻灯片

$\!\begin{aligned} T = & - 0.000 \; 2 + 0.187 \; 0 \times \left( {1 - {\rm{exp}}\left( { - 26.875 \; 0{\rm{REW}}} \right)} \right),\\ & {{R^2} = 0.99} \end{aligned}\!\!\!\!\!\!\!\!\!\!\!$

(12)

林分蒸腾先随REW的增大而快速增加，当REW增加至0.3后，林分蒸腾增加的速度减缓并逐渐趋于稳定。这是因为当REW较小时，叶片水势低，水分由根系向上传递的驱动力弱，水分传输受阻；而随着REW的增加，树木可以吸收的水分和叶片水势增加，蒸腾速率也随之增加^[28]；当REW增加到某一阈值时，蒸腾量逐渐趋于稳定。

3.4 林分小时蒸腾对多因素的响应及耦合模型

为反映R_s、VPD和REW对林分小时蒸腾的综合影响，基于公式10 ~ 12的函数形式和连乘方程（公式8），得到样地小时蒸腾对R_s、VPD和REW响应的耦合模型基本形式：

$T = f\left( {{R_{\rm{s}}}} \right) f\left( {\rm{VPD}} \right) f\left( {\rm{REW}} \right)$

(13)

进一步利用2018年生长季奇数天的实测数据进行重新拟合模型参数。得到模型表达式为：

$\begin{aligned} T = &\left( { - 6.347 \; 0 \times {{10}^{ - 5}}{R_{\rm{s}}^2} - 0.637 \; 0{R_{\rm{s}}} - 208.734 \; 8} \right) \times \\ &\left( { - 0.003 \; 2{\rm{VP}}{{\rm{D}}^2} + 0.013 \; 8{\rm{VPD}} + 0.001 \; 7} \right) \times \\ & \left( { - 0.008 \; 1 - 0.004 \; 6\left( {1 - {\rm{exp}}\left( { - 12.469 \; 6{\rm{REW}}} \right)} \right)} \right),\\ & {R^2} = 0.74 \end{aligned}$

(14)

利用该模型（公式14）得到的模拟值（2018年奇数天）与实测值具有较高的吻合性，（R² = 0.74，NSE = 0.82）。利用未参与模型拟合的偶数天数据对模型进行验证发现（图7），模拟值与实测值的吻合较好（R² = 0.77，NSE = 0.84），表明该模型能较好的模拟小时尺度林分蒸腾对环境变化的响应。

图 7 小时尺度林分蒸腾实测值与模拟值对比

Figure 7. Comparison between the measured and simulated stand hourly transpiration (T)

下载: 全尺寸图片幻灯片

4. 讨　　论

4.1 林分小时蒸腾对单因素环境条件的响应

在小时尺度上，林木/林分蒸腾对R_s和VPD的响应最为敏感，R_s是调节气孔活动的主要环境因子，而VPD是林分蒸腾的主要驱动力^[29]。研究表明，蒸腾速率与R_s，VPD显著相关^[30-33]。VPD表示空气的干燥程度^[34]，当VPD较低时，气孔导度与VPD呈正相关；当VPD上升到一定阈值后，二者呈负相关。气孔对VPD的这种响应机制增加了从土壤到叶片这条水流通路上的导水阻力，保证了树木自身用水安全^[32]。林分蒸腾响应VPD阈值的大小因树种而异。韩路等^[35]对塔里木盆地灰胡杨（Populus pruinosa）的研究发现，蒸腾速率对VPD的响应阈值为2.92 kPa；贾国栋等^[36]发现北方土石山区油松（Pinus tabuliformis）和刺槐（Robinia pseudoacacia）林分蒸腾在VPD达到1.1 kPa后降低。Fletcher等^[37]发现VPD阈值受到植物耐旱程度的影响，一般在0.8 ~ 2.0 kPa。李新宇等^[38]对银杏的蒸腾耗水研究表明，当VPD < 3.2 kPa时，VPD对液流是驱动作用，而VPD > 3.2 kPa时转变为限制作用。本研究中，当VPD于1.86 kPa后，林分蒸腾开始减小，该响应阈值在Fletcher等的研究结果范围之内。R_s影响气温和相对湿度，而VPD是温度和相对湿度的函数，因此，R_s的改变会引起VPD的改变。强太阳辐射使气温升高，空气相对湿度下降而导致VPD增大，引起气孔导度下降从而使林分蒸腾降低，因此，林分蒸腾对R_s的响应也存在一个阈值。朱丽薇等^[39]研究发现当VPD大于2 kPa，同时光合有效辐射大于1 000 μmol/ （m²·s）时，荷木冠层气孔导度与水汽压亏缺呈显著负相关，说明辐射与水汽压亏缺共同决定气孔开闭。因此，R_s与VPD对蒸腾的影响是相互作用的。

除气象条件外，土壤水分也是影响树木蒸腾的主要因子。研究发现，樟子松在土壤水分偏低时，对R_s和VPD的敏感程度会降低，此时，REW成为主要的限制因子^[40]。REW表征土壤供水能力的大小，林木蒸腾的水分主要来自于植物根系从土壤中吸取的水分，因此，植物是否受到干旱胁迫主要是由土壤水分的可利用性决定，并不完全取决于降雨条件^[32]。土壤水分不足时，气孔为了降低干旱造成的风险会关闭^[41]，导致液流速率下降，蒸腾量降低。Orlandini等^[42]通过研究盆栽葡萄（Vitis vinifera）对土壤干旱的响应发现，当REW降低至0.35时，蒸腾速率开始降低。Lagergren 和Lindroth^[43]在瑞典中部的针叶混交林内研究发现，树木蒸腾出现明显降低的REW阈值在0.2左右。当土壤水分充足时，叶片水势增加，蒸腾速率表现为先增加后逐渐趋于稳定的变化趋势^[12]。有研究表明，林分蒸腾达到稳定时的REW的阈值为0.2 ~ 0.5之间^[44]。本研究中，当REW的阈值大于0.3 时，林分小时蒸腾基本保持稳定，该阈值在前人研究的阈值范围之内。

4.2 多因素共同影响下的树木蒸腾

在自然条件下，树木蒸腾受大气蒸腾需求和土壤水分可获得性的共同限制。因此，精确量化各环境因子对蒸腾的影响，并建立多因素影响的林分蒸腾模型非常有必要。利用上外包线法和连乘方程构建多因素对林分蒸腾影响的复合模型，可较好地模拟林分蒸腾^[12,44]。但目前研究均集中在日尺度上，对短时间尺度（如小时尺度）上树木蒸腾对多个环境的响应关系及耦合模型还未见报道，这限制了对树木蒸腾响应短时间环境变化的准确理解。本研究在小时尺度上建立了同时反映R_s，VPD和REW影响的华北落叶松林分蒸腾模型，具有较高的拟合精度，可解释小时蒸腾量变异的74%，可为更进一步理解华北落叶松蒸腾对小时尺度上环境变化的响应提供帮助。但本研究建立的耦合模型并未考虑短时间尺度下树干液流对R_s和VPD的响应的时滞效应问题。Zeppel等^[45]对澳大利亚桉树（Eucalyptus crebra）和白羽松（Callitris glaucophylla）的研究发现，树干液流对VPD的响应关系会出现顺时针方向的时滞圈；Hong等^[6]发现，树干液流速率对R_s的响应在晴天表现为顺时针时滞，而在阴天和雨天表现为逆时针时滞。另外，本研究也未考虑叶面积指数的变化对蒸腾量的影响。已有研究表明，同等辐射强度下，叶面积的大小决定着吸收能量的多少，因叶面积不同导致蒸腾存在差异^[46]，这均有可能影响本研究构建模型的模拟精度（74%），因此，未来还需继续考虑时滞效应与叶面积指数变化的影响，以提高模型模拟精度。

5. 结　　论

（1）林分蒸腾的日内变化呈现单峰或多峰的变化特征，蒸腾量的峰值（mm/h）表现为5月（0.173）> 6月（0.122）> 7月（0.916）> 8月（0.762）> 9月（0.468）。

（2）林分小时蒸腾量对R_s和VPD的响应均符合二次多项式函数，随R_s和VPD的增大，蒸腾量先增后减，达到最高值的R_s和VPD阈值分别为666.7 W/m²和1.86 kPa；而林分小时蒸腾对REW的响应符合趋于饱和的指数关系，随REW的增加，蒸腾量先增加，当REW大于0.3后逐渐趋于稳定。

（3）林分小时蒸腾可用耦合R_s、VPD和REW这3个因素影响的模型进行很好地预测和评估，模型为T = (− 6.347 0 × 10^{− 5} ${R_{\rm{s}}^2}$ − 0.637 0R_s − 208.734 8) × (− 0.003 2VPD² + 0.013 8VPD + 0.001 7) × (− 0.008 1 − 0.004 6(1 − exp(− 12.469 6REW)))。

图 1 林木空间利用率与胸径的关系

B_g、B_v、V_g、V_v是待定的林木空间利用率指标。B_g, B_v, V_g and V_v are the undetermined indexes of forest spatial utilization.

Figure 1. Relationship between forest space utilization and DBH

下载: 全尺寸图片幻灯片

图 2 各树种组线性模型拟合参数的95%置信区间

Figure 2. 95% confidence intervals on the linear model parameters for each tree species group

下载: 全尺寸图片幻灯片

图 3 整体预测（固定参数）、分组预测（树种组）与森林空间利用率观察值对比图

V_t是正态化后的林木空间利用率。V_t is normalization of forest space utilization.

Figure 3. Population predictions (fixed), within-group predictions (species group), and the observed forest space utilization versus DBH

下载: 全尺寸图片幻灯片

表 1 建模数据和检验数据主要指标统计信息

Table 1 Summary statistics for modeling and validation data sets

数据 Data	树种组 Tree species group	株树 Plant number	统计指标 Statistic index	胸径 DBH/cm	树高 Tree height/m	平均冠幅 Average crown width/m	样地蓄积/（m³·hm^{− 2}） Sample plot volume/ (m³·ha^{− 1})	针叶树比例 Conifer percentage
建模数据 Modeling data	红松 Pinus koraiensis	219	平均值 Mean	24.4	18.4	2.2	296.5	0.91
	红松 Pinus koraiensis	219	标准差 SD	8.4	3.9	0.7	73.7	0.06
	云杉 Picea koraiensis	271	平均值 Mean	22.1	17.9	2.1	288.3	0.88
	云杉 Picea koraiensis	271	标准差 SD	9.7	5.2	0.7	74.1	0.07
	冷杉 Abies holophylla	717	平均值 Mean	21.5	18.7	1.8	297.6	0.90
	冷杉 Abies holophylla	717	标准差 SD	7.9	4.4	0.6	76.9	0.06
	落叶松 Larix olgensis	80	平均值 Mean	22.0	20.7	2.2	263.6	0.90
	落叶松 Larix olgensis	80	标准差 SD	7.4	4.5	0.7	62.3	0.07
	中阔 Medium-speed broadleaf trees	57	平均值 Mean	19.5	19.7	2.0	333.0	0.87
	中阔 Medium-speed broadleaf trees	57	标准差 SD	6.6	4.5	0.9	53.2	0.05
	慢阔 Slow broadleaf trees	168	平均值 Mean	17.2	16.8	2.2	298.3	0.87
	慢阔 Slow broadleaf trees	168	标准差 SD	6.6	4.7	0.8	71.4	0.06
检验数据 Validation data	红松 Pinus koraiensis	122	平均值 Mean	24.2	18.9	2.1	294.5	0.91
	红松 Pinus koraiensis	122	标准差 SD	7.8	4.0	0.7	71.7	0.06
	云杉 Picea koraiensis	141	平均值 Mean	21.6	17.9	2.1	290.8	0.88
	云杉 Picea koraiensis	141	标准差 SD	8.6	5.0	0.7	76.0	0.07
	冷杉 Abies holophylla	357	平均值 Mean	22.8	19.3	1.9	305.4	0.90
	冷杉 Abies holophylla	357	标准差 SD	7.8	4.4	0.6	72.4	0.06
	落叶松 Larix olgensis	26	平均值 Mean	23.1	21.4	2.5	246.2	0.88
	落叶松 Larix olgensis	26	标准差 SD	6.7	3.9	0.8	51.4	0.08
	中阔 Medium-speed broadleaf trees	21	平均值 Mean	21.9	21.0	2.3	329.7	0.88
	中阔 Medium-speed broadleaf trees	21	标准差 SD	6.0	2.9	0.9	58.4	0.06
	慢阔 Slow broadleaf trees	89	平均值 Mean	17.0	17.0	2.2	297.7	0.86
	慢阔 Slow broadleaf trees	89	标准差 SD	6.5	4.6	0.8	78.7	0.06
注：SD为标准差。Note: SD means standard deviation.

下载: 导出CSV

表 2 林木空间利用率基础模型模拟结果

Table 2 Simulating results of basic model for forest space utilization

变量 Variable	估计值 Estimating value	方差 Variance	t	P (P_r > \|t\|)
截距 Intercept (INT)	− 2.767 04	0.019 55	− 141.542	< 0.000 1***
胸径 DBH	0.013 76	0.000 76	18.184	< 0.000 1***
胸径平方 Square of the DBH (DBH²)	− 0.000 18	0.000 01	− 13.335	< 0.000 1***
树高 Tree height (H)	0.001 26	0.000 35	3.553	0.000 39***
冠幅 Crown width (CW)	− 0.051 17	0.001 71	− 29.975	< 0.000 1***
蓄积 Stock volume (S)	− 0.000 14	0.000 01	− 9.249	< 0.000 1***
针阔比 Proportion of conifer to broadleaved trees (PF)	0.065 63	0.016 59	3.955	< 0.000 1***
坡度坡向 Slope degree and slope aspect (SLC)	0.001 36	0.000 42	3.245	0.001 19 **
竞争指数 Competition index (CIS)	− 0.005 58	0.000 94	− 5.928	< 0.000 1***
注：*表示在P < 0.001水平下差异显著，表示在P < 0.01水平下差异显著。Notes: * represents significant difference at P < 0.001 level, represents significant difference at P < 0.01 level.

下载: 导出CSV

表 3 不同随机效应拟合结果统计检验

Table 3 Goodness-of-fit statistics for mixed model of different random effects

模型编号 Model No.	随机参数 Random parameter	AIC	BIC	loglikelihood
VTLME1	INT	− 5 142.105	− 5 083.638	2 582.053
VTLME2	INT DBH	− 5 161.782	− 5 092.684	2 593.891
VTLME3	INT H	− 5 145.099	− 5 076.001	2 585.550
VTLME4	INT SLC	− 5 150.207	− 5 081.109	2 588.104
VTLME5	INT DBH²	− 5 165.259	− 5 096.161	2 595.630
VTLME6	INT DBH² SLC	− 5 172.721	− 5 087.678	2 602.360
注：VTLME1、VTLME2、VTLME3、VTLME4、VTLME5、VTLME6分别为加入相应随机参数的混合模型编号。Notes: VTLME1，VTLME2，VTLME3，VTLME4，VTLME5，VTLME6 are the mixed model codes with corresponding random parameters.

下载: 导出CSV

表 4 不同残差方差结构拟合结果统计检验

Table 4 Goodness-of-fit statistics for mixed model of different residual variance structure

模型编号 Model No.	残差方差模型 Residual variance model	AIC	BIC	loglikelihood
VTLME5	无 None	− 5 165.259	− 5 096.161	2 595.630
VTLME51	$\scriptstyle {\sigma }^{2}\mathrm{e}\mathrm{x}\mathrm{p}\left(2\gamma {\mathrm{D}\mathrm{B}\mathrm{H}}^{2}\right)$	− 5 167.432	− 5 093.019	2 597.716
VTLME52	$\scriptstyle {\sigma }^{2}\mathrm{e}\mathrm{x}\mathrm{p}\left(2\gamma \mathrm{C}\mathrm{W}\right)$	− 5 175.094	− 5 100.681	2 601.547
VTLME53	$\scriptstyle {\sigma }^{2}\mathrm{e}\mathrm{x}\mathrm{p}\left(2\gamma \mathrm{C}\mathrm{I}\mathrm{S}\right)$	− 5 174.558	− 5 100.145	2 601.279
VTLME54	$\scriptstyle {\sigma }^{2}\mathrm{e}\mathrm{x}\mathrm{p}\left(2\gamma f\right({x}_{i}\left)\right)$	− 5 185.268	− 5 110.855	2 606.634
VTLME55	$\scriptstyle {\sigma }^{2}{\mathrm{D}\mathrm{B}\mathrm{H} }^{2 \times2\gamma }$	− 5 170.525	− 5 096.112	2 599.263
VTLME56	$\scriptstyle {\sigma }^{2}{\mathrm{C}\mathrm{W}}^{2\gamma }$	− 5 175.849	− 5 101.436	2 601.925
VTLME57	$\scriptstyle {\sigma }^{2}{\mathrm{C}\mathrm{I}\mathrm{S}}^{2\gamma }$	不收敛 Not converge
VTLME58	$\scriptstyle {\sigma }^{2}{f\left({x}_{i}\right)}^{2\gamma }$	− 5 185.182	− 5 110.769	2 606.591
注：VTLME5、VTLME51、VTLME52、VTLME53、VTLME54、VTLME55、VTLME56、VTLME57、VTLME58分别为加入相应残差方差模型的混合模型编号； $\scriptstyle f\left({x}_{i}\right)$ 为固定效应及随机效应的预测值。Notes: VTLME5,VTLME51, VTLME52, VTLME53, VTLME54, VTLME55, VTLME56, VTLME57, VTLME58 are the mixed model codes with corresponding residual variance models; $\scriptstyle f\left({x}_{i}\right)$ represents the predicted value of the fixed effect and the random effect.

下载: 导出CSV

表 5 混合效应模型和基本线性模型拟合结果统计检验

Table 5 Goodness-of-fit statistics for mixed model and general linear model

项目 Item	建模数据 Modeling data		检验数据 Validation data
项目 Item	R_a²	RMSE	R_a²	RMSE
基础线性模型 General linear model	0.580	0.043	0.583	0.043
混合效应模型 Mixed effect model	0.599	0.042	0.598	0.042

下载: 导出CSV

参考文献(24)

[1]	亢新刚. 森林经理学[M]. 4版. 北京: 中国林业出版社, 2011: 152. Kang X G. Forest management[M]. 4th ed. Beijing: China Forestry Publishing House, 2011: 152.
[2]	方旭东. 异龄林林木成熟确定的方法[J]. 林业科学, 2007, 43(6):83−87. doi: 10.3321/j.issn:1001-7488.2007.06.015 Fang X D. Research of the confirmation method of mature level in uneven-aged forest[J]. Scientia Silvae Sinicae, 2007, 43(6): 83−87. doi: 10.3321/j.issn:1001-7488.2007.06.015
[3]	田猛. 天然异龄林主伐关键技术研究[D]. 北京: 北京林业大学, 2015. Tian M. The key technologies of the natural uneven-aged forest cutting[D]. Beijing: Beijing Forestry University, 2015.
[4]	Van Galen L G, Jordan G J, Musk R A, et al. Quantifying floristic and structural forest maturity: an attribute-based method for wet eucalypt forests[J]. Journal of Applied Ecology, 2018, 55(4): 1668−1681. doi: 10.1111/1365-2664.13133
[5]	陈亚南. 落叶松云冷杉林空间结构多样性及择伐模型的研究[D]. 北京: 北京林业大学, 2016. Chen Y N. Study on spatial structure diversity and selective cutting decision model of larch-sprue-fir stands[D]. Beijing: Beijing Forestry University, 2016.
[6]	惠刚盈, 赵中华, 胡艳波, 等. 我国西北主要天然林经营模式设计[J]. 林业科学研究, 2016, 29(2):155−161. doi: 10.3969/j.issn.1001-1498.2016.02.001 Hui G Y, Zhao Z H, Hu Y B, et al. Management models for natural forests in northwestern China[J]. Forest Research, 2016, 29(2): 155−161. doi: 10.3969/j.issn.1001-1498.2016.02.001
[7]	Gradel A, Ammer C, Ganbaatar B, et al. On the effect of thinning on tree growth and stand structure of white birch (Betula platyphylla Sukaczev) and Siberian larch (Larix sibirica Ledeb.) in Mongolia[J]. Forests, 2017, 8(4): 105. doi: 10.3390/f8040105
[8]	符利勇, 孙华. 基于混合效应模型的杉木单木冠幅预测模型[J]. 林业科学, 2013, 49(8):65−74. doi: 10.11707/j.1001-7488.20130810 Fu L Y, Sun H. Individual crown diameter prediction for Cunninghamia lanceolata forests based on mixed effects models[J]. Scientia Silvae Sinicae, 2013, 49(8): 65−74. doi: 10.11707/j.1001-7488.20130810
[9]	Lee S, Lee J, Kim S, et al. Forest structure and carbon dynamics of an intact lowland mixed dipterocarp forest in Brunei Darussalam[J]. Journal of Forestry Research, 2018, 29(1): 199−203. doi: 10.1007/s11676-017-0410-y
[10]	Arney J D. Tables for quantifying competitive stress on individual trees[R]. Victoria: Pacific Forestry Centre, 1973.
[11]	吕飞舟. 基于CSI的蒙古栎林木竞争与分级研究[D]. 长沙: 中南林业科技大学, 2016. Lü F Z. Study on the forest competition and classification of Quercus mongolica based on CSI[D]. Changsha: Central South University of Forestry & Technology, 2016.
[12]	张晔珵, 张怀清, 陈永富, 等. 基于树冠因子的林木竞争指数研究[J]. 林业科学研究, 2016, 29(1):80−84. doi: 10.3969/j.issn.1001-1498.2016.01.012 Zhang Y C, Zhang H Q, Chen Y F, et al. Study of tree competition index based on crown feature[J]. Forest Research, 2016, 29(1): 80−84. doi: 10.3969/j.issn.1001-1498.2016.01.012
[13]	刘强, 李凤日, 董利虎. 基于树冠竞争因子的落叶松人工林单木生长模型[J]. 植物研究, 2014, 34(4):547−553. doi: 10.7525/j.issn.1673-5102.2014.04.020 Liu Q, Li F R, Dong L H. Individual tree growth model of larch plantation based on crown competition factors[J]. Bulletin of Botanical Research, 2014, 34(4): 547−553. doi: 10.7525/j.issn.1673-5102.2014.04.020
[14]	臧颢, 雷相东, 张会儒, 等. 红松树高−胸径的非线性混合效应模型研究[J]. 北京林业大学学报, 2016, 38(6):8−16. Zang H, Lei X D, Zhang H R, et al. Nonlinear mixed-effects height-diameter model of Pinus koraiensis[J]. Journal of Beijing Forestry University, 2016, 38(6): 8−16.
[15]	孔雷. 金沟岭林场三种林型最优林分结构的研究[D]. 北京: 北京林业大学, 2013. Kong L. Optimal structures for three ecological forests in Jingouling Forest Farm[D]. Beijing: Beijing Forestry University, 2013.
[16]	雷相东, 李永慈, 向玮. 基于混合模型的单木断面积生长模型[J]. 林业科学, 2009, 45(1):74−80. doi: 10.3321/j.issn:1001-7488.2009.01.014 Lei X D, Li Y C, Xiang W. Individual basal area growth model using multi-level linear mixed model with repeated measures[J]. Scientia Silvae Sinicae, 2009, 45(1): 74−80. doi: 10.3321/j.issn:1001-7488.2009.01.014
[17]	辛营营, 韦新良, 王鑫. 利用均值类非完备型竞争指标分析林木竞争[J]. 西南林业大学学报, 2011, 31(4):29−34. doi: 10.3969/j.issn.2095-1914.2011.04.006 Xin Y Y, Wei X L, Wang X. Application of incomplete competition mean index to analysis of forest plant competition[J]. Journal of Southwest Forestry University, 2011, 31(4): 29−34. doi: 10.3969/j.issn.2095-1914.2011.04.006
[18]	赵俊卉. 长白山云冷杉混交林生长模型的研究[D]. 北京: 北京林业大学, 2010. Zhao J H. Growth modeling for spruce-fir forest in Changbai Mountains[D]. Beijing: Beijing Forestry University, 2010.
[19]	李春明. 基于两层次线性混合效应模型的杉木林单木胸径生长量模型[J]. 林业科学, 2012, 48(3):66−73. doi: 10.11707/j.1001-7488.20120311 Li C M. Individual tree diameter increment model for Chinese fir plantation based on two-level linear mixed effects models[J]. Scientia Silvae Sinicae, 2012, 48(3): 66−73. doi: 10.11707/j.1001-7488.20120311
[20]	孔雷, 亢新刚, 赵浩彦, 等. 长白山云冷杉针阔混交林最优竞争指标的研究[J]. 西北农林科技大学学报(自然科学版), 2014, 42(4):88−94, 101. Kong L, Kang X G, Zhao H Y, et al. Optimal competition indexes of spruce-fir conifer and broadleaf mixed stands in the Changbai Mountains[J]. Journal of Northwest A & F University (Natural Science Edition), 2014, 42(4): 88−94, 101.
[21]	Osborne J W. Improving your data transformations: applying the Box-Cox transformation[J]. Practical Assessment Research & Evaluation, 2010, 15(12): 1−9.
[22]	姜立春, 张锐, 李凤日. 基于线性混合模型的落叶松枝条长度和角度模型[J]. 林业科学, 2012, 48(5):53−60. doi: 10.11707/j.1001-7488.20120508 Jiang L C, Zhang R, Li F R. Modeling branch length and branch angle with linear mixed effects for Dahurian larch[J]. Scientia Silvae Sinicae, 2012, 48(5): 53−60. doi: 10.11707/j.1001-7488.20120508
[23]	Burnham K P, Anderson D R. Multimodel inference: understanding AIC and BIC in model selection[J]. Sociological Methods & Research, 2004, 33: 261−304.
[24]	Pinheiro J C, Bates D M. Mixed-effects models in S and S-plus[M]. New York: Springer-Verlag, 2000: 143.

施引文献(6)

期刊类型引用(3)

1.	蔡家珍. 闽南乡村低山河流型湿地公园植物群落构建. 漳州职业技术学院学报. 2024(04): 103-108 . 百度学术
2.	郭雅婷，李运远. 基于生物多样性的城市绿地植物群落构建途径. 风景园林. 2022(01): 59-63 . 百度学术
3.	杨土士，王伟文，常鸣，王雪梅. 北京市潜在风道的数值模拟与综合识别. 地球信息科学学报. 2020(10): 1996-2009 . 百度学术

其他类型引用(3)

资源附件(0)

图(3) / 表(5)

计量

文章访问数: 2649
HTML全文浏览量: 516
PDF下载量: 74
被引次数: 6

1. 研究区概况
2. 研究方法
2.1 气象条件监测
2.2 土壤水分监测
2.3 树干液流的测定与计算
2.4 林分蒸腾量的计算
2.5 数据处理
3. 结果与分析
3.1 环境因子的季节变化特征
3.2 树干液流速率及林分蒸腾的日内变化
3.3 林分小时蒸腾对单因素环境条件的响应
3.4 林分小时蒸腾对多因素的响应及耦合模型
4. 讨　　论
4.1 林分小时蒸腾对单因素环境条件的响应
4.2 多因素共同影响下的树木蒸腾
5. 结　　论

1. 研究区概况
2. 研究方法
2.1 气象条件监测
2.2 土壤水分监测
2.3 树干液流的测定与计算
2.4 林分蒸腾量的计算
2.5 数据处理
3. 结果与分析
3.1 环境因子的季节变化特征
3.2 树干液流速率及林分蒸腾的日内变化
3.3 林分小时蒸腾对单因素环境条件的响应
3.4 林分小时蒸腾对多因素的响应及耦合模型
4. 讨　　论
4.1 林分小时蒸腾对单因素环境条件的响应
4.2 多因素共同影响下的树木蒸腾
5. 结　　论

参考文献(24)

施引文献(6)

资源附件(0)

长白山云冷杉针阔混交林林木空间利用率混合模型

作者简介: 李杨，博士生。主要研究方向：天然林生长模型。Email：kitty.919@163.com 地址：100083 北京林业大学117信箱

责任作者: 亢新刚，教授，博士生导师。主要研究方向：天然林可持续经营。Email：xingangk@163.com 地址：同上

计量

出版历程