Determination of the average period of CH4 flux in a mixed plantation in Xiaolangdi Area of the Yellow River based on eddy covariance method
-
摘要:目的 随着涡度相关法长期连续观测CH4通量的研究在国际上日渐增加，准确计算CH4通量成为相关研究人员关注的热点问题之一。根据研究区实际情况，探究涡度相关数据在实际应用中适宜的采样频率和平均计算周期，为准确计算CH4通量提供理论依据。方法 采用不同的平均周期（15 ~ 720 min）对黄河小浪底人工混交林生态系统2016年7—8月CH4通量原始数据（采样频率10 Hz）进行计算，以30 min为准标准，比较不同平均周期计算的CH4通量日变化特征，分析不同平均周期对CH4通量计算的影响。结果 不同平均周期导致计算的CH4通量结果发生变化。15、60、120、240、360和720 min平均周期与30 min计算的CH4通量日变化特征趋势差异正午前后较大，而在早晨或傍晚差别较小；平均周期小于120 min时，其计算CH4通量日变化趋势与30 min一致，CH4的通量值随平均周期的增加而增大，当平均周期大于240 min，通量计算出现明显误差。结合Ogive函数计算分析，当平均周期小于15 min时，Ogive函数逐渐增大，当平均周期为60 min时，ogive函数逐渐平稳。结论 不同计算周期对CH4的计算结果有一定的影响，在本研究区下垫面情况下，计算月及其以上尺度的CH4通量采用60 min的平均周期，而研究日及其以下尺度的CH4通量变化特征时采用平均计算周期为15 min。Abstract:Objective The eddy covariance technique provides a useful tool to directly measure CH4 exchange between the vegetation and atmosphere. The eddy covariance data normally need to be regulated based on the actual situation of the study area for its application. An inappropriate average period can lead to the inaccurate estimation on CH4 flux. Therefore, some of the regulations were selected to obtain the suitable sampling frequency and average period.Method In this paper, the impact of average period on CH4 flux calculation had been analyzed in a mixed plantation in the Xiaolangdi Area of the Yellow River from July to August of 2016. CH4 flux was calculated in different average periods (15−720 min). CH4 flux obtained in different periods was analyzed, and the calculation of CH4 flux in different average periods was compared with that of 30 min average period. The influences of average period on the calculation of CH4 flux based on the original data (sampling frequency was 10 Hz) were examined. In addition, the Ogive function was applied to determine the low-frequency contribution to CH4 flux.Result The diurnal variations of CH4 flux were different in the average period of 15, 60, 120, 240, 360 and 720 min. Large differences occurred at noon and small differences occurred in the morning or evening. When the average period was shorter than 120 min, CH4 flux had same diurnal variation characteristics with 30 min value, and increased with the increase of the average period. The calculation of CH4 flux was estimated significantly inaccurately when the average period was longer than 240 min. The Ogive function increased when the averaging period was less than 15 min, and the Ogive function became gradually stable when the period was 60 min.Conclusion Different average periods have different influences in calculating CH4 flux. In this study, the optimal average period should be 60 min during the long-term observation, whereas the average period should be 15 min to obtain accurate CH4 flux at the daily time scale.
-
Keywords:
- eddy covariance method /
- CH4 flux /
- average period /
- mixed plantation
-
甲烷（CH4）是一种痕量温室气体，它所导致全球气候变暖的能力也是二氧化碳的28倍[1]，其快速增长趋势以及对全球生态环境和人类生存环境等造成潜在长期影响引起了各国政府和科学家的重视。森林生态系统是陆地生态系统的主体，甲烷通量很小[2-4]。目前全球CH4收支的评估存在较大不确定性，森林生态系统CH4通量估算不完整或估算偏差导致全球尺度下存在大约10 Tg/a的“丢失源”[5]。因此，准确测算森林生态系统冠层尺度CH4交换量，了解该生态系统吸收或释放CH4的源汇转换格局，是对CH4收支状况进行评估与预测的重要前提。涡度相关技术的不断发展，研发出高频响应的CH4浓度分析仪，因此长期、连续观测CH4通量的研究日渐增多。与此同时，基于涡度相关法观测CH4通量数据的可靠性和准确性也逐渐成为研究者首要关注的重点。
虽然涡度相关法被广泛应用[6-11]，其技术依然存在很多不确定性，包括仪器本身相关参数和野外安装过程中操作不规范[12-13]，采样的频率和平均计算周期不统一[14-15]，风速、温度以及其他物理量的谱特征在高、低频衰减[16]，密度订正[17]，平流订正[18-19]和坐标轴旋转[20-21]，夜间通量和重力波影响[12]等方面。理论上，采样频率越高，平均周期越长，其结果越靠近真值。但是平均周期太长，地表通量所包含的一些细节的变化过程可能会被遗漏，而平均周期太短，则会造成通量计算结果低估，相关通量研究人员普遍选择平均时间间隔在10 ~ 60 min内来计算通量平均值和气体数据[20, 22-23]，然而根据不同下垫面情况，可以采用较长平均时间[20, 24-26]。研究农田生态系统通量日变化特征时采用平均计算周期为10 min，而对其进行长期观测时则采用30 min平均计算周期更适合[27]。对于荒漠生态系统采用60 min更适合于长期通量观测，而对于通量日变化研究来说采用15 min更合适[28]。森林生态系统可能使用更长的平均时间（2 ~ 4 h），可以减少由于低频数据造成的影响[20, 27]。针对不同的研究内容，可以采用不同的研究周期。CH4通量在森林生态系统中含量相对较少，CO2通量的平均计算周期是否适用于CH4通量成为大家关注的内容。同时关于森林生态系统CH4通量观测的研究又鲜少报道，因此研究森林生态系统CH4通量计算的平均周期更是准确估算CH4通量的基础。
本文以华北南部低丘山地栓皮栎−侧柏−刺槐人工混交林生态系统为研究对象，利用涡度相关法观测CH4通量数据，研究不同平均周期对通量计算结果的影响，分析和确定在特定条件下合适的CH4通量平均计算周期阈值。
1. 研究地概况与研究方法
1.1 研究地区概况
本试验观测区域在河南省济源市国家林业局黄河小浪底森林生态定位研究站进行（35°01′N、112°28′E），该站处于太行山南麓，平均海拔高度为320 ~ 410 m。其气候类型属于暖温带大陆性季风气候。近30年来年平均气温13.4 ℃，全年日照时数为2 367.7 h。受季风气候影响，降水季节分配不均匀，主要集中在7、8、9月份，其7—9月降水量为438.0 mm，占全年的68.3%。这个地区季节性干旱特别是春季干旱严重，年蒸发量为1400 mm，无霜期220 ~ 230 d左右，植物生长期为210 ~ 220 d。统计全年风向主要以东北偏东、西南为主。该观测区域属于暖温带落叶阔叶林地带，树种以栓皮栎（Quercus variabilis）、侧柏（Platycladus orientalis）、刺槐（Robinia pseudoacacia）人工纯林及3个树种的针阔混交林为主，林龄分别为42、40和38年生，平均株高分别为10.5、8.2和9.3 m。林下植被多为酸枣（Ziziphus jujuba var. spinosa）、绿刚毛草（Celtwas bungeana）和中华苦荬菜（Ixeris chinensis），通量观测塔周围1.8 km2范围内林木覆盖率约为96%，平均郁闭度达0.7，平均坡度为14°，栓皮栎、侧柏、刺槐所占比例分别为80%、8%和12%，生长季植被叶面积指数（LAI）最大为6.3[29]。
1.2 涡度相关观测系统
开路式涡度相关系统主要由CSAT3型三维超声风速仪（Campbel Sci.Inc.，USA）和一个开放路径的快速响应红外CO2/H2O分析仪（LI-7500，Li-Cor.Inc.，USA）和红外CH4/H2O分析仪（LI-7700，Li-Cor.Inc.，USA）组成，安装高度均距离地面36 m，与CR5000数据采集器（Campbell Sci.Inc.，USA）相连，昼夜连续自动采集，原始数据采样频率为10 Hz，每30 min输出1组平均值。
1.3 平均周期确定的理论方法
Kaimal等[21]提出了估计平均周期的简单方法：
T=2σ2αταˉα2ε2 (1) 式中：
σα 为所研究时间序列α 的总体方差，τα 为积分时间尺度，ε为容许误差（ε=σˉα/ˉα ）。对于CO2/H2O通量计算来说，30 min的平均周期是个合理折中[20]。为了检验不同平均周期对通量计算结果的影响，选取平均周期分别是15、30、60、120、180、240和720 min。目前国际上通常采用30 min平均周期计算通量，本研究以平均计算周期30 min作为标准，比较并分析不同平均计算周期的CH4通量的差异。
1.4 涡度数据处理
本研究中，首先利用Eddypro 6.1软件（LI-COR，Lincoln，Nebraska，USA）对原始高频湍流数据（10 Hz）进行处理。包括以下步骤：提取数据，剔除异常值（含野点），时间延迟校正、坐标轴旋转、频率损失订正等必要的修正[30-34]。并对去除和缺失的数据进行插补。小于2 h的缺失数据选择线性内插法；采用平均日变化法（MDV）对大于2 h的缺失数据进行插补[35]。
1.5 平均周期确定的理论方法（Ogive函数）
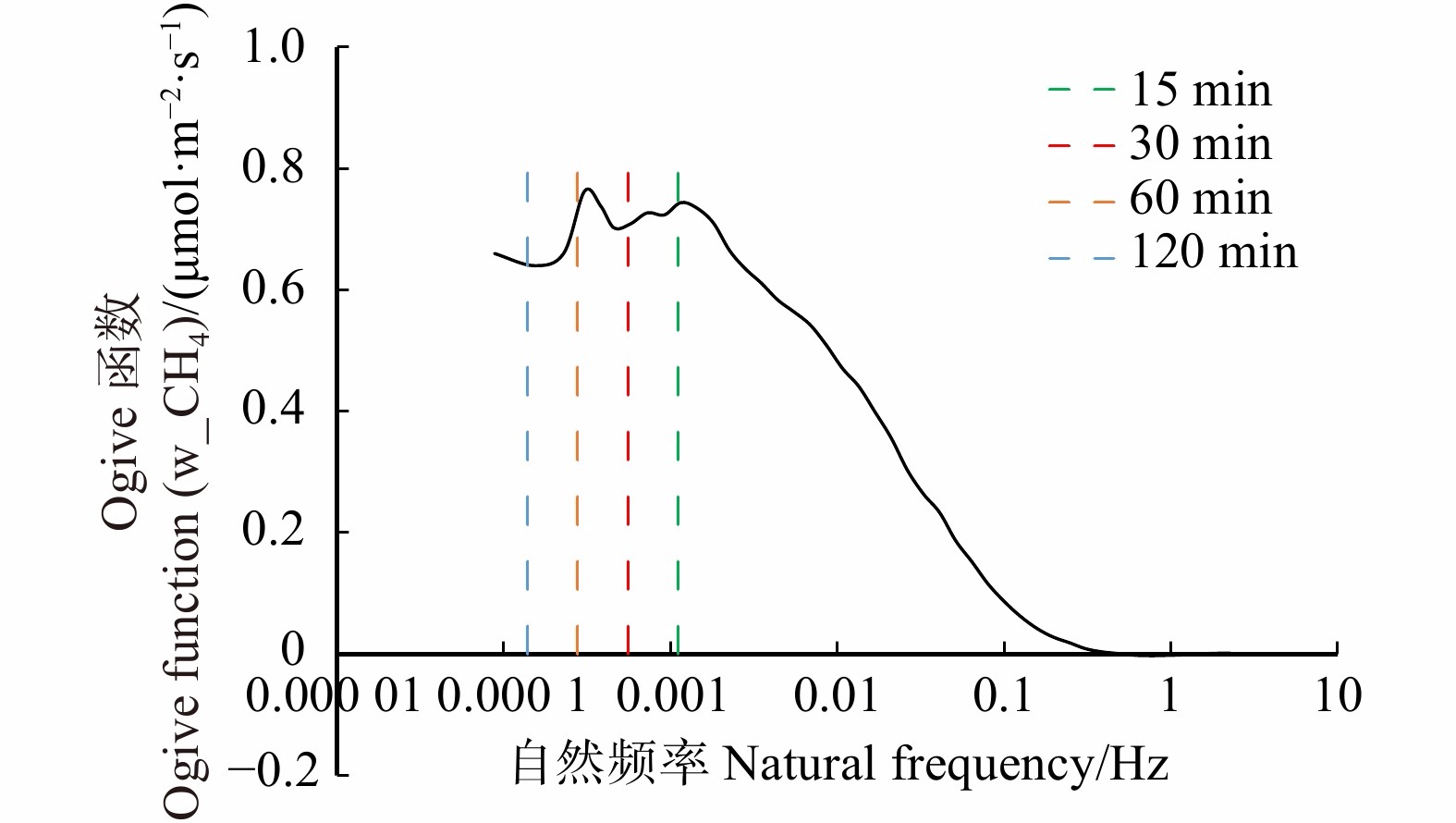
根据生态学和微气象学的相关原则，ChinaFLUX在采用涡度相关技术对植被−大气间CH4通量长期、连续观测时，需要确定合适计算数据的平均周期。要求其平均计算周期既可以清楚地分辨CH4通量的日变化特征，又可以识别短周期的极端情况对其通量变化的影响，同时还必须能捕捉大部分低频通量信息通过湍流谱特征分析。为了更准确的估算CH4通量的平均计算周期，许多相关科研工作者采用Ogive曲线即累计次数来确定合理的平均计算周期。Ogive函数是由协谱从高频到低频累计来表示[36]。平均周期对通量结果的影响分析可以通过频率分析来进行。Ogive函数表达为：
Ogwc(f)=∫ffhCowc(f)df (2) 式中：
fh 是尼奎斯特频率，取值为1/2的采样频率，f为频率；Cowc(f)表示为垂直风速和标量密度协谱。Ogive函数曲线从高频和低频方向延伸，并在某一低频处逐渐趋近于常数，此频率转化时间即为合适的通量计算周期。本研究选取常规晴天湍流强烈时间段（白天）涡度数据进行分析，计算每一段平均周期的Ogive曲线，以分析不同平均周期对CH4通量计算结果的影响。
2. 结果与分析
2.1 不同平均周期计算CH4通量日变化特征比较
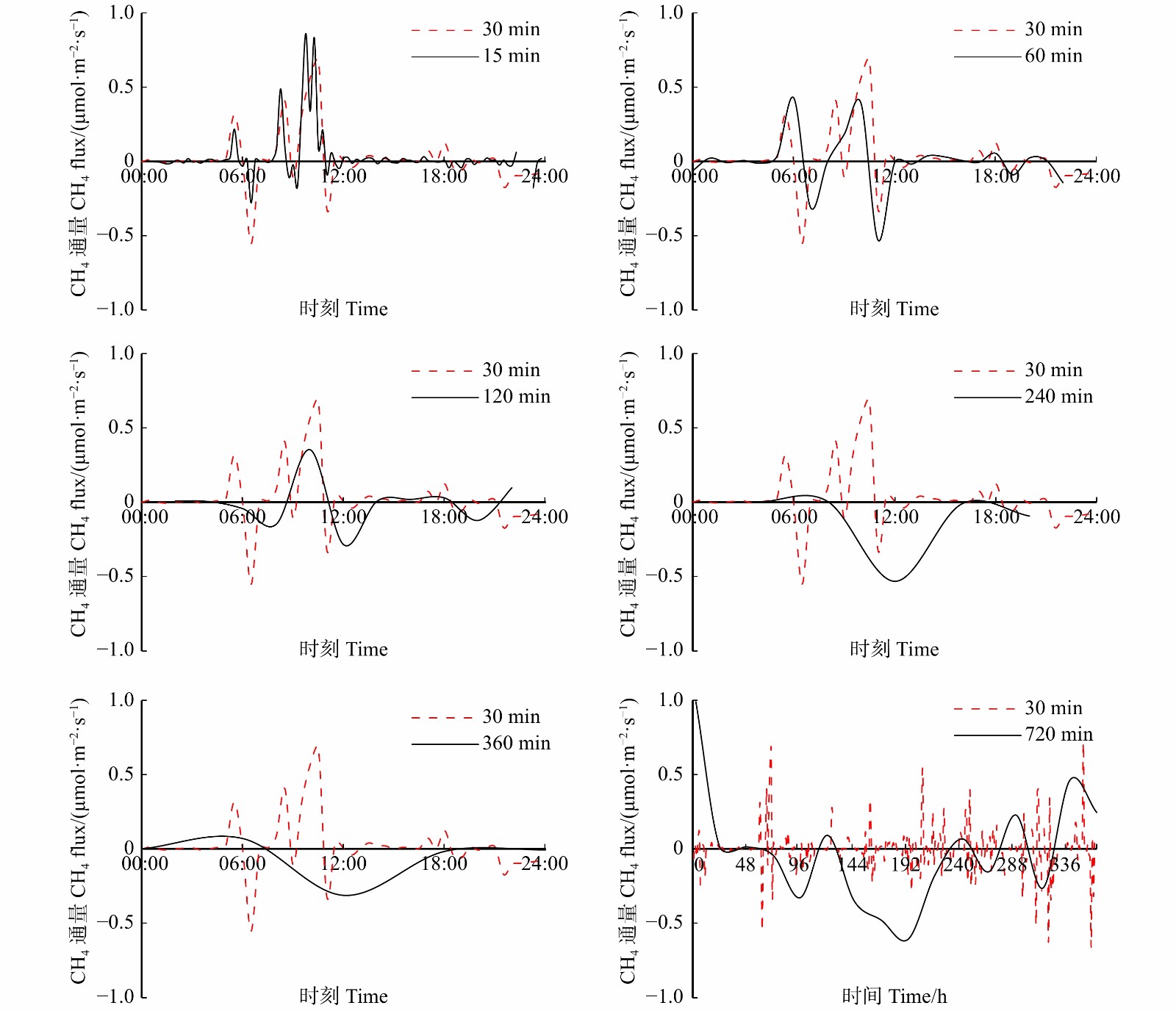
图1为典型晴天（2016年7月24日和7月24日至30日）15 ~ 720 min不同平均周期与30 min平均周期计算CH4通量的日变化特征比较。从图1中可以看出，以15 ~ 720 min不同平均周期计算的CH4通量没有明显的日变化特征，在06:00—12:00波动较大，在下午和夜间变化不明显。利用不同平均周期计算通量的差别在正午前后比较大，而在早晨或傍晚计算通量的差别比较小。以15、60和120 min为平均周期计算CH4通量结果与平均周期为30 min计算结果的日变化特征曲线形式基本保持不变。其中以15 min为平均周期计算CH4通量的结果与30 min计算结果的日变化特征最为一致，平均周期从15 min增大到120 min时，CH4通量的计算值逐渐增大，但是增幅较小。当平均周期大于120 min时，其计算CH4通量的日变化特征曲线与平均周期为30 min计算结果发生变异，计算的白天通量值日变化特征均出现相反趋势。这说明当平均计算周期超过120 min时，会影响通量计算值的稳定性。可能是由于太长的平均周期可能导致近地表层非定常条件的偏离，忽略短周期内的零星事件的影响，造成通量信息的缺失。夜间不同平均周期计算的通量值变化较小（如图1所示），通量强度小于白天，这说明不同平均周期对计算夜间通量值影响不大。而在白天正午前后都有比较大的差异，尤其是在平均周期大于120 min时，这可能受正午前后垂直风速物理量总体发生趋势变化的影响。
![]()
图 1 不同平均周期与30 min平均周期计算CH4通量的日变化特征（2016−07−24—2016−07−30）Figure 1. Diurnal variation characteristics of CH4 flux calculated by different average periods and 30 min average time ( July 24 to 30, 2016)表1为15 ~ 720 min不同平均周期与30 min平均周期计算通量结果比较。以30 min平均周期为准标准，分析不同平均周期（15 ~ 720 min）计算CH4通量与30 min平均周期计算通量之间的统计关系（如表1）。研究发现不同平均周期计算得到的CH4通量并不相同，CH4通量的计算值随着时间的增加而增大。随着平均计算周期的延长，低频信号获取较多，从而使得通量值增加。15 min平均周期比较短，计算的CH4通量值比30 min计算的值小，60和120 min计算得到的CH4通量值基本与30 min计算一致，而240 ~ 720 min时，平均周期过长，通量均值的绝对值都在一定程度上增大，且增大幅度呈现逐渐减小趋势。这说明，在120 min以内，延长平均周期计算的CH4通量值与平均周期为30 min计算结果相差不大，而平均周期大于30 min时，计算得出的CH4通量值不稳定。因此，超过120 min的平均周期对CH4通量计算可能是不适当的。
表 1 不同平均周期与30 min平均周期计算CH4通量之间的统计关系（2016−08）Table 1. Statistical relationship in calculating CH4 flux between different average periods (15−720 min) and 30 min average period (August, 2016)平均时间
Average time/min回归方程
Regression equationR2 15 y = 0.845x 0.967 30 y = x 1 60 y = 1.022x 0.899 120 y = 1.298x 0.812 240 y = 1.571x 0.94 360 y = 1.873x 0.871 720 y = 1.2433x 0.657 2.2 频谱相对贡献分析
平均周期对通量结果的影响分析可以通过频率分析来进行。通常采用Ogive函数在频率范围内把协谱从高频到低频进行累计，进而了解其在不同频率内的相对贡献[36]。由于大气稳定条件对湍流谱特征影响较大[37]，而夜间湍流较弱，不适合做Ogive频率信号的相对贡献分析，因此选取典型晴天2016年7月25日的10:00—14:00数据，对垂直风速与CH4的协谱积分进行累计，函数如图2所示，图中实线是Ogive函数曲线，虚线从左到右依次是15、30、60、120 min平均周期长度。图中结果显示，本研究区域在此观测高度下选取10 Hz的采样频率满足高频响应的要求。同时，随着平均周期的不断增加，Ogive函数逐渐上升，这表明在小于15 min的涡旋对通量计算的贡献较大。在15 ~ 60 min之内，变化不大，最大值出现在60 min，在60 ~ 120 min时，Ogive函数虽略微下降，但逐渐趋于平稳。由此可见，采用60 min平均计算周期较为合适。平均计算周期低于60 min，会低估湍流输送的低频涡旋；而平均周期大于60 min后，Ogive函数曲线发生小幅度下降波动，这说明大尺度的涡旋对于通量可能有负影响，这与表1的计算结果一致。因此为满足在提高数据时间分辨率的同时尽可能包括更多的通量信息，计算森林生态系统CH4通量的平均周期选取60 min较为合适，略长于CO2通量的平均计算周期。这是因为森林生态系统中，CH4通量比CO2通量小很多，低频信号贡献增大，从而需要更长的平均时间来捕捉较多的低频信号。
![]()
图 2 典型晴天（7月25日10:00—14:00 ）CH4通量的Ogive函数图Figure 2. Ogive function diagram for typical sunny daytime (25th July from 10:00 to 14:00)3. 讨 论
除仪器本身的相关参数外，采样频率和平均计算周期也是引起涡度相关法观测森林生态系统CH4通量不确定性之一。因此研究森林生态系统CH4通量平均计算周期是准确估算CH4通量的基础。基于通量变化特征和微气象的相关原则，理论上要求选择的平均周期尽可能的包含各种频率的湍流成分，即平均计算周期越长越好，不仅要可以分辨CH4通量的日变化特征，还必须能分辨短周期的零星事件的影响。因此本研究选择不同的平均周期计算CH4通量，探寻合适的平均计算周期。
不同平均周期计算出的CH4通量均没有明显日变化特征，但是利用不同平均周期计算通量的差别在正午前后比较大，而在早晨或傍晚计算通量的差别比较小，这可能是由于正午前后是湍流运动的旺盛时期，湍流运动剧烈。这与荒漠、农田生态系统研究结果一致[28, 38]。随着平均周期的增加，CH4通量逐渐增大，说明增加平均周期有通量值增大的倾向。以15 min为平均周期计算CH4通量的结果与30 min计算结果的日变化特征最为一致。平均周期从15 min增大到120 min时，CH4通量的计算值逐渐增大，但增幅较小；当平均时间高于120 min后，其计算结果与30 min平均时间计算白天通量值日变化特征均出现相反趋势。这说明当平均周期高于120 min时，对通量计算值的稳定度产生一定的影响。其可能的原因是过长的平均周期导致近地表层非定常条件的偏离，忽略短周期内的零星事件的影响，缺失部分通量信息。
合适的平均周期通常由假设大气处于稳态的Ogive函数来确定[39]。当Ogive函数曲线趋近于最大值或者最小值时，说明通量取值的范围都包含在此样本时段。平均时间少于15 min，Ogive值逐渐减小，由于损失低频部分的通量信息导致通量的计算值与真实值出现很大差距，而平均计算周期从15 min变化到120 min的过程中，Ogive曲线虽有波动，但波动不大，在60 min时候达到最大值，此时通量的计算值中低频部分未发生明显变化，而过长的平均计算周期（大于120 min）则会造成损失高频部分的通量信息。Kroon等[40]在CH4通量观测的不确定中提出，应采用大于30 min的平均周期可以计算更准确的CH4通量。本研究认为计算CH4通量的适宜平均周期为60 min，作日尺度及其以下尺度CH4通量变化特征时，为获得更多的通量信息合适的平均计算周期应选择15 min，研究结果与荒漠生态系统相一致[28]，比计算森林生态系统CO2通量的平均周期（30 min）略长[27, 41]。而农田生态系统相对于森林下垫面高度变化大，计算通量的平均周期大约在15 ~ 60 min之间[38, 42]。城市生态系统由于城市交通等源排放时间变异性大，合适的平均时间取30 min。过长的平均周期包含平流、膨胀和其他非湍流运动的贡献较大使通量计算结果产生较大误差[43]，最佳平均周期受下垫面、观测高度和地形等因素的影响较大，因此不同类型的下垫面选择合适的平均周期对准确计算CH4通量很重要。
4. 结 论
本研究利用黄河小浪底人工混交林的涡度相关系统观测的10 Hz原始数据，比较和分析不同平均周期对CH4通量计算结果的影响，结果发现选择不同平均周期对CH4通量计算值产生一定的影响。
通过分析15、60、120、240、360和720 min平均周期与平均周期为30 min计算的CH4通量日变化特征进行对比分析，发现正午前后差异比较大，而在早晨或傍晚计算通量的差别比较小。平均周期小于120 min时，其计算CH4通量日变化趋势与30 min计算结果一致，随着平均周期的增加，CH4的通量值增大，当平均周期大于240 min，通量计算出现明显误差。通过Ogive函数可以确定在本研究区环境下，CH4通量数据的平均计算周期为15 min和60 min，分别较适合于研究日尺度及其以下，月尺度及其以上尺度的CH4通量变化特征。
-
![]()
图 1 不同平均周期与30 min平均周期计算CH4通量的日变化特征（2016−07−24—2016−07−30）
Figure 1. Diurnal variation characteristics of CH4 flux calculated by different average periods and 30 min average time ( July 24 to 30, 2016)
![]()
图 2 典型晴天（7月25日10:00—14:00 ）CH4通量的Ogive函数图
Figure 2. Ogive function diagram for typical sunny daytime (25th July from 10:00 to 14:00)
表 1 不同平均周期与30 min平均周期计算CH4通量之间的统计关系（2016−08）
Table 1 Statistical relationship in calculating CH4 flux between different average periods (15−720 min) and 30 min average period (August, 2016)
平均时间
Average time/min回归方程
Regression equationR2 15 y = 0.845x 0.967 30 y = x 1 60 y = 1.022x 0.899 120 y = 1.298x 0.812 240 y = 1.571x 0.94 360 y = 1.873x 0.871 720 y = 1.2433x 0.657 
下载: 导出CSV
-
[1] IPCC. Climate change 2013: the physical science basic. contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change[C]. Cambridge: Cambridge University, 2013.
[2] 高升华, 张旭东, 汤玉喜, 等. 滩地人工林幼林不同时间尺度CH4通量变化特征: 基于涡度相关闭路系统的研究[J]. 生态学报, 2016, 36(18):5912−5921. Gao S H, Zhang X D, Tang Y X, et al. Dynamics and regulation of CH4 fluxes in a poplar plantation on a floodplain[J]. Acta Ecologica Sinica, 2016, 36(18): 5912−5921.
[3] Mikkelsen T N, Bruhn D, Ambus P, et al. Is methane released from the forest canopy?[J]. Iforest Biogeosciences and Forestry, 2011, 4(1): 200−204.
[4] Querino C A S, Smeets C J P P, Vigano I, et al. Methane flux, vertical gradient and mixing ratio measurements in a tropical forest[J]. Atmospheric Chemistry and Physics, 2011, 11(15): 7943−7953. doi: 10.5194/acp-11-7943-2011
[5] Megonigal J P, Guenther A B. Methane emissions from upland forest soils and vegetation[J]. Tree Physiology, 2008, 28: 491−498. doi: 10.1093/treephys/28.4.491
[6] 姚玉刚, 张一平, 于贵瑞, 等. 热带森林植被冠层CO2储存项的估算方法研究[J]. 北京林业大学学报, 2011, 33(1):23−29. Yao Y G, Zhang Y P, Yu G R, et al. Estimation of CO2 storage flux between forest and atmosphere in a tropical forest[J]. Journal of Beijing Forestry University, 2011, 33(1): 23−29.
[7] 郭晓楠, 查天山, 贾昕, 等. 典型沙生灌木生态系统凝结水量估算[J]. 北京林业大学学报, 2016, 38(10):80−87. Guo X N, Zha T S, Jia X, et al. Estimation of dewfall amount in a typical desert shrub ecosystem[J]. Journal of Beijing Forestry University, 2016, 38(10): 80−87.
[8] 母艳梅, 李俊, 同小娟, 等. 基于Penman-Monteith模型和Shuttleworth-Wallace模型对太行山南麓人工林蒸散的模拟[J]. 北京林业大学学报, 2017, 39(11):35−44. Mu Y M, Li J, Tong X J, et al. Evapotranspiration simulated by Penman-Monteith and Shuttleworth-Wallace models over a mixed plantation in the southern foot of the Taihang Mountain, northern China[J]. Journal of Beijing Forestry University, 2017, 39(11): 35−44.
[9] 王珊, 查天山, 贾昕, 等. 毛乌素沙地油蒿群落冠层导度及影响因素[J]. 北京林业大学学报, 2017, 39(3):65−73. Wang S, Zha T S, Jia X, et al. Temporal variation and controlling factors of canopy conductance in Artemisia ordosica community[J]. Journal of Beijing Forestry University, 2017, 39(3): 65−73.
[10] 李小梅, 张秋良. 环境因子对兴安落叶松林生态系统CO2通量的影响[J]. 北京林业大学学报, 2015, 37(8):31−39. Li X M, Zhang Q L. Impact of climate factors on CO2 flux characteristics in a Larix gmelinii forest ecosystem[J]. Journal of Beijing Forestry University, 2015, 37(8): 31−39.
[11] Baldocchi D D. How eddy covariance flux measurements have contributed to our understanding of global change biology[J]. Global Change Biology, 2019, 26(1): 1−19.
[12] Massman W J. A simple method for estimating frequency response corrections for eddy covariance systems[J]. Agricultural and Forest Meteorology, 2000, 104: 185−198. doi: 10.1016/S0168-1923(00)00164-7.
[13] Kristensen L, Mann J, Oncley S P, et al. How close is close enough when measuring scalar fluxes with displaced sensors[J]. Journal of Atmospheric and Oceanic Technology, 1996, 14(4): 814−821.
[14] Moore C J. Frequency response corrections for eddy correlation systems[J]. Boundary-Layer Meteorology, 1986, 37: 17−35. doi: 10.1007/BF00122754.
[15] Bosveld F C, Beljaars A C M. The impact of sampling rate on eddy-covariance flux estimates[J]. Agricultural and Forest Meteorology, 2001, 109: 39−45. doi: 10.1016/S0168-1923(01)00257-X.
[16] Lenschow D H, Raupach M R. The attenuation of fluctuations in scalar concentrations through sampling tubes[J]. Journal of Geophysical Research, 1991, 96(D8): 15259−15268. doi: 10.1029/91JD01437.
[17] Webb E K, Pearman G I, Leuning R. Correction of flux measurements for density effects due to heat and water vapor transfer[J]. Quarterly Journal of the Royal Meteorological Society, 1980, 106(447): 85−100. doi: 10.1002/qj.49710644707.
[18] Lee X. On micrometeorological observations of surface-air exchange over tall vegetation[J]. Agricultural and Forest Meteorology, 1998, 91: 39−49. doi: 10.1016/S0168-1923(98)00071-9.
[19] Schmid H P. Footprint modeling for vegetation atmosphere exchange studies: a review and perspective[J]. Agricultural and Forest Meteorology, 2002, 113: 159−183. doi: 10.1016/S0168-1923(02)00107-7.
[20] Finnigan J J, Clement R, Malhi Y, et al. A re-evaluation of long-term flux measurement techniques(Part I): averaging and coordinate rotation[J]. Boundary-Layer Meteorology, 2003, 107: 1−48. doi: 10.1023/A:1021554900225.
[21] Kaimal J C, Finnigan J J. Atmospheric boundary layer flows: their structure and measurement (Vii)[M]. New York: Oxford University Press, 1994: 255−261.
[22] Kristensen L, Fitzjarrald D R. The effect of line averaging on scalar flux measurements with a sonic anemometer near the surface[J]. Journal of Atmospheric and Oceanic Technology, 1984, 1(2): 138−146. doi: 10.1175/1520-0426(1984)001<0138:TEOLAO>2.0.CO;2
[23] Lenschow D H, Mann J, Kristensen L, et al. How long is long enough when measuring fluxes and other turbulence statistics[J]. Journal of Atmospheric and Oceanic Technology, 1994, 11: 661−673. doi: 10.1175/1520-0426(1994)011<0661:HLILEW>2.0.CO;2
[24] 王春林, 周国逸, 王旭, 等. 复杂地形条件下涡度相关法通量测定修正方法分析[J]. 中国农业气象, 2007, 28(3):233−240. Wang C L, Zhou G Y, Wang X, et al. Analysis of correction method on Eddy flux measurement over complex terrain[J]. Chinese Journal of Agrometeorology, 2007, 28(3): 233−240.
[25] Sakai R K, Fitzjarrald D R, Moore K E. Importance of low-frequency contribution to eddy fluxes observed over rough surfaces[J]. Journal of Applied Meteorology, 2001, 40: 2178−2190. doi: 10.1175/1520-0450(2001)040<2178:IOLFCT>2.0.CO;2.
[26] Moncrie J, Clement R, Finnigan J, et al. Handbook of micrometeorology[M]. London: Kluwer Academic Publishers, 2004: 7−31.
[27] 孙晓敏, 朱治林, 许金萍, 等. 涡度相关测定中平均周期参数的确定及其影响分析[J]. 中国科学D辑: 地球科学, 2004, 34(增刊2):30−36. Sun X M, Zhu Z L, Xu J P, et al. Determination of the averaging period of eddy covariance measurement and its influences on the calculation of fluxes[J]. Science in China Series D: Earth Sciences, 2004, 34(Suppl.2): 30−36.
[28] 张佩, 袁国富, 朱治林. 荒漠河岸林涡度相关通量测定中平均时间的确定及其对通量计算的影响[J]. 干旱区地理, 2013, 36(3):401−407. Zhang P, Yuan G F, Zhu Z L. Determination of the averaging period of eddy covariance measurement and its influences on the calculation of fluxes in desert riparian forest[J]. Arid Land Geography, 2013, 36(3): 401−407.
[29] Tong X J, Meng P, Zhang J S, et al. Ecosystem carbon exchange over a warm-temperate mixed plantation in the lithoid hilly area of the North China[J]. Atmospheric Environment, 2012, 49(3): 257−267.
[30] Vickers D, Mahrt L. Quality control and flux sampling problems for tower and aircraft data[J]. Journal of Atmospheric and Oceanic Technology, 1997, 14(3): 512−526. doi: 10.1175/1520-0426(1997)014<0512:QCAFSP>2.0.CO;2
[31] Wilczak J M, Oncley S P, Stage S A. Sonic anemometer tilt correction algorithms[J]. Boundary-Layer Meteorology, 2001, 99: 127−150. doi: 10.1023/A:1018966204465
[32] Ibrom A, Dellwik E, Larsen S E, et al. On the use of the Webb-Pearman-Leuning theory for closed-path eddy correlation measurements[J]. Tellus B: Chemical and Physical Meteorology, 2007, 59: 937−946. doi: 10.1111/j.1600-0889.2007.00311.x
[33] Ibrom A, Dellwik E, Flvbjerg H, et al. Strong low-pass filtering effects on water vapor flux measurements with closed-path eddy correlation system[J]. Agricultural and Forest Meteorology, 2007, 147: 140−156. doi: 10.1016/j.agrformet.2007.07.007
[34] Mauder M, Foken T. Documentaation and instruction manual of the eddy covariance software package TK2[Z]. Bayreuth: Bayreuth University, 2004: 1614−1616.
[35] Falge E, Baldocchi D, Olson R, et al. Gap filling strategies for defensible annual sums of net ecosystem exchange[J]. Agricultural and Forest Meteorology, 2001, 107(8): 43−69.
[36] Berger B W, Davis K J, Yi C, et al. Long-term carbon dioxide fluxes from a very tall tower in a northern forest: flux measurement methodology[J]. Atmospheric and Ocean Technology, 2001, 18: 529−542. doi: 10.1175/1520-0426(2001)018<0529:LTCDFF>2.0.CO;2.
[37] 倪攀, 金昌杰, 王安志, 等. 科尔沁草地不同大气稳定度下湍流特征谱分析[J]. 生态学杂志, 2009, 28(12):2495−2502. Ni P, Jin C J, Wang A Z, et al. Spectral analysis of turbulence characteristics under different atmospheric stablility regimes in Horqin grassland[J]. Chinese Journal of Ecology, 2009, 28(12): 2495−2502.
[38] 李佳, 陈岩, 秦淑静, 等. 涡度相关系统不同平均周期对干旱区玉米水热通量的影响[J]. 灌溉排水学报, 2018, 37(9):69−72. Li J, Chen Y, Qin S J, et al. Effects of different average periods in eddy covariance on calculation of heat and water fluxes in maize field in arid region[J]. Journal of Irrigation and Drainage, 2018, 37(9): 69−72.
[39] Foken T, Wichura B. Tools for quality assessment of surface-based flux measurements[J]. Agricultural and Forest Meteorology, 1996, 78(1/2): 83−105.
[40] Kroon P S, Hensen A, Jonker H J J, et al. Uncertainties in eddy covariance flux measurements assessed from CH4 and N2O observations[J]. Agricultural and Forest Meteorology, 2010, 150(6): 806−816.
[41] 吕少宁, 文军, 张宇, 等. 不同平均时间对LOPEX10资料涡动相关湍流通量计算结果影响的探讨[J]. 高原气象, 2012, 31(6):1530−1538. Lü S N, Wen J, Zhang Y, et al. Influence of the different averaging period on computing the turbulent fluxes using LOPEX10 data[J]. Plateau Meteorology, 2012, 31(6): 1530−1538.
[42] Feng J, Zhang B, Wei Z, et al. Effects of averaging period on energy fluxes and the energy-balance ratio as measured with an eddy-covariance system[J]. Boundary Layer Meteorology, 2017, 165(3): 545−551. doi: 10.1007/s10546-017-0284-8.
[43] 宋涛, 修天阳, 孙扬, 等. 城市复杂环境下涡度相关通量观测的适用性分析[J]. 环境科学学报, 2014, 34(5):1089−1098. Song T, Xiu T Y, Sun Y, et al. Applicability of eddy covariance technique to the measurement of turbulent fluxes in complex urban context[J]. Acta Scientiae Circumstantiae, 2014, 34(5): 1089−1098.
-
期刊类型引用(17)
1. 张禹，赵雯昊，乔沈启，王亚童，李会平，刘炳响. 不同针阔叶树蒸腾耗水特性及单位面积耗水量估算. 东北林业大学学报. 2025(01): 112-119 . 
百度学术
2. 杨安蓉，张超. 基于无人机遥感的云南松林冠参数提取研究. 西北林学院学报. 2024(01): 1-9 . 百度学术
3. 谢运鸿，孙钊，丁志丹，罗蜜，李芸，孙玉军. 基于Mask R-CNN和迁移学习的无人机遥感影像杉木单木树冠提取. 北京林业大学学报. 2024(03): 153-166 . 本站查看
4. 黄新峰，孙红召，冯东阳，李放，冯瑞琦，李伟，李丹. 应用小型无人机对毁坏林地开展调查分析. 河南林业科技. 2024(02): 25-28 . 百度学术
5. 孙钊，谢运鸿，王宝莹，谭军，王轶夫，孙玉军. 基于无人机多维数据集的森林地上生物量估测模型研究. 农业机械学报. 2024(06): 186-195+236 . 百度学术
6. 张振飞，郭靖，颜安，袁以琳，肖淑婷，侯正清，孙哲. 基于多光谱无人机不同飞行高度下苹果树冠幅信息的提取. 新疆农业科学. 2024(06): 1468-1476 . 百度学术
7. 穆喜云，李显玉，吴红雪，李秀华，张今奇，董文信，许成国. 无人机在不同飞行高度下的精度差异分析. 内蒙古林业调查设计. 2023(02): 86-88+38 . 百度学术
8. 杨晓慧，吴金卓，刘浩然，钟浩，林文树. 基于UAV-LiDAR的人工林林分郁闭度估测. 林业科学. 2023(08): 12-21 . 百度学术
9. 王娟，张超，陈巧，李华玉，彭希，白明雄，徐志扬，刘浩栋，陈永富. 结合无人机可见光和激光雷达数据的杉木树冠信息提取. 西南林业大学学报(自然科学). 2022(01): 133-141 . 百度学术
10. 周辰琴，余拥军，方陆明，刘雨真，胡建锦. 飞行高度与郁闭度对水杉冠幅提取影响的研究. 林业资源管理. 2022(01): 150-156 . 百度学术
11. 杨安蓉，张超，王娟，李华玉，白明雄，张玉薇. 应用无人机可见光遥感技术估测林分蓄积量. 东北林业大学学报. 2022(05): 70-75 . 百度学术
12. 李苏春，林露花，夏磊，胡璐璐，徐小军. 基于改进的局部最大值法提取杉木单木位置. 林业资源管理. 2022(05): 60-68 . 百度学术
13. 邬宁珊，王佳希，张岩，元慕田，张琪，高驰宇. 基于无人机可见光影像的树种和树冠信息提取——以晋西黄土区蔡家川流域为例. 浙江农业学报. 2021(08): 1505-1518 . 百度学术
14. 韩蕊，慕涛阳，赵伟，李丹. 基于无人机多光谱影像的柑橘树冠分割方法研究. 林业工程学报. 2021(05): 147-153 . 百度学术
15. 王瑞瑞，李怡燃，石伟，段芸杉，陈兴旺. 基于LiDAR和DOM数据的薇甘菊自动识别与分布预测. 农业机械学报. 2021(11): 263-270 . 百度学术
16. 姚慧芳，卢杰，王超，张萌. 基于混合效应法的急尖长苞冷杉林单木冠幅预测模型. 高原农业. 2021(06): 572-580 . 百度学术
17. 王娟，陈永富，陈巧，李华玉，张超. 基于无人机遥感的森林参数信息提取研究进展. 林业资源管理. 2020(05): 144-151 . 百度学术
其他类型引用(14)
计量
- 文章访问数: 1272
- HTML全文浏览量: 317
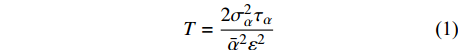
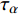
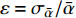
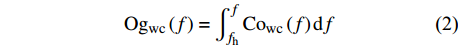
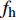
- PDF下载量: 58
- 被引次数: 31
