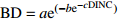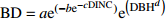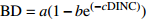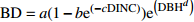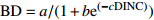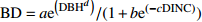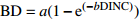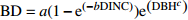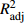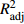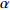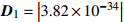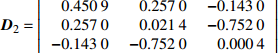基于混合效应的长白落叶松一级枝条基径预估模型

靳晓娟; 孙玉军; 潘磊

doi:10.12171/j.1000-1522.20200133

基于混合效应的长白落叶松一级枝条基径预估模型

北京林业大学森林资源和环境管理国家林业局重点实验室，北京 100083

基金项目: 国家自然科学基金项目（31870620）

详细信息

作者简介:
靳晓娟。主要研究方向：森林资源监测与模型模拟。Email：1072733074@qq.com　地址：100083 北京市海淀区清华东路 35 号北京林业大学林学院

责任作者:
孙玉军，教授，博士生导师。主要研究方向：森林资源监测与模型。Email：sunyj@bjfu.edu.cn　地址：同上

中图分类号: S757
计量
- 文章访问数: 1728
- HTML全文浏览量: 512
- PDF下载量: 115
出版历程
- 收稿日期: 2020-05-04
- 修回日期: 2020-07-06
- 网络出版日期: 2020-09-23
- 发布日期: 2020-10-24

Prediction model of base diameter of primary branch for Larix olgensis based on mixed effects

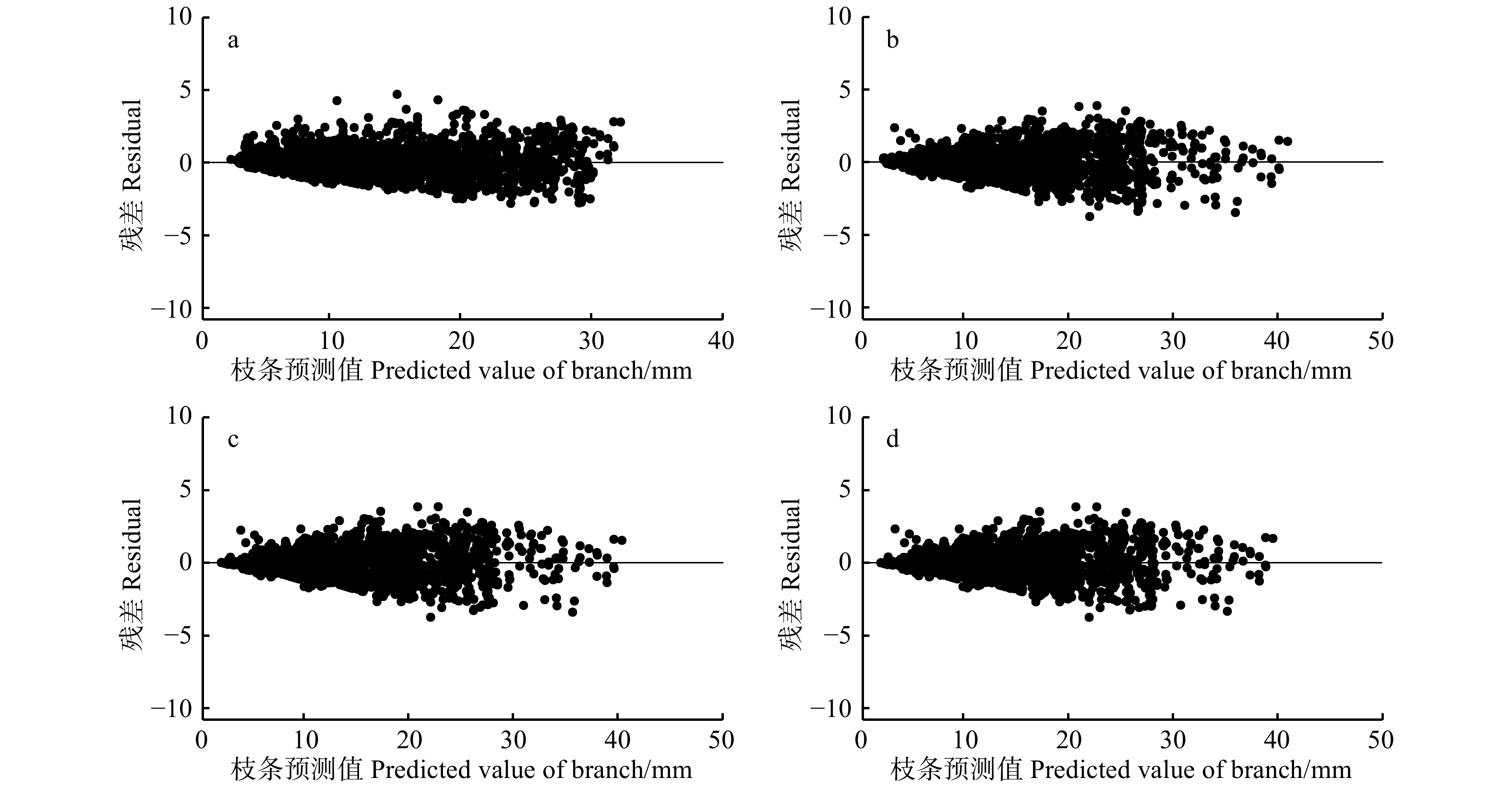
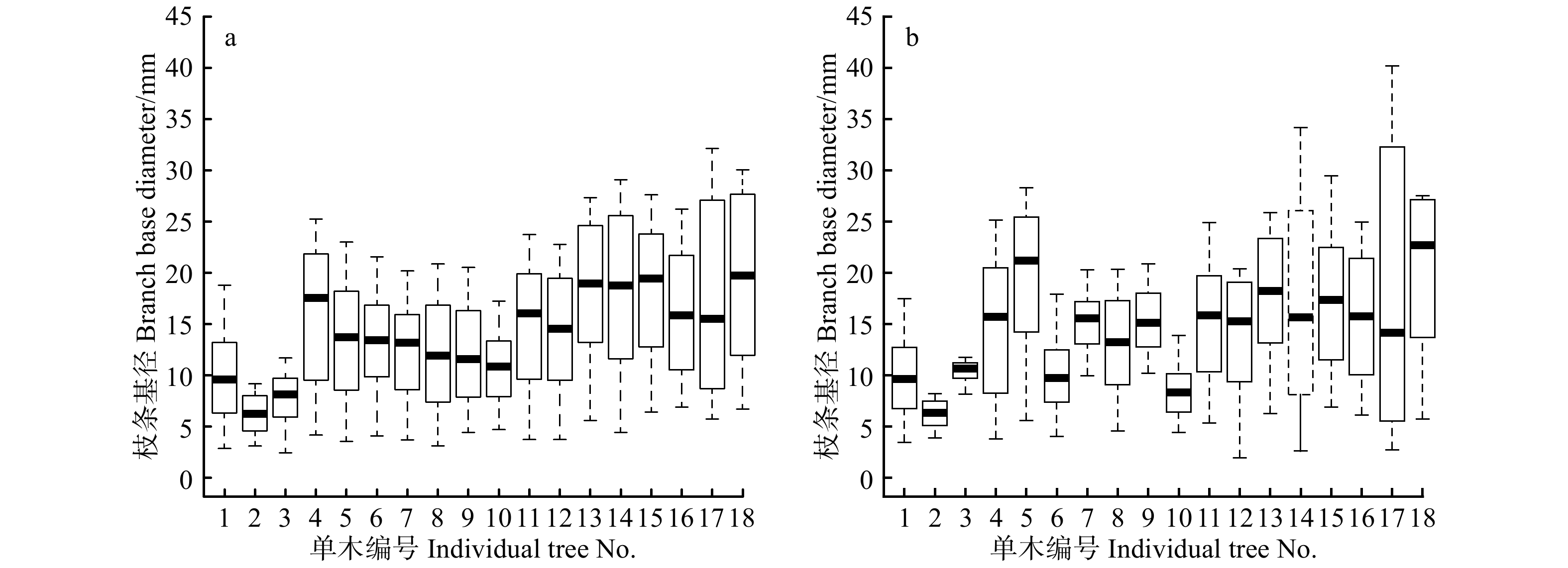
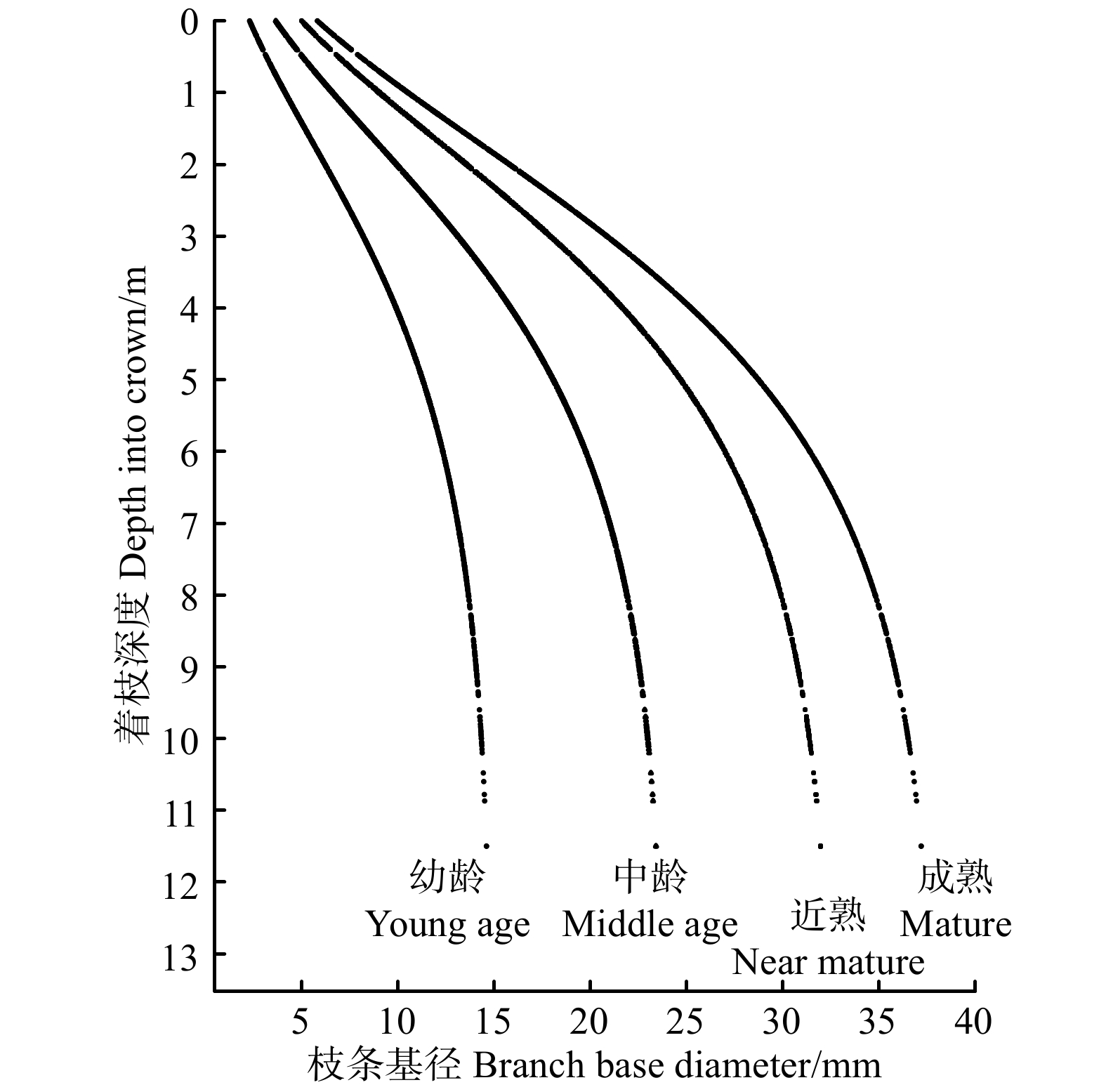
State Forestry Administration Key Laboratory of Forest Resources & EnvironmentalManagement, Beijing Forestry University, Beijing 100083, China

摘要

摘要:
目的利用非线性混合效应建模方法构建龄组−单木两水平长白落叶松一级枝条基径模型，为探索不同龄组下枝条基径的生长特点及差异提供理论依据。
方法对4个基础模型进行改进，通过调整系数（ $R_{\mathrm{a}\mathrm{d}\mathrm{j} }^{2}$ ），均方根误差（RMSE）选择备选模型，在此基础上构建长白落叶松枝条基径非线性混合效应模型。利用独立数据验证模型拟合结果，用平均绝对误差（MAE）、平均相对误差绝对值（MRAE）评价模型预测能力。并对基础模型与混合模型的预测值进行比较，利用龄组水平的随机参数模拟各龄组枝条基径的分布。
结果以改进后的Gompertz方程为基础模型，当龄组随机效应作用于参数b、单木随机效应同时作用于参数b、c、d上，随机效应的方差协方差结构为广义正定矩阵，异方差结构为幂函数时，模型的拟合效果最优。混合模型的 $R_{\mathrm{a}\mathrm{d}\mathrm{j} }^{2}$ 有所提升，RMSE、MAE和MRAE都明显降低。最终模型的 $R_{\mathrm{a}\mathrm{d}\mathrm{j} }^{2}$ 、RMSE、MAE和MRAE分别为0.699 8、4.768 4 mm、3.705 8 mm和0.391 6 mm。混合模型的预测值可体现单木间的差异，枝条基径的分布范围随着龄组的增大逐渐增大，各龄组的枝径生长均有差异。
结论考虑龄组与单木水平所构建的枝条基径混合效应模型能提高模型的预测精度。利用龄组水平的随机效应参数模拟枝条基径的生长可以反映其规律和差异，也符合树木生理学意义。因此基于龄组与单木两水平所构建的混合效应模型可对不同年龄长白落叶松一级枝枝条基径的生长进行合理的预测。
- 长白落叶松人工林 /
- 一级枝条基径 /
- 龄组 /
- 非线性混合效应模型
Abstract:
Objective This paper aims to establish an age group-individual tree two-level primary branch diameter model for Larix olgensis using the nonlinear mixed effect model approach, and provide theoretical basis for the research on the characteristics and differences of branch diameter growth in different age groups.
Method Out of four improved basic models, one was selected as the basic model after referring to the adjusting coefficient ( $R_{\mathrm{a}\mathrm{d}\mathrm{j} }^{2}$ ) and root mean square error (RMSE). Nonlinear mixed-effect model of the branch diameter was constructed based on the selected model. Independent data were used to verify the model fitting results, while mean absolute error (MAE) and mean relative absolute error (MRAE) were used to evaluate the model prediction ability. The prediction values of the basic model and the mixed model were compared. Simulation of the branch diameter distribution in each age group was done using the random parameters from age group level.
Result Based on the improved Gompertz equation, the model performed the best when the age group random effects acted on parameter b, the individual tree random effects acted on parameters b, c and d at the same time, the variance-covariance structure of the random effects was generalized positive definite matrix, and the heteroscedasticity structure was power function. The adjustment coefficient ( $R_{\mathrm{a}\mathrm{d}\mathrm{j} }^{2}$ ) of the mixed model was improved, and RMSE, MAE and MRAE were all significantly reduced. The values of the adjustment coefficient, RMSE, MAE and MRAE of the final model were 0.699 8, 4.768 4 mm, 3.705 8 mm and 0.391 6 mm, respectively. The predicted values of the mixed model reflected the differences between individual trees. The distribution range of branch diameter was found increasing with the increase of age groups, and the branch diameter growth showed difference between the age groups.
Conclusion The accuracy of the mixed effect model of branch diameter can be improved by incorporating the random effects of age groups and individual trees into the model. Simulation of the branch diameter growth using the random effect parameters in the age group level can reasonably reflect their growth patterns and differences, and also conform to the significance of the tree physiology. Therefore, the mixed effect model based on age group and individual tree level can reasonably predict the growth of primary branch diameter of Larix olgensis at different ages.
- Larix olgensis plantation /
- base diameter of primary branch /
- age group /
- nonlinear mixed effect model

HTML全文

热激蛋白（Hsp90）是一种在细菌、植物、动物中均广泛存在的高度保守的蛋白质分子^[1-2]，在ATP作用下，辅助参与细胞周期控制、激素信号传导和细胞凋亡等过程，是生物中一类非常重要的分子伴侣蛋白^[2-4]。Hsp90主要是以同型二聚体存在，具有3个结构域：高度保守的N端ATP结合结构域（NTD）、中间结构域（MD）和C端结构域（CTD）^[5]。Hsp90促进200多种蛋白质的正确构象和活化^[5-7]，是维持细胞稳态的重要蛋白^[8]。Hsp90的缺失会影响应激反应、生长发育以及胚胎发生等过程^[9]，对动物和植物的发育具有重要意义。对植物而言，胚胎不仅是植物体的基本形态，也是植物种子的重要组成部分^[10]。同时，胚胎也为人类生存提供了不可替代的物质基础。目前在拟南芥（Arabidopsis thaliana）等模式植物的研究中发现，Hsp90蛋白参与植物的胚胎发育。Samakovli等^[11]在对拟南芥的研究中发现：Hsp90蛋白与YDA信号通路成员之间的遗传互作会影响胚体和胚柄的发育，Hsp90s功能受损对其他基因的表达有影响，同时揭示了该基因在细胞命运决定和生长素分布中起重要作用。Luo等^[12]通过对拟南芥Hsp90家族成员进行研究，首次确定了AtHsp90.6为胚胎发生所必需的蛋白质，分析了AtHsp90.6与ATP或ADP结合的构象变化，进一步了解了Hsp90的作用机制。Lee等^[13]通过对红藻（Griffithsia japonica）雌雄配子体混合群体的cDNA文库进行差异筛选，发现Hsp90在雌配子体发育过程中表现活跃。由此可见，Hsp90在生殖发育过程中起着重要作用。

板栗（Castanea mollissima）原产中国，是著名的坚果树种。中国年产板栗坚果量占全球产量的80%以上，居世界首位，但单产较低^[14]。雌雄花比例失调、授粉受精不良和胚败育造成的结实率低是中国板栗低产的主要原因^[15]。受精且胚胎正常发育是保证板栗产量的关键环节，二者任一时期发生败育均会降低其结实率，从而严重影响产量^[16]。因此，研究板栗胚珠败育的机理，对提高板栗产量具有重要意义。

综上所述，Hsp90基因家族在模式植物中已经被鉴定与胚发育有关，但是在板栗胚珠发育过程中的作用机理目前尚不清楚。本研究利用生物信息学方法对板栗Hsp90基因家族进行鉴定，对其基因结构以及在授粉受精过程中胚珠中的表达情况进行分析，为进一步研究板栗Hsp90基因的功能，以及与胚珠发育、败育的关系提供理论基础。

1. 材料与方法

1.1 试验材料

试验材料取自河北省遵化市魏进河国家板栗良种繁育基地（117°45′11″E，40°21′22″N），试验母株为‘遵化短刺’（C. mollissima ‘Zunhuaduanci’），授粉品种为‘紫珀’（C. mollissima ‘Zibo’）和‘东陵明珠’（C. mollissima ‘Donglingmingzhu’），树龄10年。花期进行套袋不授粉和人工充分授粉处理，每种方式处理10株树，每株树选取50个总苞。套袋不授粉：6月3日用硫酸纸袋套住雌花簇以隔离花粉，当栗园雄花序散粉结束后取下纸袋；人工充分授粉：6月15日柱头分叉30° ~ 45°（最佳授粉期）进行人工辅助授粉，上午11点将刚采集的混合花粉用毛笔对套袋雌花簇点授，并于次日11点重复上述操作以确保授粉充分^[17-18]。

1.2 研究方法

1.2.1 Hsp90基因家族成员的鉴定

通过在线网站GigaDB（http://gigadb.org/dataset/view/id/100643）搜索并下载板栗的基因组蛋白序列及注释文件，通过TAIR网站（https://www.arabidopsis.org/）搜索并下载拟南芥的全基因组蛋白序列及基因注释文件，利用NCBI（https://www.ncbi.nlm.nih.gov/genome/）搜索并下载水稻（Oryza sativa）和毛果杨（Populus trichocarpa）的全基因组蛋白序列及注释文件。Hsp90（PF00183）隐马尔科夫模型（HMM）从Pfam网站（http://pfam.xfam.org/search#tabview=tab1）下载，并将其作为搜索模型，以E-value < 10⁻⁵为搜索标准，利用HMMER（V3.2.1）软件构建本地蛋白数据库进行搜索。为了使得到的Hsp90家族基因更加准确，通过TBtools软件^[17]中的双向blast比对功能，对Hsp90基因家族做进一步比对，得到所有家族基因成员，随后与基因组结果进行比对，得到Hsp90基因家族的所有成员。通过NCBI-CDD数据库（https://www.ncbi.nlm.nih.gov/Structure/bwrpsb/bwrpsb.cgi）和SMART网站（http://smart.embl-heidelberg.de/）对Hsp90蛋白结构域进行预测^[19]，剔除不含有Hsp90家族蛋白结构域的序列。利用在线网站ExPASy（https://web.expasy.org/compute_pi/）对Hsp90基因家族的理化性质进行分析。使用在线服务器SignalP 5.0（http://www.cbs.dtu.dk/services/SignalP/）预测Hsp90基因家族蛋白是否存在信号肽以及所在的位点。

1.2.2 Hsp90基因家族蛋白序列及结构分析

利用在线网站MEME（http://meme-suite.org/tools/meme）预测Hsp90蛋白序列的保守基序，motif的最大值设为15，构建基因家族成员的蛋白保守基序。利用TBtools可视化工具结合基因组注释文件对基因的结构进行可视化^[20]。利用WoLFPSORT网页在线工具（https://wolfpsort.hgc.jp/）预测板栗CmHsp90家族蛋白的亚细胞定位。

1.2.3 Hsp90基因家族启动子的顺式作用元件分析

利用TBtools工具提取Hsp90基因转录起始位点上游2 000 bp长度的序列作为其启动子区，并通过在线网站PlantCARE（http://bioinformatics.psb.ugent.be/webtools/plantcare/html/）对Hsp90启动子区的顺式作用元件进行预测和分析，最后利用TBtools工具进行启动子位置可视化分析。

1.2.4 Hsp90基因家族多序列比对与系统发育进化树构建

利用DNAMAN软件将板栗、拟南芥、毛果杨、水稻4个物种的Hsp90蛋白序列进行比对，并采用邻接法（neighbor-joining）构建系统进化树。利用在线网站iTOL（https://itol.embl.de/）对进化树进行美化，分析板栗Hsp90家族基因与其他物种Hsp90的进化关系。

1.2.5 Hsp90基因在胚珠不同发育时期的表达分析

本课题组在前期研究中基本确定板栗在授粉后18 d时胚珠已完成受精^[20]。以授粉后18 d为参考时间点，采集充分授粉后7 d（7SF）、15 d（15SF）、18 d（18SF）、21 d、27 d以及套袋未授粉（18WF，与18 d授粉胚珠同时采集）胚珠作为试验材料，7SF、15SF为授粉受精前胚珠，18SF、21 d、27 d为受精后胚珠，21、27 d胚珠又分为发育（21FY、27FY）与败育（21BY、27BY）胚珠。试验材料剥取后经液氮冷冻，放入−80 ℃超低温冰箱保存。

剥取的胚珠样品均装于1.5 mL冻存管中，每个样品进行3个重复，共24个样品。采集来的样品使用Omega公司（美国）Plant RNA试剂盒进行胚珠总RNA提取，并使用Thermo Scientific公司（美国）RapidOut DNA Removal试剂盒进行DNA消化，将提取的胚珠RNA样品进行纯度、浓度和完整度检测，操作步骤参考文献^[21]。随后委托北京百迈客生物科技有限公司（北京，中国）进行不同时期胚珠样品的cDNA文库构建和Illumina HiSeqTM 2000高通量双端测序，用HISAT2^[22]RNA测序实验reads的高效比对系统将板栗基因组（http://gigadb.org/dataset/100643）作为参考基因组进行序列比对，比对分析完成后利用StringTie^[23]对比对上的reads进行组装和定量分析。利用百迈客云平台（http://www.Biocloud.net/）从RNA-seq数据中提取CmHsp90家族成员的表达量，并利用Sigmaplot 12.5软件绘制表达图，对不同样品中Hsp90的表达情况进行分析。

2. 结果与分析

2.1 CmHsp90家族基因的鉴定

利用HMMER软件和双向blast比对最终确定了10个板栗Hsp90家族基因，分别命名为：CmHsp90-1 ~ CmHsp90-10（表1）。10个CmHsp90基因家族成员的编码区序列（CDS）长度范围是2 112 ~ 2 481 bp，含有4 ~ 22个外显子，编码的氨基酸数目范围是703 ~ 826，相对分子量范围是80.67 ~ 94.21 kDa，等电点pI范围介于4.81 ~ 5.26。不稳定系数介于36.15 ~ 46.75之间，除CmHsp90-4、CmHsp90-6、CmHsp90-9外，其他基因编码的蛋白相对比较稳定。利用WoLF PSORT网站对CmHsp90家族蛋白进行亚细胞定位预测，结果显示：有5个成员（CmHsp90-1、CmHsp90-4、CmHsp90-5、CmHsp90-9、CmHsp90-10）定位到了细胞质上，2个成员（CmHsp90-7、CmHsp90-8）定位到了内质网上，其余3个成员分别定位到细胞核（CmHsp90-3）、线粒体（CmHsp90-2）和叶绿体上（CmHsp90-6）（表1）。利用SignalP 5.0对该基因家族的氨基酸序列进行信号肽预测，发现除CmHsp90-7和CmHsp90-8存在潜在的信号肽位点外，其余成员均不含有信号肽（图1）。

表 1 板栗CmHsp90基因家族信息

Table 1. Information of CmHsp90 gene family in Castanea mollissima

基因名称 Gene name	基因ID Gene ID	亚细胞定位 Subcellular localization	编码区长度 CDS length/bp	外显子数目 Exon numbert	编码蛋白质特性 Characteristic of the coding protein
基因名称 Gene name	基因ID Gene ID	亚细胞定位 Subcellular localization	编码区长度 CDS length/bp	外显子数目 Exon numbert	氨基酸长度 Amino acid length/aa	不稳定性系数 Instability coefficient	分子质量 Molecular mass/kDa	等电点 Isoelectric point
CmHsp90-1	BUA.CMHBY201654	细胞质 Cytosol	2 118	4	705	39.04	81.22	5.03
CmHsp90-2	BUA.CMHBY202913	线粒体 Mitochondrion	2 415	22	804	36.97	91.02	5.26
CmHsp90-3	BUA.CMHBY204630	细胞核 Nucleus	2 127	3	708	38.93	81.11	4.94
CmHsp90-4	BUA.CMHBY213842	细胞质 Cytosol	2 112	4	703	40.96	80.74	4.97
CmHsp90-5	BUA.CMHBY214124	细胞质 Cytosol	2 118	3	705	39.89	80.67	4.97
CmHsp90-6	BUA.CMHBY216742	叶绿体 Chloroplast	2 406	19	801	46.75	91.45	4.99
CmHsp90-7	BUA.CMHBY217539	内质网 Endoplasmic reticulum	2 481	14	826	36.38	94.21	4.87
CmHsp90-8	BUA.CMHBY217715	内质网 Endoplasmic reticulum	2 358	15	785	36.15	89.42	4.81
CmHsp90-9	BUA.CMHBY217794	细胞质 Cytosol	2 115	4	704	40.28	80.97	4.95
CmHsp90-10	BUA.CMHBY229404	细胞质 Cytosol	2 112	4	703	37.98	80.72	5.05

下载: 导出CSV

| 显示表格

图 1 CmHsp90家族蛋白序列的信号肽位点预测

SP（Sec/SPI）. 由Sec转座子转运并被信号肽酶I裂解的“标准”分泌信号肽；CS. 裂解位点；OTHER. 序列没有任何信号肽。SP(Sec/SPI), ‘standard’ secretory signal peptides transported by the Sec translocon and cleaved by signal peptidase I; CS, the cleavage site; OTHER, no signal peptide at all.

Figure 1. Prediction of signal peptide sites in CmHsp90 family protein sequence

下载: 全尺寸图片幻灯片

2.2 CmHsp90基因家族蛋白的结构分析

利用DNAMAN软件对板栗CmHsp90基因家族成员的氨基酸序列进行同源多序列比对发现：CmHsp90基因家族蛋白的序列相似性为64.12%，均含有HATPase_c和Hsp90 superfamily保守结构域，说明CmHsp90家族蛋白在结构和组成上具有保守性（图2）。利用在线MEME软件对CmHsp90蛋白的motif进行分析，共鉴定到15个motif（图3）。CmHsp90-1、CmHsp90-3、CmHsp90-4、CmHsp90-5、CmHsp90-9、CmHsp90-10中包含所有15个motif，CmHsp90-2、CmHsp90-6、CmHsp90-7、CmHsp90-8均不含motif14，CmHsp90-6除不含有motif14外，还不含有motif11；CmHsp90-8不含有motif12、13、14。对CmHsp90蛋白结构进行预测，结果发现，10个CmHsp90家族蛋白成员均包含Hsp90蛋白保守的Hsp90 superfamily、HtpG superfamily、HATPase_c、PTZ00272 superfamily结构域（图4）。总之，10个CmHsp90蛋白的motif在顺序及组成上基本一致，均包含了Hsp90蛋白的保守结构域，表明了Hsp90家族蛋白在板栗中具有高度的保守性（图3、图4）。

图 2 CmHsp90家族氨基酸多序列比对

Figure 2. Amino acid multiple sequence alignment of CmHsp90 gene family

下载: 全尺寸图片幻灯片

图 3 CmHsp90家族蛋白基序预测分析

Figure 3. Motif prediction and analysis of CmHsp90 family protein

下载: 全尺寸图片幻灯片

图 4 板栗CmHsp90蛋白功能域预测

Figure 4. Functional domain prediction of CmHsp90 protein in C. mollissima

下载: 全尺寸图片幻灯片

2.3 CmHSP90基因家族的顺式作用元件预测

本研究通过在线网站PlantCARE对板栗CmHsp90基因家族的启动子顺式作用元件进行了预测分析，结果发现，CmHsp90基因家族启动子上主要包含激素调控、逆境胁迫及光响应等相关顺式作用元件（图5）。与光响应相关的顺式作用元件在10个CmHsp90家族成员中均有预测到，且数量最多，这表明了CmHsp90基因可能参与植物光响应的相关调控；其次为ABA响应元件（Hsp90-10除外）及厌氧诱导元件（Hsp90-2除外）。值得注意的是：Hsp90-3和Hsp90-6基因启动子包含干旱响应元件，推测这2个基因在干旱胁迫中起重要作用；同时Hsp90-1、Hsp90-5、Hsp90-7、Hsp90-8含有低温响应元件，推测这4个基因可能与温度调控有关；Hsp90-2、Hsp90-4、Hsp90-7、Hsp90-8、Hsp90-9含有茉莉酸甲酯响应元件，其中Hsp90-2、Hsp90-7、Hsp90-8还含有玉米醇溶蛋白代谢调节元件。这些结果表明，CmHsp90基因家族成员可能在光响应、逆境胁迫、激素响应等通路中发挥着重要的作用。

图 5 板栗CmHsp90家族基因启动子顺式作用元件预测分析

Figure 5. Functions of promoter cis-acting elements in CmHsp90 family genes in C. mollissima

下载: 全尺寸图片幻灯片

2.4 CmHsp90基因家族系统进化分析

为了进一步确定板栗CmHsp90基因家族的功能及特点，我们利用10个板栗、7个拟南芥、8个水稻、10个毛果杨Hsp90蛋白序列构建系统进化树（图6）。参考拟南芥^[24-25]、水稻^[26]、毛果杨^[27]Hsp90基因家族中的分组依据，35个Hsp90蛋白可以分为5组（Ⅰ ~ Ⅴ），5个分组中分别含有4、5、6、8、12个基因，且每个分组中均有板栗CmHsp90家族蛋白分布。其中，Ⅳ组中含有板栗CmHsp90家族成员最多，包括CmHsp90-1、CmHsp90-4、CmHsp90-9、CmHsp90-10；Ⅰ组和Ⅴ组均含有2个Hsp90蛋白，分别为CmHsp90-7、CmHsp90-8和CmHsp90-3、CmHsp90-5；Ⅱ组和Ⅲ组均含有1个蛋白，分别为CmHsp90-2和CmHsp90-6。聚为一组的蛋白具有较高的同源性，在功能上可能存在共性，因此，可参考其他物种Hsp90的研究结果对板栗CmHsp90基因家族的功能做出初步判断。

图 6 Hsp90家族蛋白进化树

Figure 6. Unrooted phylogenetic tree of Hsp90 gene family

下载: 全尺寸图片幻灯片

2.5 CmHsp90基因家族成员在胚发育过程中的表达分析

已有研究表明：Hsp90基因家族参与植物胚胎的发育，在植物胚形成和发育过程中发挥着重要的作用。因此，为了确定板栗CmHsp90基因家族成员是否参与板栗胚发育过程，我们利用转录组测序技术对板栗CmHsp90基因家族成员在胚发育不同时期的表达进行了分析（图7）。结果发现：除CmHsp90-3外，其他CmHsp90基因在受精前胚珠中的表达量均高于受精后胚珠，说明板栗CmHsp90基因可能在早期雌配子体发育过程中发挥重要作用。对授粉后18 d胚珠及未授粉胚珠中CmHsp90基因的表达量进行分析（图8），发现除CmHsp90-3在授粉胚珠中的表达量高于未授粉胚珠外，其余CmHsp90基因均低于未授粉胚珠，说明CmHsp90基因可能参与调控板栗的受精过程。对授粉后同一时期发育胚珠与败育胚珠中CmHsp90基因的表达情况做进一步分析（图9），结果显示：CmHsp90-2、CmHsp90-4、CmHsp90-5、CmHsp90-7、CmHsp90-8、CmHsp90-9、CmHsp90-10基因在发育胚珠中的表达量高于败育胚珠，其中，CmHsp90-4和CmHsp90-9、CmHsp90-10的差异最明显，说明这些基因可能正调控受精后胚珠的发育。

图 7 CmHsp90基因在胚珠不同发育时期的表达分析

7SF. 授粉后7d；15SF. 授粉后15 d；18SF. 授粉后18 d；21FY. 授粉后27 d发育胚珠；27FY. 授粉后27 d发育胚珠。下同。7SF, 7 days after pollination; 15SF, 7 days after pollination; 18SF, 18 days after pollination; 21FY, ovule developed 27 days after pollination; 27FY, ovule developed 27 days after pollination. The same below.

Figure 7. Expression analysis of CmHsp90 gene family in different development stages of ovule

下载: 全尺寸图片幻灯片

图 8 CmHsp90基因在授粉后18 d和未授粉胚珠中的表达情况

18WF. 未授粉，与18 d授粉胚珠（18SF）同时采集。18WF, unpollinated, collected at the same time with 18 day pollinated ovules (18SF).

Figure 8. Expression of CmHsp90 gene in 18 days after pollination and unpollinated ovules

下载: 全尺寸图片幻灯片

图 9 CmHsp90基因在发育胚珠与败育胚珠中的表达情况

21BY. 授粉后21 d败育胚珠；27BY. 授粉后27 d败育胚珠。21BY, ovule aborted 21 days after pollination; 27BY, ovule aborted 27 days after pollination.

Figure 9. Expression of CmHsp90 gene in ovule of pollination development and pollination abortion

下载: 全尺寸图片幻灯片

3. 讨　　论

目前，Hsp90基因家族在多种植物中已被鉴定^[24-27]，但板栗中Hsp90基因家族的信息尚不清楚。本研究利用多种生物信息学方法在板栗基因组中共鉴定到10个Hsp90家族基因。通过对10个CmHsp90基因家族蛋白序列的motif和蛋白结构域进行分析，发现该家族的蛋白具有很高的同源性，达64.12%。蛋白结构除全部匹配到Hsp90 superfamily外，还匹配到HATPase_c结构域。Hsp90 superfamily结构域和HATPase_c结构域是Hsp90蛋白的保守结构域，对Hsp90蛋白行使功能具有至关重要的作用。杜志如^[28]研究发现：水稻中Hsp90蛋白的HATPase_c结构域能与ATP相结合，同时还与CPS结合，共同作用合成氨甲酰磷酸，与水稻的抗性相关。将鉴定到的10个板栗CmHsp90蛋白与拟南芥、水稻、毛果杨Hsp90蛋白构建进化树，35个Hsp90蛋白被分为5个组，聚为一组的基因具有相似的蛋白结构和亚细胞定位结果^[24-27]，表明它们之间亲缘关系较近。目前，对模式植物拟南芥、水稻以及木本植物毛果杨的Hsp90基因家族研究较多，可参考拟南芥、水稻以及毛果杨Hsp90基因的研究结果预判同源关系较近的板栗CmHsp90的基因功能^[24-27]。

随后我们对CmHsp90家族基因的启动子进行顺式作用元件预测，发现所有CmHsp90基因启动子上均预测到了光响应元件。Feng等^[29]研究发现AtHsp90-5突变会导致拟南芥的叶绿体发育被抑制，胚胎发生缺陷；在对毛果杨Hsp90基因家族的研究中发现，定位到叶绿体上的PtHsp90-5a和PtHsp90-5b基因主要在幼叶和成熟叶中表达^[24]，因此推测板栗CmHsp90家族基因可能也与叶绿体相关。除预测到大量光响应元件外，还预测到了与逆境和激素相关的元件，说明CmHsp90基因参与了不同非生物胁迫的调控，这与早先Panaretou等^[30]的研究结果一致。目前，对热激蛋白的研究大部分都集中在其对温度胁迫的响应上，如对白菜（Brassica pekinensis）^[31]、拟南芥^[27]、番茄（Lycopersicon esculentum）^[32]和烟草（Nicotiana tabacum）^[33]等物种的研究，均说明Hsp90有助于提高植物的耐热性，但也有研究证明热激蛋白能提高植物抵抗冷胁迫的能力^[34-36]。Prasinos等^[37]研究发现：当胚胎组织受到热激时，胚胎中高度特异性的AtHsp90-1和AtHsp90-3的启动子驱动的基因表达发生了数量和质量上的变化，说明Hsp90基因参与了胚珠发育过程中对温度的响应过程。

我国板栗的单产相对较低，造成这一现象的原因与授粉受精不良和胚败育等密切相关^[1]。为了研究影响板栗授粉受精及胚珠发育的原因，我们采集了授粉与不授粉、授粉后不同发育阶段的胚珠，进行转录组测序并分析了CmHsp90基因家族在胚胎发育的不同时期的表达情况。通过对转录组数据进行分析发现：除CmHsp90-3外，其他CmHsp90基因在受精前后胚珠中的表达量变化较大，受精前胚珠中的表达量均高于受精后胚珠中的表达量，说明这些基因可能参与了板栗早期胚珠发育相关途径的调控。Sangster等^[38]通过抑制拟南芥Hsp90的表达发现：抑制表达的转基因植株其开花时间显著晚于对照，说明Hsp90基因可能与花器官的形成相关，这暗示了CmHsp90基因可能也参与板栗花器官的发育。Luo等^[12]在对拟南芥的研究发现：AtHsp90.6功能丧失可能导致胚胎致死，而拟南芥中AtHsp90.6基因与板栗中的CmHsp90-2聚为一类，同属于Ⅱ组，且都定位于线粒体，说明这2个基因的同源性较高，推测CmHsp90-2可能参与板栗的胚珠发育的调控。对授粉后21和27 d同一子房中发育和败育胚珠的转录组数据进行分析，发现发育胚珠中CmHsp90-2的表达量均高于败育胚珠，进一步说明该基因可能与胚珠发育相关。研究发现拟南芥中AtHsp90-1的启动子活性在胚胎发育的整个早期阶段普遍较低，但在胚胎成熟前变高，在子叶中表达最为突出^[37]，而与AtHsp90-1聚为一组的CmHsp90-1、CmHsp90-4、CmHsp90-9、CmHsp90-10，以及同样定位在胞质中的CmHsp90-5在授粉后21 d的表达量均低于授粉后27 d，即胚珠发育前期的表达量低于胚珠发育后期，与Prasinos等^[37]的研究结果基本一致，推测板栗中的这5个基因可能具有与AtHsp90-1基因相同的功能，可在后期实验加以验证。CmHsp90基因家族的功能在很大程度上仍是未知的，需要后期通过实验来确定其精确功能。本研究通过对板栗Hsp90基因家族的系统发育和在胚珠发育过程中的表达情况进行分析，为未来CmHsp90的综合功能分析奠定了坚实的基础。

图 1 枝条基径随着枝深度、胸径的分布

Figure 1. Distribution of branch base diameter with depth into crown and DBH

下载: 全尺寸图片幻灯片

图 2 基础模型（a）与混合模型包括广义正定矩阵（b）、幂函数（c）、指数函数（d）残差分布

Figure 2. Residual distribution of basic model (a) and mixed model with generalized positive definite matrix (b), mixed model with power function (c), and mixed model with exponential function

下载: 全尺寸图片幻灯片

图 3 枝条基径基础与混合模型预测值分布

1 ~ 3为幼龄，4 ~ 12为中龄，13 ~ 16为近熟，17 ~ 18为成熟。1−3 are young age, 4−12 are middle age, 13−16 are near mature, 17−18 are mature.

Figure 3. Distribution of predicted values of branch base diameter by basic and mixed models

下载: 全尺寸图片幻灯片

图 4 不同龄组枝条基径分布

Figure 4. Distribution of branch base diameter of different age groups

下载: 全尺寸图片幻灯片

表 1 长白落叶松样地、解析木及枝条因子统计

Table 1 Statistics of sample plots, analytic trees and branch attributes for Larix olgensis

因子 Factor	建模数据 Fitting data			检验数据 Validating data
因子 Factor	最大值 Max.	最小值 Min.	均值 Mean	最大值 Max.	最小值 Min.	均值 Mean
样地、样木数 Number of sample plot and sample tree	18(幼龄3、中龄9、近熟4、成熟2) 18 (young age 3, middle age 9, near mature 4, mature 2)			6(幼龄2、中龄2、近熟1、成熟1) 6 (young age 2, middle age 2, near mature 1, mature 1)
坡度 Slope/(°)	15	0	8	10	0	4
海拔 Altitude/m	376	0	304	456	266	380
立地指数 Site index	23	17	20	22	17	20
林分平均胸径 Average DBH of stand/cm	29.0	4.0	16.5	21.2	8.1	15.8
林分密度/(株·hm⁻²) Stand density/(plant·ha⁻¹)	2 800	433	858	2 617	566	1 105
枝条数 Branch number		2 089			700
胸径 DBH/cm	28.2	4.5	16.8	20.9	8.2	15.1
年龄/a Age/year	55	8	27	44	11	24
冠长 Crown length/m	13.5	4.0	8.4	10.3	5.3	6.6
着枝深度 Depth into crown/m	11.50	0.02	3.60	10.30	0.10	3.40
枝条基径 Branch base diameter/mm	52.0	1.4	14.4	45.0	2.0	12.4
枝条长度 Branch length/m	4.0	0.1	1.4	14.2	0.1	1.2

下载: 导出CSV

表 2 长白落叶松枝条基径基础及改进模型

Table 2 Basic and improved models of branch base diameter for Larix olgensis

模型名称 Model name	模型编号 Model No.	基础模型形式 Basic model form	模型编号 Model No.	改进模型形式 Improved model form
Gompertz	1	${\mathrm{BD}}=a{\rm{e}}^{(-b{\rm{e}}^{-c{\mathrm{DINC}}})}$	5	${\mathrm{BD}}=a{\rm{e}}^{(-b{\rm{e}}^{-c{\mathrm{DINC}}})}{\rm{e}}^{\left({{\mathrm{DBH}}}^{d}\right)}$
Mitscherlich	2	${\mathrm{BD}}=a(1-b{\rm{e}}^{\left(-c{\mathrm{DINC}}\right)})$	6	${\mathrm{BD}}=a(1-b{\rm{e}}^{\left(-c{\mathrm{DINC}}\right)}){\rm{e}}^{\left({{\mathrm{DBH}}}^{d}\right)}$
Logistic	3	${\mathrm{BD}}=a/(1+b{\rm{e}}^{\left(-c{\mathrm{DINC}}\right)})$	7	${\mathrm{BD}}=a{\rm{e}}^{\left({{\mathrm{DBH}}}^{d}\right)}/(1+b{\rm{e}}^{\left(-c{\mathrm{DINC}}\right)})$
单分子式 Monomolecular formula	4	${\mathrm{BD}}=a(1-{\rm{e}}^{\left(-b{\mathrm{DINC}}\right)})$	8	${\mathrm{BD}}=a(1-{\rm{e}}^{\left(-b{\mathrm{DINC}}\right)}){\rm{e}}^{\left({{\mathrm{DBH}}}^{c}\right)}$
注：BD和DINC分别是一级枝条基径和着枝深度；DBH是单木胸径；a、b、c、d是待拟合的参数。Notes: BD and DINC are base diameter and depth into crown of primary branch, respectively; DBH is individual tree DBH; a, b, c and d are parameters to be fitted.

下载: 导出CSV

表 3 基础及改进模型拟合与检验结果

Table 3 Fitting and validating results of basic and improved models

项目 Item	模型编号 Model No.	拟合优度 Goodness of fitting		检验指标 Validating index
项目 Item	模型编号 Model No.	均方根误差 RMSE	$R_{\mathrm{a}\mathrm{d}\mathrm{j} }^{2}$	平均相对误差 MAE	平均相对误差绝对值 MRAE
基础模型 Basic model	1	6.080 7	0.512 0	4.660 6	0.533 8
	2	6.095 5	0.509 7	4.675 3	0.536 1
	3	6.076 1	0.512 9	4.663 5	0.536 0
	4	6.155 4	0.500 2	4.687 3	0.521 2
改进模型 Improved model	5	5.518 8	0.597 9	3.727 4	0.402 4
	6	5.534 9	0.595 5	3.746 6	0.405 9
	7	5.520 8	0.597 6	3.732 2	0.405 4
	8	5.552 7	0.593 1	3.745 1	0.397 7

下载: 导出CSV

表 4 不同随机参数最优混合模型拟合结果比较

Table 4 Comparison in fitting results of optimal mixed models with different random parameters

随机参数个数 Number of random parameter	模型编号 Model No.	随机参数 Random parameter		统计指标 Statistical index			似然比检验 Likelihood ratio (LRT) test
随机参数个数 Number of random parameter	模型编号 Model No.	龄组水平 Age group level	单木水平 Individual tree level	AIC	BIC	Loglik	似然比 LRT	P
2	5-1	c	b	12 728.35	12 767.86	−6 357.175
3	5-2	b	c、d	12 645.05	12 695.85	−6 313.523	87.303 6	< 0.000 1
4	5-3	b	b、c、d	12 621.67	12 689.40	−6 298.833	29.380 4	< 0.000 1
5	5-4	b、d	b、c、d	12 625.67	12 704.69	−6 298.834	0.001 3	0.999 4
6	5-5	a、c、d	b、c、d	12 633.64	12 729.59	−6 299.819	1.970 9	0.578 5
7	5-6	a、b、c、d	a、b、d	12 665.63	12 784.16	−6 311.813	23.988 7	0.000 1
8	5-7	a、b、c、d	a、b、c、d	12 701.66	12 842.77	−6 325.831	212.709 5	< 0.000 1

下载: 导出CSV

表 5 不同方差协方差结构拟合结果比较

Table 5 Comparison in fitting results of different variance-covariance structures

方差−协方差结构 Variance-covariance structure	AIC	BIC	Loglik	似然比 LRT	P
广义正定矩阵 Generalized positive definite matrix	12 621.67	12 689.4	−6 298.83
对角矩阵 Diagonal matrix	12 625.01	12 687.1	−6 301.50	5.341 0	0.020 8

下载: 导出CSV

表 6 不同异方差结构混合模型拟合结果比较

Table 6 Comparison in fitting results of mixed model with different heteroscedasticity structures

异方差结构 Heteroscedasticity structure	AIC	BIC	Loglik	似然比 LRT	P
无 None	12 621.67	12 689.40	−6 298.830
幂函数 Power function	12 151.53	12 230.55	−6 061.764	474.14	< 0.000 1
指数函数 Exponential function	12 220.72	12 294.10	−6 097.359	71.19	< 0.000 1

下载: 导出CSV

表 7 基础与混合模型拟合结果及检验

Table 7 Fitting and validating results of basic and mixed models

模型形式 Model form	参数 Parameter (标准差 SD)				拟合优度 Goodness of fitting		评价指标 Evaluating index
模型形式 Model form	a	b	c	d	RMSE	$R_{\mathrm{a}\mathrm{d}\mathrm{j} }^{2}$	MAE	MRAE
基础模型(5) Basic model (5)	3.172 8	2.017 4	0.384 9	0.259 3	5.518 8	0.597 9	3.727 4	0.402 4
基础模型(5) Basic model (5)	(0.190 4)	(0.069 4)	(0.007 6)	(0.023 4)
混合模型(5-3) Mixed model (5-3)	2.088 1	1.882 3	0.379 6	0.328 7	4.768 4	0.699 8	3.705 8	0.391 6
	(0.194 6)	(0.164 5)	(0.040 4)	(0.014 3)
异方差(幂函数) Heteroscedasticity (power function)	$\alpha$ = 0.63
模型方差 Model variance	${\sigma }^{2}$ = 6.597 8
方差协方差结构 Variance-covariance structure	${{D} }_1=\left\|3.82 \times 10^{-34}\right\|$				${{D}}_2=\left\|\begin{array}{ccc}\;\;\;0.450 \; 9& \;\;\;0.257 \; 0& -0.143 \; 0\\ \;\;\;0.257 \; 0& \;\;\;0.021 \; 4& -0.752 \; 0\\ -0.143 \; 0& -0.752 \; 0& \;\;\;0.000 \; 4\end{array}\right\|$
注：D₁、D₂分别是龄组、单木水平的方差协方差结构。Notes: D₁ and D₂ are variance-covariance structures of age group and individual tree level, respectively.

下载: 导出CSV

表 8 固定效应与随机效应检验结果的比较

Table 8 Comparison of validating results of fixed effect and random effect

单木编号 Individual tree No.	固定效应 Fixed effect		随机效应 Random effect
单木编号 Individual tree No.	平均绝对误差 MAE	平均相对误差绝对值 MRAE	平均绝对误差 MAE	平均相对误差绝对值 MRAE
1	2.691 1	0.457 0	2.309 9	0.364 1
2	2.772 3	0.296 4	2.477 1	0.229 6
3	5.490 9	0.264 6	4.368 7	0.227 2
4	3.579 9	0.274 1	3.420 8	0.267 7
5	3.913 0	0.469 6	3.753 1	0.340 8
6	4.746 1	0.687 5	2.902 9	0.359 0

下载: 导出CSV

参考文献(25)

[1]	Brown P L, Doley D, Keenan R J. Stem and crown dimensions as predictors of thinning responses in a crowded tropical rainforest plantation of Flindersia brayleyana F. Muell[J]. Forest Ecology and Management, 2004, 196(2): 379−392.
[2]	Maguire D A, Kershaw J A, Hann D W. Predicting the effects of silvicultural regime on branch size and crown wood core in Douglas-fir[J]. Forest Science, 1991, 37(5): 1409−1428.
[3]	王小青, 刘杏娥, 任海青. 树冠特征对小黑杨木材性质和生长量的影响研究[J]. 林业科学研究, 2007, 20(6):801−806. doi: 10.3321/j.issn:1001-1498.2007.06.011. Wang X Q, Liu X E, Ren H Q. Effects of crown attributes on wood characteristics and increments of Populus × xiaohei[J]. Forest Research, 2007, 20(6): 801−806. doi: 10.3321/j.issn:1001-1498.2007.06.011.
[4]	Groot A, Schneider R. Predicting maximum branch diameter from crown dimensions, stand characteristics and tree species[J]. Forestry Chronicle, 2011, 87(4): 542−551.
[5]	孙晓, 李春友, 贺红月, 等. ‘107杨’一级枝条基径和长度的动态模拟研究[J]. 林业与生态科学, 2018, 33(4):364−372. Sun X, Li C Y, He H Y, et al. Dynamic simulation of length and diameter of first branches of ‘107 poplar’[J]. Forestry and Ecological Sciences, 2018, 33(4): 364−372.
[6]	李春明. 基于两层次线性混合效应模型的杉木林单木胸径生长量模型[J]. 林业科学, 2012, 48(3):66−73. doi: 10.11707/j.1001-7488.20120311. Li C M. Individual tree diameter increment model for Chinese fir plantation based on two-level linear mixed effects models[J]. Scientia Silvae Sinicae, 2012, 48(3): 66−73. doi: 10.11707/j.1001-7488.20120311.
[7]	Yang Y, Huang S. Allometric modelling of crown width for white spruce by fixed- and mixed-effects models[J]. The Forestry Chronicle, 2017, 93(2): 138−147.
[8]	朱万才, 贾炜玮. 基于随机效应的红松人工林一级枝条动态生长模型[J]. 森林工程, 2015, 31(4):26−32. doi: 10.3969/j.issn.1001-005X.2015.04.007. Zhu W C, Jia W W. Dynamic growth model for First-hierarchy branch of Korean pine plantation based on mixed effect model[J]. Forest Engineering, 2015, 31(4): 26−32. doi: 10.3969/j.issn.1001-005X.2015.04.007.
[9]	姜立春, 李凤日, 张锐. 基于线性混合模型的落叶松枝条基径模型[J]. 林业科学研究, 2012, 25(4):464−469. doi: 10.3969/j.issn.1001-1498.2012.04.009. Jiang L C, Li F R, Zhang R. Modeling branch diameter with linear mixed effects for Dahurian larch[J]. Forest Research, 2012, 25(4): 464−469. doi: 10.3969/j.issn.1001-1498.2012.04.009.
[10]	Chun-Sheng W, Cheng T, Sebastian H, et al. Branch development of five-year-old Betula alnoides plantations in response to planting density[J/OL]. Forests, 2018, 9(1): 42 [2019−11−12]. https://doi.org/10.3390/f9010042.
[11]	Weiskittel A R, Maguire D A, Monserud R A. Response of branch growth and mortality to silvicultural treatments in coastal Douglas-fir plantations: implications for predicting tree growth[J]. Forest Ecology and Management, 2007, 251(3): 182−194.
[12]	姜立春, 潘莹, 李耀翔. 兴安落叶松枝条特征联立方程组模型及树冠形状模拟[J]. 北京林业大学学报, 2016, 38(6):1−7. Jiang L C, Pan Y, Li Y X. Model systems of branch characteristics and crown profile simulation for Larix gmelinii[J]. Journal of Beijing Forestry University, 2016, 38(6): 1−7.
[13]	陈东升, 孙晓梅, 李凤日. 落叶松人工林枝条直径和长度的非线性混合模型[J]. 南京林业大学学报(自然科学版), 2015, 39(6):74−80. Chen D S, Sun X M, Li F R. Nonlinear mixed models of branch diameter and length in larch plantation[J]. Journal of Nanjing Forestry University (Natural Sciences Edition), 2015, 39(6): 74−80.
[14]	Lemay A, Pamerleau-Couture É, Krause C. Maximum branch diameter in black spruce following partial cutting and clearcutting[J/OL]. Forests 2019, 10(10): 913 [2020−01−03]. https://www.mdpi.com/1999-4907/10/10/913.
[15]	Jia W, Chen D. Nonlinear mixed-effects height to crown base and crown length dynamic models using the branch mortality technique for a Korean larch (Larix olgensis) plantations in northeast China[J]. Journal of Forestry Research, 2019, 30(6): 2095−2109.
[16]	贾炜玮, 孙守强, 李凤日, 等. 基于混合模型的红松人工林枝条动态研究[J]. 植物研究, 2015, 35(3):425−430. doi: 10.7525/j.issn.1673-5102.2015.03.016. Jia W W, Sun S Q, Li F R, et al. Branch dynamics for the Korean pine plantation based on linear mixed model[J]. Bulletin of Botanical Research, 2015, 35(3): 425−430. doi: 10.7525/j.issn.1673-5102.2015.03.016.
[17]	王春红, 李凤日, 贾炜玮, 等. 基于非线性混合模型的红松人工林枝条生长[J]. 应用生态学报, 2013, 24(7):1945−1952. Wang C H, Li F R, Jia W W, et al. Branch growth of Korean pine plantation based on nonlinear mixed model[J]. Chinese Journal of Applied Ecology, 2013, 24(7): 1945−1952.
[18]	Sharma R P, Vacek Z, Vacek S. Individual tree crown width models for Norway spruce and European beech in Czech Republic[J]. Forest Ecology and Management, 2016, 366: 208−220.
[19]	高慧淋, 董利虎, 李凤日. 基于混合效应的人工落叶松树冠轮廓模型[J]. 林业科学, 2017, 53(3):84−93. doi: 10.11707/j.1001-7488.20170310. Gao H L, Dong L H, Li F R. Crown shape model for Larix olgensis plantation based on mixed effect[J]. Forest Research, 2017, 53(3): 84−93. doi: 10.11707/j.1001-7488.20170310.
[20]	Fu L, Sun H, Sharma R P, et al. Nonlinear mixed-effects crown width models for individual trees of Chinese fir (Cunninghamia lanceolata) in south-central China[J]. Forest Ecology and Management, 2013, 302: 210−220.
[21]	罗恒春, 张超, 魏安超, 等. 云南松林分平均高生长模型及模型参数环境解释[J]. 北京林业大学学报, 2018, 40(4):67−75. Luo H C, Zhang C, Wei A C, et al. Stand average height growth model and environmental interpretation in model parameter of Pinus yunnanensis[J]. Journal of Beijing Forestry University, 2018, 40(4): 67−75.
[22]	洪奕丰, 陈东升, 申佳朋, 等. 长白落叶松人工林单木和林分水平的相容性生物量模型研究[J]. 林业科学研究, 2019, 32(4):33−40. Hong Y F, Chen D S, Shen J P, et al. Compatible biomass models forLarix olgensis plantation based on tree-level and stand-level[J]. Forest Research, 2019, 32(4): 33−40.
[23]	罗恒春, 张超, 魏安超, 等. 云南松林分平均胸径生长模型及模型参数环境解释[J]. 浙江农林大学学报, 2018, 35(6):1079−1087. doi: 10.11833/j.issn.2095-0756.2018.06.011. Luo H C, Zhang C, Wei A C, et al. Average DBH growth model of a stand with environmental parameters for Pinus yunnanensis in central Yunnan, China[J]. Journal of Zhejiang A&F University, 2018, 35(6): 1079−1087. doi: 10.11833/j.issn.2095-0756.2018.06.011.
[24]	Huff S, Poudel K P, Ritchie M, et al. Quantifying aboveground biomass for common shrubs in northeastern California using nonlinear mixed effect models[J]. Forest Ecology and Management, 2018, 424: 154−163.
[25]	姜立春, 张锐, 李凤日. 基于线性混合模型的落叶松枝条长度和角度模型[J]. 林业科学, 2012, 48(5):53−60. doi: 10.11707/j.1001-7488.20120508. Jiang L C, Zhang R, Li F R. Modeling branch length and branch angle with linear mixed effects for Dahurian larch[J]. Scientia Silvae Sinicae, 2012, 48(5): 53−60. doi: 10.11707/j.1001-7488.20120508.

施引文献(16)

期刊类型引用(7)

1.	周浪，樊坤，瞿华，张丁然. 基于ECA注意力机制改进的EfficientNet-E模型的森林火灾识别. 华南理工大学学报(自然科学版). 2024(02): 42-49 . 百度学术
2.	王宇虹，陈仲榆，杨晓丹，赵鲁强，袁晓玉，梁莉. 重庆两场森林火灾蔓延特征的数值模拟. 气象科技. 2024(02): 205-217 . 百度学术
3.	何乃磊，张金生，林文树. 基于深度学习多目标检测技术的林火图像识别研究. 南京林业大学学报(自然科学版). 2024(03): 207-218 . 百度学术
4.	李宝民，王小鹏，孙茜容，张军平. 基于概率两阶段CenterNet2的林火图像预警检测方法. 计算机工程与科学. 2023(10): 1884-1890 . 百度学术
5.	刘九庆，项前，王宇航. 基于SIFT算法和改进的RANSAC算法对森林火灾的图像识别与试验研究. 森林工程. 2022(06): 96-103 . 百度学术
6.	李梓雯. 森林防火现状问题与防火体系建设对策研究——以河南省新乡市为例. 森林防火. 2022(01): 6-9+14 . 百度学术
7.	骆晨，潘卫军，朱新平，王玄. 通用航空森林火灾救灾决策模型研究. 消防科学与技术. 2021(12): 1784-1787 . 百度学术

其他类型引用(9)

资源附件(0)

图(4) / 表(8)

计量

文章访问数: 1728
HTML全文浏览量: 512
PDF下载量: 115
被引次数: 16

1. 材料与方法
1.1 试验材料
1.2 研究方法
1.2.1 Hsp90基因家族成员的鉴定
1.2.2 Hsp90基因家族蛋白序列及结构分析
1.2.3 Hsp90基因家族启动子的顺式作用元件分析
1.2.4 Hsp90基因家族多序列比对与系统发育进化树构建
1.2.5 Hsp90基因在胚珠不同发育时期的表达分析
2. 结果与分析
2.1 CmHsp90家族基因的鉴定
2.2 CmHsp90基因家族蛋白的结构分析
2.3 CmHSP90基因家族的顺式作用元件预测
2.4 CmHsp90基因家族系统进化分析
2.5 CmHsp90基因家族成员在胚发育过程中的表达分析
3. 讨　　论

1. 材料与方法
1.1 试验材料
1.2 研究方法
1.2.1 Hsp90基因家族成员的鉴定
1.2.2 Hsp90基因家族蛋白序列及结构分析
1.2.3 Hsp90基因家族启动子的顺式作用元件分析
1.2.4 Hsp90基因家族多序列比对与系统发育进化树构建
1.2.5 Hsp90基因在胚珠不同发育时期的表达分析
2. 结果与分析
2.1 CmHsp90家族基因的鉴定
2.2 CmHsp90基因家族蛋白的结构分析
2.3 CmHSP90基因家族的顺式作用元件预测
2.4 CmHsp90基因家族系统进化分析
2.5 CmHsp90基因家族成员在胚发育过程中的表达分析
3. 讨　　论

参考文献(25)

施引文献(16)

资源附件(0)

基于混合效应的长白落叶松一级枝条基径预估模型

作者简介: 靳晓娟。主要研究方向：森林资源监测与模型模拟。Email：1072733074@qq.com 地址：100083 北京市海淀区清华东路 35 号北京林业大学林学院

责任作者: 孙玉军，教授，博士生导师。主要研究方向：森林资源监测与模型。Email：sunyj@bjfu.edu.cn 地址：同上

计量

出版历程