Advances in genomic selection and its development trend in forest
-
摘要: 随着新一代基因组测序技术的快速发展,基因组选择技术在促进优良基因型精准高效选育方面展现了前所未有的应用前景。近年来,基因组选择在动植物数量性状遗传育种领域的研究进展引起了广泛关注,关于其在林木改良驯化中的应用 也逐渐被报道。本文通过综述基因组选择的基本概况、主要模型方法及其在动植物中的研究进展,进一步探讨了基因组选择在林木育种研究中的现状和发展趋势,强调了对预测模型优化与机器学习等新兴技术的引入与方法创新,提出了联合利用全基因组关联分析与基因组编辑技术的优化育种方案,为加快林木优良品种的精准选育提供了新思路。Abstract: With the rapid development of the next-generation of genome sequencing technologies, genomic selection has shown an unprecedented potential in promoting the accurate and efficient selection breeding of elite genotypes. The investigation on genomic selection in the field of genetic breeding for quantitative traits in plants and animals had been attracted more attention, and particularly the recent applications on the improvement and breeding in forest were increasingly reported. Here we summarized the basic theories and main model approaches of genomic selection, and reviewed the advances of genomic selection in animal and plant breeding. We further discussed the research status and prospects of genomic selection in woody plants, emphasized the optimization of prediction models and innovation of machine learning-based methods, and provided the integrated breeding strategies combining with genome wide association studies and genome-editing technologies. These comprehensive breeding systems provide insights into the accurate selection and breeding for excellent varieties in forest trees.
-
Keywords:
- forest /
- genomic selection /
- model optimization /
- molecular breeding /
- breeding value
-
20世纪80年代,随着分子生物学技术的飞速发展,以分子标记辅助选择(molecular marker-assisted selection,MAS)策略为导向的现代育种技术体系,被认为是加速多年生木本植物驯化与遗传改良的重要途径。该策略提出的遗传学理论基础是利用家系分离群体构建遗传连锁图谱,并进行标记与性状间的遗传连锁分析,以此实现数量性状位点(quantitative trait loci,QTL)的定位[1];在木本植物复杂性状遗传基础研究方面取得了显著进展[2-6]。但由于林木遗传作图大多基于F1、F2或BC1等低世代家系群体,遗传变异丰富度较低和染色体重组事件有限,导致QTL作图分辨率低且其遗传效应往往被高估,造成数量性状的遗传定位不准确,难以挖掘有效的功能育种标记。近几年,随着基于自然群体或种质资源群体连锁不平衡(linkage disequilibrium,LD)理论的关联遗传学策略的提出,为解析数量性状的遗传基础提供了新的途径。然而,多年生林木育种群体LD衰退较快,基因组存在大量被忽略的稀有等位变异,导致在遗传作图中仅检测主效QTL,而忽略了其他微效基因的遗传贡献,导致“遗传力丢失”现象。因此,当前MAS技术在林木微效基因控制的目标性状遗传改良中解析精度较低,难以规模化应用[7]。
鉴于MAS策略存在的不足,Meuwissen等[2]提出了基因组选择(genomic selection,GS)育种策略。它与MAS的根本区别是,GS是一种全基因组范围的标记辅助选择方法,主要通过全基因组大量的遗传标记信息计算出不同染色体片段的育种值,然后估算出个体基因组范围的总育种值并进行未知群体的选择。GS育种的理论基础是假设标记与相邻QTL处于LD状态,从而保证相同标记估计的不同群体染色体片段效应也相同。因此,GS避免了由于小效应标记偏差导致的预测准确性差异,大大提高了育种值估计的精确性。特别适合于育种周期较长、目标性状遗传复杂、表型测量难度大或成本高的林木树种,可显著提升目标性状的遗传改良精度,并显著降低操作成本,发展与应用前景广阔。
本文结合笔者团队在林木分子育种领域的研究进展,通过综述GS的基本原理、统计学模型以及在动植物领域的应用及最新研究成果,提出了林木GS育种未来发展策略,以期为林木复杂性状遗传改良提供理论参考与技术支持。
1. 基因组选择概述
基因组选择的实施主要包括两个步骤:一是在训练群体(training population,TP)中根据已知的个体基因型数据与表型变异数据,估计出不同染色体片段的效应,以此构建个体全基因组估计育种值(genomic estimated breeding value,GEBV)预测模型;二是在育种群体(breeding population,BP)中利用该模型对基因型可知、但表型未知的个体进行早期表型预测。因此,利用GS不仅可减少数量性状“遗传力丢失”,提高选育精度,而且可明显缩短育种周期,真正实现苗期精准选育。
已有GS研究表明,不同类型的预测模型因其在处理复杂性状变异时的假设不同而得到不同的准确度与效率。GS的典型混合模型为:
y=Xβ+Zα+ε[3] 式中:y是n × 1的表型向量;β是非遗传效应的载体,即固定效应;X是与β对应的关联矩阵;Z是n × k的基因型矩阵;α是具有设计矩阵Z的遗传效应的k × 1的向量,ε是残差的向量。即利用X和Z矩阵预测表型y,打破了利用个体间的亲缘系数预测育种值的传统方法。
全基因组估计育种值的精准度决定了林木基因组选择育种的效率与精度,是GS技术相比于其他分子标记辅助技术的优势之处。使用GS预测估算林木育种值时,必须考虑到影响基因组选择模型精度的各种因素,同时考虑到木本植物区别于动物与作物基因组的复杂特征。因此,有效训练群体大小及结构、标记密度、估算模型种类等因素都会影响GS模型育种值的估算。
在GS的应用中,育种值的准确度会受到训练群体大小与结构的影响,一般而言,GS预测准确性会随着训练群体的增大而得到提高;在训练群体较大的林木群体中,GS比表型选择和传统MAS产生更大的单位时间和单位成本的遗传增益。例如,Grattapaglia[8]利用多个林木树种开展GS理论研究,通过曲线对训练个体集N = 200、500、1 000、2 000、4 000和8 000发现,当N = 2 000之前,GS的准确性随训练群体数目的增加而不断提高,表明训练群体的扩大可以显著提高GS准确性;当训练群体个体数增加到2 000以上时,GS的精度变化趋于平稳。另外,当群体个体数目为1 000时,在高标记密度情况下,无论有效种群大小,准确率都高于0.8,该结果可较好地反映出实验精度与训练群体大小的成本支出的平衡关系。
在分子标记类型中,单核苷酸多态性位点(single nucleotide polymorphisms,SNP)因其全基因组分布广泛、遗传稳定性高和基因分型比较规律等优点,是用于GS研究最理想的标记类型。全基因组SNP标记密度决定了目标性状GS预测方法的准确性,且发现GS准确性一般随标记密度的增加而增加。另外,标记密度会受到训练群体LD水平影响,即较高的LD提高了标记与数量性状位点之间连锁的可能性,可以提高基因组选择的准确性[9-10];尤其是标记数量越多,越容易检测到与QTL具有显著LD水平的候选位点。然而,随着育种世代的增加,标记位点与QTL间LD程度会逐渐降低,进而导致GS准确性降低,因此在GS研究中单标记或单倍型效应经过若干世代就需要重新估计。
由于不同GS模型具有不同的标记效应与方差假设,使得在选取不同GS模型时预测目标群体的准确度不同。一般而言,最佳线性无偏预测(best linear unbiased prediction,BLUP)及贝叶斯分类算法(Bayes)具有较高的育种值估测精度,而最小二乘法(least square,LS)相对较差,且多利用固定的标记效应进行预测。在林木数量性状GS研究时,应充分根据研究树种生物学特征和已有研究基础进行估算模型的选择和利用。
2. 基因组选择研究进展
目前,基因组选择理论与技术在重要家畜与作物GS模型开发、实验算法与变量优化计算、以及联合交叉运用等方面创造了一系列成熟的育种值估算方法与GS策略,在动物和作物数量性状遗传改良研究中发展较为成熟,为多年生木本植物GS育种研究提供了理论支持与技术参考,对于新兴分子设计育种技术具有借鉴意义。
2.1 基因组选择统计方法
选择恰当的统计学模型提高基因组育种值估测精度,是目标性状GS育种中的关键环节。目前,常用基因组育种模型(表1),例如LS、BLUP以及Bayes算法,一般需要根据物种目标性状QTL数目、遗传率大小和群体遗传背景等因素来进行选择应用。
表 1 常用的基因组选择模型Table 1. Common models for genomic selection模型
Model基本原理
Basic principle标记效应
Marker effect方差假设
Variance assumptionQTL效应
Effect of
QTLs估计准确度
Estimation accuracy参考文献
Reference最小二乘法
Least square method多元线性回归方程
Multiple linear regression equation固定
Fixed— 高估
Overvalued最低
Minimum[25-26] 最佳线性无偏预测法
Best linear unbiased prediction (RR-BLUP)预测变量的均匀收缩为零允许标记有不均匀效果
Uniform shrinkage of the predictive variable is zero, allowing the marker to have an uneven effect随机
Random相等
Equal低估
Underestimated较高
Higher[3, 25, 27-28] 基因组最佳线性无偏估计
Genomic best linear unbiased prediction (GBLUP)矩阵G代替传统亲缘关系矩阵A
Matrix G replaces the traditional relationship matrix A随机
Random相等
Equal偏高估
Partial overvalued较高
Higher[25-27, 29] 贝叶斯A
Bayes A效应方差的先验和后验均为逆卡方分布,小标记收缩效果为零
Prior and posterior effects of variance are inverse chi-square distribution, and the shrinkage effect of small markers is zero随机
Random所有SNP均有效应
All SNPs have an effect更准确估计
More accurate estimation最高,但低于贝叶斯
Max., but lower than Bayes B[3, 22, 28,30] 贝叶斯B
Bayes B效应方差的先验和后验均为逆卡方分布,收缩和变量选择方法
Prior and posterior effects of variance are inverse chi-square distribution, contraction and variable selection methods随机
Random大多数SNP无效应
Most SNPs have no effect更准确估计
More accurate estimation最高,高于贝叶斯
Max., higher than Bayes B[3, 22, 26, 30] 其中,LS方法基于简单的多元线性回归方程原理,操作系统较为简单,无需估计所有标记效应,主要应用于早期的GS育种研究。但是先前研究表明,该方法筛选出来的标记效应被过高估计,导致预测准确度下降[11-13]。例如,Lund等[14]利用LS等多种固定效应模型来预测模拟数据的GEBV,发现模型预测能力随着SNP标记数目增多而降低,且所有固定效应模型都严重高估了育种值。BLUP方法主要基于岭回归(RR)同等混合模型原理被提出[15],与普通回归模型相比,该方法在标记高度相关时具有较高的稳定性,在基因组选择技术中被广泛应用。在BLUP方法基础上,优化开发出两种更为精确的GS方法:一种是GBLUP法,其原理是利用全基因组关系矩阵G替换传统方法中的个体亲缘相关矩阵A,进而估算个体的估计育种值[16];其中育种值由亨德森混合模型方程计算得出[17]。Gao等[18]在北欧荷斯坦公牛(Nordic holstein)群体开展GBLUP预测表明,具有多基因效应的预测方法可靠性比简单GBLUP高0.3%,且基因组预测偏差较小。另一种是随机回归最佳线性无偏预测法(random regression-best linear unbiased prediction,RR-BLUP),也称岭回归。该方法假定基因组中所有片段位点的效应具有共同的方差,并且可以同时估计所有的标记效应,以此避免了LS产生的标记效应过高的问题,显著提高了预测准确度[19]。研究人员利用42个二系春大麦(Hordeum vulgare)自交系的标记数据,模拟了不同自交系杂交组合的高、低LD群体,结果表明当QTL数目增加或性状具有较高的遗传力时,RR-BLUP法的准确性变得更高[20];Endelman等[21]利用RR-BLUP的R软件包,基于对优良子代值鉴定的交叉验证测试,实现了RR-BLUP法在小麦(Triticum aestivum)和玉米(Zea mays)产量性状上的高准确度预测。
近年来基因组选择技术的不断发展,使得Bayes算法成为基因组选择中最常应用的统计方法。该方法针对SNP标记效应及其方差假定先验分布的不同,在给定训练数据时预测标记效应的后验分布,从而开发出精确度更高的GEBV预测方法[22]。Bayes算法依据不同标记效应有不同的假设,主要分为Bayes A、Bayes B、Bayes Cπ、Bayesian LASSO等,其对QTL的标记数量敏感,并随着QTL数量的增加预测精度下降。Hayes等[23]使用Bayes方法对多品种奶牛训练群体研究时发现,其GEBV的预测准确度比使用纯品种训练群体高出13%,因此,在精细定位QTL的多品种群体中,Bayes方法为目标性状育种值估测提供了更高的准确度。同样,Shikha等[24]在对玉米基因组抗旱性状选择研究中比较了7种GS模型的预测精度,结果发现Bayes B模型具有最大准确度。针对Bayes A和Bayes B中SNP效应方差的先验分布为逆卡方分布、自由度小等缺陷[22],使得优化后的Bayes Cπ和Bayes Dπ在GS育种值估计方法中被更多的选择利用。上述研究表明Bayes法在多性状群体的预测中有重要的应用意义。随着生物学、农林科学与统计学的发展与交叉融合,针对不同物种群体、育种目标等需求,利用R语言等工具优化或开发更加友好高效、个性化的GS估测模型,可显著提高选择育种研究进展。
2.2 动植物GS研究进展
近年来,随着基因组选择技术的飞速发展,越来越多的模型方法被用于动植物的遗传改良研究中,为动植物新品种的选育提供了重要的理论依据。下面将主要介绍GS育种技术在动物及作物植物中的主要研究进展,以期为多年生木本植物复杂性状的遗传改良提供理论与方法借鉴。
基因组选择作为一种依赖于高通量测序而不需要对功能基因进行定位的预测方法[31],在动物育种中首先开展并具有里程碑式的意义。研究人员对加拿大奶牛利用GS的优势策略与传统测试策略进行比较,结果表明利用GS技术使得后代公牛生产成本降低了92%,基因预测精度增加了2倍[32]。同时,与传统育种方法比较,基因组选择技术可以降低近亲繁殖率且增加遗传增益。Lillehammer等[33]通过GS技术对近亲繁殖率相同的公牛亲本进行子代精选,发现其遗传增益相比传统方法增加了13%,表明GS在降低近交率的同时仍能增加遗传精度,对于降低畜牧养殖成本具有显著应用价值;但由于动物家系群体大多亲缘关系较近,即使采用GS技术也难以获得预期的遗传增益值。然而林木物种具有基因组杂合度高、驯化改良周期短,易开展远缘杂交等特点,利用GS策略开展目标性状的选育与亲本效应估算,可打破传统育种预测的遗传增益值局限,提高选育精度和效率。
通常农作物的繁殖周期相对较短。例如在玉米育种研究中,完成一个田间育种的试验周期大约是两年时间[34]。作物GS策略对比表型选择的优势主要体现在GS可用于苗期的分子选择,而不需要测定个体表型[35],以此降低了复杂性状的育种时间成本。因此若将GS应用于多年生林木研究中,必将显著缩短林木遗传改良期。Beyene等[36]对干旱胁迫环境下的8个双亲玉米种群利用基因组选择估计粮食产量的遗传增益,利用干旱胁迫和充足水分两种处理对群体杂交测试结果进行评估,发现利用GS的C3杂交种比传统谱系育种的C2杂交种产量高7.3%,表明在干旱胁迫下,基因组选择比基于谱系的常规表型选择更能提高热带玉米籽粒产量的遗传增益,为开展不同逆境条件下造林树种的遗传改良提供了借鉴。基因组选择作为一种旨在提高育种效率和精度的新兴创新技术,已经被广泛应用于小麦和水稻等作物中。例如,Spindel等[37]首次对363个水稻优良品系进行了全基因组关联分析(genome wide association study,GWAS)和五倍GS交叉验证,利用GS发现所有种系的籽粒产量、株高和开花时间预测结果均优于仅基于系谱的传统预测,揭示了以GWAS解释遗传基础和以GS预测优异种质育种潜力的联合方法已成为作物育种的有效工具。因此,在遗传基础薄弱、育种周期较长的木本物种中,联合利用GWAS技术与GS工具,可显著推动木本植物复杂性状关键育种基因的挖掘;同时在林木核心种质资源的辅助筛选、目标性状的后向选择及其遗传增益的提升方面将具有重要应用前景。
2.3 木本植物基因组选择研究进展
林木树种具有育种周期长,目标性状遗传构成复杂、研究基础薄弱等特点,与农作物和动物育种相比,林木遗传育种尚处于起步阶段。通常,如何提高选育精度并显著缩短育种周期,一直是多年生木本植物遗传改良的研究难点;其次,木本植物野生资源与家系育种资源遗传变异丰富,如何充分利用杂种优势实现目标性状遗传增益的大幅度提高,是林木遗传育种研究的前沿热点[38]。鉴于上述研究,如果在木本植物中成功运用GS育种策略,其影响力将远大于其他作物或动物育种[34]。
近年来,随着高通量测序技术的飞速发展及其基因分型成本的下降,基于精准基因组信息的辅助育种研究为林木优异基因资源的发掘与利用带来了新的机遇。目前,桉树(Eucalyptus robusta)、杨树(Populus spp.)、火炬松(Pinus taeda)、挪威云杉(Picea abies)等主要森林用材树种,以及枣(Ziziphus jujuba)、核桃(Juglans regia)、板栗(Castanea mollissima)等多个经济林树种的全基因组测序研究,业已完成或正在完善升级之中[34],这些丰富的基因组测序信息数据库,为林木GS育种研究提供了关键的遗传参考信息,为构建精准估测模型提供了重要的理论基础。林木选育周期较长、数量性状遗传变异丰富、部分性状遗传力较低、且全基因组等位变异标记分布广泛且均匀,使得GS策略在多年生木本植物中具有特别的吸引力;尤其是林木具有分布广泛、多年生的大规模野生或半驯化状态的训练群体,以及较低的连锁不平衡程度更展现了GS应用于林木育种程序的优势。随着2011年巨桉(Eucalyptus grandis)基因组序列的公布,Resende等[39]在桉树中实现了GS技术首次在林木树种中的应用。该研究通过对桉树生长和木材品质性状的GS准确度预测,发现GS精度取决于性状和有效群体大小,证实了早期模拟的实验结果,开启了木本植物GS育种的新篇章。
研究人员通过模拟日本柳杉(Cryptomeria japonica)60年育种计划[40],发现在没有模型更新下,前30年内GS育种方法要优于表型选择育种方法;在模型更新后GS育种实现的遗传增益几乎是表型选择育种的两倍,使得GS手段已成为缩短针叶树种较长育种周期和降低繁殖成本的重要技术。GS改良模型消除了传统表型选择的粗放性和不稳定性,显著提高了遗传增益。Resende等[9]对针叶树火炬松(Pinus taeda)包括926个无性系的育种群体进行GS模型预测,发现与传统的BLUP表型选择相比,假设在育种周期长度减少一半的情况下,GS技术预测火炬松的胸径的效率将提高53% ~ 92%,树高的效率将提高58% ~ 112%,该方法的运用将改变林木部分复杂性状表达晚的不利特点,缩短良种选育成本与周期,从而极大的推进了木本植物的遗传改良进程。此外,Isik等[41]利用SNP标记对两代海岸松(Pinus pinaster)包含661个无性系的繁殖群体进行基因分型与GS研究,发现使用BLUP、贝叶斯岭回归和贝叶斯LASSO回归模型预测,提高了遗传标记对主干胸径和地径指标的预测能力。大量研究表明,开展木本植物GS育种存在很大的潜力和优势,但由于木本植物的有效群体数量较大,且繁殖周期长、田间试验成本高,当前林木领域的GS实践研究开展相对较少。相信随着新技术的不断优化与发展,利用GS开展林木复杂性状改良的预测研究将成为林木育种领域的前沿热点。
3. 基因组选择技术的优化与发展
鉴于目前林木GS技术的运用范围较窄、研究技术不完善和研究机制分析不透彻等现状,笔者基于研究团队在林木分子育种领域的研究进展,结合当前农林领域新技术发展与革新的实践基础,拟提出以下几个深化木本植物GS育种的研究策略。
3.1 GS模型的优化及其与MAS育种方法的联合应用
近年来,随着GS模型在动植物中的应用与发展,预测准确度已成为衡量GS方法的重要指标,全基因组育种值的估计精确度决定了该技术在林木树种遗传改良方向的应用潜力。鉴于木本植物生长繁殖周期长、多基因控制性状等特点,加上GS模型的预测精度会随着研究模型对标记效应和处理假设不同而不同,因此,根据不同木本植物群体大小与结构、标记密度、以及标记QTL之间LD程度和分布等因素,选择或开发合适的研究模型尤为重要[42]。一般而言,木本植物中预测变量(p)的数量通常远远大于个体数量(n),此时,由于最小二乘法将遗传的标记效应假定为固定效应,导致预测变量间造成多重性和过度拟合的问题,使得该模型的预测能力大大降低[42-43];相比而言,贝叶斯模型是当前木本植物GS研究使用最广泛且预测度较高的模型,且该模型一直被完善和升级。例如,Meuwissen等[2]通过模拟数据的研究表明,Bayes A和Bayes B的估计准确性比RR-BLUP方法分别提高约9%和16%;但由于其存在SNP效应方差的先验分布为逆卡方分布,以及把某个SNP效应为零的概率值π作为已知参数的缺陷[28],研究人员进一步提出了更为完善的Bayes Cπ和Bayes Dπ[44]方法,有效地提高了传统方法的效率。随着关联遗传学及其MAS策略的发展,研究人员在树木遗传改良研究中,通过联合应用基因组选择和关联遗传学方法,弥补了家系群体低LD水平和等位基因有限的局限[45],加速了对优良树种的选择与驯化。因此,如果可以实现对GS的参数和非参数模型的优化和完善,并充分发挥MAS和GS选育方法的各自优势,将为木本植物选育提供关键的技术支撑和高效率的预测精度。另外,加强对育种周期中发育早期性状(例如,生长速率、根冠比)与晚期性状(结实率、花粉活力)遗传相关性的认识,开发出可间接利用早期性状指标进行晚期目标性状的GS选育策略。
3.2 加强GS与新兴技术的交叉与应用
随着高通量测序技术的飞速发展与规模化应用,生物学领域的研究进入了“大数据”时代,GS的数据量和复杂性也随之上升,导致了以整合计算机科学、人工智能、数学、物理、统计学、和遗传学以及生物信息学等新的跨学科研究领域的诞生,以期联合数据分析、统计模型和机器学习等方法获得更准确的预测值。目前,基于神经网络方法的机器学习(machine learning)等新技术在基因组选择中得以广泛应用,对于提升基因组育种值的预测性能,促进木本植物良种选育具有重要意义。其中,神经网络方法作为机器学习中常用的预测工具,主要由相互联系的神经元层(输入层和输出层)组成,利用遗传标记构建神经元连接,形成交互网络作为机器学习统计模型,从而得以使用GS精准预测每一个表型[46],实现了计算机科学、人工智能以及生物信息的交叉运用。
此外,随机森林(random forest,RF)[25, 47-48]、随机梯度增强(stochastic gradient boosting,SGB)[40-50]和支持向量机(support vector machines,SVM)[51-54]等方法也成为了机器选择中应用较广、预测准确度较高的新方法。研究人员利用模拟群体五倍交叉验证对3种方法的预测性能进行评估比较,结果表明模拟值和预测值之间的相关性SGB和SVM的性能优于RF [55]。同时研究人员通过模拟数据发现,SGB和RF法均可应用于木本植物复杂遗传网络和上位性的交互作用研究[56],对于遗传基础复杂的数量性状预测提供了条件;而SVM方法适合用于小型训练群体,且通常比传统方法产生更高的预测精度[47],在林木研究领域具有较高的应用潜力。
随着表型组学(phenomics)概念的提出,基于人工智能、计算机视觉、深度学习的精准数据测定技术,将逐渐应用于不同环境、群体、时间点的精确、海量表型数据收集。未来借助航空影像、可移动测定装置等田间表型平台,从空中与近地面等不同空间尺度进行林木冠层结构、生理状态、灾害评估等方面的表型数据收集将成为趋势,获得的大规模精确表型数据将高效用于林木GS研究,破解林木复杂性状测定的“表型瓶颈”,从而实现林业高效管理和适应特定环境林木品种的精准选择。
3.3 联合GWAS和基因组编辑策略提高选育精度和广度
林木基础研究薄弱,大多数控制目标性状的主效基因位点尚未发掘,MAS育种策略尚需增加理论支撑;在此背景下,GS方法为加速林木遗传改良提供了有效方法。然而,GS存在只能选育优异材料却难以创制育种材料的不足,使其在林木复杂性状改良中难以满足定向育种需求。全基因组关联分析(GWAS)方法在解析目标性状的遗传基础、挖掘关键基因变异方面已显示出突出优势。例如,Lamara等[57]联合GWAS和共表达网络分析方法,在白云杉(Picea glauca)中发掘到控制木材硬度、密度、微纤丝角等性状的2 652个候选基因SNP,并确定了MYB和NAC两个主效基因位点[58],系统揭示了木材复杂性状的遗传调控网络。新兴的基因组编辑技术(genome editing),依赖于改造的核酸酶与“分子剪刀”等工具,可实现对特定DNA片段的“编辑”与修饰,从而达到对基因组关键遗传位点的定向精准改造,在林木多性状联合选择研究中具有显著作用。锌指核酸酶、TAL效应核酸酶以及最新开发的规律成簇间隔短回文重复(clustered regularly interspersed short palindromic repeats,CRISPRs)等基因编辑工具,均可精准地靶向基因组内特定的DNA序列,实现了基因片段的重排、敲除、加入或置换[59-62]。因此,利用GS策略开展候选群体目标性状的苗期选择,在缩短育种年限的同时,可高效选育出优良品系个体,以此建立核心育种群体;在此基础上,进一步利用GWAS策略对核心育种群体进行目标性状的加性、显性和上位性遗传效应的联合解析,从而确定目标育种基因,提出优异材料的定向育种方案;最后即可运用CRISPRs编辑技术对目标候选基因进行精准靶向改良修饰,直接创制优异新材料,从分子层面实现林木性状的定向改良与新品种的创制。
在过去的几十年里,林木遗传改良取得了重要进展,特别是某些树种已实现了新品种的稳定选育,显著推动了木本植物育种进程。然而,基于杂交育种和种子园选择的传统育种体系,仍然是林木遗传改良的主要途径;而MAS育种技术提高了杂交和选择的效率,但它在杂合性或自交不亲和性的作物或较长世代的林木育种中的利用仍具有较大的局限性[63]。相比而言,GS的众多优势使其为通过非转基因方法显著加快林木品质遗传改良提供最佳途径,在复杂性状遗传基础薄弱及基因位点难以精准定位的局限下,已成为分子育种的首选策略。随着生物技术与新兴交叉技术的融合发展,尽快建立完善的林木分子设计育种体系,将是林木遗传育种领域亟需解决的重要科学难题。
-
表 1 常用的基因组选择模型
Table 1 Common models for genomic selection
模型
Model基本原理
Basic principle标记效应
Marker effect方差假设
Variance assumptionQTL效应
Effect of
QTLs估计准确度
Estimation accuracy参考文献
Reference最小二乘法
Least square method多元线性回归方程
Multiple linear regression equation固定
Fixed— 高估
Overvalued最低
Minimum[25-26] 最佳线性无偏预测法
Best linear unbiased prediction (RR-BLUP)预测变量的均匀收缩为零允许标记有不均匀效果
Uniform shrinkage of the predictive variable is zero, allowing the marker to have an uneven effect随机
Random相等
Equal低估
Underestimated较高
Higher[3, 25, 27-28] 基因组最佳线性无偏估计
Genomic best linear unbiased prediction (GBLUP)矩阵G代替传统亲缘关系矩阵A
Matrix G replaces the traditional relationship matrix A随机
Random相等
Equal偏高估
Partial overvalued较高
Higher[25-27, 29] 贝叶斯A
Bayes A效应方差的先验和后验均为逆卡方分布,小标记收缩效果为零
Prior and posterior effects of variance are inverse chi-square distribution, and the shrinkage effect of small markers is zero随机
Random所有SNP均有效应
All SNPs have an effect更准确估计
More accurate estimation最高,但低于贝叶斯
Max., but lower than Bayes B[3, 22, 28,30] 贝叶斯B
Bayes B效应方差的先验和后验均为逆卡方分布,收缩和变量选择方法
Prior and posterior effects of variance are inverse chi-square distribution, contraction and variable selection methods随机
Random大多数SNP无效应
Most SNPs have no effect更准确估计
More accurate estimation最高,高于贝叶斯
Max., higher than Bayes B[3, 22, 26, 30] -
[1] Edwards M D, Stuber C W, Wendel J F. Molecular marker-facilitated investigations of quantitative-trait loci in maize(I): numbers, genomic distribution and types of gene action[J]. Genetics, 1987, 116(1): 113−125.
[2] Meuwissen T H E, Hayes B J, Goddard M E. Prediction of total genetic value using genome-wide dense marker maps[J]. Genetics, 2001, 157(4): 1819−1829.
[3] Heslot N, Jannink J L, Sorrells M E. Perspectives for genomic selection applications and research in plants[J]. Crop Science, 2015, 55(1): 1−12. doi: 10.2135/cropsci2014.03.0249.
[4] Hayes B J, Bowman P J, Chamberlain A J, et al. Invited review: genomic selection in dairy cattle: progress and challenges[J]. Journal of Dairy Science, 2009, 92(2): 433−443. doi: 10.3168/jds.2008-1646.
[5] Heffner E L, Lorenz A J, Jannink J L, et al. Plant breeding with genomic selection: gain per unit time and cost[J]. Crop Science, 2010, 50(5): 1681−1690. doi: 10.2135/cropsci2009.11.0662.
[6] Xu Y, Crouch J H. Marker-assisted selection in plant breeding: from publications to practice[J]. Crop Science, 2008, 48(2): 391−407. doi: 10.2135/cropsci2007.04.0191.
[7] Heffner E L, Sorrells M E, Jannink J L. Genomic selection for crop improvement[J]. Crop Science, 2009, 49(1): 1−12. doi: 10.2135/cropsci2008.08.0512.
[8] Grattapaglia D, Resende M D V. Genomic selection in forest tree breeding[J]. Tree Genetics & Genomes, 2011, 7(2): 241−255.
[9] Resende M F R Jr., Munoz P, Acosta J J, et al. Accelerating the domestication of trees using genomic selection: accuracy of prediction models across ages and environments[J]. New Phytologist, 2012, 193(3): 617−624. doi: 10.1111/j.1469-8137.2011.03895.x.
[10] Heffner E L, Jannink J L, Iwata H, et al. Genomic selection accuracy for grain quality traits in biparental wheat populations[J]. Crop Science, 2011, 51(6): 2597−2606. doi: 10.2135/cropsci2011.05.0253.
[11] Lande R, Thompson R. Efficiency of marker assisted selection in the improvement of quantitative traits[J]. Genetics, 1990, 124(3): 743−756.
[12] Souza L, Francisco F, Gonçalves P, et al. Genomic selection in rubber tree breeding: a comparison of models and methods for managing G × E interactions[J/OL]. Frontiers in Plant Science, 2019, 10: 1353 [2020−04−12]. https://www.researchgate.net/ publication/332303864.
[13] Goddard M E, Hayes B J. Genomic selection[J]. Journal of Animal breeding and Genetics, 2007, 124(6): 323−330. doi: 10.1111/j.1439-0388.2007.00702.x.
[14] Lund M S, Sahana G, De Koning D J, et al. Comparison of analyses of the QTLMAS XII common dataset(I): genomic selection[J/OL]. BMC Proceedings, 2009, 3: S1 [2020−04−12]. https://doi.org/10.1186/1753-6561-3-S1-S1.
[15] Whittaker J C, Thompson R, Denham M C. Marker-assisted selection using ridge regression[J]. Genetics Research, 2000, 75(2): 249−252. doi: 10.1017/S0016672399004462.
[16] Clark S A, Hickey J M, Van Der Werf J H J. Different models of genetic variation and their effect on genomic evaluation[J/OL]. Genetics Selection Evolution, 2011, 43(1): 18 [2020−04−12]. https://doi.org/10.1186/1297-9686-43-18.
[17] Legarra A, Christensen O F, Aguilar I, et al. Single step, a general approach for genomic selection[J]. Livestock Science, 2014, 166: 54−65. doi: 10.1016/j.livsci.2014.04.029.
[18] Gao H, Christensen O F, Madsen P, et al. Comparison on genomic predictions using three GBLUP methods and two single-step blending methods in the Nordic holstein population[J/OL]. Genetics Selection Evolution, 2012, 44(1): 8 [2020−04−12]. https://doi.org/10.1186/1297-9686-44-8.
[19] Piepho H P. Ridge regression and extensions for genomewide selection in maize[J]. Crop Science, 2009, 49(4): 1165−1176. doi: 10.2135/cropsci2008.10.0595
[20] Zhong S, Dekkers J C M, Fernando R L, et al. Factors affecting accuracy from genomic selection in populations derived from multiple inbred lines: a barley case study[J]. Genetics, 2009, 182(1): 355−364. doi: 10.1534/genetics.108.098277.
[21] Endelman J B. Ridge regression and other kernels for genomic selection with R package rrBLUP[J]. The Plant Genome, 2011, 4(3): 250−255. doi: 10.3835/plantgenome2011.08.0024.
[22] 王重龙, 丁向东, 刘剑锋, 等. 基因组育种值估计的贝叶斯方法[J]. 遗传, 2014, 36(2):111−118. Wang C L, Ding X D, Liu J F, et al. Bayesian methods for genomic breeding value estimation[J]. Hereditas, 2014, 36(2): 111−118.
[23] Hayes B J, Bowman P J, Chamberlain A C, et al. Accuracy of genomic breeding values in multi-breed dairy cattle populations[J]. Genetics Selection Evolution, 2009, 41(1): 1−9. doi: 10.1186/1297-9686-41-1.
[24] Shikha M, Kanika A, Rao A R, et al. Genomic selection for drought tolerance using genome-wide SNPs in maize[J/OL]. Frontiers in Plant Science, 2017, 8: 550 [2020−04−12]. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5399777/.
[25] 董林松. 通过预选标记法进行基因组选择[D]. 泰安: 山东农业大学, 2012. Dong L S. Genomic selection by pre-selection of markers[D]. Taian: Shandong Agricultural University, 2012.
[26] 林德周. 基因组选择方法及其在水稻杂交种表型预测上的应用研究[D]. 扬州: 扬州大学, 2017. Lin D Z. Study and application of genomic selection for predicting hybrid performance in rice[D]. Yangzhou: Yangzhou University, 2017.
[27] 吴晓平. 基于SNP芯片和全测序数据的奶牛全基因组关联分析和基因组选择研究[D]. 北京: 中国农业大学, 2014. Wu X P. GWAS and genomic prediction based on markers of SNP-Chips and sequence data in dairy cattle populations[D]. Beijing: China Agricultural University, 2014.
[28] 李恒德, 包振民, 孙效文. 基因组选择及其应用[J]. 遗传, 2011, 33(12):1308−1316. Li H D, Bao Z M, Sun X W. Genomic selection and its application[J]. Hereditas, 2011, 33(12): 1308−1316.
[29] Chen L, Li C, Sargolzaei M, et al. Impact of genotype imputation on the performance of GBLUP and Bayesian methods for genomic prediction[J/OL]. PLoS One, 2014, 9(7): e101544 [2020−04−12]. https://doi.org/10.1371/journal.pone.0101544.
[30] Desta Z A, Ortiz R. Genomic selection: genome-wide prediction in plant improvement[J]. Trends in Plant Science, 2014, 19(9): 592−601. doi: 10.1016/j.tplants.2014.05.006.
[31] Eggen A. The development and application of genomic selection as a new breeding paradigm[J]. Animal Frontiers, 2012, 2(1): 10−15. doi: 10.2527/af.2011-0027.
[32] Schaeffer L R. Strategy for applying genome-wide selection in dairy cattle[J]. Journal of Animal Breeding and Genetics, 2006, 123(4): 218−223. doi: 10.1111/j.1439-0388.2006.00595.x.
[33] Lillehammer M, Meuwissen T H E, Sonesson A K. A comparison of dairy cattle breeding designs that use genomic selection[J]. Journal of Dairy Science, 2011, 94(1): 493−500. doi: 10.3168/jds.2010-3518.
[34] Isik F. Genomic selection in forest tree breeding: the concept and an outlook to the future[J]. New Forests, 2014, 45(3): 379−401. doi: 10.1007/s11056-014-9422-z.
[35] Lorenz A, and Smith K. Adding genetically distant individuals to training populations reduces genomic prediction accuracy in barley[J]. Crop Science, 2015, 55(1): 2657−2667.
[36] Beyene Y, Semagn K, Mugo S, et al. Genetic gains in grain yield through genomic selection in eight bi-parental maize populations under drought stress[J]. Crop Science, 2015, 55(1): 154−163. doi: 10.2135/cropsci2014.07.0460.
[37] Spindel J, Begum H, Akdemir D, et al. Genomic selection and association mapping in rice (Oryza sativa): effect of trait genetic architecture, training population composition, marker number and statistical model on accuracy of rice genomic selection in elite, tropical rice breeding lines[J/OL]. PLoS Genetics, 2015, 11(2): e1004982 [2020−04−12]. https://journals.plos.org/plosgenetics/article?id=10.1371/journal.pgen.1004982.
[38] Wu H X, Matheson A C. Genotype by environment interactions in an Australia-wide radiata pine diallel mating experiment: implications for regionalized breeding[J]. Forest Science, 2005, 51(1): 29−40.
[39] Resende M D V, Resende M F R, Sansaloni C P, et al. Genomic selection for growth and wood quality in Eucalyptus: capturing the missing heritability and accelerating breeding for complex traits in forest trees[J]. New Phytologist, 2012, 194(1): 116−128. doi: 10.1111/j.1469-8137.2011.04038.x
[40] Iwata H, Hayashi T, Tsumura Y. Prospects for genomic selection in conifer breeding: a simulation study of Cryptomeria japonica[J]. Tree Genetics & Genomes, 2011, 7(4): 747−758.
[41] Isik F, Bartholomé J, Farjat A, et al. Genomic selection in maritime pine[J]. Plant Science, 2016, 242: 108−119. doi: 10.1016/j.plantsci.2015.08.006.
[42] Li Y, Dunge H. Expected benefit of genomic selection over forward selection in conifer breeding and deployment [J/OL]. PLoS One, 2018, 13(12): e0208232 [2020−04−12]. https://pubmed.ncbi.nlm.nih.gov/30532178/.
[43] Jannink J L, Lorenz A J, Iwata H. Genomic selection in plant breeding: from theory to practice[J]. Briefings in Functional Genomics, 2010, 9(2): 166−177. doi: 10.1093/bfgp/elq001.
[44] Habier D, Fernando R L, Kizilkaya K, et al. Extension of the Bayesian alphabet for genomic selection[J/OL]. BMC Bioinformatics, 2011, 12(1): 186 [2020−04−12]. https://link.springer.com/article/10.1186/1471-2105-12-186.
[45] Harfouche A, Meilan R, Kirst M, et al. Accelerating the domestication of forest trees in a changing world[J]. Trends in Plant Science, 2012, 17(2): 64−72. doi: 10.1016/j.tplants.2011.11.005.
[46] Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521: 436−444. doi: 10.1038/nature14539
[47] Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5−32. doi: 10.1023/A:1010933404324.
[48] Genuer R, Poggi J M, Tuleau-Malot C. Variable selection using random forests[J]. Pattern Recognition Letters, 2010, 31(14): 2225−2236. doi: 10.1016/j.patrec.2010.03.014.
[49] Friedman J H. Stochastic gradient boosting[J]. Computational Statistics & Data Analysis, 2002, 38(4): 367−378.
[50] Freeman E A, Moisen G G, Coulston J W, et al. Random forests and stochastic gradient boosting for predicting tree canopy cover: comparing tuning processes and model performance[J]. Canadian Journal of Forest Research, 2016, 46(3): 323−339. doi: 10.1139/cjfr-2014-0562.
[51] Joachims T. Text categorization with support vector machines: learning with many relevant features[J]. European Conference on Machine Learning, 1998, 1398: 137−142.
[52] Chang C C, Lin C J. LIBSVM: a library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology (TIST), 2011, 2(3): 1−27.
[53] Hsu C W, Lin C J. A comparison of methods for multiclass support vector machines[J]. IEEE Transactions on Neural Networks, 2002, 13(2): 415−425. doi: 10.1109/72.991427.
[54] Mountrakis G, Im J, Ogole C. Support vector machines in remote sensing: a review[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(3): 247−259. doi: 10.1016/j.isprsjprs.2010.11.001.
[55] Ma C, Zhang H H, Wang X. Machine learning for big data analytics in plants[J]. Trends in Plant Science, 2014, 19(12): 798−808. doi: 10.1016/j.tplants.2014.08.004.
[56] Ogutu J O, Piepho H P, Schulz-Streeck T. A comparison of random forests, boosting and support vector machines for genomic selection[J/OL]. BMC Proceedings, 2011, 5(Suppl.3): S11 [2020−05−01]. https://link.springer.com/article/10.1186/1753-6561-5-S3-S11.
[57] Lamara M, Raherison E, Lenz P, et al. Genetic architecture of wood properties based on association analysis and co-expression networks in white spruce[J]. New Phytologist, 2016, 210(1): 240−255. doi: 10.1111/nph.13762.
[58] 尹伟伦, 刘玉军, 刘强. 木本植物基因组研究[J]. 北京林业大学学报, 2002, 24(增刊1):248−253. Yin W L, Liu Y J, Liu Q. Studies on genomes of woody plants[J]. Journal of Beijing Forestry University, 2002, 24(Suppl.1): 248−253.
[59] Azpiroz-Leehan R, Feldmann K A. T-DNA insertion mutagenesis in Arabidopsis: going back and forth[J]. Trends in Genetics, 1997, 13(4): 152−156. doi: 10.1016/S0168-9525(97)01094-9
[60] Ishida Y, Saito H, Ohta S, et al. High efficiency transformation of maize (Zea mays L.) mediated by Agrobacterium tumefaciens[J]. Nature Biotechnology, 1996, 14(6): 745−750. doi: 10.1038/nbt0696-745.
[61] Ainley W M, Sastry-Dent L, Welter M E, et al. Trait stacking via targeted genome editing[J]. Plant Biotechnology Journal, 2013, 11(9): 1126−1134. doi: 10.1111/pbi.12107.
[62] Weeks D P, Spalding M H, Yang B. Use of designer nucleases for targeted gene and genome editing in plants[J]. Plant Biotechnology Journal, 2016, 14(2): 483−495. doi: 10.1111/pbi.12448.
[63] Schaart J G, Van De Wiel C C M, Lotz L A P, et al. Opportunities for products of new plant breeding techniques[J]. Trends in Plant Science, 2016, 21(5): 438−449. doi: 10.1016/j.tplants.2015.11.006.
-
期刊类型引用(1)
1. 徐婷婷,余秋平,漆培艺,刘可慧,李艺,蒋永荣,于方明. 不同淋洗剂对矿区土壤重金属解吸的影响. 广西师范大学学报(自然科学版). 2019(02): 188-193 .  百度学术
百度学术
其他类型引用(1)
计量
- 文章访问数: 2255
- HTML全文浏览量: 707
- PDF下载量: 213
- 被引次数: 2



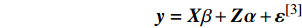
 下载:
下载:
