Effects of thermal treatment temperature and duration on mass loss and rupture modulus of Cunninghamia lanceolata
-
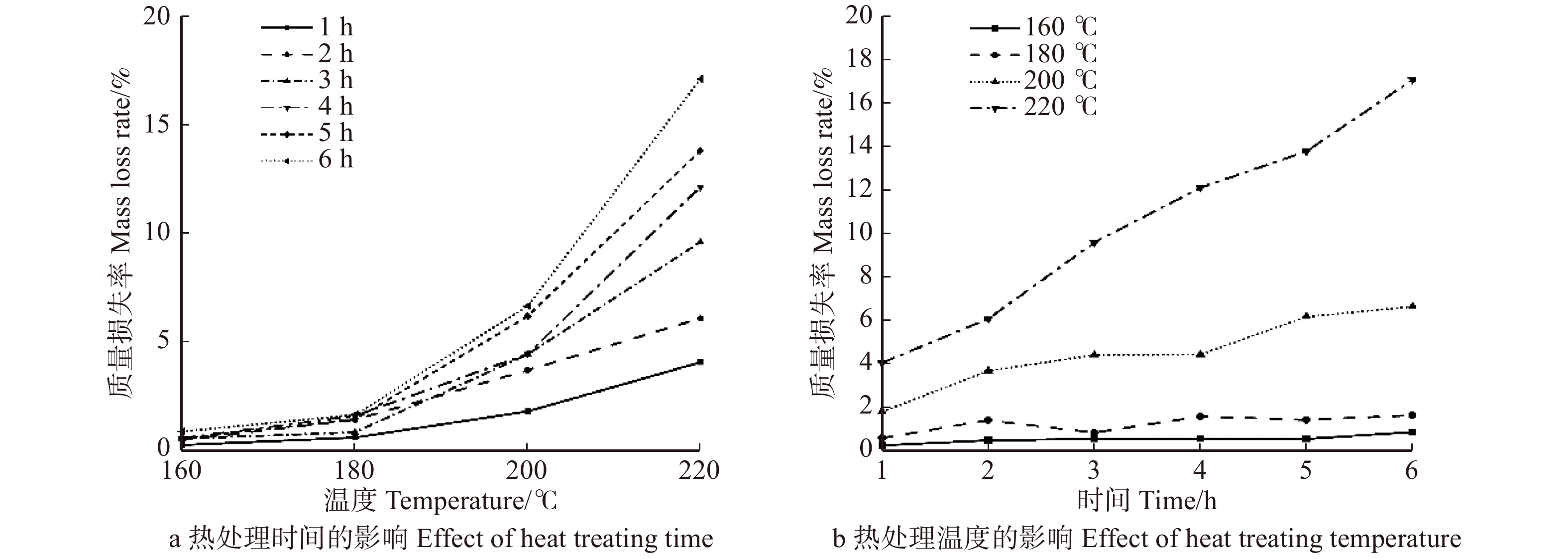
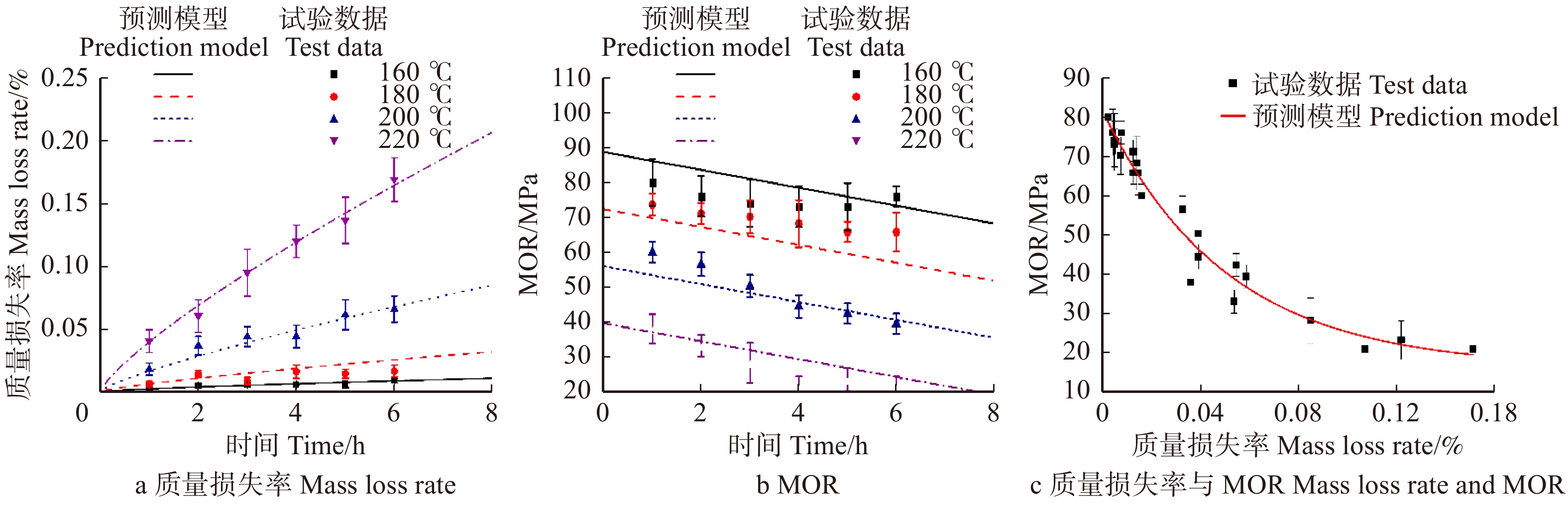
摘要:目的 热处理可以改善木材的尺寸稳定性，同时会降低木材质量并影响木材力学性能，有必要探明热处理对木材质量和力学性能的作用机制。方法 本研究选用人工林杉木薄片作为试验材，在160、180、200、220℃及氮气环境下分别处理1、2、3、4、5、6 h，测试处理后木材的质量损失率（mL）和静曲强度（MOR），采用ATR-FTIR、TGA进行表征，并建立热处理杉木质量损失率和静曲强度的预测模型。结果 热处理温度低于200 ℃时，温度比时间对杉木质量损失率和力学性能的影响更显著。当热处理温度高于200 ℃时，温度和时间对质量损失率和力学性能均有显著性影响。热处理杉木的质量损失率随热处理温度升高和时间延长呈非线性增加，质量损失率范围在0.2% ~ 17.6%之间，其预测模型为lnmL = 0.8lnt + 9.35lnT – 53.67（t为时间，T为温度），R2为0.99，试验测试值与模型预测值基本一致。杉木的MOR随热处理温度升高和热处理时间延长线性降低，与未处理杉木相比，MOR降低了4.4% ~ 74.8%，其预测模型为MOR = −2.57t – 0.82T + 220.44，R2为0.93，该模型总体预测效果较好。热处理杉木MOR随质量损失率增加呈指数下降，两者关系模型为MOR = 65.4
e−20mL + 16.4，R2为0.95，此模型能够预测MOR随质量损失率的非线性变化趋势。结论 通过试验数据建立了杉木的质量损失率与热处理条件，MOR与热处理条件，质量损失率与MOR之间的经验方程，可预测热处理木材质量损失和MOR的变化趋势，为木材热处理工艺的优化和热处理木材性能预测提供参考和依据。Abstract:Objective Heat treatment can improve the dimensional stability of wood, but it will simultaneously reduce its mass and affect its mechanical properties. So it is necessary to explore the mechanism of heat treatment on wood mass and mechanical properties.Method In this study, flakes of Chinese fir plantation were used as the test material, and they were treated at 160, 180, 200, 220 °C and nitrogen atmosphere for 1, 2, 3, 4, 5 and 6 hours, respectively. The mass loss rate (mL) and static bending strength (MOR) of treated wood were tested, characterized by ATR-FTIR and TGA. And the prediction model of mass loss and MOR during heat treating process was established.Result When the heat treating temperature didn’t exceed 200 ℃, it had a more significant impact on the mass loss and mechanical properties of wood than the heat treating time. When the heat treating temperature exceeded 200 °C, heat treating temperature and time had significant effects on wood mass loss and mechanical properties. The mass loss rate of Chinese fir wood showed a non-linear increase with the increase of heat treating temperature and heat treating time, and when the range of mass loss rate was between 0.2% and 17.6%, a model can be established, lnmL = 0.8 lnt + 9.35 lnT – 53.67 (t is time, T is temperature), R2 was 0.99. And the tested values were basically consistent with the predicted values. The MOR of Chinese fir wood decreased linearly with the increase of heat treating temperature and heat treating time. Compared with untreated wood, MOR decreased by 4.4%−74.8%, and a model which had a better forecast can be established, MOR = −2.57t – 0.82T + 220.44, R2 was 0.93. The MOR of heat-treated wood decreased exponentially with the increase of mass loss, and a model that accurately predict the changing trend of MOR with mass loss can be established, MOR = 65.4e−20mL + 16.4, R2 was 0.95.Conclusion This study establishes the empirical equations between mass loss and the heat treating conditions, the MOR and the heat conditions, the mass loss and MOR of Chinese fir wood through the experimental data, which can provide reference and basis for optimization of wood heat treating process and prediction of heat-treated wood performance.-
Keywords:
- heat treatment /
- Chinese fir wood /
- mass loss /
- mechanical property /
- prediction model
-
土壤有机碳（soil organic carbon，SOC）是植物和微生物生长所必需的物质能量来源，是影响土壤肥力、生产力和养分有效性的关键因素，对土壤理化特性具有重要调节作用[1]。SOC储量分布特征是其长期累积的结果，与土壤剖面的发育密切相关。人工林生态系统具有较强的碳汇和增汇潜能[2]，被认为是实现“双碳”目标最经济、最安全的有效途径之一[3]。人工林大面积营建改良了土壤质量，改变了土壤有机质的输入与分解方式，利于SOC贮存和积累[4]，人工林土壤碳库库容较大，能维持较稳定的碳储量[5−6]。然而，人工林SOC的贮存受土壤理化性质、植被类型和地形等诸多因素的影响[7−8]，关于不同人工林下SOC分布特征尚未达成共识。大量研究基于土壤表层或单一林分，吴慧等[9]研究得出热带山地雨林次生林在0 ~ 50 cm垂直方向上土壤有机碳质量分数随土壤深度增加而减小；王越等[10]通过文献整合分析得出油松（Pinus tabuliformis）林0 ~ 20 cm有机碳储量最高，20 ~ 60 cm稳定且保持较低水平；张智勇等[11]认为陕北黄土区沙棘林有机碳储量优于草地和油松林。据《全球森林评估》报道，我国人工林面积居世界前列[12]，人工林生态系统对森林生态系统碳储量增加的贡献较大[13]，因此阐明不同人工林SOC储量的分布特征在宏观方向上研究森林碳汇尤为重要。
黄土高原生境脆弱，水土流失严重。随着“退耕还林还草”生态工程的实施，黄土高原植被覆盖大幅增加[14]，不同人工林土壤固碳问题逐渐成为研究者们关注的热点问题[15]。土地利用变化的改变增强了土壤碳汇功能[16]。Zhang等[17]研究得出退耕后土壤有机碳储量在0 ~ 20 cm以36.67 g/（m2· a）的速率发生巨大的变化，包玉斌[18]研究了2000—2010年陕北黄土高原退耕年间，其退耕地土壤碳固存总量增加。目前，关于黄土高原SOC储量的研究多集中在大尺度空间分布[19]、单一人工林[20]、模型拟合[21]和浅层土壤（0 ~ 100 cm）[11]。这些研究仅是土地利用前后或退耕后单一林地与草地或农田之间的对比研究，而对于退耕后不同人工林及深层土壤SOC储量的研究较少。相关研究表明，土壤是一个不均匀且不连续的时空变异体[22]，其演化过程十分复杂。土壤碳库的分布特征，因缺乏连续、可靠、统一的土壤剖面资料，区域SOC储量实测及代表性数据贫乏[23]，存在明显的不确定性[24]。因此，准确评估退耕后小尺度不同人工林SOC储量的分布特征，对森林土壤有机碳库的精确估算以及土壤碳汇研究具有重要意义。
鉴于此，本研究以黄土丘陵区典型同一退耕年限的人工油松林、山杏（Armeniaca sibirica）林、沙棘（Hippophae rhamnoides）林和天然草地0 ~ 200 cm土壤为研究对象，探究不同人工林SOC储量的垂直分布特征，以期为准确计算黄土高原有机碳储量提供数据支撑，为建立黄土高原土壤碳库，优化人工林土壤固碳格局提供理论依据。
1. 研究区概况与研究方法
1.1 研究区概况
研究区位于陕西省吴起县（107°38′57″ ~ 108°32′49″ E，36°33′33″ ~ 37°24′27″ N），海拔高度1 233 ~ 1 809 m，是典型的黄土高原丘陵沟壑区。吴起县地处中温带半湿润—半干旱区域，温带大陆性季风气候特征明显，年均温7.8 ℃，年平均降水量483.4 mm，时空分布不均，主要集中在7—9月，年无霜期146 d。主要土壤类型为黄绵土，结构疏松、持水力低、易侵蚀。自1999年坡耕地转变为林地以来，形成了刺槐（Robinia pseudoacacia）、油松、侧柏（Platycladus orientalis）、山杏、沙棘、柠条（Caragana sinica）、白莲蒿（Artemisia stechmanniana）、达乌里胡枝子（Lespedeza daurica）等以及自然恢复草地为主的乔灌草植物群落，全县林草覆盖率显著增加，生态环境得以改善。
1.2 土壤样品采集与处理
于2020年9月进行样品采集，在研究区选择相同退耕年限的典型人工油松林、山杏林、沙棘林和天然草地，分别布设25 m × 25 m大样方，利用GPS采集地理信息数据，样地基本信息如表1。使用内径6 cm的土钻，在样方内，采用五点采样法，以0 ~ 20 cm、20 ~ 40 cm、40 ~ 60 cm、60 ~ 100 cm、100 ~ 150 cm、150 ~ 200 cm分层采集土壤样品，带回实验室进行分析。待土壤样品风干后，研磨、过筛，进行理化性质测定。土壤密度采用环刀法测定，土壤有机碳采用重铬酸钾稀释热法测定，全氮采用半微量凯式定氮法测定，全磷采用硫酸−高氯酸消煮−钼锑抗比色法定，全碳通过元素分析仪测定，无机碳根据全碳、有机碳之间关系获得，碱解氮采用碱解扩散法测定，速效磷采用钼锑抗比色法测定，土壤粒度组成使用激光粒度分析仪（Mastersize-zer 3000）测定[25]。
表 1 样地基本信息Table 1. Basic information of the sample plots人工林
Plantation海拔
Elevation/m坡度
Gradient/（°）坡向
Aspect平均高度
Average
height/m平均胸径
Average DBH/cm郁闭度或盖度
Crown density or
coverage林下优势种
Dominant understory
species油松 Pinus tabuliformis 1 362.6 20 SFS 8.5 11.3 0.65 MO, LB, ASB 山杏 Armeniaca sibirica 1 459.7 21 SFS 7.3 10.4 0.62 ASB, PS, LB, PC 沙棘 Hippophae rhamnoides 1 389.9 6 NFS 2.9 3.5 0.71 LS, ASW, LB 草地 Grassland 1 376.7 33 SFS 0.86 LB, LS, SC 注：SFS. 阳坡；NFS. 阴坡；MO. 草木犀；LB. 胡枝子；ASB. 白莲蒿；PS. 败酱；PC. 委陵菜；LS. 赖草；ASW. 猪毛蒿；SC. 针茅。Notes: SFS, south-facing slope; NFS, north-facing slope; MO, Melilotus officinalis; LB, Lespedeza bicolor; ASB, Artemisia stechmanniana; PS, Patrinia scabiosaefolia; PC, Potentilla chinensis; LS, Leymus secalinus; ASW, Artemisia scoparia; SC, Stipa capillata. 土壤有机碳储量计算公式为
SOC储量=wSOCi×ρBDi×Di×0.01 式中：SOC储量表示土壤有机碳储量（g/m2），wSOCi表示第i层的土壤有机碳含量（g/kg），ρBDi表示第i层的土壤密度（g/cm3），Di表示第i层的土层厚度。
1.3 数据处理
应用SPSS26.0对数据进行统计分析，采用单因素方差分析（ANOVA）对比不同人工林、不同土层深度有机碳储量之间的差异；应用Origin2018对土壤有机碳储量与土壤理化性质、不同人工林、地形等影响因素之间的关系强弱和作用机理进行PCA分析并绘图；应用R4.2.1对土壤有机碳储量和各环境变量的贡献关系进行冗余分析。
2. 结果与分析
2.1 有机碳储量分布特征
研究区0 ~ 200 cm土层平均SOC储量由大到小为山杏（16.190 g/m2） > 草地（15.403 g/m2） > 沙棘（11.449 g/m2） > 油松（10.188 g/m2）（表2）。不同人工林SOC储量变异系数在10% ~ 30%，为中等程度变异，表现为沙棘（0.219） > 山杏（0.136） > 油松（0.124） > 草地（0.115）。变异系数表征了SOC储量的空间异质性，沙棘的SOC储量空间异质性最大，草地的SOC储量空间异质性最低。
表 2 不同人工林土壤有机碳储量描述统计Table 2. Description statistical characteristics of soil organic carbon stocks content in different plantations人工林
Plantation土层 Soil
layer/cm平均值
Mean value/（g·m−2）最大值
Max. value/（g·m−2）最小值
Min. value/（g·m−2）标准差
Standard deviation变异系数
Variation coefficient占比
Proportion油松
Pinus tabuliformis0 ~ 20 11.658 12.197 10.627 0.893 0.077 0.191 20 ~ 40 7.009 9.253 4.457 2.412 0.344 0.115 40 ~ 60 7.691 8.506 7.267 0.706 0.092 0.126 60 ~ 100 10.246 12.052 8.016 2.051 0.200 0.167 100 ~ 150 13.491 13.844 13.040 0.411 0.030 0.221 150 ~ 200 11.035 11.050 11.010 0.022 0.002 0.180 0 ~ 200 10.188 13.490 7.008 1.082 0.124 山杏
Armeniaca sibirica0 ~ 20 19.049 20.198 16.988 1.789 0.094 0.196 20 ~ 40 13.201 17.450 10.940 3.683 0.279 0.136 40 ~ 60 11.359 12.901 10.199 1.390 0.122 0.117 60 ~ 100 19.106 23.617 15.815 4.041 0.211 0.197 100 ~ 150 20.097 22.132 19.009 1.764 0.088 0.207 150 ~ 200 14.332 14.670 14.033 0.320 0.022 0.147 0 ~ 200 16.190 20.097 11.359 2.184 0.136 沙棘
Hippophae rhamnoides0 ~ 20 19.692 24.417 16.385 4.199 0.214 0.287 20 ~ 40 9.659 13.084 7.616 2.984 0.309 0.141 40 ~ 60 5.912 8.583 4.269 2.333 0.395 0.086 60 ~ 100 8.850 10.196 7.530 1.333 0.151 0.128 100 ~ 150 13.247 15.749 11.861 2.171 0.164 0.193 150 ~ 200 11.333 12.417 10.544 0.971 0.086 0.165 0 ~ 200 11.449 19.691 5.912 2.331 0.219 草地 Grassland 0 ~ 20 19.906 22.351 16.274 3.208 0.161 0.215 20 ~ 40 10.066 11.177 8.118 1.692 0.168 0.109 40 ~ 60 9.256 10.564 8.160 1.216 0.131 0.100 60 ~ 100 14.409 15.494 12.767 1.446 0.100 0.156 100 ~ 150 20.021 20.836 18.609 1.228 0.061 0.217 150 ~ 200 18.760 20.178 17.629 1.299 0.069 0.203 0 ~ 200 15.403 20.021 9.255 1.681 0.115 在不同人工林中（图1），在0~200 cm剖面上SOC储量呈现出山杏（97.145 g/m2） > 草地（92.418 g/m2） > 沙棘（68.695 g/m2） > 油松（61.130 g/m2）的分布格局，山杏的SOC储量与油松、沙棘差异显著（P < 0.05）。人工油松林，山杏林，沙棘林与天然草地0 ~ 60 cm SOC储量占整个剖面的43.11%、44.89%、51.33%、42.45%，表层碳储量高。垂直分布上，油松、山杏、沙棘的SOC储量自表层向下随深度增加变异系数先增大后减小，在20 ~ 40 cm土层变异系数达到最大，草地的SOC储量自表层向下随深度增加变异系数减小。在不同深度土层中，油松的SOC储量与山杏、沙棘、草地在0 ~ 20 cm、20 ~ 40 cm、150 ~ 200 cm土层差异显著（P < 0.05），沙棘的SOC储量与山杏、油松、草地在40 ~ 60 cm、60 ~ 100 cm土层差异显著（P < 0.05），油松、沙棘的SOC储量与山杏、草地在100 ~ 150 cm土层差异显著（P < 0.05）。
![]()
图 1 不同人工林土壤有机碳储量的垂直分布Figure 1. Vertical distribution of soil organic carbon stocks in different plantations2.2 环境因素对典型人工林土壤有机碳储量的影响
典型人工林SOC储量空间变异的主成分分析如下（图2），第一轴和第二轴解释值分别为39.70%和22.70%。第一主成分与部分环境指标的相关系数在0.37以上，其中，PC1与粉粒、黏粒、坡度正相关，与砂粒负相关，第一主成分主要包含了土壤物理性质信息；第二主成分与部分环境指标的相关系数0.5以上，其中PC2与全碳、碱解氮、全氮正相关，主要包含了土壤化学信息，第一和第二主成分反映的信息量占总信息量的62.40%。
![]()
图 2 土壤有机碳储量与土壤环境因子的主成分分析TP. 全磷；TN. 全氮；TC. 全碳；SIC. 土壤无机碳；AP. 速效磷；AN. 碱解氮；Clay. 黏粒；Silt. 粉粒；Sand. 砂粒；ELE. 海拔；SA. 坡向；SG. 坡度。下同。PC1. 第一主成分；PC2. 第二主成分。TP, total phosphorus; TN, total nitrogen; TC, total carbon; SIC, soil inorganic carbon; AP, available phosphorus; AN, alkali-hydrolyzable nitrogen; Clay, clay; Silt, silt; Sand, sand; ELE, elevation; SA, slope aspect; SG, slope gradient. The same below. PC1, the first principal component; PC2, the second principal component.Figure 2. Principal component analysis of soil organic carbon stocks and soil environmental factors2.3 环境因素对土壤剖面有机碳储量垂直分布的影响
不同环境因素对SOC储量垂直变化的贡献度不同（图3）。土壤化学性质、土壤物理性质、地形和植被群落分别对0 ~ 200 cm土壤剖面中SOC储量分布差异的影响约占51.84%、13.58%、30.71%和3.87%。在土壤化学性质中，0 ~ 200 cm SOC储量的变化受全磷影响最大（11.99%），受全氮影响最小（5.64%）；在土壤物理性质中，0 ~ 200 cm SOC储量的变化受砂粒影响最大（5.65%），受黏粒影响最小（2.89%）；在地形因素中，0 ~ 200 cm SOC储量的变化受海拔影响最大（19.66%），受坡向影响最小（4.97%）；植物群落对0 ~ 200 cm SOC储量变化影响较小。
![]()
图 3 土壤化学性质、土壤物理性质、地形和植物群落对土壤有机碳储量变化的相对贡献SCP. 土壤化学性质；SPP. 土壤物理性质；Topo. 地形；PT. 植物群落。SCP, soil chemical property, SPP, soil physical property, Topo, topography, PT, phytocoenosium.Figure 3. Relative contribution of soil chemistry, soil physical properties, topography and phytocoenosium to changes in soil organic carbon stocks3. 讨 论
3.1 不同人工林土壤有机碳储量分布差异的对比
本研究发现SOC储量富集在土壤表层，呈现出明显的“表聚性”，这与王文静等[26]的研究结论一致。不同植被群落在土壤浅层聚集了大量的根系和凋落物，凋落物分解产生有机质归还于土壤，通过养分的循环进入土壤[27]，因此，大量的有机碳在土壤表层形成和累积。
本研究中，山杏林表现出最优的土壤固碳效益，草地次之，油松林最差，这与李龙波等[28]对乔灌草固碳效益效果的研究结果不一致。植被类型和植被生长间的差异会导致土壤温度、湿度、凋落物数量和根系分泌物等的显著不同[29]，进而影响土壤的固碳效益。本研究中草地植被覆盖度高于油松和沙棘林下植被覆盖度（表1），单位面积的植被残体、根系分泌物、枯枝落叶量多，有机质输入量更高，同时，适宜的土壤温度和湿度促进了微生物的生长代谢，提高了植被残体的分解速率，使得草地土壤固碳效率提高。不同人工林中，植物生产力和质量的巨大差异导致SOC储量空间分布的显著差异[30]。且有研究表明，在年平均降水量 < 510 mm区域，草地比灌木和林地积累更多的有机碳[31]，本研究区位于黄土丘陵区，年降水量483.4 mm，草地SOC储量高于沙棘和油松。落叶乔木在增加枯落物归还量方面明显优于常绿乔木，这在诸多研究中均有报道[32]。本研究中山杏SOC储量远高于油松，是因为落叶阔叶乔木比常绿针叶乔木产生更多的枯落物凋落量[32]，山杏林表层枯落物多，根密度大，不断更替的根系结合不断积累的地表枯落物，不仅改变了土壤腐殖质，也改善了土壤质地，增加了土壤有机碳的积累，因此山杏林具有较高的土壤碳储量，碳汇功能表现较强。
3.2 土壤有机碳储量空间差异的主要影响因素和作用机制
本研究中，不同人工林土壤有机碳储量与黏粒、粉粒和坡度正相关，砂粒与土壤有机碳储量负相关，这阐释了土壤粒径及坡度与土壤有机碳储量之间的关系，这与李顺姬等[33]的研究结果一致。土壤结构是影响有机质分解的主导因素[34]，黏粒对土壤有机碳有很好的保护作用，砂质土壤有机碳的矿化更为迅速[33]。当土壤黏粒含量较高时，具有较大的表面积，易形成较多的毛细管，有较强的毛管作用，完整的土壤孔隙为有机碳自表层向下层传输提供了通道，促进深层土壤有机碳固存[35]，具有较强的固碳能力。而当土壤砂粒含量较高时，有效土层薄，土壤生物作用弱，土壤有机碳矿化作用较弱，微生物群落质量较低，土壤固碳能力较低。黄土丘陵区“退耕还林还草”工程对土壤机械组成产生一定的影响，使土壤物理性质发生变化。土壤机械组成影响土壤孔隙度、密度，改变土壤的透气性和持水能力，改变植物根系的生长发育及微生物活动条件，进而影响有机碳的储存[36]。坡度显著影响土壤有机碳固存，坡度通过影响水分运移、植被分布及土壤机械组成等间接影响土壤有机碳储量。
本研究中，土壤化学性质对SOC储量的影响较大，全氮、碱解氮、全磷对土壤有机碳储量正向效应显著，阐释了土壤有机碳与土壤养分之间的关系。土壤全氮和碱解氮对土壤有机碳的转化和固存有重要作用。全氮对有机碳储量起正向效应，较高的全氮可以降低凋落物中的碳氮比，避免微生物与植物的“争氮”现象，利于凋落物矿化分解[37]，促进土壤有机碳储存。这与王越等[10]研究得出全氮对土壤有机碳呈显著正效应的结果一致。有研究表明，地形显著影响土壤发育、迁移等活动，从而影响土壤碳的输入输出过程[38]。黄土丘陵区水土流失导致了流域内水土资源的重新分配，冗余分析表明，海拔对土壤剖面有机碳储量贮存起主要贡献（图3），通过调控水热条件，进而影响土壤有机碳的积累[39]。
4. 结 论
（1）研究区不同人工林土壤碳储量不同，表现为山杏 > 草地 > 沙棘 > 油松。因此，在黄土高原地区进行人工林营建时，可优先配置山杏林与适宜草种，以增加黄土高原土壤固碳。
（2）研究区不同人工林土壤有机碳储量与土壤机械组成和土壤养分显著相关，黏粒、粉粒、砂粒、全氮、碱解氮是影响黄土丘陵区不同人工林土壤有机碳储量空间分布的主导因子。
（3）研究区人工林土壤有机碳储量在土壤剖面中差异较大，土壤有机碳储量的垂直分布主要受地形的影响。其中，海拔通过影响有机碳的转化与固存对土壤有机碳储量的贮存起主要贡献作用。
-
![]()
图 1 不同热处理温度和时间下的杉木红外光谱图
Figure 1. FTIR spectra of heat-treated Chinese fir wood at different temperatures and times
![]()
图 3 热处理时间和温度对杉木质量损失率的影响
Figure 3. Effects of heat treating time and temperature on the mass loss rate of Chinese fir wood
![]()
图 4 热处理温度和时间对杉木质量损失率和静曲强度的影响
Figure 4. Effects of heat treating conditions on mass loss rate and MOR of Chinese fir wood
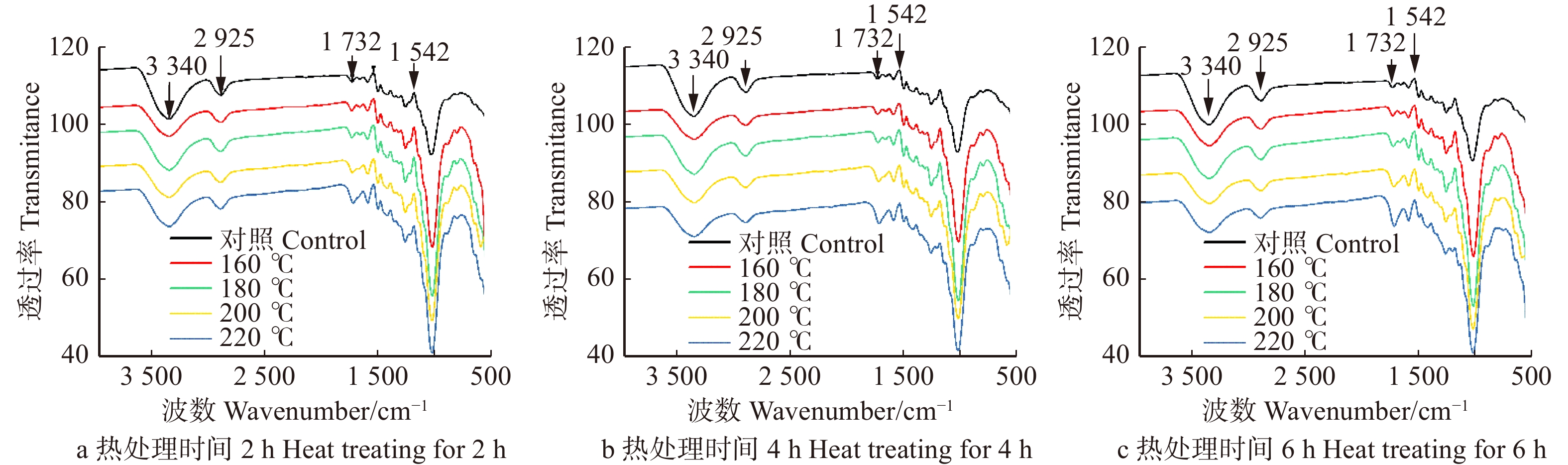
表 1 不同热处理温度和时间条件下杉木的静曲强度
Table 1 MOR of Chinese fir wood under different heat treating temperature and time
MPa 时间 Time/h 温度 Temperature/℃ 160 180 200 220 1 80.1 ± 6.8 73.9 ± 3.2 60.1 ± 2.9 38.1 ± 4.1 2 76.2 ± 5.9 71.3 ± 2.9 56.7 ± 3.4 33.2 ± 3.0 3 74.2 ± 6.8 70.3 ± 4.8 50.4 ± 3.2 28.3 ± 5.8 4 73.3 ± 5.9 68.4 ± 6.7 44.5 ± 3.2 23.5 ± 3.2 5 73.3 ± 6.8 65.9 ± 2.9 42.5 ± 2.9 23.5 ± 3.4 6 76.2 ± 2.9 65.9 ± 5.6 39.6 ± 2.9 21.1 ± 3.2 注：对照的静曲强度为(83.8 ± 3.6) MPa。Note: MOR of the control is (83.8 ± 3.6) MPa. 
下载: 导出CSV
-
[1] 王沈南. 热处理温度对杉木木材性质的影响机制研究[D]. 北京: 中国林业科学研究院, 2017. Wang S N. Impact of different heat treatment temperatures on the properties of Chinese fir wood[D]. Beijing: Chinese Academy of Forestry, 2017.
[2] 江京辉, 吕建雄, 周永东, 等. 水蒸气热处理对人工林杉木性质的影响[J]. 木材工业, 2015, 29(2):13−16. doi: 10.3969/j.issn.1001-8654.2015.02.003. Jiang J H, Lü J X, Zhou Y D, et al. Influence of heat treatment by steam on wood properties of Chinese fir from plantations[J]. China Wood Industry, 2015, 29(2): 13−16. doi: 10.3969/j.issn.1001-8654.2015.02.003.
[3] 丁涛, 蔡家斌, 耿君. 欧洲木材热处理产业和标准化[J]. 木材工业, 2015, 29(3):26−30. Ding T, Cai J B, Geng J. Review on thermally modified timber industry and standardization in Europe[J]. China Wood Industry, 2015, 29(3): 26−30.
[4] Chen Y C, Yang T C, Hung K C, et al. Effects of heat treatment on the chemical compositions and thermal decomposition kinetics of Japanese cedar and beech wood[J]. Polymer Degradation and Stability, 2018, 158: 220−227. doi: 10.1016/j.polymdegradstab.2018.11.003
[5] Esteves B, Pereira H. Wood modification by heat treatment: a review[J]. BioResources, 2008, 4(1): 370−404.
[6] Zaman A, Alen R, Kotilainen R. Thermal behavior of scots pine (Pinus sylvestris) and silver birch (Betula pendula) at 200−230 ℃[J]. Wood & Fiber Science, 2000, 32(2): 138−143.
[7] Yalcin M, Sahin H I. Changes in the chemical structure and decay resistance of heat-treated narrow-leaved ash wood[J]. Maderas: Cienciay Tecnologia, 2015, 17(2): 435−446.
[8] Ozgenc O, Durmaz S, Boyaci I H, et al. Determination of chemical changes in heat-treated wood using ATR-FTIR and FT Raman spectrometry[J]. Spectrochimica Acta Part A-Molecular and Biomolecular Spectroscopy, 2017, 171: 395−400. doi: 10.1016/j.saa.2016.08.026.
[9] 江京辉, 吕建雄. 高温热处理对木材强度影响的研究进展[J]. 南京林业大学学报(自然科学版), 2012, 36(2):1−6. doi: 10.3969/j.issn.1000-2006.2012.02.001. Jiang J H, Lü J X. Research progress in effect of heat treatment on wood strength[J]. Journal of Nanjing Forestry University (Natural Sciences Edition), 2012, 36(2): 1−6. doi: 10.3969/j.issn.1000-2006.2012.02.001.
[10] Bekhta P, Niemz P. Effect of high temperature on the change in color, dimensional stability and mechanical properties of spruce wood[J]. Holzforschung, 2003, 57(5): 539−546. doi: 10.1515/HF.2003.080.
[11] 张乃华, 李康, 李延军, 等. 高温水热处理对马尾松木材物理力学性能的影响[J]. 浙江林业科技, 2017, 37(5):35−41. doi: 10.3969/j.issn.1001-3776.2017.05.006. Zhang N H, Li K, Li Y J, et al. Effect of high temperature hydrothermal treatment on physical and mechanical properties of Pinus massoniana wood[J]. Journal of Zhejiang for Science and Technology, 2017, 37(5): 35−41. doi: 10.3969/j.issn.1001-3776.2017.05.006.
[12] 孙海燕, 苏明垒, 吕建雄, 等. 细胞壁微纤丝角和结晶区对木材物理力学性能影响研究进展[J]. 西北农林科技大学学报(自然科学版), 2019, 47(5):50−58. Sun H Y, Su M L, Lü J X, et al. Research progress on effect of microfibril angel and crystalline area incell wall on wood physical and mechanical properties[J]. Journal of Northwest A&F University (Natural Science Edition), 2019, 47(5): 50−58.
[13] Bergander A, Salmen L. Cell wall properties and their effects on the mechanical properties of fibers[J]. Journal of Materials Science, 2002, 37(1): 151−156. doi: 10.1023/A:1013115925679.
[14] Malek S, Gibson L J. Multi-scale modelling of elastic properties of balsa[J]. International Journal of Solids and Structures, 2017, 113: 118−131.
[15] Tiryaki S, Hamzaçebi C. Predicting modulus of rupture (MOR) and modulus of elasticity (MOE) of heat treated woods by artificial neural networks[J]. Measurement, 2014, 49(1): 266−274.
[16] Čabalová I, Kačík F, Lagaňa R, et al. Effect of thermal treatment on the chemical, physical, and mechanical properties of pedunculate oak (Quercus robur L.) wood[J]. Bioresources, 2018, 13(1): 157−170.
[17] Mburu F, Stephane D, Bocquet J F, et al. Effect of chemical modifications caused by heat treatment on mechanical properties of Grevillea robusta wood[J]. Polymer Degradation & Stability, 2008, 93(2): 401−405.
[18] Zhang N, Xu M, Cai L. Improvement of mechanical, humidity resistance and thermal properties of heat-treated rubber wood by impregnation of SiO2 precursor[J]. Scientific Reports, 2019, 9(1): 982. doi: 10.1038/s41598-018-37363-3.
[19] Shen Y H, Gao Z Z, Hou X F, et al. Spectral and thermal analysis of Eucalyptus wood drying at different temperature and methods[J]. Drying Technology, 2020, 38(3): 313−320. doi: 10.1080/07373937.2019.1566742
[20] Liang T, Wang L. Thermal treatment of poplar hemicelluloses at 180 to 220 ℃ under nitrogen atmosphere[J]. Bioresources, 2016, 12(1): 1128−1135.
[21] Okon K E, Lin F, Chen Y, et al. Effect of silicone oil heat treatment on the chemical composition, cellulose crystalline structure and contact angle of Chinese parasol wood[J]. Carbohydrate Polymers, 2017, 164: 179−185. doi: 10.1016/j.carbpol.2017.01.076.
[22] Popescu C M, Jones D, Krzisnik D, et al. Determination of the effectiveness of a combined thermal/chemical wood modification by the use of FT-IR spectroscopy and chemometric methods [J/OL]. Journal of Molecular Structure, 2020, 1200: 127133 [2020−09−22]. https://doi.org/10.1016/j.molstruc.2019.127133.
[23] Kubovský I, Kačíková D, Kačík F. Structural changes of oak wood main components caused by thermal modification[J/OL]. Polymers, 2020, 12(2): 485 [2020−09−29]. https://doi:10.3390/polym12020485." target="_blank">10.3390/polym12020485">https://doi:10.3390/polym12020485.
[24] Herrera-Diaz R, Sepulveda-Villarroel V, Torres-Mella J, et al. Influence of the wood quality and treatment temperature on the physical and mechanical properties of thermally modified radiata pine[J]. European Journal of Wood and Wood Products, 2019, 77(4): 661−671. doi: 10.1007/s00107-019-01424-9.
[25] Korec R C, Lavri B, Rep G, et al. Thermogravimetry as a possible tool for determining modification degree of thermally treated Norway spruce wood[J]. Journal of Thermal Analysis & Calorimetry, 2009, 98(1): 189−195.
[26] Okon K E, Lin F, Lin X, et al. Modification of Chinese fir (Cunninghamia lanceolata L.) wood by silicone oil heat treatment with micro-wave pretreatment[J]. European Journal of Wood and Wood Products, 2018, 76(1): 221−228. doi: 10.1007/s00107-017-1165-z.
[27] Lee S H, Ashaari Z, Lum W C, et al. Chemical, physico-mechanical properties and biological durability of rubberwood particleboards after post heat-treatment in palm oil[J]. Holzforschung, 2018, 72(2): 159−167. doi: 10.1515/hf-2017-0086.
[28] Fu Z, Zhou Y, Gao X, et al. Changes of water related properties in radiata pine wood due to heat treatment[J/OL]. Construction and Building Materials, 2019, 227: 116692 [2020−09−29]. https://doi.org/10.1016/j.conbuildmat.2019.116692.
[29] Park Y, Jang S K, Park J H, et al. Changes of major chemical components in larch wood through combined treatment of drying and heat treatment using superheated steam[J]. Journal of Wood Science, 2017, 63(6): 635−643. doi: 10.1007/s10086-017-1657-9
[30] 梁铁强, 王立娟. N2中热处理对落叶松木材物理性能的影响[J]. 广东化工, 2016, 43(22):22−23. doi: 10.3969/j.issn.1007-1865.2016.22.010 Liang T Q, Wang L J. The influence of thermal treatment on the physical properties of larch wood under N2 atmosphere[J]. Guangdong Chemical Industry, 2016, 43(22): 22−23. doi: 10.3969/j.issn.1007-1865.2016.22.010
[31] Popescu C, Navi P, Pena M, et al. Structural changes of wood during hydro-thermal and thermal treatments evaluated through NIR spectroscopy and principal component analysis[J]. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2018, 191: 405−412. doi: 10.1016/j.saa.2017.10.045.
[32] Hakkou M, Petrissans M, Zoulalian A, et al. Investigation of wood wettability changes during heat treatment on the basis of chemical analysis[J]. Polymer Degradation and Stability, 2005, 89(1): 1−5. doi: 10.1016/j.polymdegradstab.2004.10.017.
[33] 孔繁旭, 邹超峰, 王艳伟, 等. 热处理对木材化学组分及物理力学性能的影响[J]. 林业机械与木工设备, 2019, 47(1):9−16. doi: 10.3969/j.issn.2095-2953.2019.01.002. Kong F X, Zou C F, Wang Y W, et al. Effect of heat treatment on chemical composition and physico-mechanical properties of wood[J]. Forestry Machinery and Wood working Equipment, 2019, 47(1): 9−16. doi: 10.3969/j.issn.2095-2953.2019.01.002.
[34] Herrera-Diaz R, Sepulveda-Villarroel V, Perez-Pena N, et al. Effect of wood drying and heat modification on some physical and mechanical properties of radiata pine[J]. Drying Technology, 2018, 36(5): 537−544. doi: 10.1080/07373937.2017.1342094.
[35] Kojima E, Yamasaki M, Imaeda K, et al. Effects of thermal modification on the mechanical properties of the wood cell wall of soft wood: behavior of S2 cellulose microfibrils under tensile loading[J]. Journal of Materials Science, 2020, 55(12): 5038−5047. doi: 10.1007/s10853-020-04346-7.
[36] 吴再兴, 陈玉和, 黄成建, 等. 热处理对木材力学性能的影响综述[J]. 世界林业研究, 2019, 32(1):62−67. Wu Z X, Chen Y H, Huang C J, et al. A review of effects of heat treatment on wood mechanical properties[J]. World Forestry Research, 2019, 32(1): 62−67.
[37] Won K R, Hong N E, Park H M, et al. Effects of heating temperature and time on the mechanical properties of heat-treated woods[J]. Journal of the Korean Wood Science and Technology, 2015, 43(2): 168−176. doi: 10.5658/WOOD.2015.43.2.168.
[38] Aydin E, Baysal E, Toker H, et al. Decay resistance, physical, mechanical, and thermal properties of heated oriental beech wood[J]. Wood Research, 2015, 60(6): 913−928.
[39] 黄荣凤, 吕建雄, 曹永建, 等. 高温热处理对毛白杨木材化学成分含量的影响[J]. 北京林业大学学报, 2010, 32(3):155−160. Huang R F, Lü J X, Cao Y J, et al. Impact of heat treatment on chemical composition of Chinese white poplar wood[J]. Journal of Beijing Forestry University, 2010, 32(3): 155−160.
[40] Sebahattin T, Aydın A. An artificial neural network model for predicting compression strength of heat treated woods and comparison with a multiple linear regression model[J]. Construction and Building Materials, 2014, 62: 102−108. doi: 10.1016/j.conbuildmat.2014.03.041.
计量
- 文章访问数: 1428
- HTML全文浏览量: 402
- PDF下载量: 102
