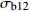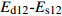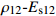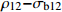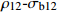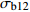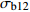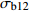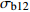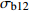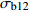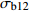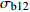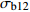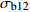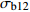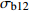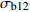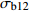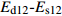辐射松层板抗弯性能的指接参数优化及无损检测研究

叶琦; 管成; 张厚江; 龚迎春; 隋永峰; 刘丽阁

doi:10.12171/j.1000-1522.20210351

辐射松层板抗弯性能的指接参数优化及无损检测研究

叶琦^{1, 2,},
管成^1, ,,
张厚江¹,
龚迎春^2, ,,
隋永峰³,
刘丽阁⁴

1.
北京林业大学工学院，北京 100083
2.
中国林业科学研究院木材工业研究所，北京 100091
3.
靖江国林木业有限公司，江苏靖江 214500
4.
烟台博海木工机械有限公司，山东烟台 264000

基金项目: 国家木竹产业技术创新战略联盟科研计划课题（Tiawbi202001），浙江省省院合作林业科技项目（2021SY09）。

详细信息

作者简介:
叶琦。主要研究方向：无损检测技术。Email：2434956714@qq.com　地址：100083 北京市海淀区清华东路35号北京林业大学工学院

责任作者:
$\fbox{管成}$ ，博士，讲师。主要研究方向：木材无损检测技术。Email：cguan6@bjfu.edu.cn　地址：同上

龚迎春，博士，助理研究员。主要研究方向：木结构力学性能。Email：gongyingchun2015@163.com　地址：100091 北京市海淀区香山路东小府1号中国林业科学研究院木材工业研究所

中图分类号: S781.23；TS653.92
计量
- 文章访问数: 886
- HTML全文浏览量: 293
- PDF下载量: 43
出版历程
- 收稿日期: 2021-09-05
- 修回日期: 2022-01-03
- 录用日期: 2022-01-04
- 网络出版日期: 2022-01-13
- 发布日期: 2022-03-24

Optimization of finger joint parameters and nondestructive testing of bending properties of radiata pine laminates

1.
School of Technology, Beijing Forestry University, Beijing 100083, China
2.
Institute of Wood Industry, Chinese Academy of Forestry, Beijing 100091, China
3.
Jingjiang Guolin Forest Company, Jingjiang 214500, Jiangsu， China
4.
Yantai Bohai Woodworking Machinery Company, Yantai 264000, Shandong, China

摘要

摘要:
目的通过对辐射松层板指接工艺的研究，优化指接过程中的参数，提高指接层板的力学性能；基于应力波方法，开展对指接层板抗弯性能的无损检测研究，提高指接层板的强度稳定性。
方法通过预试验过程确定端压，选择4种不同指长的铣刀，设定3种不同嵌合度大小，研究3因素对指接层板抗弯性能的影响，进而从中选出较优指接参数组合并与标准比对；采用应力波方法检测试件动态弹性模量，并分析密度与动态弹性模量两种无损检测参数与静态弹性模量、抗弯强度两种抗弯性能参数的关系，通过检测层板的密度、动态弹性模量对其抗弯性能进行评估。
结果指接参数对抗弯强度存在较大影响，其中指长与嵌合度对抗弯强度存在一定影响，端压对抗弯强度影响不大；本试验范围内，较优指接参数组合辐射松层板抗弯强度均值可达到29.80 MPa，标准值为20.64 MPa，静态弹性模量为8 533 MPa；试件动态弹性模量与静态弹性模量、抗弯强度和层板密度与静态弹性模量、抗弯强度之间均存在显著相关关系，其中使用动态弹性模量评估层板抗弯性能的预测模型要显著优于基于密度的预测模型。
结论基于端压–位移曲线理论，本研究给出的辐射松结构集成材较优指接参数组合为指长15 mm、齿顶宽0.8 mm、齿底宽0.7 mm、齿根宽3.3 mm、斜度1/12.90、嵌合度0.1 mm、端压11 ~ 17 MPa。基于应力波检测动态弹性模量的方法能够较好地评估指接后辐射松层板的抗弯性能。
- 辐射松 /
- 指接工艺 /
- 弹性模量 /
- 抗弯强度 /
- 无损检测
Abstract:
Objective By the research of finger joint technology of radiated pine laminates, the parameters in finger joint process were optimized and the mechanical properties were improved. Based on the stress wave method, the bending properties of finger joint laminates were studied nondestructively and the strength stability of finger joint laminates was enhanced.
Method The influence of three factors on the laminate mechanical properties was studied with ending pressure determined by pre-experiment process, four milling cutters selected with different finger lengths, three different chimerism degree and finally compared with the standard. The dynamic elastic modulus of the specimens was measured by stress wave method, and the relationship between the two non-destructive testing parameters of density and dynamic elastic modulus and the two bending property parameters of static elastic modulus and bending strength were analyzed. And the bending properties of the laminates were evaluated by testing the density and dynamic modulus of elasticity.
Result The finger joint parameters had great effect on the bending strength. The finger length and chimerism degree had a degree of effect on the bending strength, while the ending pressure had little effect; within the scope of this experiment, the mean value of bending strength of radiata pine laminates with better finger joint parameters could reach 29.80 MPa, while the standard value of bending strength was 20.64 MPa and the static modulus of elasticity was 8 533 MPa; the density and dynamic elastic modulus of the specimens were significantly correlated with the dynamic elastic modulus and bending strength, and the prediction model using dynamic elastic modulus to evaluate the bending properties of the laminates was significantly better than the density-based prediction model.
Conclusion Based on the end-pressure-displacement curve theory, the optimal combination of finger joint parameters for structural glued laminated timber of radiated pine was obtained as follows: finger length 15 mm, tooth tip width 0.8 mm, tooth base width 0.7 mm, tooth root width 3.3 mm, inclination ratio 1/12.90, chimerism degree 0.1 mm, and end pressure 11−17 MPa. The dynamic elastic modulus measurement method based on stress wave can evaluate the bending properties of finger-jointed radiata pine laminates well.
- radiata pine /
- finger joint process /
- modulus of elasticity /
- bending strength /
- nondestructive testing

HTML全文

古筝作为中国传统弹拨乐器的一种，不仅民族文化悠久，演奏的音域还很广泛，这与构成它的部件密不可分，尤其共鸣面板对古筝的发声起了至关重要的作用^[1-2]。古筝共鸣面板的振动性能与众多因素有关，其中共鸣面板的结构是影响其振动性能的重要因素之一。目前很多古筝制造厂多采用拼板与整板两种结构的共鸣面板，拼板结构的面板制作采用折弯工艺，由多块直板胶黏拼接后压弯制成^[3]；整板结构的面板制作采用压弯工艺，将整板烘烤压弯制成。我国民族乐器的发展起源较早，但在对民族乐器共鸣面板及用材性能的评价中，多是通过演奏者或技师的主观评判，这已不适应当前乐器工业发展的需要^[4-5]。随着社会经济的繁荣发展以及民族乐器发展的复杂化，人们对于民族乐器的要求逐渐提高，越来越多的学者对其振动特性进行了研究。

作为力学的一个分支，模态分析技术早已应用于乐器振动研究领域，为乐器声学研究提供了新的技术手段^[6-7]。其主要方法有：（1）计算模态分析，利用有限元分析等现代方法进行力学建模，通过计算机仿真分析得出结果，是借助于计算机的理论分析方法；（2）实验模态分析，使用科学仪器对实物或者模型进行测试，验证理论分析结果，或者直接获得其经验式的力学规律来解决问题。

随着人们对乐器的认识和研究，这类技术被广泛应用。如克拉尼（Chladni）用琴弓摩擦引起薄板振动，从中发现的克拉尼图形成为检验和研究乐器声学效果的有效方法，后来被许多人应用到吉他等其他乐器研究中^[8-10]；通过ANSYS进行仿真，研究琴体的结构或材料对其振动特性的影响，为乐器的设计和制作、音质优化提供了客观依据^[11-13]；共鸣面板作为乐器的关键部件，也常被利用这项技术进行单独研究，对实现生产过程中指导音板结构设计修改及其质量控制具有一定意义^[14-16]；两种模态分析各有优缺点，许多研究将两者结合，通过计算模态分析得到乐器振动特性参数，分析这些参数得出其振动特性，再通过实验模态分析法验证其结果的正确性，为音板声学品质提供了客观评测方法，有利于科学客观的音板声学品质评测系统的研究和建立^[17-19]。目前在乐器声学振动特性领域，大多数学者都是将研究重点放在共鸣面板用小试件上，对整块共鸣面板的分析和评价相对较少。而以整个共鸣面板为研究对象，相对于以梁为研究对象更加贴近古筝共鸣面板的振动形式，使得研究结果更具严谨性。

基于上述分析，本研究以整板结构共鸣面板为研究对象，利用实验模态分析、计算模态分析对共鸣面板的振动特性进行研究，并综合比较实验模态分析与计算模态分析结果，验证计算模态应用于乐器共鸣面板振动特性分析的可行性，以期为整板结构古筝共鸣面板振动性能的研究以及对今后进一步探究不同类型古筝共鸣面板的振动规律提供一定理论依据，对于制造环节与产品声学性能提高也将具有一定意义。

1. 材料与方法

1.1 材　料

本研究选用扬州某企业提供的泡桐制乐器共鸣面板。具体实验对象为泡桐（Paulownia fortunei）制整板结构共鸣面板。其含水率处于12% ~ 14%，密度约等于260 kg/m³，几何参数如表1所示。

表 1 共鸣面板的尺寸规格

Table 1. Geometric parameters of soundboard mm

长度 Length	厚度 Thickness	首部宽度 Head width	尾部宽度 Tail width	宽度方向弧长半径 Arc length radius in width direction	长度方向弧长半径 Arc length radius in length direction
1 630	7	350	295	330	7 300

下载: 导出CSV

| 显示表格

1.2 方　法

1.2.1 实验模态分析

模态是指动力结构的固有振动特性，用固有频率、阻尼系数和固有振型等模态参数来描述。模态分析即结构固有振动特性的分析，目的是为了获得模态参数。实验模态分析法是通过实验采集激励力信号及振动响应信号，经过数据转换，求得频响函数（频响函数是用模态参数来表示）。从求得的频响函数估计出研究对象的模态参数，再对其固有频率、阻尼系数、固有振型等模态参数进行分析得出乐器的固有振动特性。

1.2.2 计算模态分析

有限元法是求解各类工程问题近似解的一种数值计算方法。计算模态分析法是将乐器实体结构离散成互不重叠的有限个微小单元体，其各相邻单元由节点连接。用这些离散的单元集合体的振动特性代替整个音板的振动特性，借助有限元软件ANSYS计算出研究对象的振动特性参数，包括固有频率、阻尼系数、固有振型等，分析这些参数得出乐器的固有振动特性^[18]。

2. 实验模态分析

2.1 实验设置

为了使得到的结果更加接近古筝共鸣面板在实际演奏中的振动，本研究将古筝共鸣面板固定在共鸣箱上，共鸣箱内部框架材料为云杉（ Picea asperata），底板材料为泡桐。经多次预实验后，最终决定将古筝共鸣面板划分为横纹理方向（x方向）6等分，顺纹理方向（y方向）32等分，需要采集信号的总点数为185个。在ZSDASP信号采集分析软件中建立几何结构模拟古筝共鸣面板，并使实际激励点与几何结构上的点相对应。采用ZSL系列冲击力锤逐一敲击试件上的点，通过ZSDASP信号采集分析软件对经ZS7016动态信号采集仪及微型压电式PE加速度传感器采集到的数据进行分析，得到试件传递函数的幅频，最终通过信号处理并选取模态因子函数，得到各阶共振频率及其对应的模态振型^[20-21]，实验设置如图1所示。

图 1 实验模态分析的材料设置方式

Figure 1. Material setup mode of modal analysis experiment

下载: 全尺寸图片幻灯片

2.2 实验模态结果与分析

对古筝共鸣面板进行模态分析后，最终得到各阶次频率及其对应的模态振型图。为便于分析，本研究通过得到的振型图绘制了实验对象振动模态的节线图，如图2所示。

下载: 全尺寸图片幻灯片

图 2 整板结构的古筝共鸣面板的各阶共振频率对应振型图及其振动节线图

Figure 2. Vibration mode diagrams and vibration nodal diagrams corresponding to each order resonant frequency of whole Guzheng soundboard

下载: 全尺寸图片幻灯片

从图2可以得出整板结构共鸣面板的模态振型有如下特点：能够识别到13阶的共振频率与振型，依次为（0,1）、（0,2）、（0,3）、（1,3）、（0,4）、（1,5）、（2,4）、（2,5）、（2,6）、（1,7）、（1,8）、（2,8）、（1,11）阶。其中只沿横纹理方向的弯曲振动阶次为（0,1）、（0,2）、（0,3）、（0,4），在振型上分别表现为有1 ~ 4条顺纹理方向的振动节点线，且振动位移呈顺纹理方向对称。沿顺纹理方向的弯曲振动阶次为（1,n）、（2,n）阶，在振型上分别表现为有1、2条横向的振动节点线。（1,3）、（1,5）、（2,4）、（2,5）、（2,6）、（1,7）、（1,8）、（2,8）、（1,11）阶均为沿顺纹理方向和横纹理方向弯曲振动的叠加，振动形式复杂。另外，从各阶模态振型和振动节线图可以看出，随着阶次的逐渐升高，整板结构共鸣面板的振型也越复杂。同时，得到的振型均匀程度和清晰度也不尽相同，（0,n）阶对应的模态振型相对清晰易识别，（1,n）、（2,n）中的较低阶次，即（1,3）、（1,5）、（2,4）、（2,5）、（2,6）对应的振型识别较为困难。进一步综合分析识别到的整板结构古筝共鸣面板各阶频率的变化趋势，其结果如图3所示。

图 3 整板结构共鸣面板各阶共振频率的变化趋势

Figure 3. Changing trend of resonance frequencies of whole Guzheng soundboard

下载: 全尺寸图片幻灯片

从图3可以得出，各阶次的频率具有如下特点：随着n值的增大，各阶的共振频率逐渐增大。同时，（2,n）阶的共振频率整体高于（1,n）阶，而（1,n）阶的共振频率整体大于（0,n）阶对应的共振频率。

结合之前所得出的特点，随着整板结构共鸣面板沿顺纹理方向和横纹理方向的阶次逐渐升高，对应的共振频率增大，且对应的模态振型均趋于复杂；整板结构共鸣面板的振动阶次多集中在（1,n）和（2,n）阶；从振型上看，整板结构共鸣面板（0,n）阶对应的模态振型相对清晰易识别，（1,n）、（2,n）中的较低阶次对应的振型则不均匀且较难识别。这一方面是由于实验的过程虽尽力营造适合模态分析的最佳条件，但最终的结果仍会受实验环境噪声、人工激励产生误差、边界条件等因素的影响而无法达到完全理想状态，且实验材料本身也并非均质，使得最终得到的模态振型无法达到理想条件下的均匀整齐。另一方面，本研究的对象区别于梁、平板的振动，除了板振动时正常的横纹理方向振动、顺纹理方向振动外，其特定的曲面结构、特殊的边界条件等，都会使其振动更加复杂。这就导致模态分析过程中有的阶次易识别且振型较为明显均匀，有的阶次不易识别，相对应的振型不明显。鉴于本实验个别阶次没有识别到，本研究将从整体上把握整板结构共鸣面板的振动规律和特点，共鸣面板各阶频率之间的具体规律及其具体比例关系需进一步研究得到^[15]。

3. 计算模态分析

借助软件Solidworks 2016和ANSYS14.5对试件进行模拟并对所建模型进行模态分析，并与实验模态分析结果进行对比，验证计算模态分析的可行性。

3.1 共鸣面板模型的建立

本研究省略了顺纹理方向（y方向）的面板弧度，只考虑横纹理方向（x方向）的弧度，同时将面板看成左右同宽的规则结构（俯视图为矩形）。借助SolidWorks软件和通过实际测量获得的几何参数建立了整板结构古筝共鸣面板的三维模型，将模型导入到ANSYS Workbench中进行模态分析，将定义的新材料应用到所建的模型上^[22]。对整板结构共鸣面板模型进行网格划分，共划分了2 144个单元，节点数为15 761个。

3.2 计算模态分析结果及数据分析

根据实验模态分析结果，设定古筝模型的频率范围为0 ~ 1 500 Hz，对整板结构共鸣面板模型进行求解，得到各阶共振频率和模态振型。依据实验获得的阶次范围确定模型的振型阶次。

从图4中的模型结果可以得出，所得振型均随着频率和阶数的升高而变得复杂，这一特点与实验所得结果一致。计算模态分析所得的振型相对实验模态分析所得振型图更均匀且平整。这与诸多因素有关，一方面，计算模态分析时软件会将模型看作是结构均匀致密的材料，不存在孔隙、裂纹或其他缺陷；另一方面，计算模态分析不需要像实验一样从外部采集信号，这样会避免外部环境、人为激励所造成的影响，所得结果较为理想化。

下载: 全尺寸图片幻灯片

图 4 整板结构共鸣面板模型的共振频率和振型

Figure 4. Resonance frequencies and modes of the whole soundboard model

下载: 全尺寸图片幻灯片

3.3 ANSYS模态分析结果与实验所得结果对比分析

对计算模态和实验模态所得阶次对应的频率进行对比并分析，结果如表2、图5所示。

表 2 计算模态分析与实验所得各阶频率对比

Table 2. Frequency comparison between calculated modal analysis and experimental results

阶数 Order	频率 Frequency/Hz		误差 Error/%	阶数 Order	频率 Frequency/Hz		误差 Error/%
阶数 Order	实验结果 Experimental result	计算结果 Calculated result	误差 Error/%	阶数 Order	实验结果 Experimental result	计算结果 Calculated result	误差 Error/%
(0,0)				(1,5)	608.59	608.59	1.17
(0,1)	238.28			(1,6)	764.21	764.21
(0,2)	347.66			(1,7)	910.29	910.29	2.21
(0,3)	425.78			(1,8)	921.97	921.97	1.73
(0,4)	492.19			(1,9)	1 037.00	1 037.00
(0,5)				(1,10)	1 117.20	1 117.20
(0,6)				(1,11)	1 281.00	1 281.00	−0.63
(0,7)				(2,4)	653.58	653.58	−0.41
(0,8)				(2,5)	712.17	712.17	3.00
(0,9)				(2,6)	758.96	758.96	1.72
(0,10)				(2,7)	941.58	941.58
(1,3)	460.94	462.45	0.33	(2,8)	1 032.50	1 032.50	0.50
(1,4)		537.56

下载: 导出CSV

| 显示表格

图 5 整板结构共鸣面板计算模态分析与实验所得各阶次频率变化趋势

Figure 5. Frequency changing trend of each order obtained from the mode analysis and experiment of the whole soundboard

下载: 全尺寸图片幻灯片

从表2可以得出，计算模态分析得到的结果更具连续性，能够识别到选定阶数范围的所有阶次，而实验模态分析时，个别阶数不够明显而识别不到。计算结果中，整板结构共鸣面板模型能够识别到的阶次为（1,n）阶和（2,n）阶，与实验所得结果相比，缺少（0,n）阶，这是由于计算模态分析与实验模态相比存在一定误差。实验模态分析时，共鸣面板被安置在共鸣箱上再进行四周固定；而计算模态分析时为了针对性地分析共鸣面板的各阶次频率及振型，直接对共鸣面板模型进行了四周固定^[15]。

从图5中可以看出，计算模态分析所得各阶频率与实验结果具有相同的变化趋势，各阶频率均随着阶次的升高而逐渐增大，且计算结果与实验结果得到的各阶次对应频率很接近。具体从误差值来看，计算模态分析所得结果除个别阶次外，整体略高于实验模态所得结果。这一方面是由于软件在计算时会将所建模型默认为是材质均匀致密的无缺陷的试件；另一方面，对模型进行前处理时所设置的四周固定边界条件为理想状态，而在实际的实验过程中很难达到理想中的四周完全固定^[23]。但实验对象计算模态分析所得各阶振型对应的频率误差均在5%以内，基于上述分析，可得出该计算模态所得振型及对应频率较为合理，证明了ANSYS模态分析对本研究具有一定可行性。

我国森林资源总量相对不足、质量不高、分布不均，木材市场“需大于供”的状况尚未得到根本改变^[24]。整板结构共鸣面板的原材料相对较少，成本较高，而拼板结构共鸣面板对于木材资源的利用率更高。现如今制筝厂通常采用多种面板拼合的方式制作古筝，不仅提高了制作效率，还能通过无缝拼接使木质更加均匀，统一不同音区的音色^[25]。综上，今后可在本研究基础上进一步探究不同结构共鸣面板的振动特点，为厂家在制造共鸣面板过程中所遇到的问题提供一定的帮助和参考。

4. 结　　论

本研究以整板结构古筝共鸣面板为研究对象，利用ZS7016动态信号采集仪对整板结构共鸣面板进行实验模态分析，得到各阶振动频率及模态振型，从而实现对整板结构共鸣面板声振动特点的分析；并借助软件SolidWorks和ANSYS对共鸣面板建立了三维模型进行计算模态分析，将求解结果与实验模态结果进行对比以探究该方法应用于本研究的可行性，最终得到以下结论：

（1）实验模态分析结果显示：整板结构共鸣面板的振动阶次多为（1,n）和（2,n）阶；（0,n）阶对应的模态振型清晰易识别，而（1,n）、（2,n）中的较低阶次对应的振型识别较为困难。对古筝共鸣面板上的激励点进行信号拾取时，发现拾取难度由筝首到筝尾逐渐降低。

（2）计算模态分析结果显示，整板结构共鸣面板模型能够识别到的阶次为（1,n）阶和（2,n）阶，与实验所得结果相比缺少（0,n）阶。同时，计算模态分析能够识别到选定阶数范围的所有阶，而实验模态分析时个别阶数较难识别。

（3）对比计算模态所得各阶频率，与实验模态结果一致。计算模态分析与实验模态所得各阶频率均随着阶次的升高而逐渐增大，同时共鸣面板所得模态振型均趋于复杂。但计算模态分析的振型更加均匀且理想化。

（4）共鸣面板计算模态分析所得各阶频率整体上比实验模态所得结果略高，但误差均在5%以内，处于合理范围。综合前面得出的结论，计算模态分析应用于本研究具有一定的可行性。

图 1 指接参数示意图

Figure 1. Diagram of finger joint parameters

下载: 全尺寸图片幻灯片

图 2 基于端压–位移曲线理论的预试验验证曲线

Figure 2. Preliminary test verification curves based on the theory of end pressure-displacement curve

下载: 全尺寸图片幻灯片

图 3 应力波无损检测过程示意图

Figure 3. Diagram of stress wave nondestructive testing process

下载: 全尺寸图片幻灯片

图 4 抗弯试验方法示意图

Figure 4. Diagram of bending test method

下载: 全尺寸图片幻灯片

图 5 指接层板抗弯试件破坏模式

Figure 5. Failure modes of bending specimens with finger-jointed laminates

下载: 全尺寸图片幻灯片

图 6 不同指长下试件 $\mathrm{的}{\sigma }_{\mathrm{b}12}$ 均值比较

Figure 6. Comparison of mean values for ${\sigma }_{\mathrm{b}12}$ of specimens with different lengths

下载: 全尺寸图片幻灯片

图 7 不同嵌合度下试件 ${\sigma }_{\mathrm{b}12}$ 均值比较

Figure 7. Comparison of mean values for ${\sigma }_{\mathrm{b}12}$ of specimens with different chimerism

下载: 全尺寸图片幻灯片

图 8 ${E}_{\mathrm{d}12}{{-}}{E}_{\mathrm{s}12}$ 线性拟合曲线

${P}_{x}$ . 拟合变量的P值 P value of fitting variable; ${P}_{{\rm{a}}}$ . 拟合常量的P值 P value of fitting constant; $N$ . 拟合样本个数 The number of fitting specimen.

Figure 8. Linear fitting curve of ${E}_{\mathrm{d}12}{\text{-}}{E}_{\mathrm{s}12}$

下载: 全尺寸图片幻灯片

图 9 ${E}_{\mathrm{d}12}{{-}}{E}_{\mathrm{s}12}$ 均值拟合曲线

Figure 9. Mean fitting curve of ${E}_{\mathrm{d}12}{\text{-}}{E}_{\mathrm{s}12}$

下载: 全尺寸图片幻灯片

图 10 ${E}_{\mathrm{d}12}{{-}}{\sigma }_{\mathrm{b}12}$ 线性拟合对比图

Figure 10. Linear fitting comparison diagram of ${E}_{\mathrm{d}12}{\text{-}}{\sigma }_{\mathrm{b}12}$

下载: 全尺寸图片幻灯片

图 11 $\;{\rho }_{12}{{-}}{E}_{\mathrm{s}12}$ 线性拟合对比图

Figure 11. Linear fitting comparison diagram of $\;{\rho }_{12}{\text{-}}{E}_{{\rm{s}}12}$

下载: 全尺寸图片幻灯片

图 12 $\;{\rho }_{12}{{-}}{\sigma }_{\mathrm{b}12}$ 线性拟合对比图

Figure 12. Linear fitting comparison diagram of $\;{\rho }_{12}{\text{-}}{\sigma }_{\mathrm{b}12}$

下载: 全尺寸图片幻灯片

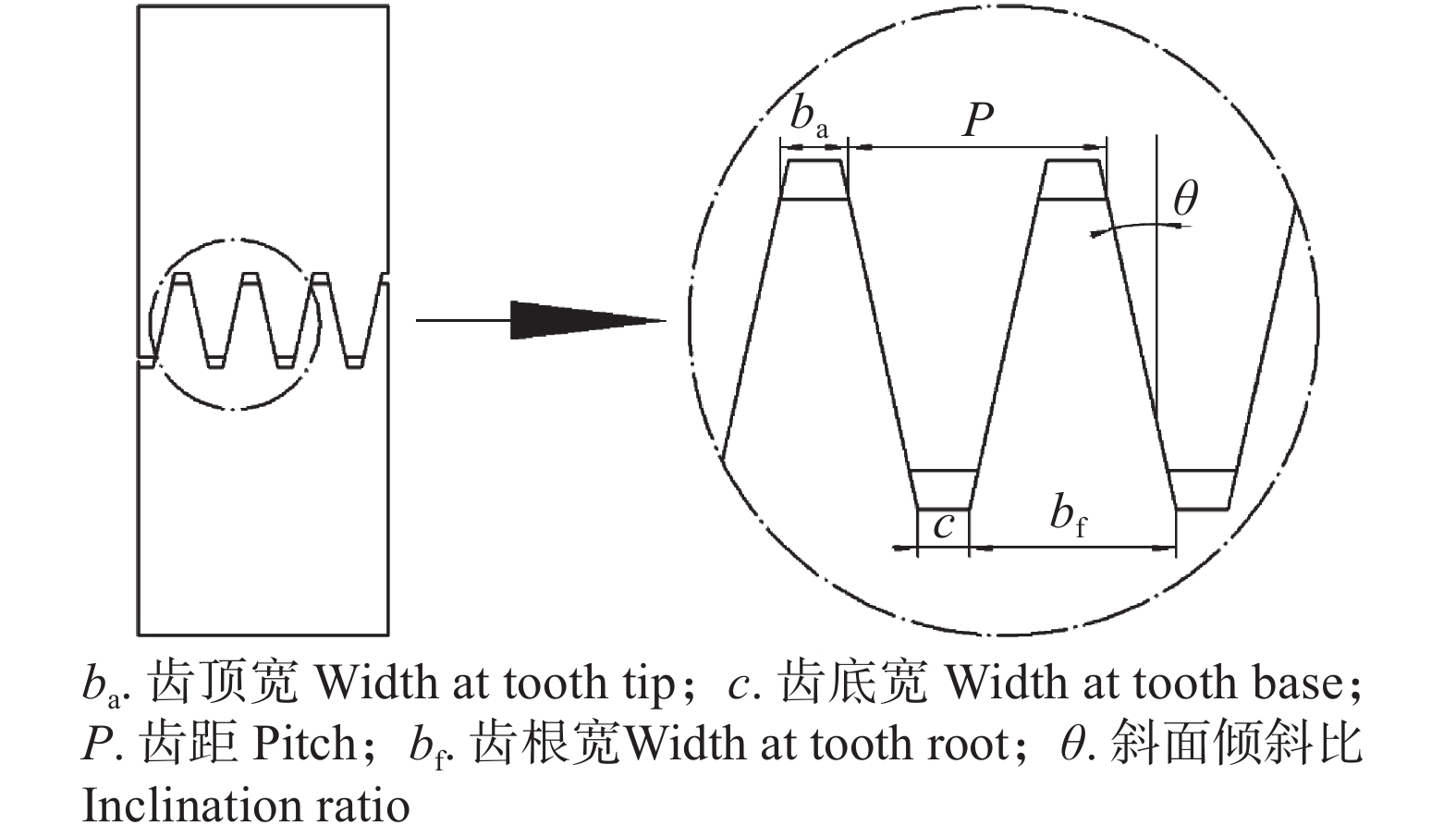
表 1 铣刀参数

Table 1 Parameters of milling cutter

铣刀种类 Type of milling cutter	内径 Diameter inside/mm	外径 Diameter outside/mm	参考指长 Referenced finger length/mm	厚度 Thickness/ mm	刀尖宽度 Tip width/ mm	斜度 Slope
Ⅰ型铣刀 Type Ⅰ milling cutter	50	160	12	4.0	0.6	1/8.87
Ⅱ型铣刀 Type Ⅱ milling cutter	50	160	15	4.0	0.7	1/12.90
Ⅲ型铣刀 Type Ⅲ milling cutter	50	160	19	6.0	1.2	1/10.51
Ⅳ型铣刀 Type Ⅳ milling cutter	50	160	25	7.0	1.2	1/11.27
注：铣刀的斜度数值上表示为刀刃倾斜角度的正切函数值，且与所铣出指榫的斜面倾斜比数值相同。 GB/T 26899—2011《结构用集成材》规定指接材指榫斜面倾斜比应小于1/7.5，内层层板指榫长度不小于10 mm，外层层板指榫长度不小于15 mm，本研究所选铣刀满足要求。Notes: the slope of the milling cutter is shown as the tangent function of the angle of the blade, which is as same as the value of inclination ratio of the finger joint milled by this cutter. GB/T 26899—2011 Structural Glued Laminated Timber stipulated that the inclination ratio of the finger joint shall be less than 1/7.5, the length of the inner layer plate shall be no less than 10 mm, and the length of the outer layer plate shall be no less than 15 mm. The milling cutter selected in this paper meets the requirements.

下载: 导出CSV

表 2 试件指接参数及端压选择

Table 2 Selection of finger joint parameters and end pressure

铣刀种类 Types of milling cutter	嵌合度 Chimerism degree/mm	指榫长度 Finger length/mm	小端压 Small end pressure/MPa	中端压 Medium end pressure/MPa	大端压 Big end pressure/MPa
Ⅰ型铣刀 Type Ⅰ milling cutter	0.1	12.01	13.17	18.27	23.37
	0.2	11.63	11.26	14.86	18.45
	0.3	10.97	10.83	14.40	17.98
Ⅱ型铣刀 Type Ⅱ milling cutter	0.1	16.10	10.94	14.39	17.85
	0.2	15.54	10.10	13.44	16.78
	0.3	14.81	7.54	9.46	11.37
Ⅲ型铣刀 Type Ⅲ milling cutter	0.1	18.40	9.42	12.56	15.70
	0.2	17.90	7.76	9.54	11.31
	0.3	17.30	6.47	7.98	9.50
Ⅳ型铣刀 Type Ⅳ milling cutter	0.1	25.50	9.81	13.45	17.09
	0.2	24.70	8.57	11.20	13.82
	0.3	24.20	5.01	5.84	6.67

下载: 导出CSV

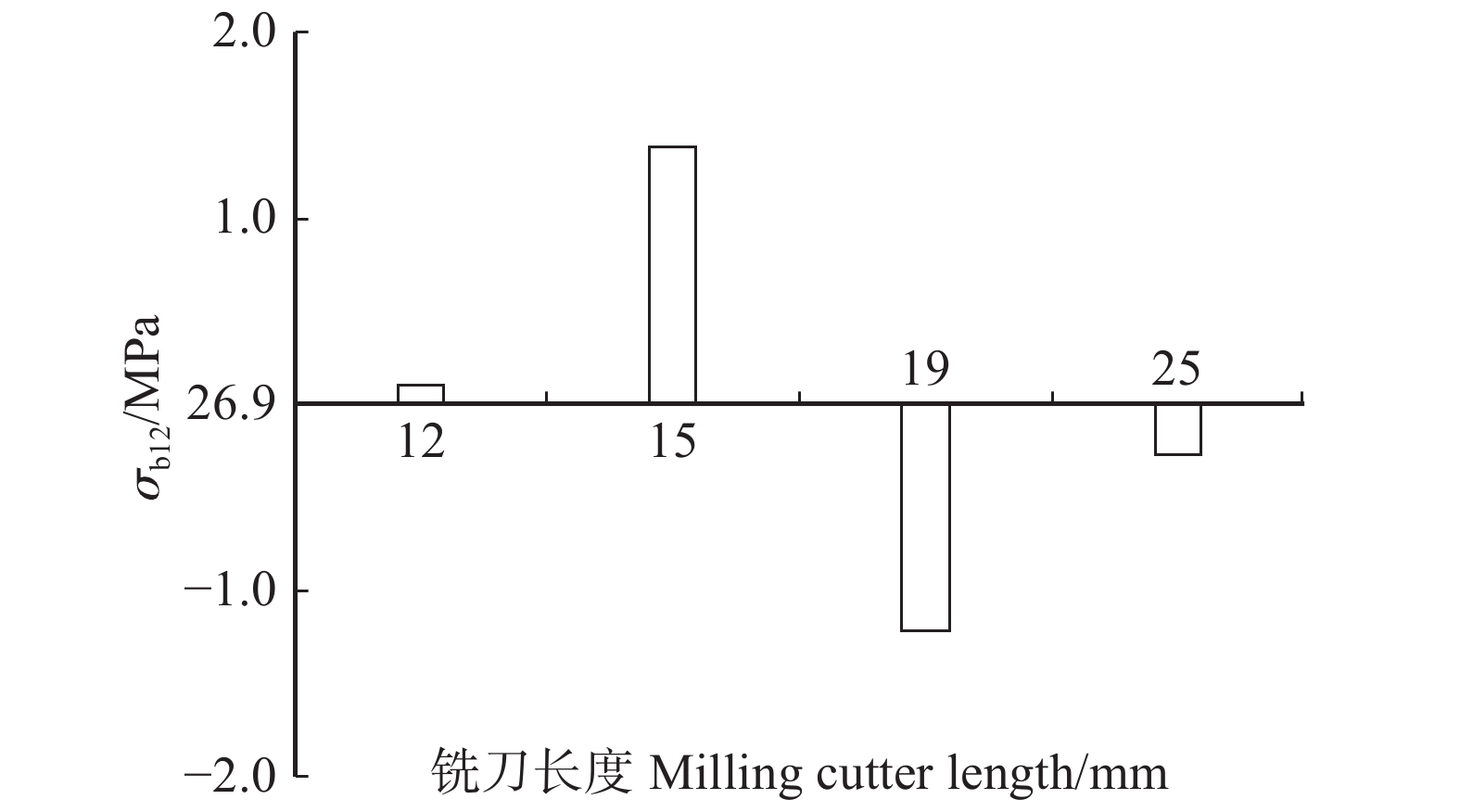
表 3 不同指长组在12%含水率条件下抗弯强度值（ ${\sigma }_{\mathrm{b}12}$ ）的方差齐性检验

Table 3 Homogeneity test of variance for bending strength ( ${\sigma }_{\mathrm{b}12}$ ) under 12% moisture content with different lengths

莱文统计 Levin statistics	df1	df2	P	重复次数 Repeat time
1.669	3	248	0.174	84

下载: 导出CSV

表 4 不同指长组的 ${\sigma }_{\mathrm{b}12}$ 均值差异显著性检验

Table 4 Significance test of mean difference for ${\sigma }_{\mathrm{b}12}$ values with different length

检验方法 Test method	m组指长 Finger length of group m/mm	n组指长 Finger length of group n/mm	${\mathrm{两}\mathrm{组}\sigma }_{\mathrm{b}12}$ 均值差 Numerical difference of mean ${\sigma }_{\mathrm{b}12}$ of the two groups/MPa	P	95%置信区间 95% confidence interval
检验方法 Test method	m组指长 Finger length of group m/mm	n组指长 Finger length of group n/mm		P	置信下限 Confidence lower limit	置信上限 Confidence upper limit
图基 HSD Tukey HSD	12	15	−1.276	0.504	−3.641	1.090
	12	19	1.315	0.477	−1.050	3.680
	12	25	0.376	0.977	−1.990	2.741
	15	19	2.591	0.026*	0.226	4.956
	15	25	1.651	0.273	−0.714	4.016
	19	25	−0.940	0.733	−3.305	1.425
LSD	12	15	−1.276	0.164	−3.077	0.525
	12	19	1.315	0.152	−0.486	3.116
	12	25	0.376	0.682	−1.425	2.177
	15	19	2.591	0.005*	0.790	4.392
	15	25	1.651	0.072	−0.150	3.452
	19	25	−0.940	0.305	−2.741	0.861
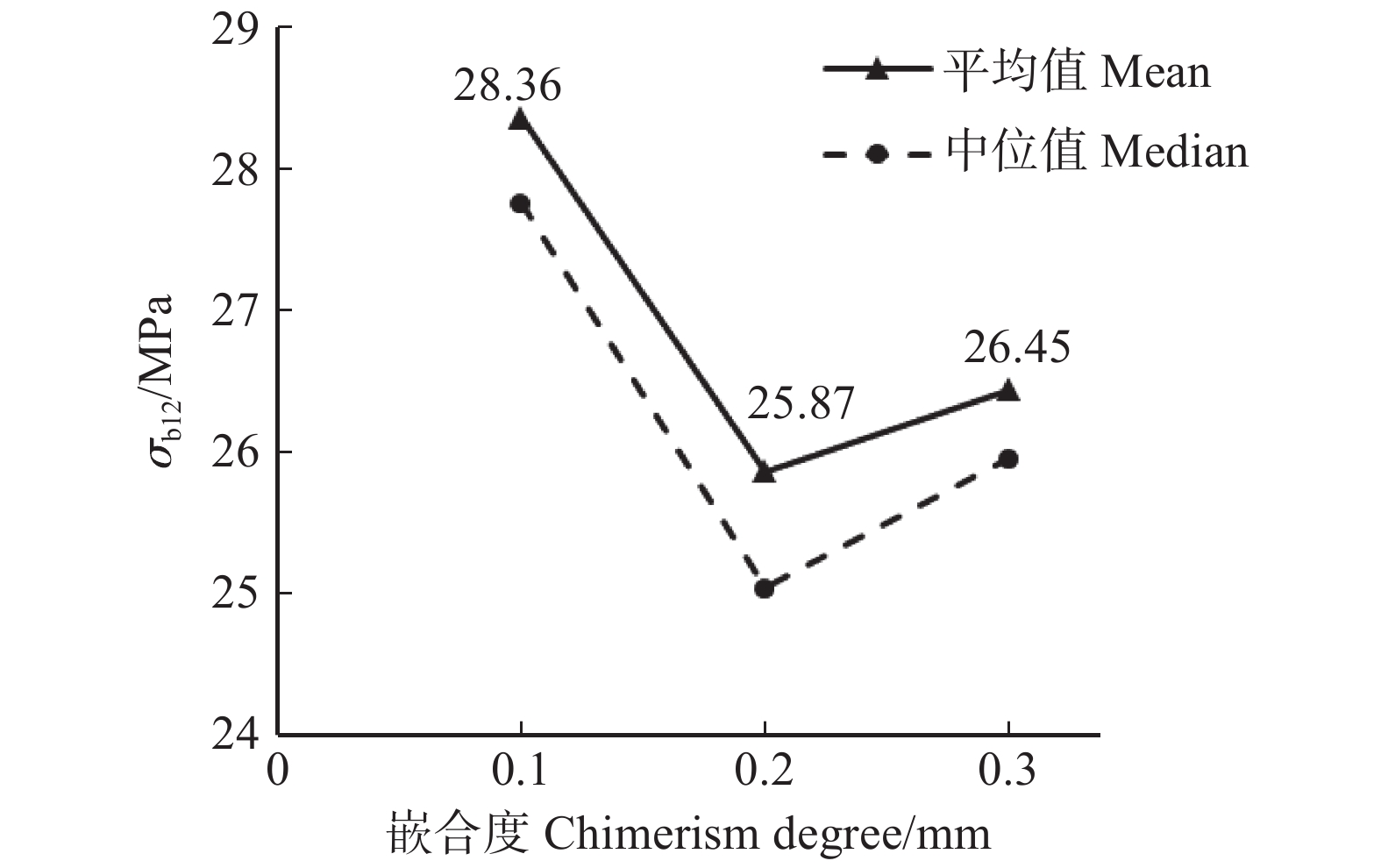
邦弗伦尼 Bonferroni	12	15	−1.276	0.986	−3.708	1.156
	12	19	1.315	0.909	−1.117	3.747
	12	25	0.376	1.000	−2.056	2.807
	15	19	2.591	0.030*	0.159	5.023
	15	25	1.651	0.433	−0.781	4.083
	19	25	−0.940	1.000	−3.372	1.492
注：表示该行两组数据均值在95%置信度下存在显著差异。Note: indicates that there is a significant difference between the mean values of the two groups with 95% confidence.

下载: 导出CSV

表 5 不同嵌合度下 ${\sigma }_{\mathrm{b}12}$ 值的方差齐性检验

Table 5 Homogeneity test of variance for ${\sigma }_{\mathrm{b}12}$ values with different chimerism

莱文统计 Levin statistics	df1	df2	P	重复次数 Repeat time
0.749	2	249	0.474	84

下载: 导出CSV

表 6 不同嵌合度下 ${\sigma }_{\mathrm{b}12}$ 均值差异显著性检验

Table 6 Significance test of mean difference for ${\sigma }_{\mathrm{b}12}$ values with different chimerism

检验方法 Test method	m组嵌合度 Chimerism degree of group m/mm	n组嵌合度 Chimerism degree of group n/mm	${\mathrm{两}\mathrm{组}\sigma }_{\mathrm{b}12}$ 均值差 Numerical difference of mean ${\sigma }_{\mathrm{b}12}$ of the two groups /MPa	P	95%置信区间 95% confidence interval
检验方法 Test method	m组嵌合度 Chimerism degree of group m/mm	n组嵌合度 Chimerism degree of group n/mm		P	置信下限 Confidence lower limit	置信上限 Confidence upper limit
图基HSD Tukey HSD	0.1	0.2	2.481	0.005*	0.627	4.335
	0.1	0.3	1.905	0.042*	0.051	3.759
	0.2	0.3	−0.576	0.744	−2.430	1.278
LSD	0.1	0.2	2.481	0.002*	0.933	4.030
	0.1	0.3	1.905	0.016*	0.357	3.454
	0.2	0.3	−0.576	0.465	−2.125	0.973
邦弗伦尼 Bonferroni	0.1	0.2	2.481	0.005*	0.586	4.376
	0.1	0.3	1.905	0.048*	0.010	3.801
	0.2	0.3	−0.576	1.000	−2.471	1.319

下载: 导出CSV

表 7 不同端压组下 ${\sigma }_{\mathrm{b}12}$ 值描述性统计

Table 7 Descriptive statistics of ${\sigma }_{\mathrm{b}12}$ values in different end pressure groups

组别 Group	样本数 Sample number	均值 Mean/MPa	标准差 Standard deviation/MPa	变异系数 Variation coefficient/%	最小值 Min. value/MPa	最大值 Max. value/MPa
小端压 Small end pressure	84	27.66	4.965	17.95	16.56	39.61
中端压 Medial end pressure	84	26.10	5.006	19.18	14.96	41.53
大端压 Large end pressure	84	26.92	5.509	20.47	13.02	39.93
总计 Total	252	26.89	5.185	19.28	13.02	41.53

下载: 导出CSV

表 8 不同端压组下 ${\sigma }_{\mathrm{b}12}$ 值的方差齐性检验

Table 8 Homogeneity test of variance for ${\sigma }_{\mathrm{b}12}$ under different end pressure

莱文统计 Levin statistics	df1	df2	P	重复次数 Repeat time
0.803	2	249	0.449	84

下载: 导出CSV

表 9 不同端压组的 ${\sigma }_{\mathrm{b}12}$ 均值差异显著性检验

Table 9 Significance test of mean difference for ${\sigma }_{\mathrm{b}12}$ values with different end pressure

检验方法 Test method	m组端压 End pressure of group m	n组端压 End pressure of group n	${\mathrm{两}\mathrm{组}\sigma }_{\mathrm{b}12}$ 均值差 Numerical difference of mean ${\sigma }_{\mathrm{b}12}$ of the two groups/MPa	P	95%置信区间 95% confidence interval
检验方法 Test method	m组端压 End pressure of group m	n组端压 End pressure of group n		P	置信下限 Confidence lower limit	置信上限 Confidence upper limit
图基 HSD Tukey HSD	小 Small	中 Medial	1.565	0.124	−0.315	3.445
	小 Small	大 Large	0.747	0.617	−1.133	2.627
	中 Medial	大 Large	−0.818	0.561	−2.698	1.062
LSD	小 Small	中 Medial	1.565	0.051	−0.005	3.135
	小 Small	大 Large	0.747	0.350	−0.823	2.317
	中 Medial	大 Large	−0.818	0.306	−2.388	0.752
邦弗伦尼 Bonferroni	小 Small	中 Medial	1.565	0.152	−0.356	3.486
	小 Small	大 Large	0.747	1.000	−1.174	2.668
	中 Medial	大 Large	−0.818	0.918	−2.739	1.103

下载: 导出CSV

表 10 指接层板性能参数均值简化

Table 10 Simplified mean performance parameters of finger joint laminates

指长 Finger length/mm	嵌合度 Chimerism degree/mm	${\rho }_{12}$ / (g·cm⁻³)	${E}_{\mathrm{d}12}$ / GPa	${E}_{\mathrm{s}12}$ / GPa	${\sigma }_{\mathrm{b}12}$ / MPa
12	0.1	0.466	7.032	8.266^a	30.409^a
	0.2	0.445	6.236	7.021	26.831
	0.3	0.452	5.363	7.542	23.752
15	0.1	0.449	7.032	8.533^b	29.803^b
	0.2	0.449	6.204	7.351	26.532
	0.3	0.463	7.251	8.693^c	28.485^c
19	0.1	0.452	6.356	7.486	26.165
	0.2	0.448	6.283	7.953	24.847
	0.3	0.431	5.628	6.842	26.034
25	0.1	0.434	5.664	6.638	27.046
	0.2	0.438	6.206	7.509	25.288
	0.3	0.461	6.835	7.697	27.531
注： $\; {\rho }_{12}$ 、 ${E}_{\mathrm{d}12}$ 、 ${E}_{\mathrm{s}12}$ 和 ${\sigma }_{\mathrm{b}12}$ 分别为层板在12%含水率条件下的密度、动态弹性模量、静态弹性模量和抗弯强度。取本试验范围内力学性能最好的3组指接参数组合，分别标记为a组、b组、c组。抗弯强度：a组 > b组 > c组；静态弹性模量：c组 > b组 > a组。Notes: $\; {\rho }_{12}$ , ${E}_{\mathrm{d}12}$ , ${E}_{\mathrm{s}12}$ and ${\sigma }_{\mathrm{b}12}$ are the density, dynamic elastic modulus, static elastic modulus and bending strength of laminates under 12% moisture content. The three groups of finger joint parameter combinations with the best mechanical property within the test range are labeled as group a, group b and group c, respectively. In bending strength, group a >group b > group c; in static modulus of elasticity, group c > group b> group a.

下载: 导出CSV

表 11 性能参数分布模型拟合

Table 11 Performance parameter distribution model fitting

概率密度函数 Probability density function		正态分布 Normal distribution	对数正态分布 Lognormal distribution	威布尔分布 Weibull distribution	95%置信度临界值 Critical value of 95% confidence
概率密度函数 Probability density function		$f\left(x\right)=\dfrac{1}{\beta \sqrt{2\text{π }}}{{\rm{e}}}^{-\frac{{\left(x-\alpha \right)}^{2}}{2{\beta }^{2}}}$	$f\left(x\right)=\dfrac{1}{x\beta \sqrt{2\text{π }}}{{\rm{e}}}^{-\frac{{\left(\mathrm{l}\mathrm{n}x-\alpha \right)}^{2}}{2{\beta }^{2}}}$	$f\left(x\right)=\dfrac{\beta {x}^{\beta -1}}{{\alpha }^{\beta }}{{\rm{e}}}^{-{\left(\frac{x}{\alpha }\right)}^{\beta }}$	95%置信度临界值 Critical value of 95% confidence
$\;\rho$	$\alpha$	0.449	−0.803	0.464
	$\;\beta$	0.0352	0.0780	15.4860
	K-S检验 K-S test	0.0359	0.0335	0.0814	0.0857
${E}_{\mathrm{d}}$	$\alpha$	6.341	1.827	6.822
	$\;\beta$	1.275	0.201	6.164
	K-S检验K-S test	0.0664	0.0303	0.0969	0.0857
${E}_{\mathrm{s}}$	$\alpha$	7.628	2.011	8.215
	$\;\beta$	1.564	0.205	6.041
	K-S检验K-S test	0.0511	0.0334	0.0731	0.0857
${\sigma }_{\mathrm{b}}$	$\alpha$	26.894	3.273	28.887
	$\;\beta$	5.185	0.195	6.365
	K-S检验K-S test	0.0642	0.0464	0.0951	0.0857
注： $\;\rho$ 、 ${E}_{\mathrm{d}}$ 、 ${E}_{\mathrm{s}}$ 和 ${\sigma }_{\mathrm{b}}$ 分别为层板的密度、动态弹性模量、静态弹性模量和抗弯强度； $\alpha$ 和 $\;\beta$ 为概率密度函数公式中的对应参数。Notes： $\;\rho$ , ${E}_{\mathrm{d}}$ , ${E}_{\mathrm{s}}$ and ${\sigma }_{\mathrm{b}}$ are the density, dynamic elastic modulus, static elastic modulus and bending strength of laminates; $\alpha$ and $\;\beta$ are the corresponding parameters in formulae of probability density function.

下载: 导出CSV

表 12 不同指接参数组合下试件力学性能参数

Table 12 Mechanical performance parameters of specimens under different finger joint parameter combinations MPa

指接参数组合 Finger joint parameter combination	${E}_{\mathrm{s}12}$ 均值 Mean of ${E}_{\mathrm{s}12}$	${\sigma }_{\mathrm{b}12}$ 均值 Mean of ${\sigma }_{\mathrm{b}12}$	${\sigma }_{\mathrm{b}12}$ 标准值 Standard value of ${\sigma }_{\mathrm{b}12}$
指接参数组合 Finger joint parameter combination	${E}_{\mathrm{s}12}$ 均值 Mean of ${E}_{\mathrm{s}12}$		参数法–正态分布 Parametric method-normal distribution	参数法–对数正态 Parametric method-lognormal distribution	非参数法 Nonparametric method
a组 Group a	8 266	30.41	20.39	21.62	20.90
b组 Group b	8 533	29.80	20.31	21.29	19.98
c组 Group c	8 693	28.49	17.94	19.07	18.40
总体 Total	7 628	26.89	18.01	18.90	19.55

下载: 导出CSV

表 13 4项指标的双变量相关性检验

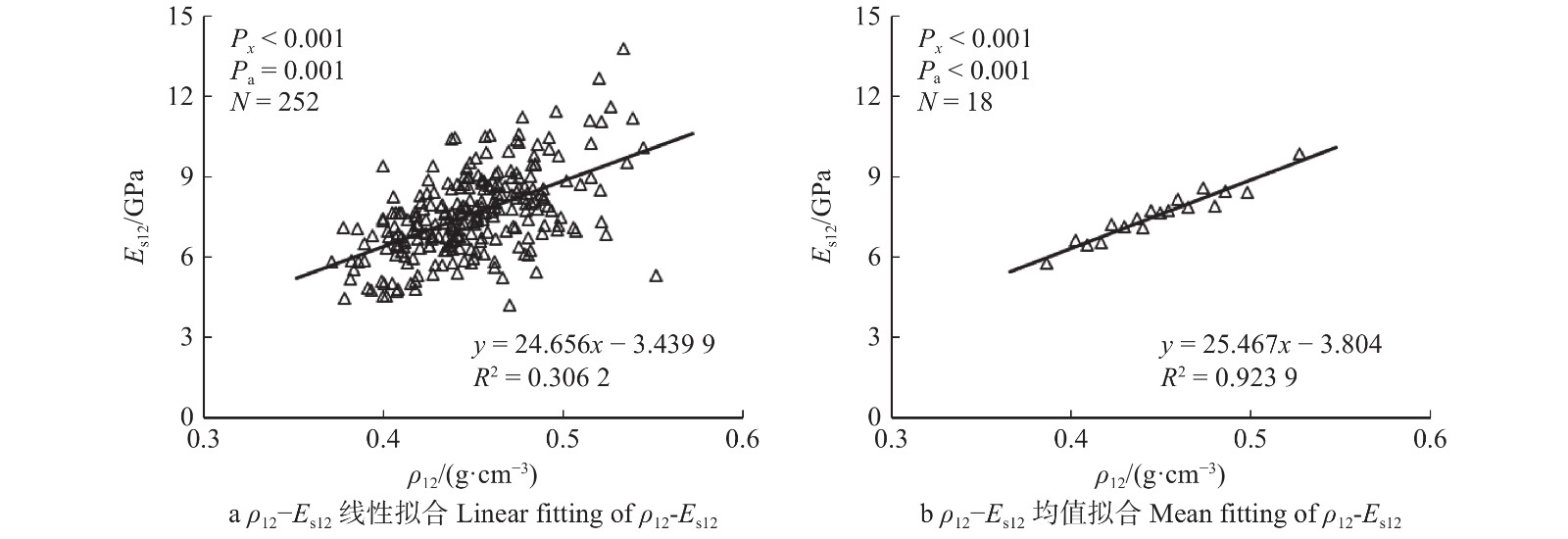
Table 13 Bivariate correlation test of four indicators

检验变量 Test variable	检验参数 Test parameter	${E}_{\mathrm{s}12}$	${\sigma }_{\mathrm{b}12}$
${E}_{\mathrm{d}12}$	皮尔逊系数 Pearson coefficient	0.886^**	0.603^**
${E}_{\mathrm{d}12}$	P	< 0.001	< 0.001
${\rho }_{12}$	皮尔逊系数 Pearson coefficient	0.553^**	0.448^**
${\rho }_{12}$	P	< 0.001	< 0.001
注： ^表示在99%置信度（双尾）条件下，相关性显著。Notes: ^ means the correlation is significant under 99% confidence (two tails) condition.

下载: 导出CSV

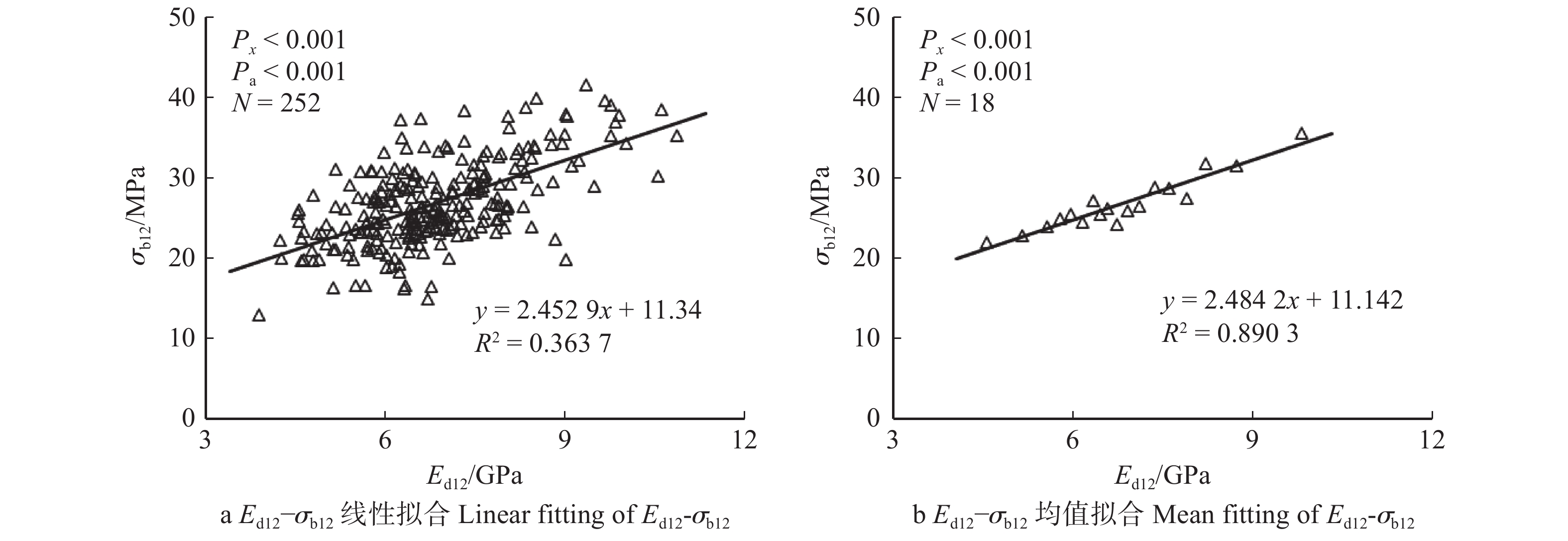
表 14 不同指接参数组合的 ${E}_{\mathrm{d}12}{{-}}{E}_{\mathrm{s}12}$ 拟合曲线参数及显著性检验

Table 14 Fitting curve parameters and significance test of ${E}_{\mathrm{d}12}{\text{-}}{E}_{\mathrm{s}12}$ with different joint parameter combinations

指长 Finger length/mm	嵌合度 Chimerism degree/mm	变量系数 Coefficient of variation	标准差 Standard deviation	${P}_{x}$ 值 ${P}_{x}$ value	常数项 Constant term	标准差 Standard deviation	${P}_{{\rm{a}}}$ 值 ${P}_{{\rm{a}}}$ value
12	0.1	1.120	0.132	0.806^x*	0.394	0.938	0.719^a*
	0.2	0.880	0.096	0.045^x*	1.532	0.613	0.210^a*
	0.3	1.279	0.147	0.206^x*	0.680	0.801	0.945^a*
15	0.1	1.118	0.077	0.689^x*	0.671	0.548	0.907^a*
	0.2	1.134	0.077	0.546^x*	0.314	0.488	0.398^a*
	0.3	1.322	0.125	0.077^x*	−0.890	0.925	0.095^a*
19	0.1	1.212	0.107	0.255^x*	−0.220	0.691	0.183^a*
	0.2	1.335	0.118	0.048^x*	−0.437	0.749	0.134^a*
	0.3	1.283	0.148	0.200^x*	−0.378	0.843	0.202^a*
25	0.1	1.138	0.112	0.653^x*	0.192	0.644	0.409^a*
	0.2	1.394	0.193	0.127^x*	−1.143	1.208	0.136^a*
	0.3	0.799	0.110	0.017^x*	2.235	0.763	0.065^a*
注： x为不同指接参数组变量系数与整体变量系数1.087之间的差异显著性；a为不同指接参数组常数项与整体常数项0.737之间的差异显著性。Notes: x* means the degree of difference between the variable coefficient of different joint parameter groups and the global variable coefficient 1.087; a* means the degree of difference between the constant term of different joint parameter groups and the global constant term 0.737.

下载: 导出CSV

参考文献(23)

[1]	付宗营, 周凡, 高鑫,等. 热处理对进口辐射松木材抗弯性能和尺寸稳定性的影响[J]. 木材工业, 2019, 33(6): 47−50. Fu Z Y, Zhou F, Gao X, et al. Heat treatment effect on bending properties and dimensional stability of imported radiata pine wood[J]. China Wood Industry, 2019, 33(6): 47−50.
[2]	杨丽虎, 杨松, 魏立婷,等. 改性辐射松木材物理力学性能研究[J]. 林产工业, 2019, 46(5): 32−36. Yang L H, Yang S, Wei L T, et al. Study on physical and mechanical properties of radiata pine[J]. China Forest Products Industry, 2019, 46(5): 32−36.
[3]	René H D, Víctor S V, José T M, et al. Influence of the wood quality and treatment temperature on the physical and mechanical properties of thermally modified radiata pine[J]. European Journal of Wood and Wood Products, 2019, 77(4): 661−671. doi: 10.1007/s00107-019-01424-9
[4]	刘培培. 不同化学改性对辐射松及毛竹的霉变性能研究[D]. 哈尔滨: 东北林业大学, 2017. Liu P P. Study on the mildew resistance of chemically modified radiata pine and Moso bamboo[D]. Harbin: Northeast Forestry University, 2017.
[5]	中华人民共和国住房和城乡建设部. 木结构设计标准: GB 50005—2017 [S]. 北京: 中国建筑工业出版社, 2018. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard for design of structure timbers: GB 50005–2017 [S]. Beijing: China Architecture & Building Press, 2018.
[6]	Ayarkwa J, Hirashima Y, Sasaki Y, et al. Influence of finger-joint geometry and end pressure on tensile properties of three finger-jointed tropical African hardwoods[J]. Southern African Forestry Journal, 2000, 188(1): 37−49. doi: 10.1080/10295925.2000.9631268
[7]	谢力生, 刘佳权, 乔鹭婷, 等. 结构用集成材落叶松层板指接工艺[J]. 林业科学, 2016, 52(9): 107−112. Xie L S, Liu J Q, Qiao L T, et al. Finger-jointing technique of larch structural glued laminated timber[J]. Scientia Silvae Sinicae, 2016, 52(9): 107−112.
[8]	堀江秀夫, 合田久敬. 构造用指接集成材的强度性能[J]. 林产试研报, 1986(75): 45−47. Horie H, Kurata H. Strength properties of structural finger-jointed lumber[J]. Report of the Hokkaido Forest Products Research Institute, 1986(75): 45−47.
[9]	林兰英, 傅峰. 短榫指接端压和嵌合度参数分析[J]. 北京林业大学学报, 2008, 30(2): 138−142. doi: 10.3321/j.issn:1000-1522.2008.02.024 Lin L Y, Fu F. End pressure and fitness ratio for mini-finger jointing[J]. Journal of Beijing Forestry University, 2008, 30(2): 138−142. doi: 10.3321/j.issn:1000-1522.2008.02.024
[10]	林兰英, 傅峰. 人工林桉树木材指接工艺研究[J]. 木材加工机械, 2007(1): 10−15. doi: 10.3969/j.issn.1001-036X.2007.01.003 Lin L Y, Fu F. Study on the finger-joint technology for eucalyptus plantation[J]. Wood Processing Machinery, 2007(1): 10−15. doi: 10.3969/j.issn.1001-036X.2007.01.003
[11]	李海栋, 王朝晖, 黄仲华,等. 落叶松结构用胶合木层板指接工艺参数对力学性能的影响[J]. 林产工业, 2014, 41(1): 13−18. doi: 10.3969/j.issn.1001-5299.2014.01.003 Li H D, Wang Z H, Huang Z H, et al. Effects of finger-jointing parameters on mechanical properties of dahurian larch laminate for structural glulam[J]. China Forest Products Industry, 2014, 41(1): 13−18. doi: 10.3969/j.issn.1001-5299.2014.01.003
[12]	Vassileios V. Effect of knife wear on finger-joint strength of silver fir (Abies alba) wood[J]. Wood Material Science & Engineering, 2011, 6(3): 128−131.
[13]	Frederico J N F, Tamara S A F, Daniel S R, et al. Nondestructive evaluation of 2 by 8 and 2 by 10 southern pine dimensional lumber[J]. Forest Products Journal, 2020, 70(1): 1−10.
[14]	张训亚, 殷亚方, 姜笑梅. 两种无损检测法评估人工林杉木抗弯性质[J]. 建筑材料学报, 2010, 13(6): 836−840. doi: 10.3969/j.issn.1007-9629.2010.06.027 Zhang X Y, Yin Y F, Jiang X M. Evaluation of bending properties of Chinese fir plantation by two nondestructive testing methods[J]. Journal of Building Materials, 2010, 13(6): 836−840. doi: 10.3969/j.issn.1007-9629.2010.06.027
[15]	罗彬, 殷亚方, 姜笑梅,等. 3种无损检测方法评估巨尾桉木材抗弯和抗压强度性质[J]. 北京林业大学学报, 2008, 30(6): 137−140. doi: 10.3321/j.issn:1000-1522.2008.06.022 Luo B, Yin Y F, Jiang X M, et al. Evaluating bending and compressive strength properties of Eucalyptus grandia × E. urophylla plantation wood with three nondestructive methods[J]. Journal of Beijing Forestry University, 2008, 30(6): 137−140. doi: 10.3321/j.issn:1000-1522.2008.06.022
[16]	中华人民共和国国家质量监督检验检疫总局. 结构用集成材: GB/T 26899—2011 [S]. 北京: 中国标准出版社, 2011. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. Structural glued laminated timber: GB/T 26899–2011 [S]. Beijing: Standards Press of China, 2011.
[17]	胡绪腾, 辛朋朋, 宋迎东. 基于最弱环理论的缺口件概率疲劳寿命预测方法[J]. 机械科学与技术, 2013, 32(2): 164−169. Hu X P, Xin P P, Song Y D. Probabilistic fatigue life prediction method for notched specimens based on the weakest-link theory[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(2): 164−169.
[18]	国家林业局. 应力波无损测试锯材动态弹性模量方法: LY/T 2382—2014 [S]. 北京: 中国标准出版社, 2015. National Forestry Administration. Standard test method for nondestructive evaluation of lumber using stress wave: LY/T 2382–2014 [S]. Beijing: Standards Press of China, 2015.
[19]	中华人民共和国住房和城乡建设部. 建筑结构可靠性设计统一标准: GB 50068—2018 [S]. 北京: 中国建筑工业出版社, 2019. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Unified standard for reliability design of building structures: GB 50068 –2018 [S]. Beijing: China Architecture & Building Press, 2019.
[20]	龚迎春, 叶琦, 武国芳, 等. 国产落叶松正交胶合木顺纹抗压强度尺寸效应[J]. 木材科学与技术, 2021, 35(1): 42−46. doi: 10.12326/j.2096-9694.2020019 Gong Y C, Ye Q, Wu G F, et al. Effect of size on compressive strength parallel to the grain of cross-laminated timber made with domestic larch[J]. Chinese Journal of Wood Science and Technology, 2021, 35(1): 42−46. doi: 10.12326/j.2096-9694.2020019
[21]	任海青, 郭伟, 费本华, 等. 轻型木结构房屋用杉木规格材机械应力分等研究[J]. 建筑材料学报, 2010, 13(3): 363−366. doi: 10.3969/j.issn.1007-9629.2010.03.018 Ren H Q, Guo W, Fei B H, et al. Mechanical stress grading of Chinese fir dimension lumber for light wood structure houses[J]. Journal of Building Materials, 2010, 13(3): 363−366. doi: 10.3969/j.issn.1007-9629.2010.03.018
[22]	张彦娟. 人工林杉木工程结构集成材工艺及性能研究[D]. 杭州: 浙江林学院, 2008. Zhang Y J. Study on the technology and structural performance of Chinese fir glued-laminated beams[D]. Hangzhou: Zhejiang Forestry University, 2008.
[23]	Yang J L, Evans R. Prediction of MOE of eucalypt wood from microfibril angle and density[J]. European Journal of Wood and Wood Products, 2003, 61: 449−452. doi: 10.1007/s00107-003-0424-3

施引文献(4)

期刊类型引用(3)

1.	毛林海，孔祥涛，梁璞，傅金和，许佳诺. 竹材物理力学性质影响因素研究进展. 世界竹藤通讯. 2024(02): 91-97 . 百度学术
2.	贾舒予，王游，韦鹏练，马欣欣，吴谊民. 竹节结构及力学性能研究现状. 世界竹藤通讯. 2024(03): 90-99 . 百度学术
3.	曹释予，张翔，季加贵，江甜，周雨砚，王雪花. 截面形态对竹条弯曲性能的影响. 家具. 2023(05): 33-37+116 . 百度学术

其他类型引用(1)

资源附件(0)

图(12) / 表(14)

计量

文章访问数: 886
HTML全文浏览量: 293
PDF下载量: 43
被引次数: 4

1. 材料与方法
1.1 材　料
1.2 方　法
1.2.1 实验模态分析
1.2.2 计算模态分析
2. 实验模态分析
2.1 实验设置
2.2 实验模态结果与分析
3. 计算模态分析
3.1 共鸣面板模型的建立
3.2 计算模态分析结果及数据分析
3.3 ANSYS模态分析结果与实验所得结果对比分析
4. 结　　论

1. 材料与方法
1.1 材　料
1.2 方　法
1.2.1 实验模态分析
1.2.2 计算模态分析
2. 实验模态分析
2.1 实验设置
2.2 实验模态结果与分析
3. 计算模态分析
3.1 共鸣面板模型的建立
3.2 计算模态分析结果及数据分析
3.3 ANSYS模态分析结果与实验所得结果对比分析
4. 结　　论

参考文献(23)

施引文献(4)

资源附件(0)

辐射松层板抗弯性能的指接参数优化及无损检测研究

作者简介: 叶琦。主要研究方向：无损检测技术。Email：2434956714@qq.com 地址：100083 北京市海淀区清华东路35号北京林业大学工学院

计量

出版历程