Mixed-mode fracture properties of parallel laminated bamboo lumber
-
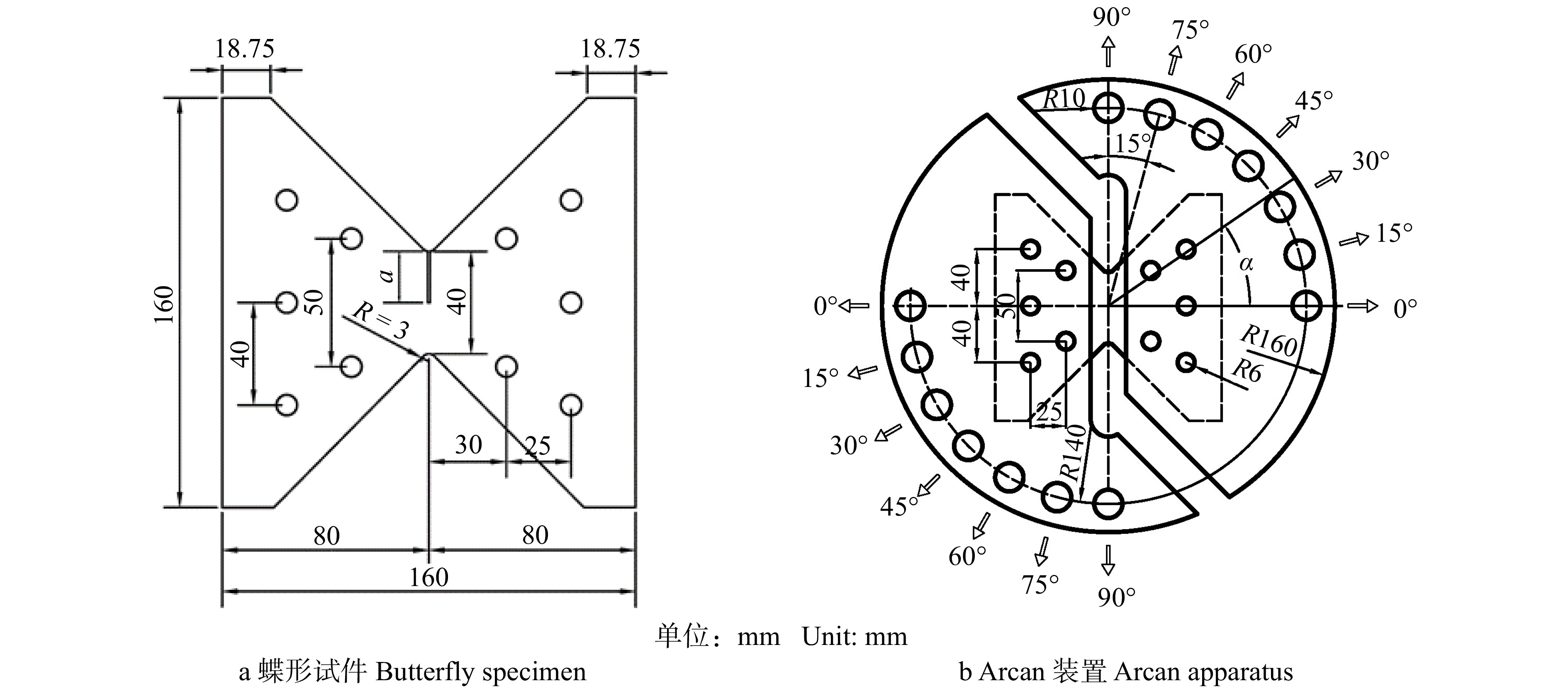
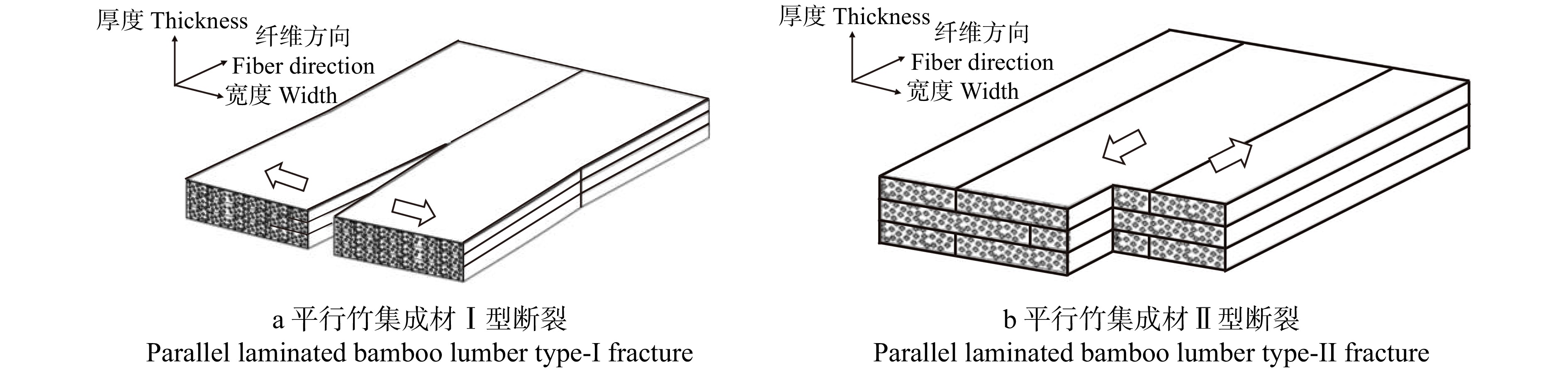
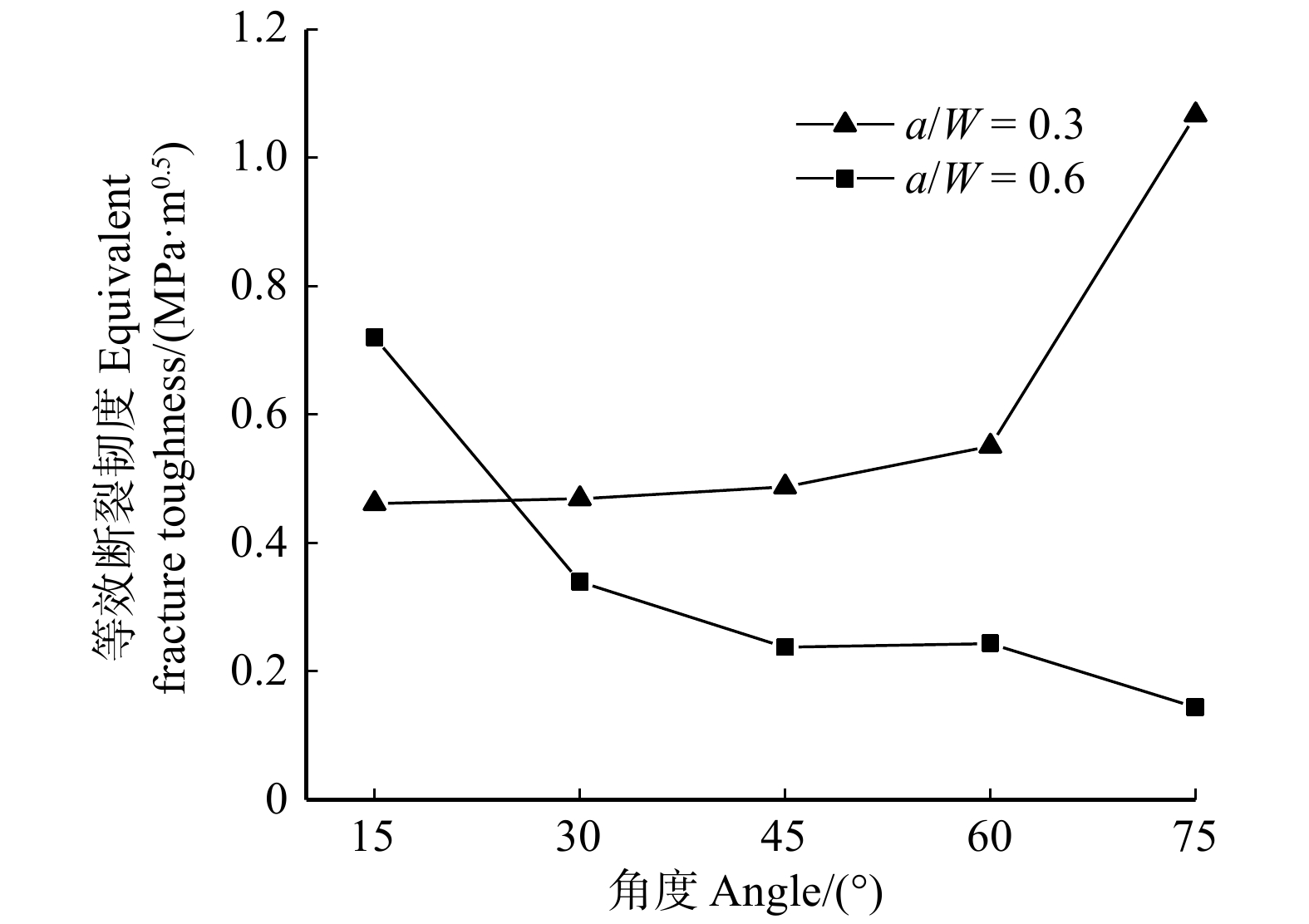
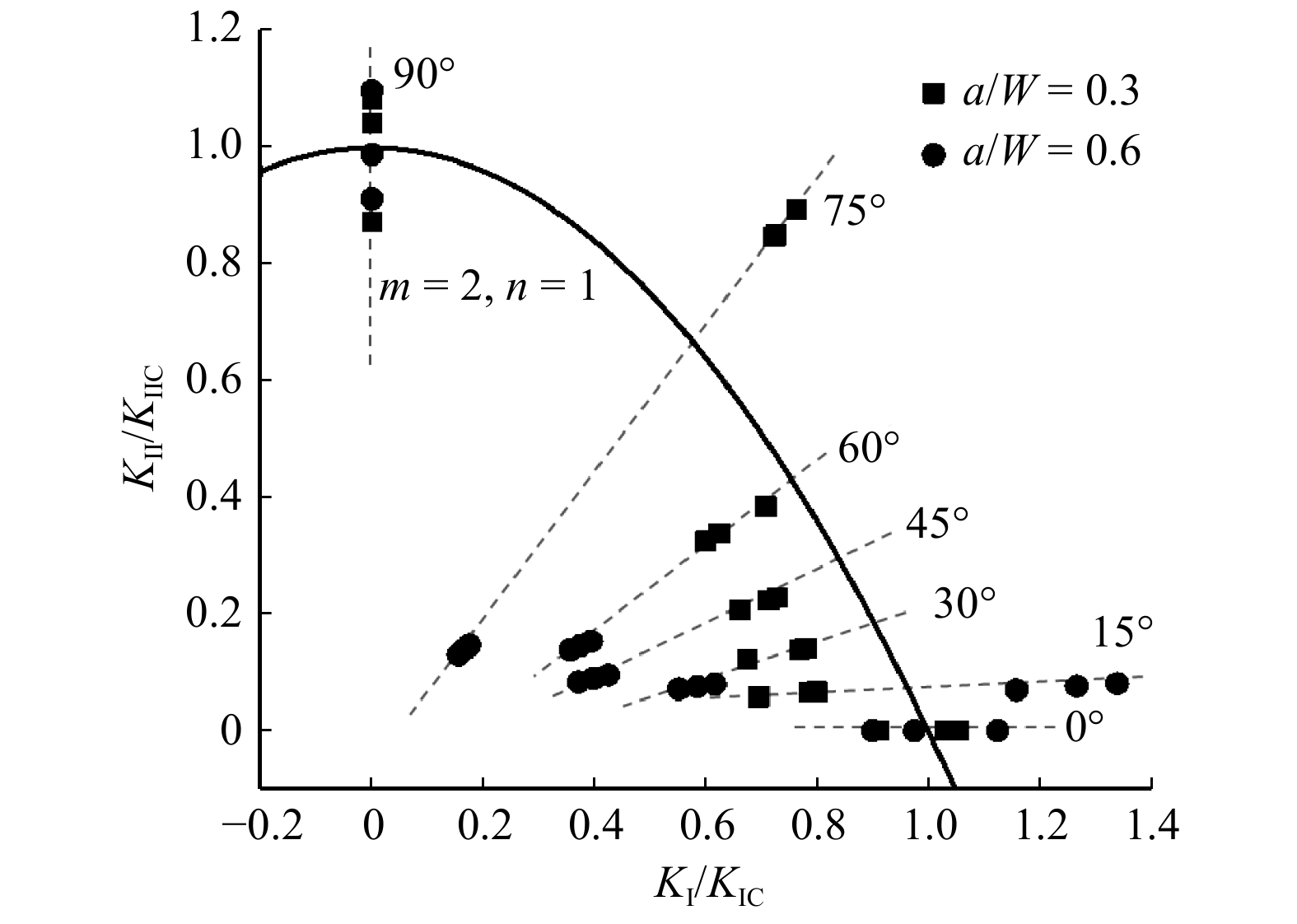
摘要:目的 探究平行竹集成材在复杂应力下沿纤维方向的断裂性能，并根据断裂表面分析其破坏机理，最终得到平行竹集成材复合型断裂基本规律，并建立相应模型。方法 运用Arcan试验测试平行竹集成材蝶形试件沿纤维方向的断裂性能，通过调整加载角度进行不同形式的测试，从而实现试验材料Ⅰ型、Ⅱ型和复合型断裂。设置不同缝高比研究断裂韧带长度对试件断裂韧性的影响；通过测得的极值荷载计算其断裂韧度，并结合断面分析平行竹集成材不同形式断裂的破坏机理；最终通过复合型断裂包络图分析得到平行竹集成材沿纤维方向复合型断裂准则。结果 平行竹集成材沿纤维方向Ⅰ型、Ⅱ型和复合型断裂均为脆性断裂，且试件在复杂应力条件下更容易发生破坏。Ⅰ型断裂试验裂缝主要在薄壁细胞层间和纤维/薄壁细胞组织界面沿纤维方向发展。在Ⅱ型断裂试验中，裂缝在纤维/薄壁细胞组织界面发展的同时，也在薄壁细胞组织多层间开展，形成薄壁细胞组织桥连机制，提高试件承载力。Ⅰ型和Ⅱ型断裂试验中竹纤维均基本不参与断裂。随着试件缝高比改变，Ⅰ型断裂韧度变化幅度较小，Ⅱ型断裂韧度在试件缝高比0.5时有最大值。平行竹集成材复合型断裂试验中，随着加载角度的增加，Ⅰ型断裂韧度分量逐渐减小，Ⅱ型断裂韧度分量逐渐增加；当试件缝高比0.3时，等效断裂韧度随加载角度的增加而增加，缝高比0.6时随加载角度的增加而减小。结论 平行竹集成材试件缝高比为0.3时,复合型断裂准则曲线能够较好描述其复合型断裂特征。Abstract:Objective This paper aims to explore the fracture performance of parallel bamboo glulam along the fiber direction under complex stress, and analyze its failure mechanism according to the fracture surface, finally get the basic law of composite fracture of parallel bamboo glulam, and establish the corresponding model.Method Fracture behavior of parallel butterfly laminated bamboo lumber specimens along the fiber direction was tested with Arcan system. Several fracture modes of parallel laminated bamboo lumber were realized by adjusting loading angle, including type-I, type-II and mixed-mode fracture. The effects of fracture ligament length on fracture toughness of specimens were studied by setting different crack-to-height ratios. The fracture toughness was calculated by the measured extreme load and the failure mechanism of different forms of fracture of parallel laminated bamboo lumber was analyzed by combining the fracture section. Finally, the composite fracture criteria along the fiber direction of parallel laminated bamboo lumber was obtained by the analysis of mixed-mode fracture envelope diagram.Result The fracture of parallel laminated bamboo lumber along the fiber direction of type-I, type-II and mixed-mode fracture was brittle fracture, and the specimens were more likely to be damaged under complex stress. The cracks in type-I fracture test mainly developed along the fiber direction between the parenchyma cell layers and the fiber/parenchyma cell tissue interface. In the type-II fracture test, cracks developed at the fiber/parenchyma cell interface, and at the same time, they also developed among the parenchyma cell layers, forming the bridging mechanism of parenchyma cell tissue and enhancing the bearing capacity of the specimen. In type-I and type-II fracture tests, the fibers were basically not involved in fracture. With the change of crack-to-height ratio, the fluctuation of type-I fracture toughness was small, type-II fracture toughness had the maximum value at 0.5 crack-to-height ratio. With the increase of loading angle in the parallel laminated bamboo lumber mixed-mode fracture test, the type-I fracture toughness component decreased gradually, and the type-II fracture toughness component increased gradually. With the increase of loading angle, the equivalent fracture toughness increased when the crack-to-height ratio of the specimen was 0.3, and decreased when the crack-to-height ratio of the specimen was 0.6.Conclusion When the crack-to-height ratio is 0.3, the fracture criterion curve of the mixed-mode fracture coincides well with fracture characteristics of the parallel laminated bamboo lumber specimens.
-
近年来，以全球变暖为主要标志的气候变化给生态系统带来了巨大的压力[1-4]，陆地生态系统的生产力以及水分利用也受到了严重的影响[5-7]。而树木水分利用效率（water use efficiency，WUE）可以反映生态系统对全球气候变化的响应和描述不同生态系统的碳水循环关系 [8]。因此研究WUE不仅可以揭示生态系统对气候变化响应机理，还可以为区域气候变化对生态系统碳水耦合关系的影响提供科学的评价依据。
因研究目的、对象不同，WUE一般可分为生态系统、群体、叶片、以及个体4个方面。生态系统WUE是指植物消耗单位质量水分所固定的二氧化碳或生产干物质的量，因研究尺度、研究领域及获取数据手段的差异，不同的研究对生态系统WUE的计算往往存在一定的区别[9]。群体水平WUE是植物累计一段时期的干物质积累量与作物耗水量的比值，在植物群体水平上研究WUE时，其测算需要在大田试验中进行，工作复杂繁琐，计算出来的WUE不够准确[10]。叶片尺度上的WUE定义为单位通过蒸腾作用消耗单位水量时光合作用形成的有机物量[11]，在叶片尺度上研究植物的WUE，只能测得叶片尺度瞬时值，缺乏长时间尺度WUE的研究。而基于树木年轮稳定碳同位素的水分利用效率研究可以反映植物个体的长期WUE[12]，已有研究表明这一方法的可行性 [13-15]，并且该方法采样破坏性小，测定简单且不受时间和季节的限制[16]。目前国内外学者也进行了许多关于树木年轮稳定碳同位素方法研究植物WUE对气候变化响应的工作，如路伟伟等[17]研究北京山区油松（Pinus tabuliformis）WUE发现，区域整体WUE年际变化与温度呈显著负相关关系，与降水量呈正相关关系。Kannenberg等[18]研究美国西部灌木丛和森林的WUE发现，随着气候变得越来越干燥，美国西南部植物的WUE快速增加。Gagen等[19]利用树轮δ13C研究北芬诺斯干地亚植物的WUE发现，樟子松（Pinus sylvestris）WUE随着CO2浓度的升高而升高，但随着CO2浓度逐渐升高，樟子松WUE的升高出现了阈值。由于生态系统植被类型的多样性以及水分利用的有效性，气候因子对不同生态系统WUE的影响存在较大的差距，不同生态系统WUE的变化特征以及对气候变化的响应也不同。为此针对不同区域生态系统树木WUE进行研究是非常有必要的。
日本柳杉（Cryptomeria japonica）是庐山植被类型的重要树种组成部分，主要分布在海拔700 m以上的常绿针叶人工林，在水源涵养、净化大气环境、森林游憩等生态功能上发挥了重要的作用[20]，并且有着较高的生态效益和经济效益。因此本文以庐山日本柳杉作为研究对象，基于树木年轮和稳定碳同位素方法，分析气候变化背景下庐山日本柳杉WUE的变化特征以及庐山日本柳杉WUE与主要气候因子之间的关系，有助于庐山日本柳杉的碳汇能力评估以及提升森林的经营管理水平，对评估庐山日本柳杉的碳水耦合关系提供科学的理论支持。
1. 研究方法与数据来源
1.1 研究区概况
庐山位于江西省九江市（115°51′ ~ 116°07′E，29°30′ ~ 29°41′N），东偎鄱阳湖，海拔25.0 ~ 1 473.8 m，是著名的避暑胜地，气温适度，年平均最高温度32 ℃，最低气温−16.8 ℃，全年平均温11.4 ℃，全年平均降雨量1 917 mm，属湿润气候区（图1）。充足的水热条件及海拔的差异，共同造就了庐山丰富的植被资源[21]。高达40种植物在庐山地区首次被发现或者以庐山（牯岭）来命名。在植被类型区域划分上虽然属于亚热带常绿阔叶林，由于海拔高度具有较大的差异，因此植被类型上又极具多样性。海拔在1 000 m以下多为常绿或者是常绿落叶混交林，海拔在1 000 ~ 1 300 m为落叶阔叶林带[22]。生长在海拔较低处的植被由于受到人为活动的影响，植被破坏较为严重，而海拔较高处植被生长相对较好，对生态系统水源涵养的调节具有一定的作用[23]。
1.2 树木年轮的采集与碳同位素的测定
本研究根据国际树木年轮数据库的采样准则[24]，于2019年7月份在庐山3个不同海拔点取样（采样点1、2、3，见图1），海拔分别为800、950和1 150 m，平均树高为18.6、20.0和19.5 m，平均胸径为29.2、30.5和30.1 cm，林分密度为780 株/hm 2，郁闭度 0.6。每个样点取40个样芯。3个采样点的庐山日本柳杉生长良好，受人类活动以及自然灾害影响较小。
通过对日本柳杉样品进行交叉定年[25]，选取其树轮无生长异常、年轮宽度变化趋势较为一致、早晚材年轮界限明显的树芯用于稳定同位素的δ13C测定。具体步骤：用不锈钢刀由外而内逐年剥取全木，某些极窄年份的剥取在显微镜的辅助下进行精确切割，将不同树芯的相同年份合并在一起，置于80 ℃的烘箱中烘干至恒质量，枝剪剪碎之后的木材碎屑用高通量组织研磨仪研磨粉碎，过100目筛后装于5 mL离心管中，用于碳同位素测定分析，然后将样品粉末置于V（苯）∶V（乙醇） = 2∶1混合溶液中抽提24 h，除去树脂、树蜡及单宁类等有机物[26]。天平（精度0.001 mg）称取（0.20 ± 0.05） mg抽提好的样品包裹于锡杯中，在赛默飞稳定同位素质谱仪（delta v advantange）中将样品高温燃烧转换为气体，测量精度0.01‰，试验误差小于0.2‰[27]，测得稳定碳同位素的比值，即13C丰度（δ13C），每测定10个样品插入1个标样来测定仪器的稳定性（处理的树轮样品在江西农业大学森林培育重点实验室内进行分析测定），根据国际标准进行校正后得到日本柳杉稳定碳同位素δ13C值。
1.3 数据来源及处理
本文所用的气象数据来源于中国气象数据网（http://data.cma.cn/site/index.html）的庐山站日气象数据（庐山站的位置见图1），主要包括1968—2018年的平均气温（T）、最高温度、最低温度、相对湿度、降水量（W）、日照时数、平均风速（Ws）等日值数据。
参考1998年联合国粮农组织推荐的计算公式，利用日照时数数据作为输入参数计算庐山多年的太阳辐射（Rs），详细计算步骤可具体参阅文献[28]。为更准确量化庐山干旱严重程度，使用标准化降水蒸散指数（standardized precipitation evapotranspiration index，SPEI）、标准化降水指数（standardized precipitation index，SPI）以及湿度指数（wet index，WI）来表示庐山地区的干旱情况。SPEI和SPI的计算步骤具体参阅文献[29]，WI的计算计算步骤具体参阅文献[30]。利用树木年轮稳定碳同位素值、大气CO2中碳同位素比值和WUE关系来估算庐山日本柳杉1969—2018年的水分利用效率变化，根据Farquhar[13]推荐的公式计算δ13C。
δ13C=(13C/12C)sample−(13C/12C)PDB(13C/12C)PDB×1000‰ (1) 式中：（13C/12C）sample是测试样品13C/12C的摩尔比率； （13C/12C）PDB是标样13C/12C的摩尔比率，δ13C是树木年轮稳定碳同位素比值。
WUE可通过Δ与Ca值之间的关系计算获得[31]。
Δ=δ13Cp−δ13C1+δ13Cp (2) WUE=Ca×(b−Δ)1.6×(b−a) (3) 式中：δ13Cp是大气CO2碳同位素比值，Δ是指树木叶片和空气在光合作用期间同位素水平的差异δ13C的判别值；a是CO2扩散过程中的同位素分馏，取4.4‰，b为CO2羧化过程中的同位素分馏，取27.4‰，此外，系数1.6表示空气中水蒸气与CO2的扩散率之比。Ca为大气二氧化碳浓度，大气二氧化碳浓度由全球系统研究实验室（https://ngdc.noaa.gov/ftp.html）提供。
1.4 统计方法
本文采用一元线性回归模型分析1969—2018年庐山日本柳杉WUE的动态变化趋势[32-33]。并采用曼−肯德尔（M-K）突变分析方法，研究庐山日本柳杉WUE的突变年份[34]。
为预测庐山日本柳杉水分利用效率未来变化趋势，利用Hurst指数（H）进行计算，H是定量描述时间序列的自相似性以及长程依赖性的方法，常采用R/S分析法[35]。本研究中R表示50年日本柳杉WUE序列的极差，S为该时间段WUE的标准差，R/S为极差与标准差的比值，ln为对数函数，τ为偶数序列。当0.5 < H < 1，表明时间序列变化具有持续性的序列，未来的变量与过去的变量是一致的关系；H = 0.5，说明时间序列为相互独立，不存在相互影响的随机序列；0 < H < 0.5，表明时间序列变化具有反持续性的序列，未来的变量与过去的变量是完全相反的序列。其中R2越接近1，显著性越强。植物在生长过程中，气候因子对其生长通常表现出一定的“滞后效应”[36]，树木生长不仅受当年生长季气候因子的影响，还会受到上一年生长季后期气候因子变化的影响。因此，本研究选取上一年7月至当年12月共18个月份的气象数据进行相关性分析和多元回归分析。
2. 结果与分析
2.1 庐山地区各气候因子动态变化
通过对庐山1968—2018年各月气候因子的统计分析得到如图2的结果。从图2可以看出，干旱指数SPEI、WI以及SPI月变化基本一致。大致从2月到6月表现出下降的趋势，呈干旱趋势发展，SPEI和SPI在7月到10月波动较平缓，WI波动较大；干旱指数SPEI、WI以及SPI在12月呈上升趋势（图2a）。月平均气温从1月到7月呈上升趋势，最高气温出现在7月，为22.5 ℃；从8月到12月呈下降趋势，最低气温出现在1月，为0.3 ℃（图2b）。庐山地区的月平均太阳辐射和月平均风速最高出现在7月，为590.37 MJ/m2和4.94 m/s，月平均太阳辐射最低在1月，为285.72 MJ/m2，月平均风速最低在12月，为 3.53 m/s（图2c）。月平均降水量从1月到6月呈上升趋势，降水量最高出现在6月，为299.54 mm，最低出现在12月，为58.33 mm（图2d）。
![]()
图 2 庐山地区1968—2018 年月均SPI、SPEI、WI、T、Rs、Ws和W的变化及趋势Figure 2. Average changes and trends of SPI, SPEI, WI, T, Rs, Ws and W in Lushan Mountain area from 1968 to 20182.2 庐山日本柳杉年轮稳定碳同位素值以及大气二氧化碳同位素值变化规律
如图3a所示，本研究中树轮δ13C序列没有因幼龄效应而表现出明显的趋势变化。日本柳杉δ13C序列变动范围在−23.09‰ ~ −25.67‰，年平均−24.55‰。这与O’Leary等[37]的研究得出自然条件下生长的陆地C3植物碳稳定同位素变化范围在−22‰ ~ −34‰的结论是相符的。庐山日本柳杉的δ13C总体呈递减趋势，平均每10年下降0.34‰。线性回归方程的相关系数R2 = 0.59，δ13C下降趋势显著。但在2001年后有小幅度上升趋势，最大值达到−24.35‰，在2010年呈下降趋势发展，最小值为−25.67‰。庐山δ13Cp序列（1969—2018）变动范围在−7.29‰ ~ −8.93‰（图3b），在1969—2018年总体上是逐年递减的趋势，线性回归方程的相关系数R2 = 0.98，下降趋势显著，平均每10年下降0.32‰。
![]()
图 3 庐山日本柳杉年轮稳定碳同位素值和大气CO2碳同位素值变化及趋势Figure 3. Changes and trends of stable carbon isotope values (δ13C) and atmospheric CO2 carbon isotope values (δ13Cp) of Cryptomeria japonica2.3 庐山日本柳杉水分利用效率的变化特征
如图4a所示，1969—2018年间，庐山日本柳杉的WUE变动范围在91.06 ~ 118.89 μmol/mol，年平均值102.37 μmol/mol，总体呈现上升趋势，平均每10年上升5.2 μmol/mol，2013年出现最大值，为118.89 μmol/mol，最小值出现在1985年，为91.06 μmol/mol。为明确庐山日本柳杉WUE的年际变化特征，本研究对WUE进行了M-K突变分析和Hurst指数分析。从图4b的M-K突变分析可知：WUE呈低−高的趋势走向。1969—1987年，UF呈下降趋势，表明在这一时期，庐山日本柳杉WUE呈下降趋势，1988—2018年，UF呈上升趋势，表明庐山日本柳杉WUE呈上升趋势。庐山日本柳杉WUE的UF、UB交点出现在2004年（图4b），但庐山日本柳杉的WUE交点并不在±1.96临界线值范围内，没有通过0.05的检验，因此该年份的WUE交点上升不具有突变性。在双对数坐标系可以拟合得到年际庐山日本柳杉WUE的时间序列ln（R/S）与ln（τ/2）线性关系图（图4c）。由图4c可知，R/S趋势预测点之间存在良好的线性关系，R2 = 0.91，接近1，模型可行度高，线性拟合效果好。线性拟合的斜率为0.816 8，即Hurst指数估计值为0.816 8，表明庐山日本柳杉的WUE时间序列具有持续性关系，在未来变化中与过去存在较强的相关性，因此未来庐山日本柳杉的WUE呈现上升趋势。
![]()
图 4 庐山日本柳杉水分利用效率的变化特征及趋势WUE. 水分利用效率； UB.逆序时间序列变化；UF.顺序时间序列变化；R.极差；S.标准差；τ.偶数序列；ln.对数函数。WUE, water use efficiency; UB, inverse-order time series variation; UF, sequential time series variation; R, range; S, standard error; τ, even sequences; ln, logarithmic function.Figure 4. Variation characteristics and trends of water use efficiency of Cryptomeria japonica2.4 庐山日本柳杉水分利用效率与气候变化的相关分析以及多元回归模型解释
从庐山日本柳杉WUE序列与月气候变化的相关性分析（图5）可知：庐山日本柳杉WUE与各月气温大多呈正相关关系，与上年的7月、9—11月和当年的2—6月、9—11月呈显著正相关系，其中与上年的9月和当年的3—5月以及9月温度达到极显著正相关系；庐山日本柳杉WUE与各月太阳辐射大多呈负相关，但相关性不显著；WUE与干旱指数上年7—12月份、当年1—12月份干旱指数SPEI、SPI以及WI均呈负相关，但相关性不显著；庐山日本柳杉WUE与上年7—12月、当年1—12月风速均呈极显著负相关关系；WUE与上年7—12月至当年1—12月降水均无显著关系。在庐山日本柳杉的生长过程中， T和Ws在很大程度上驱动了日本柳杉水分利用效率的变化。通过多元线性回归方法将相关气候因子数值进行标准化来描述庐山日本柳杉水分利用效率与月气候因子之间的关系，回归过程选用逐步回归。得到庐山日本柳杉水分利用效率的回归方程。
![]()
图 5 庐山日本柳杉WUE与月气候变化的相关性P 为上年月份，C 为当年月份。**表示在置信度（双侧）为0.01时相关性显著；*表示在置信度（双侧）为0.05时相关性显著。P represents the month in previous year, C represents the month in current year. ** indicates a significant correlation at a confidence level (bilateral) of 0.01, * indicates that the correlation is significant at a confidence level (bilateral) of 0.05.Figure 5. Correlations between WUE of Cryptomeria japonica and monthly climate change in Lushan MountainWUE=58.349−3.733Ws1+1.487T3+1.690T9+1.667T−9−3.377Ws12(P<0.05，R2=0.65) 式中：WUE表示庐山日本柳杉水分利用效率，庐山日本柳杉水分利用效率主要与Ws1（当年1月风速）、T3（当年3月均温）、T9 （当年9月均温）、T−9（上年9月均温）、Ws12（当年12月风速） 相关。
3. 讨 论
3.1 干旱对日本柳杉水分利用效率的影响
水分利用效率是用来衡量植物个体或生态系统水平上碳水耦合关系的重要指标，能够揭示植物个体或生态系统WUE的变化特征[38]。WUE的影响因子随地区和尺度的不同而变化[39]。在本次研究中，本文选3个干旱指数进行庐山日本柳杉水分利用效率对干旱的响应验证发现，无论是SPEI、SPI还是WI，对庐山日本柳杉长期WUE的影响较小或者没有影响，均呈负相关关系（P > 0.05）。Song等[40]对西南亚热带常绿原生林水分利用效率研究表明亚热带常绿森林在干旱年的WUE呈增加趋势。一般认为，不同的生态系统WUE对干旱的响应是不同的。Liu等[41]对中国陆地生态系统水分利用效率与干旱响应研究发现在中国南方，中度和极端干旱会导致WUE下降，严重干旱往往导致WUE略有上升，而在东北和内蒙古中部地区轻微干旱通常会导致WUE增加。杜晓铮等[7]在研究陆地生态系统水分利用效率对气候变化的响应研究综述表明，在不同的气候区域干旱对WUE的影响有所差异，不同生态系统WUE对干旱的响应不同。有研究表明，干旱对植物的水分利用效率存在一定的滞后影响[42]。在本研究中发现，干旱对庐山日本柳杉WUE没有产生滞后影响。在湿润区，干旱发生的同时由于太阳辐射的射入，可能会加快植物的生长速度，同时蒸腾作用也会损失一部分的水分，造成植物WUE呈现出下降的趋势。在本次研究我们也发现，降水与 WUE呈负相关关系（P > 0.05），但相关性不显著。这可能是由于庐山地处湿润区，降水丰富，导致植物叶片气孔导度增大、蒸腾速率增强，造成了庐山日本柳杉水分利用效率的降低。
3.2 气温对日本柳杉水分利用效率的影响
温度对于植物水分利用的影响较为复杂。我们发现，气温对庐山日本柳杉的水分利用效率存在一定的滞后影响，上年的9月气温与庐山日本柳杉WUE呈显著正相关关系，当年的9月气温与庐山日本柳杉WUE也呈显著正相关关系。可能是由于气温适中，植物酶活性增强，从而影响植物水分利用。周佳等[43]利用树木年轮研究河南民权与陕西白水刺槐（Robinia pseudoacacia）水分利用效率对气候的响应表明，两地刺槐WUE与平均温度存在显著正效应关系。一定范围内，温度升高，叶片的气孔导度增加，植物的净光合速率大于蒸腾速率，造成植物WUE升高。崔茜琳等[44]利用MODIS数据研究青藏高原植被水分利用效率，青藏高原植被的WUE 与气温呈显著正相关关系，WUE的敏感性随气温的升高而增加。仇宽彪等[45]对陕西省各植被类型WUE研究时发现，在温度低于11 ℃的地区WUE和温度呈现显著正相关（P < 0.01），而高于11 ℃的地区两者之间没有显著关系（P > 0.05）。在不同的气候区， WUE对温度的响应存在着较大的差异。
3.3 风速对日本柳杉水分利用效率的影响
风会影响植物周围的环境，如降低空气的相对湿度和温度，并通过植物叶片遮挡影响太阳辐射的射入[46]，同时会加速蒸腾速率而相应地降低植物的温度[47]。在不同的生态系统中，水分利用效率对Ws的响应幅度可能不同，甚至可能有完全不同的方向。王云霓[48]在研究宁夏六盘山典型树种水分利用效率中发现华北落叶松（Larix principis-rupprechtii）个体的WUE与Ws是正相关关系（P > 0.05）。在本次研究中发现，庐山日本柳杉WUE与Ws显著负相关关系，特别是当年的1月份和12月份的风速（P < 0.01），对庐山日本柳杉WUE产生了重要的影响。风速越大，植物的蒸腾作用会越强，植物体周围的空气湿度会降低，促使了植物体内的水分更快散失到大气中，造成植物WUE下降。在不同的地区，风速对于植物的WUE影响是有所差异的。庐山自然保护区风速呈现下降的趋势，平均每10年下降0.37 m/s，是日本柳杉WUE年际变化重要的影响因素之一。
3.4 太阳辐射对日本柳杉水分利用效率的影响
太阳辐射是植物光合作用所必须的重要元素之一，对植物WUE的变化也会产生重要影响。如徐晓桃[49]研究黄河源区植被的水分利用效率时发现，黄河源区的植被WUE与Rs是正相关关系。王云霓[48]研究宁夏六盘山典型树种华北落叶松时也发现WUE与Rs呈正相关关系，并且通过了显著性检验（P < 0.01）。一般认为，光照越强，植物的水分利用越高。但庐山日本柳杉WUE在本研究中与Rs未产生显著影响，这与他们的结果不同。一方面可能是由于太阳辐射增加时，植物的光合速率增大，但同时植物的蒸腾也在增大，WUE的变化难以确定。作为碳水循环的综合衡量指标，无论是植物个体的WUE或者是整个生态系统WUE，WUE的变化都是由多个相互作用的物理和生物过程决定，各个气候因子对WUE的变化具有相互协同作用。在评价树木WUE变化对气候因子的响应时，各个气候因子之间综合协同对WUE产生的影响还需进一步探究。
4. 结 论
本研究表明，1969—2018年期间，庐山日本柳杉树轮δ13C值呈下降趋势，WUE变化呈显著升高趋势。温度和风速是影响庐山日本柳杉WUE变化的主要气候因子，WUE与温度具有显著正相关关系，与风速具有显著负相关关系，并且温度对庐山日本柳杉WUE具有一定的滞后影响。而降水、太阳辐射以及干旱指数（SPI、SPEI、WI）对庐山日本柳杉年际WUE的变化未产生显著影响。本研究结果可为在全球气候变化下对庐山日本柳杉生长产生的影响提供理论依据，并且有助于庐山日本柳杉碳汇能力的评估以及提升杉木林的经营管理水平，同时为该地区杉木林生态系统的维护提供理论指导。
-
![]()
图 1 测试试件和试验装置
a代表预制裂缝长度，mm； α为试件加载角度，（°）。a represents the prefabricated crack length, mm; α is the loading angle of specimen, (°).
Figure 1. Test specimen and apparatus
![]()
图 2 平行竹集成材张开型（Ⅰ型）和滑移型（Ⅱ型）断裂
Figure 2. Parallel laminated bamboo lumber open (type-I) and slip (type-II) fractures
![]()
图 3 Ⅰ型断裂试验和荷载−位移曲线
0°代表试件加载角度，0.3、0.5和0.6代表加载试件的缝高比。0° represents the loading angle of the specimen, and 0.3, 0.5 and 0.6 represent the crack-to-height ratios of the loading specimen.
Figure 3. Type-I fracture test and load-displacement curves
![]()
图 5 Ⅱ型断裂试验和荷载−位移曲线
90°代表试件加载角度，0.3、0.5和0.6代表加载试件的缝高比。90° represents the loading angle of the specimen, and 0.3, 0.5 and 0.6 represent the crack-to-height ratio of the loading specimen.
Figure 5. Type-II fracture test and load-displacement curves
![]()
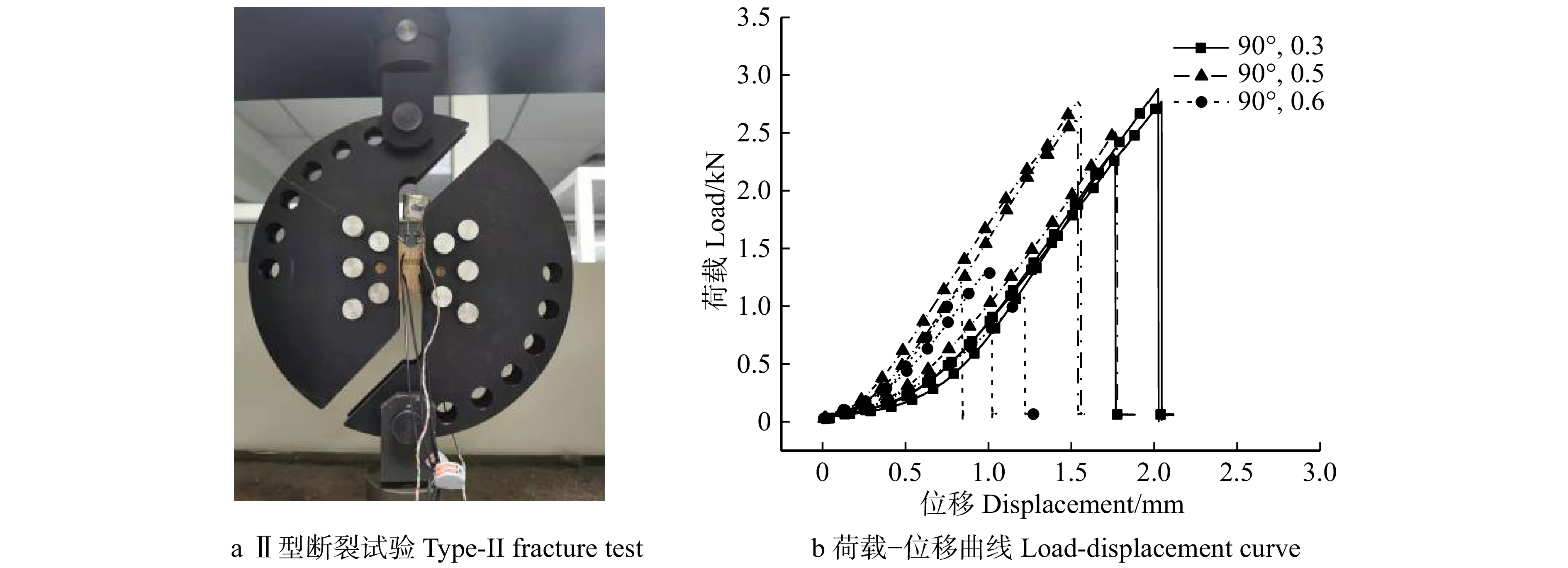
图 7 缝高比0.3和0.6的复合型断裂荷载−位移曲线
15°、30°、45°、60°、75°代表试件加载角度，0.3和0.6代表加载试件的缝高比。15°, 30°, 45°, 60°, 75° represent the loading angle of the specimen, and 0.3 and 0.6 represent the crack-to-height ratio of the loading specimen.
Figure 7. Crack-to-height ratios of 0.3 and 0.6 mixed-mode fracture load-displacement curves
![]()
图 8
缝高比 0.3复合型断裂15° ~ 75°断面 Figure 8.
Crack-to-height ratio of 0.3 mixed-mode fracture 15°−75° failure section ![]()
图 9 缝高比 0.6复合型断裂15° ~ 75°断面
Figure 9.
Crack-to-height ratio of 0.6 mixed-mode fracture 15°−75° failure section ![]()
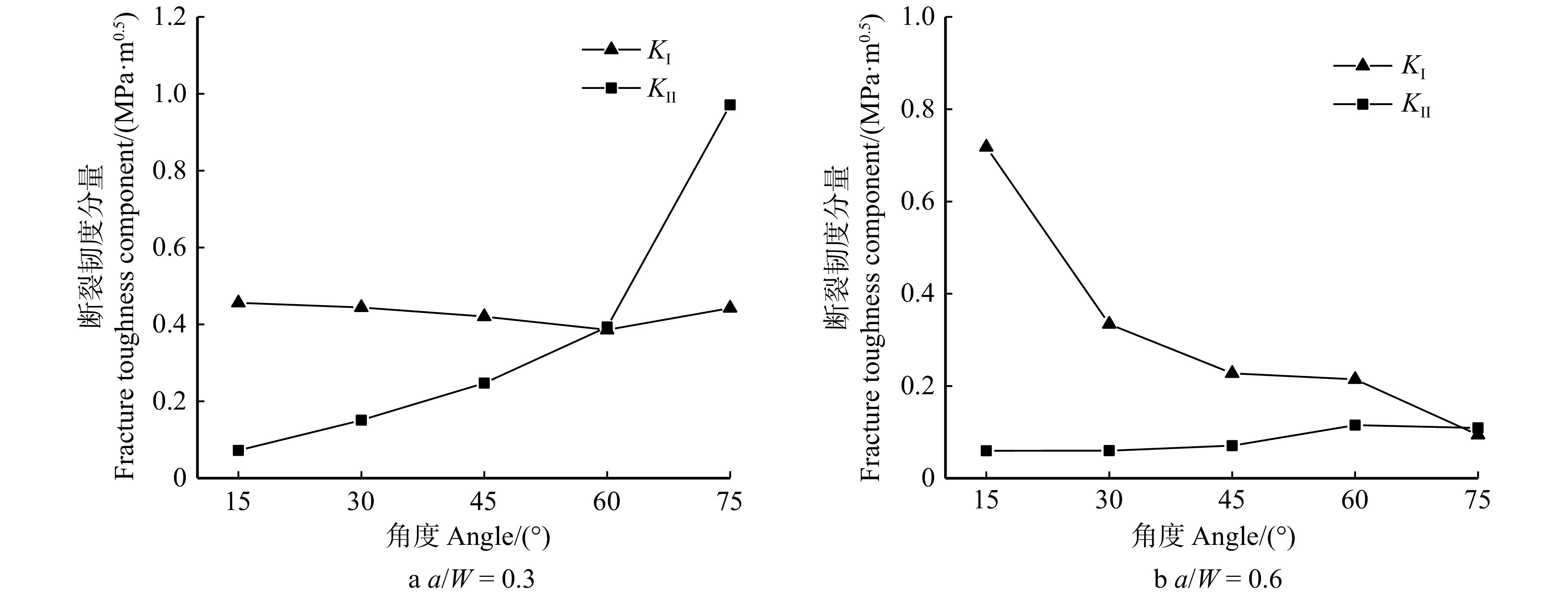
图 10 不同缝高比试件复合型断裂的Ⅰ型和Ⅱ型断裂韧度分量变化趋势
KI和KII为试件Ⅰ型和Ⅱ型断裂韧度分量，MPa·m0.5。KI and KII are the fracture toughness components of specimens type-I and type-II, MPa·m0.5.
Figure 10. Variation trend of type-I and type-II fracture toughness components of composite fractures of specimens with different crack-to-height ratios
![]()
图 11
缝高比0.3和0.6试件的复合型等效断裂韧度 Figure 11. Mixed-mode equivalent fracture toughness of specimens with crack-to-height ratio of 0.3 and 0.6
![]()
图 12 平行竹集成材复合型断裂模型
曲线为当公式（8）中m = 2，n = 1时，所得到的拟合结果；虚线及其上的数据点表示各个试件在0° ~ 90°不同加载条件下的断裂情况。The curve in the figure is the fitting result when m = 2, n = 1 in formula （8）; the dashed line and the data points on it represent the fracture of each specimen under different loading conditions of 0° − 90°.
Figure 12. Composite fracture model of parallel laminated bamboo lumber
表 1 Ⅰ型断裂极值荷载、正应力和断裂韧度
Table 1 Extreme load, normal stress and fracture toughness of type-I fracture
项目 Item 缝高比
Crack-to-height ratio（a/W）0.3 0.5 0.6 极值荷载 Extreme load/kN 0.91 0.44 0.27 正应力 Normal stress/MPa 2.72 1.83 1.39 Ⅰ型断裂韧度
Fracture toughness of type-I fracture (KIC)/(MPa·m0.5)0.66 0.61 0.57 变异系数 Coefficient of variation/% 8.29 2.27 11.46 注：变异系数反映每组3个重复试件的离散程度。下同。Notes: coefficient of variation reflects the dispersion of three repeated specimens in each group. The same below. 
下载: 导出CSV
表 2 Ⅱ型断裂极值荷载、剪应力和断裂韧度
Table 2 Extreme load, shear stress and fracture toughness of type-II fracture
项目 Item a/W 0.3 0.5 0.6 极值荷载 Extreme load/kN 2.66 2.66 1.18 剪应力 Shear stress/MPa 7.91 11.07 6.15 Ⅱ型断裂韧度 Fracture toughness of type-II fracture (KIIC)/(MPa·m0.5) 1.12 1.51 0.79 变异系数 Coefficient of variation/% 29.47 12.58 11.06
下载: 导出CSV
表 3 缝高比0.3试件的极值荷载、正应力和剪应力
Table 3 Extreme load, normal stress and shear stress of specimens with crack-to-height ratio of 0.3
项目 Item 加载角度 Load angle/(°) 15 30 45 60 75 极值荷载 Extreme load/kN 0.66 0.71 0.82 1.07 2.38 正应力 Normal stress/MPa 1.89 1.84 1.74 1.60 1.83 剪应力 Shear stress/MPa 0.51 1.06 1.74 2.77 6.83 变异系数 Coefficient of variation/% 7.51 7.72 5.04 8.81 3.04
下载: 导出CSV
表 4 缝高比0.6试件极值荷载、正应力和剪应力
Table 4 Extreme load, normal stress and shear stress of specimens with crack-to-height ratio of 0.6
项目 Item 加载角度 Load angle/(°) 15 30 45 60 75 极值荷载 Extreme load/kN 0.35 0.18 0.15 0.2 0.17 正应力 Normal stress/MPa 1.74 0.81 0.55 0.52 0.23 剪应力 Shear stress/MPa 0.47 0.47 0.55 0.90 0.86 变异系数 Coefficient of variation/% 7.26 5.56 6.67 5.00 5.88
下载: 导出CSV
-
[1] 李海涛, 宣一伟, 许斌, 等. 竹材在土木工程领域的应用[J]. 林业工程学报, 2020, 5(6): 1−10. Li H T, Xuan Y W, Xu B, et al. Bamboo application in civil engineering field[J]. Journal of Forestry Engineering, 2020, 5(6): 1−10.
[2] 陶慕轩, 聂建国, 樊健生, 等. 中国土木结构工程科技2035发展趋势与路径研究[J]. 中国工程科学, 2017, 19(1): 73−79. Tao M X, Nie J G, Fan J S, et al. Development trends and path for China’s civil and structural engineering science and technology to 2035[J]. Strategic Study of CAE, 2017, 19(1): 73−79.
[3] 李海涛, 张齐生, 吴刚, 等. 竹集成材研究进展[J]. 林业工程学报, 2016, 1(6): 10−16. Li H T, Zhang Q S, Wu G, et al. A review on development of laminated bamboo lumber[J]. Journal of Forestry Engineering, 2016, 1(6): 10−16.
[4] Habibi M K, Lu Y. Crack propagation in bamboo’s hierarchical cellular structure[J]. Scientific Reports, 2014, 4(1): 1−7.
[5] 冼杏娟, 冼定国. 竹材的微观结构及其与力学性能的关系[J]. 竹子研究汇刊, 1990(3): 10−23. Xian X J, Xian D G. The relationship of microstructure and mechanical properties of bamboo[J]. Journal of Bamboo Research, 1990(3): 10−23.
[6] Chen Q, Dai C, Fang C, et al. Mode I interlaminar fracture toughness behavior and mechanisms of bamboo[J]. Materials & Design, 2019, 183: 108132.
[7] Shao Z, Fang C, Tian G. Mode I interlaminar fracture property of moso bamboo (Phyllostachys pubescens)[J]. Wood Science and Technology, 2009, 43(5−6): 527−536. doi: 10.1007/s00226-009-0265-2
[8] Amada S, Untao S. Fracture properties of bamboo[J]. Composites Part B: Engineering, 2001, 32(5): 451−459. doi: 10.1016/S1359-8368(01)00022-1
[9] Reynolds T P S, Sharma B, Serrano E, et al. Fracture of laminated bamboo and the influence of preservative treatments[J]. Composites Part B: Engineering, 2019, 174: 107017. doi: 10.1016/j.compositesb.2019.107017
[10] 李征. 层板胶合木复合型层间断裂特性研究[D]. 大连: 大连理工大学, 2017. Li Z. Study on mixed-mode interlaminar fracture characteristics of glued-laminated timber[D]. Dalian: Dalian University of Technology, 2017.
[11] Ducept F, Davies P, Gamby D. An experimental study to validate tests used to determine mixed mode failure criteria of glass/epoxy composites[J]. Composites Part A: Applied Science and Manufacturing, 1997, 28(8): 719−729. doi: 10.1016/S1359-835X(97)00012-2
[12] Choupani N. Experimental and numerical investigation of the mixed-mode delamination in Arcan laminated specimens[J]. Materials Science and Engineering: A, 2008, 478(1−2): 229−242. doi: 10.1016/j.msea.2007.05.103
[13] Benzeggagh M L, Kenane M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus[J]. Composites Science and Technology, 1996, 56(4): 439−449. doi: 10.1016/0266-3538(96)00005-X
[14] Shameli M, Choupani N. Fracture criterion of woven glass-epoxy composite using a new modified mixed-mode loading fixture[J]. International Journal of Applied Mechanics, 2016, 8(2): 1650015. doi: 10.1142/S1758825116500150
[15] Abu-Okail M, Nafea M, Ghanem M A, et al. Damage mechanism evaluation of polymer matrix composite reinforced with glass fiber via modified Arcan test specimens[J]. Journal of Failure Analysis and Prevention, 2021, 21(2): 451−461. doi: 10.1007/s11668-020-01078-3
[16] Hasanpour R, Choupani N. Rock fracture characterization using the modified Arcan test specimen[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(2): 346−354. doi: 10.1016/j.ijrmms.2008.07.004
[17] Rhême M, Botsis J, Cugnoni J, et al. Mixed mode fracture behavior of welded wood joints investigated with the Arcan test[J]. Wood Science and Technology, 2015, 50(1): 53−69.
[18] Pitti R M, Dubois F, Pop O. A proposed mixed-mode fracture specimen for wood under creep loadings[J]. International Journal of Fracture, 2011, 167(2): 195−209. doi: 10.1007/s10704-010-9544-z
[19] Méité M, Dubois F, Pop O, et al. Mixed mode fracture properties characterization for wood by digital images correlation and finite element method coupling[J]. Engineering Fracture Mechanics, 2013, 105: 86−100. doi: 10.1016/j.engfracmech.2013.01.008
[20] El-Hajjar R F. Experimental study and analytical modeling of translayer fracture in pultruded FRP composites[M]. Atlanta: Georgia Institute of Technology, 2004.
[21] 邵卓平, 吴贻军, 王福利. 竹材横向断裂的物理模型与能量吸收机制: 基本组织开裂与界面脱粘[J]. 林业科学, 2012, 48(7): 108−113. doi: 10.11707/j.1001-7488.20120718 Shao Z P, Wu Y J, Wang F L. The physical model and energy absorbing mechanism of bamboo transverse fracture: the cracking of parenchyma tissue and layering of interface[J]. Scientia Silvae Sinicae, 2012, 48(7): 108−113. doi: 10.11707/j.1001-7488.20120718
[22] 王福利, 王献轲, 周佳硕, 等. 竹材薄壁组织拉伸性能及其变异规律的研究[J]. 北京林业大学学报, 2020, 42(11): 130−137. doi: 10.12171/j.1000-1522.20200203 Wang F L, Wang X K, Zhou J S, et al. Tensile properties and its variation pattern of bamboo parenchyma[J]. Journal of Beijing Forestry University, 2020, 42(11): 130−137. doi: 10.12171/j.1000-1522.20200203
[23] Balcıoğlu H E, Yalçın D. The determination of fracture characterization of knitted fabric reinforced composites using Arcan test[J]. Fibers and Polymers, 2020, 21(4): 849−863. doi: 10.1007/s12221-020-9619-z
[24] Wu E M. Application of fracture mechanics to anisotropic plates[J]. Journal of Applied Mechanics, 1967, 34(4): 967−974. doi: 10.1115/1.3607864
[25] Jurf R A, Pipes R B. Interlaminar fracture of composite materials[J]. Journal of Composite Materials, 1982, 16(5): 386−394. doi: 10.1177/002199838201600503
-
期刊类型引用(3)
1. 陈彩云. 天然染料在鲜茧丝染色中的应用. 轻纺工业与技术. 2023(02): 145-147 . 
百度学术
2. 杨雨桐，张卿硕，符韵林，孙静. 巴里黄檀心材色素的提取及其抑菌活性. 东北林业大学学报. 2020(10): 100-103+119 . 百度学术
3. 王敬贤. 木材染色技术研究进展. 林业科技. 2020(06): 42-47 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 621
- HTML全文浏览量: 167
- PDF下载量: 42
- 被引次数: 7
