Tree height-DBH model for Picea schrenkiana in Tianshan Mountain, Xinjiang of northwestern China based on Bayesian method
-
摘要:目的 贝叶斯统计法能够利用先验信息与样本信息去进行统计推断，可有效提升模型参数的可靠程度和稳定性。方法 本研究以天山云杉林为研究对象，使用3块100 m × 100 m天山云杉调查样地数据，利用经典统计方法（极大似然法）、贝叶斯法构建天山云杉树高−胸径模型。利用随机抽样法抽取80%样地数据进行建模，20%样地数据进行检验，对比分析基于经典方法的非线性模型和非线性混合效应模型以及基于贝叶斯法的贝叶斯模型和层次贝叶斯模型的表现和参数分布。结果 通过对比非线性模型和贝叶斯模型，贝叶斯模型的a、b、c 3个参数置信区间比非线性模型的分别要窄53.86%、46.87%、65.17%。而层次贝叶斯模型和非线性混合效应模型相比，层次贝叶斯模型的固定效应参数置信区间比非线性混合效应模型的要窄37.21%、62.62%、49.31%，但随机效应参数标准差的置信区间更为分散。基于贝叶斯法的模型，其参数标准差均低于基于经典方法的模型。4种树高−胸径模型的拟合结果显示：层次贝叶斯模型的拟合效果优于其他3种模型，其决定系数（R2）为0.961。拟合精度显示：层次贝叶斯模型的预测精度略高于非线性混合效应模型。结论 两种混合模型虽然在拟合结果上没有明显区别，但与非线性混合效应模型相比，层次贝叶斯模型在参数估计的稳定性上更好，其预测更具可靠性。Abstract:Objective Bayesian statistics can use prior information and sample information to make statistical inference, which can effectively improve the reliability and stability of model parameters.Method The data were obtained from three 100 m × 100 m sample plots of Picea schrenkiana, and the classical statistical method (maximum likelihood method) and Bayesian method were used to construct the tree height-DBH model of Picea schrenkiana. 80% of the sample plot data were randomly selected for modelling, and 20% of the sample plot data were validated to compare and analyze the performance and parameter distribution of the non-linear model and non-linear mixed effect model based on the classical method and the Bayesian model and Hierarchical Bayesian model based on the Bayesian method.Result By comparing the non-linear model and Bayesian model, the confidence intervals for the three parameters a, b and c of the Bayesian model were 53.86%, 46.87% and 65.17% narrower than those of the non-linear model, respectively. In contrast, the confidence intervals for the fixed effect parameters of the Hierarchical Bayesian model were 37.21%, 62.62% and 49.31% narrower than those of the non-linear mixed effect model, respectively, but the confidence intervals for the SD of the random effect parameters were more spread out compared with those of the Hierarchical Bayesian model and the non-linear mixed effect model. The models based on the Bayesian approach all had lower parameter SD than those based on the classical approach. The fitting results of the four tree height-DBH models showed that the Hierarchical Bayesian model fitted better than the other three models, with a coefficient of determination (R2) of 0.961. The fitting accuracy showed that the prediction accuracy of the Hierarchical Bayesian model was slightly higher than that of the non-linear mixed effect model.Conclusion Although there is no significant difference between the two mixed models in terms of fitting results, the Hierarchical Bayesian model is better in terms of stability of parameter estimation and its prediction is more reliable compared with the non-linear mixed effect model.
-
磨削是木材加工中必不可少的重要工序，所用磨具大多为砂带，主要用于工件定厚和表面抛光。砂带磨削具有“冷态磨削”和“弹性磨削”的特点，是一种高精度、高效率、低成本的加工技术。材料去除率和表面粗糙度作为最常用的砂带磨削性能指标，是衡量砂带磨削效率、砂带寿命，以及评定加工质量的重要指标。材料去除率是指磨削过程中砂带在单位时间内去除被磨削材料的质量百分比，该指标直接影响到工件的定厚效果和表面粗糙度。影响砂带材料去除率的主要因素有砂带制造工艺、砂带目数、磨削压力、磨削速度和磨削延续长度。任青剑等[1]进行了300M超高强度钢的切入式磨削实验，发现在微观形貌方面，磨粒间距较大的砂带多是因磨粒磨损而失效，这是磨削效率降低的一个原因，但针对磨削效率降低的其他原因及其影响因素的探究仍然不够深入。Torrance[2]建立了磨料磨损模型，并将该方法应用于磨削过程中磨削力和金属材料去除率之间关系的预测以及磨料劣化的预测中。由于木材种类繁多，各项性质差异较大，此模型在木材磨削领域的应用存在局限性，仍需进一步研究探索。表面粗糙度的影响因素主要是关于木材特性的，包括纹理、密度、含水率等。刘博等[3]研究发现磨削表面质量会受到木材材性和加工工艺等因素的影响。Tian等[4]使用磨削效率测试系统和表面粗糙度测量仪进行磨削实验，分析比较了3种试材磨削效率和表面粗糙度的变化规律以及相关因素对磨削效率和表面粗糙度的影响，结果表明：磨削效率与表面粗糙度的变化趋势是随磨削次数的增加而逐渐降低，且同一树种、相同的磨削次数下，横向磨削时的磨削效率高于纵向磨削时的磨削效率。该实验在较为宏观的层面下进行探讨，缺乏对于砂带与试件表面微观形貌的进一步研究与分析。
砂带在磨削材料过程中将不可避免地产生磨损，且砂带的磨损是多个因素共同作用的结果，如磨削压力、砂带速度、工件材料等，在磨削不同材料或不同的磨削条件下的砂带磨损形式也会有差异。Ferguson等[5]在进行磨料磨损实验时，通过改变磨料磨粒尺寸、磨削压力、滑动速度和滑动距离来评估复合材料的磨损率。Malinov等[6]发现随着磨削压力的增加，Fe-B合金的耐磨性降低，磨损机制从微切割变为微切割和微耕的混合模式。在实际生产中，砂带生产厂家无法提供准确的砂带使用寿命，多依赖熟练工人的经验来判别砂带的使用寿命，这在一定程度上影响企业的生产效率和经济效益。随着人工智能和传感技术的发展，木材加工智能化已成为重要的发展方向，智能化控制一方面是提高机械设备的智能化控制程度，更重要的一方面是使切削（包括磨削）过程和结果可控，也就是根据要求达到相应的材料去除效率和表面加工质量[7]。比如美国将砂带磨削应用于汽车制造业的FMS生产线上，从磨削过程和设备控制两方面共同调控以达到最终的生产过程智能化。美国3M公司发明的微晶复制砂带使磨粒形状细致均匀且统一，使得磨削过程变得更加精密和高效[8]。
有关木材磨削方面的研究基础较为薄弱，而金属磨削理论并不完全适用于木材，对于木材砂带磨损和磨削效率方面的研究则是少之又少，砂带磨损机理也尚不明晰，这严重阻碍了木材加工技术和砂带制造技术向高效智能方向的发展。针对以上问题，本研究对水曲柳试件开展砂带磨削实验，分析砂带磨损机理及磨粒磨损对材料去除率和表面粗糙度的影响，进一步完善木材磨削理论，并为发展适用于木材的砂带磨削技术提供理论支持。
1. 材料和方法
1.1 材 料
水曲柳（Fraxinus mandshurica）材质坚韧致密，富弹性，纹理通直，刨面光滑，胶接、油漆性能较好，具有良好的装饰性能，在建筑、飞机、造船、仪器、运动器材、家具等行业应用广泛，因此本研究选用水曲柳作为实验材料，其气干密度为0.76 g/cm3，含水率为5.41%。制备的试件尺寸为46 mm（长） × 46 mm（宽） × 24 mm（厚）；所有试件取自边材，表面平整，无明显缺陷。本研究所选用砂带为60目普通布基疏植砂型砂带（JW342，DEER，韩国）。
1.2 研究方法
1.2.1 砂带磨削实验装置
本研究所使用的实验装置如图1所示。该装置主要由使工作平台作直线往复运动的驱动系统和提供恒定磨削压力的气动装置组成。将砂带展平放置在工作平台上，调节两端的张紧轮，确保砂带张紧固定；将木制试件放置于夹具内，调节夹紧螺母完成试件的装夹；通过立式布置的带直线导轨的气缸（ADNGF-50-40-A，FESTO，德国），为试件提供恒定的磨削压力（约为100 N）；随着试件材料不断去除，其厚度也逐渐减小，试件夹具可沿立式滑轨在气缸导杆行程内下移，使试件与砂带表面始终相接触；驱动系统带动工作平台沿水平滑轨作往复直线运动（平均速度约为0.3 m/s），同时智能计数装置完成磨削次数记录。
![]()
图 1 砂带磨削实验装置示意图1. 气缸Cylinder；2. 机架Framework；3. 砂带Abrasive belt；4. 张紧轮Tensile wheel；5. 水平滑轨Horizontal slideway; 6. 驱动系统Driver system；7. 竖直滑轨Vertical slideway；8. 夹紧装置Fasten device；9. 试件Sample；10. 夹具Fixture.Figure 1. Schematic of abrasive belt sanding apparatus1.2.2 材料去除率表征及表面形貌分析
在本研究中，材料去除率定义为每磨削1 000次后试件的质量变化率。每磨削一次则磨削长度为50 mm，可将磨削次数累计与磨削长度进行换算。实验过程中，采用精密分析天平（BSA4235，Sartorious，德国）对试件和砂带进行称重，且每次称重前使用高压气枪（额定压力为3.0 MPa）去除试件和砂带表面的磨屑，进而计算相应的材料去除率和砂带的质量变化情况，直至材料去除率降至3%以内，认为此时砂带寿命已达极限，砂带上的磨粒已无法完成对试件材料的有效切除。采用3D轮廓仪（VR5000，KEYENCE，日本）对磨削过程中试件磨削表面和砂带表面进行扫描，再通过专业分析软件（VR Series version 3.2.0.277）测定试件磨削表面以及砂带的表面粗糙度，并使用扫描电子显微（日立S-3400N Ⅱ）对试件的磨削表面形貌进行分析。实验中对水曲柳分别进行顺纹磨削（磨削方向平行于木材纹理方向）和横纹磨削（磨削方向垂直于木材纹理方向）。
2. 结果与讨论
2.1 横纹磨削
横纹磨削时，磨粒的切削方向与木材纤维方向基本垂直，磨粒多呈负前角或小后角，锋利的刃口将木材纤维拦腰截断，木材纤维基本上以剥离的形式去除[9-10]。观察发现图2a中有较多细窄且清晰的单个磨粒磨削痕迹，而图2b、2c中这种磨削痕迹则逐渐减少，直至较宽的磨削痕迹占绝大多数。由于现有的磨粒制备技术及植砂工艺，新砂带上的磨粒等高性不好，如图3a所示，切削刃曲率半径很小且参差不齐，所以磨削初期会在试件表面上留下细窄、清晰的磨削痕迹。
![]()
图 2 横纹磨削时水曲柳表面形貌与磨粒磨损示意图Figure 2. Surface topography and grit wear diagram during transverse sanding![]()
图 3 横纹磨削时砂带表面三维形貌图Figure 3. Three-dimensional topography of the belt surface during transverse sanding随着磨削次数增加，高度较高的磨粒由于与试件接触深度加大，会首先发生破碎和脱落，这也就是所谓的“初锐阶段”[11]。从图4b中明显看出，初锐阶段大约在磨削次数5 000次以内，砂带上的磨粒在发生脱落和破碎之外，磨粒的磨损也同时发生，此时砂带质量减小的速率较快，只是砂带脱落、破碎和磨损所占比例不同。图5b中对应的砂带表面粗糙度较高，即磨粒高度之间差异较大，所以更易压入试件进行磨削，故此时对应图4a处材料去除率极高。
![]()
图 4 横纹磨削水曲柳时材料去除率与砂带质量变化Figure 4. Material removal rate of workpiece and the mass variation of abrasive belt during transverse sanding![]()
图 5 横纹磨削时试件、砂带的表面粗糙度Figure 5. Surface roughness of workpiece and abrasive belt during transverse sanding初锐阶段结束后，在图3b中可观察到砂带表面相同高度磨粒的个数明显增加，主要由于试件与磨粒之间的相互作用使得磨粒尖端钝化为小平面，其等高性变好且高度变矮，材料去除率会随之下降。此时磨粒协同干涉作用逐渐显著，从图2b中可以看出在一条较宽的磨削痕迹中有许多条细小的磨削痕迹，但是并没有非常明显且完整的单个磨粒的磨削痕迹，这是由于前一个磨粒所产生的磨削痕迹会被后续的磨粒进行进一步“加工”，而最终体现出来的磨削痕迹是众多磨粒共同作用的效果，消除了之前单个磨粒的磨削痕迹，使磨削痕迹的界限变得模糊，这种多磨粒干涉效应[12]也是使工件表面变光滑的最关键因素。
随着磨削阶段到达中、后期，从图2c中可以看出磨粒将木纤维从两侧挤出翘起，在试件表面犁出凹痕，只能切除少量材料，故材料去除率呈下降趋势并在一定程度上影响了试件表面的粗糙度。从图5可以看出，磨削中期试件表面的粗糙度是比较高的，但磨削后期由于磨粒钝化更加明显且高度更低，如图3c，砂带表面等高性进一步增加，表面的粗糙度迅速降低，磨粒与试件表面接触深度变浅，试件表面发生弹塑性变形，导致几乎无法去除材料，表面凹痕更浅，故可见图5a在中、后期表面粗糙度明显下降。观察图4b可得磨削中期到后期砂带质量基本是线性减小的，也就说明砂带的磨损、脱落、破碎最终达到一个较为平衡的阶段。
2.2 顺纹磨削
顺纹磨削时，切削方向与木材纤维方向基本平行，磨粒是从木材纤维的端向切入木材[13]。与横纹磨削类似，在初期阶段磨粒顶端的曲率半径较小，切削刃较为锋利，如图6a，砂带上磨粒的等高性较差，易压入木材做有效切削，从图7a中可观察到初期阶段试件表面有多条清晰且完整的磨粒磨削痕迹。
![]()
图 6 顺纹磨削时的砂带表面三维形貌图Figure 6. Three-dimensional topography of the belt surface during longitudinal sanding![]()
图 7 顺纹磨削时水曲柳表面形貌和磨削过程示意图Figure 7. Surface topography and the schematic diagram for workpiece during longitudinal sanding process对比图8a与图4a发现，水曲柳横纹磨削时材料去除率整体大于顺纹磨削的材料去除率，且顺纹磨削时材料去除率的下降速率大于横纹的下降速率。这说明砂带在顺纹磨削时更难去除材料，主要由于顺纹磨削过程中，磨粒切入木材时是从木纤维的端头切入，加之磨粒一般为负前角，很难依靠锋利的刃口将木纤维切断，更多的是将其牵扯拉断[14]。从图8b中也可发现此时砂带的磨损速率更快，导致砂带使用寿命也更短。
![]()
图 8 顺纹磨削水曲柳时材料去除率、砂带质量变化Figure 8. Material removal rate of workpiece and the mass variation of abrasive belt during longitudinal sanding随磨削次数增加，砂带磨粒高度降低，顶端刃口曲率半径不断增大，在图7b中可以看到许多较宽的磨削痕迹且在凹痕两侧有较多毛刺及翘起的木纤维，故在图9a中可明显观察到试件表面粗糙度增高。在磨削中期，从图6b可看出，砂带上磨粒脱落，破碎所占比例较大，等高性增大，磨粒与试件的接触深度降低且切割纤维能力减弱，在试件表面发生更多的是耕犁现象，木纤维在多次牵拉下被扯断，如图7b左侧示意图。
![]()
图 9 顺纹磨削时试件、砂带的表面粗糙度Figure 9. Surface roughness of workpiece and abrasive belts during longitudinal sanding至磨削后期，观察图7c发现部分磨削痕迹被木屑填埋，翘起的毛刺被抹平，且凹痕大多较浅，故可见图9a中试件表面粗糙度明显下降。如图6c，此时磨粒整体高度下降，磨粒磨损情况严重，大多仅摩擦试件表面，几乎无法切除材料，同时将折断、翘起的木纤维碾平并填充空隙，使得表面粗糙度降低。但是不难从图9b中发现，顺纹磨削时后期砂带的表面粗糙度更大，这也和切削方式和磨粒破碎形式有关，因为在顺纹切削时纤维大多被拉断，所以磨粒更易受拉力造成破碎和脱落，这也是砂带在顺纹和横纹磨削时的一个主要差异[15]。
2.3 材料去除率、表面粗糙度灰色预测模型
在砂带寿命范围内，累计磨削长度与磨削过程中材料去除率、表面粗糙度间有着密切联系，但由于样本量少[16-17]，且存在如木材非均质、砂带植砂磨粒分布偶然性等较多未知因素，较难建立磨削长度与材料去除率、表面粗糙的回归模型。20世纪80年代邓聚龙教授创立了一种就数找数的方法，即灰色系统生成法。其研究对象是“部分信息已知，部分信息未知”的“小样本”、“贫信息”不确定性系统，用于解决“小样本”、“贫信息”的不确定性问题，这种方法容错率较高，也易于实现模糊控制[18]。因此本研究采用均值GM（1,1）预测模型建立磨削长度与材料去除率、表面粗糙度间的灰色预测模型，如图10所示。
2.3.1 模型预测
在本次模型中，系列特征序列为材料去除率和表面粗糙度，相关因素序列为磨削长度，模型原始数据及建模步骤如下：
第一步，根据表1、2中数据，建立初始材料去除率序列
X(0)1 、表面粗糙度序列X(0)2 。表 1 横纹磨削模型数据Table 1. Model data of transverse sanding序号
No.磨削长度
Sanding length/m表面粗糙度
Surface roughness/μm材料去除率
Material removal rate/%1 200 41.178 15.11 2 400 39.723 13.48 3 600 40.546 15.71 4 800 51.551 7.27 5 1 000 54.409 12.66 6 1 200 63.536 11.39 7 1 400 60.472 8.35 8 1 600 67.846 9.61 注：为提高所建灰色模型的预测精度，选取数据均在砂带最佳使用寿命范围内。下同。Notes: to improve the precision of the established gray model, the selected data is located in the range of optimal abrasive belt life. Same as below. 表 2 顺纹磨削模型数据Table 2. Model data of longitudinal sanding序号
No.磨削长度
Sanding length/m表面粗糙度
Surface roughness /μm材料去除率
Material removal rate/%1 100 42.572 14.57 2 200 78.737 14.96 3 300 69.976 11.70 4 400 79.229 12.13 5 500 71.151 7.43 6 600 79.812 11.40 7 700 81.305 8.46 8 800 81.221 5.77 9 900 74.79 6.53 10 1 000 78.662 4.86 X(0)1=(X(0)1(1),X(0)1(2),X(0)1(3),⋯,X(0)1(n−1),X(0)1(n))X(0)2=(X(0)2(1),X(0)2(2),X(0)2(3),⋯,X(0)2(n−1),X(0)2(n)) 式中：
X(0)1(n) 代表材料去除率第n个数据的原始数值；X(0)2(n) 代表表面粗糙度第n个数据的原始数值；n表示原始数列的个数，本文横纹磨削时n = 8，顺纹磨削时n = 10。第二步，均值GM（1,1）建模。
（1）对原始数据做一次累加得
X(1)1 和X(1)2 ，原始序列的1-AGO生成；（2）
X(1)(n) 表示原始序列第n个数的一阶累加数值，X(0)(n) 表示原始序列第n个数值，构造数据矩阵B和数据向量Y；B=[−12(X(1)(1)+X(1)(2)1−12(X(1)(2)+X(1)(3)1⋮⋮−12(X(1)(n−1)+X(1)(n)1],Y=[X(0)(2)X(0)(3)⋮X(0)(n)] GM（1,1）模型可表示为
Y=Bu ，即[X(0)(2)X(0)(3)⋮X(0)(n)]=[−12(X(1)(1)+X(1)(2)1−12(X(1)(2)+X(1)(3)1⋮⋮−12(X(1)(n−1)+X(1)(n)1][ˆaˆb] （3）计算待估向量
ˆu ；ˆu=(ˆa,ˆb)T=(BT⋅B)−1BTY 式中：a为发展灰数，表示序列的发展趋势；b为内生控制灰数，表示数据间的变化关系。
（4）建立模型。
dX(1)1dt+a1X(1)=b1 dX(1)2dt+a2X(1)=b2 式中：t表示序号1，2，······，n−1，n的连续变量；a1、b1分别为计算材料去除率预估向量的发展灰数和内生控制灰数；a2、b2分别为计算表面粗糙度预估向量的发展灰数和内生控制灰数。
第三步，模型检验。
从图11a中数据计算得到：横纹磨削过程中，材料去除率平均模拟相对误差为18.362%，表面粗糙度的平均模拟相对误差为5.170%。从图11b中数据计算可得：顺纹磨削过程中，材料去除率平均模拟相对误差为13.491%，表面粗糙度的平均模拟相对误差为4.603%。
2.3.2 结果分析
由图11可知：采用灰色模型均值GM（1,1）的预测平均模拟相对误差都是在20%以内。考虑预测系统本身局限性，以及木质材料的各向异性导致原始数据的随机性较高，本身规律性不是很明显的情况下，这些因素都加大了预测难度，一定程度上影响了模拟预测的准确性。故本模型适用于预测水曲柳磨削过程中，磨削长度分别与材料去除率、表面粗糙度之间关系的预测，对实际生产具有借鉴意义。
3. 结 论
木材磨削过程中材料去除行为会影响木材加工表面质量，其影响因素主要有磨削方向、材料种类以及磨削过程中砂带的磨损情况。本文主要研究了水曲柳在不同磨削方向时的材料去除率和试件、砂带表面粗糙度变化情况，探究了磨粒磨损过程及其与材料去除率之间的关系，得出以下结论：
（1）磨削过程中磨削方向对砂带磨损的影响不同，顺纹磨削对砂带上磨粒的磨损大于横纹磨削。磨粒的磨损对材料去除率有较大的影响，磨粒磨损程度越大，材料去除率越小。当材料去除率降低至3%时，可认为达到砂带使用寿命，应及时更换砂带。
（2）磨削过程中，砂带上磨粒的等高性对材料去除率也有较大影响。等高性越差，材料去除率越高。随磨削次数增加，砂带材料去除能力不断下降，试件表面粗糙度则呈现先增大后减小的趋势。
（3）采用灰色模型均值GM（1,1）的预测平均模拟相对误差都是在20%以内。适用于水曲柳磨削过程中磨削长度分别与材料去除率、表面粗糙度之间关系的预测。
-
![]()
图 1 基于建模和检验数据的树高−胸径散点图
Figure 1. Scatter plots of tree height-DBH based on modeling and validating data
![]()
图 2 4种模型的残差分位数
残差的分位数用不同的灰度表示，白色实线代表给定胸径残差的中位数。Quantiles of residuals are shown in different gray scales and solid white lines represent the median of residuals for a given diameter.
Figure 2. Quantiles of residual diagram of the four models
表 1 3个样地基本信息
Table 1 Basic information of three sample plots
样地号
Sample plot No.面积/hm2
Area/ha海拔
Elevation/m坡向
Aspect坡度
Slope/(°)密度/（株·hm−2）
Denstiy/(plant·ha−1)断面积/（m2·hm−2）
Basal area/(m2·ha−1)1 1 1 870 西北 Northwest 21 759 24.55 2 1 1 930 西北 Northwest 20 598 27.03 3 1 1 990 西北 Northwest 19 571 29.70 
下载: 导出CSV
表 2 样地数据基本统计量
Table 2 Basic statistics of sample plot data
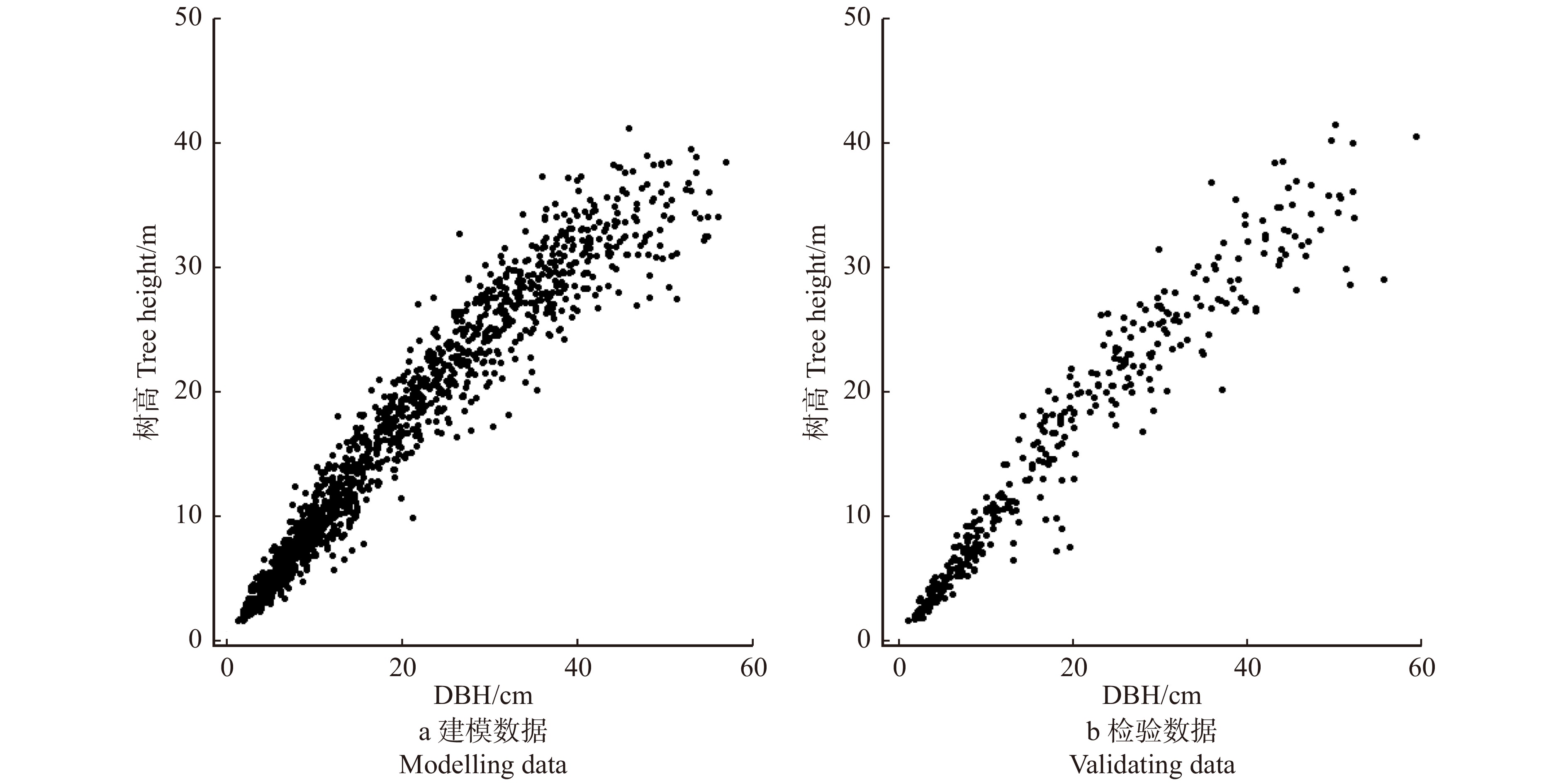
数据
Data样本数
Sample size变量
Variable平均值
Average value最小值
Min. value最大值
Max. value标准差
SD建模数据
Modelling data1 476 树高 Tree height/m 15.76 1.6 41.2 10.206 DBH/cm 18.84 1.4 57.1 13.554 检验数据
Validating data369 树高 Tree height/m 16.03 1.6 41.5 10.502 DBH/cm 19.58 1.1 59.6 14.194
下载: 导出CSV
表 3 备选模型
Table 3 Candidate model
编号 No. 模型 Model 模型表达式 Model expression 1 H=a+bD 2 H−1=a+bD−1 3 lg(H−1.3)=a+blgD 4 lg(H−1.3)=a+bD−1 5 H=a+blgD 6 H=a+bD+cD2 7 H=a+bD−1+cD2 8 幂函数 Power function H=aDb 9 H=1.3+aDb 10 H=1.3+10aDb 11 H=1.3+aDbD−c 12 双曲线 Hyperbola function H=aD/(D+b) 13 H=1.3+aD/(b+D) 14 H=1.3+D2(a+bD)2 15 H=1.3+aDD+1+bD 16 H=1.3+a(D/(1+D))b 17 H=1.3+D2/(a+bD+cD2) 18 H=1.3+a+b/(D+c) 19 Weibull function H=a(1−e−0.05D) 20 H=1.3+a(1−e−bD) 21 H=1.3+a(1+e−bDc) 22 Schumacher function H=1.3+ea+b/(D+1) 23 H=1.3+aeb/D 24 H=1.3+e(a+bDc) 25 Logistic function H=1.3+a/(1+be−cD) 26 H=1.3+a/(1+b−1D−c) 27 Richards function H=1.3+a(1−e−bD)c 28 Gompertz function H=1.3+ae−be−cD 29 H=1.3+aeb/(D+c) 30 H=1.3+ae−bD−c 注：a、b、c为模型参数，H为树高（m），D为胸径（cm）。Notes: a, b, c are model parameters, H is tree height (m), D is DBH (cm).
下载: 导出CSV
表 4 不同参数组合的AIC值
Table 4 AIC values of different parameter combinations
参数组合
Parameter combination赤池信息准则
Akaike information criterion (AIC)a 6 294.80 b 6 308.99 c 6 299.80 a、b 6 278.32 a、c 6 289.68 b、c 6 276.65 a、b、c 6 278.44
下载: 导出CSV
表 5 用于贝叶斯框架下的参数的先验信息
Table 5 Prior information for parameters in the Bayesian framework
模型
Model参数
Parameter先验分布
Prior distribution贝叶斯模型
Bayesian modela a∼N(39.37，0.87132) b b∼N(0.01，0.00042) c c∼N(1.32，0.02062) 层次贝叶斯模型
Hierarchical Bayesian modela a∼N(38.49，0.72722) b b∼N(0.01，0.00032) c c∼N(1.33，0.03882) σb (1/σ2b)∼γ(0.001，0.001) σc (1/σ2c)∼γ(0.001，0.001)
下载: 导出CSV
表 6 备选模型拟合情况
Table 6 Fitting results of candidate models
模型
ModelR2 RMSE 模型
ModelR2 RMSE 模型
ModelR2 RMSE M1 0.930 4 2.716 7 M11 0.947 2 2.596 8 M21 0.947 9 2.351 5 M2 0.945 8 2.396 9 M12 0.945 8 2.396 9 M22 0.936 4 2.598 0 M3 0.936 4 2.596 8 M13 0.941 6 2.488 3 M23 0.931 2 2.701 7 M4 0.931 2 2.701 7 M14 0.908 0 3.124 0 M24 0.947 0 2.370 1 M5 0.876 9 3.613 6 M15 0.931 2 2.701 4 M25 0.938 0 2.564 8 M6 0.947 5 2.358 7 M16 0.933 8 2.649 4 M26 0.947 8 2.352 9 M7 0.886 1 3.476 0 M17 0.947 5 2.359 6 M27 0.947 8 2.351 7 M8 0.940 4 2.513 5 M18 0.203 6 9.194 2 M28 0.945 3 2.408 5 M9 0.936 4 2.596 8 M19 0.880 4 3.561 9 M29 0.947 7 2.354 9 M10 0.936 4 2.596 8 M20 0.942 0 2.479 8 M30 0.947 0 2.370 1
下载: 导出CSV
表 7 4种模型的参数估计
Table 7 Parameter estimation of four models
分类
Classification模型
Model参数
Parameter估计值
Estimate value标准差
SD置信区间
Credible interval2.5% 97.5% 基础模型
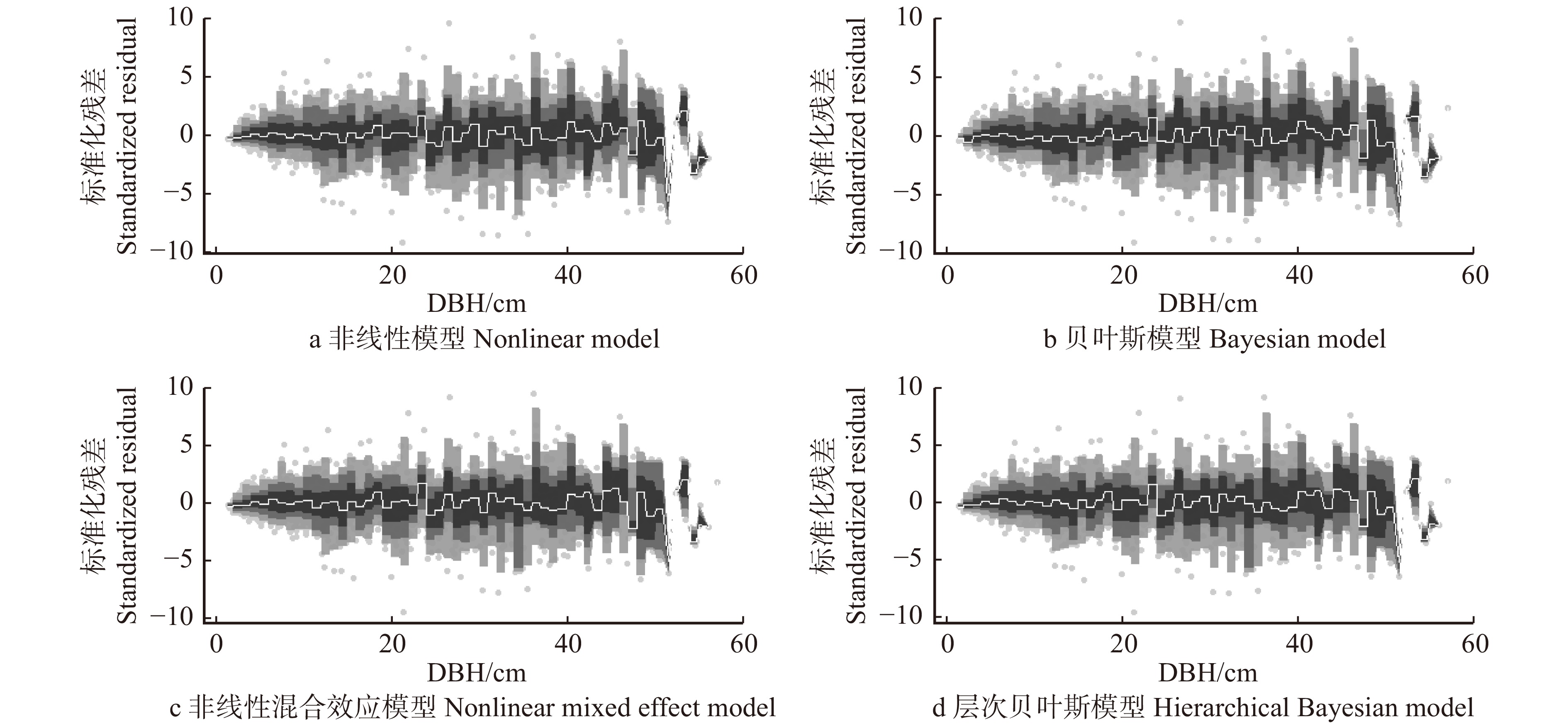
Basic model非线性模型
Nonlinear modela 39.368 0.871 3 37.812 41.237 b 0.011 0.000 4 0.001 0.012 c 1.318 0.020 6 1.278 1.359 贝叶斯模型
Bayesian modela 39.820 0.405 8 38.960 40.540 b 0.011 0.000 3 0.011 0.011 c 1.304 0.008 4 1.290 1.318 混合模型
Mixed model非线性混合效应模型
Nonlinear mixed effect modela 38.488 0.727 2 37.063 39.914 b 0.011 0.001 1 0.009 0.013 c 1.334 0.038 8 1.258 1.410 σb 0.002 0.001 8 0.001 0.004 σc 0.060 0.062 6 0.025 0.142 层次贝叶斯模型
Hierarchical Bayesian modela 38.600 0.451 3 37.770 39.560 b 0.010 0.000 4 0.009 0.011 c 1.316 0.023 6 1.268 1.345 σb 0.001 0.001 7 0.000 0.005 σc 0.057 0.061 9 0.006 0.214
下载: 导出CSV
表 8 4种树高−胸径模型的统计量（n = 1 476）
Table 8 Statistics for the four tree height-DBH models (n = 1 476)
分类
Classification模型
ModelMAE RMSE rRMSE R2 AIC DIC 基础模型
Basic model非线性模型
Nonlinear model1.48 2.06 0.147 0.959 6 324.15 贝叶斯模型
Bayesian model1.51 2.07 0.153 0.959 6 338.10 混合模型
Mixed model非线性混合效应模型
Nonlinear mixed effect model1.47 2.01 0.149 0.961 6 276.65 层次贝叶斯模型
Hierarchical Bayesian model1.47 2.02 0.147 0.961 6 278.64
下载: 导出CSV
表 9 4种树高－胸径曲线模型检验（n = 369）
Table 9 Model test of 4 tree height-DBH curves (n = 369)
分类
Classification模型
ModelMAE RMSE rRMSE 基础模型
Basic model非线性模型
Nonlinear model1.66 2.39 0.154 贝叶斯模型
Bayesian model1.67 2.40 0.159 混合模型
Mixed model非线性混合效应模型
Nonlinear mixed effect model1.64 2.35 0.156 层次贝叶斯模型
Hierarchical Bayesian model1.65 2.39 0.154
下载: 导出CSV
-
[1] 李春明, 李利学. 基于非线性混合模型的栓皮栎树高与胸径关系研究[J]. 北京林业大学学报, 2009, 31(4): 7−12. doi: 10.3321/j.issn:1000-1522.2009.04.002 Li C M, Li L X. Height-diameter relationship for Quercus variabilis Blume plantations based on nonlinear mixed model[J]. Journal of Beijing Forestry University, 2009, 31(4): 7−12. doi: 10.3321/j.issn:1000-1522.2009.04.002
[2] 赵俊卉, 亢新刚, 张慧东, 等. 长白山3个主要针叶树种的标准树高曲线[J]. 林业科学, 2010, 46(10): 191−194. doi: 10.11707/j.1001-7488.20101032 Zhao J H, Kang X G, Zhang H D, et al. Generalized height-diameter models for three main coniferous trees species in Changbai Mountain[J]. Scientia Silvae Sinicae, 2010, 46(10): 191−194. doi: 10.11707/j.1001-7488.20101032
[3] 国家林业和草原局. 中国森林资源报告[M]. 北京: 中国林业出版社, 2019. National Forestry and Grassland Administration. China forest resources report[M]. Beijing: China Forestry Publishing House, 2019.
[4] Dorado F C, Dieguez A U, Anta M B, et al. A generalized height-diameter model including random components for radiata pine plantations in northwestern Spain[J]. Forest Ecology and Management, 2006, 229: 202−213. doi: 10.1016/j.foreco.2006.04.028
[5] 董云飞, 孙玉军, 许昊, 等. 基于非线性混合模型的杉木标准树高曲线[J]. 东北林业大学学报, 2014, 42(11): 72−76, 81. doi: 10.3969/j.issn.1000-5382.2014.11.017 Dong Y F, Sun Y J, Xu H, et al. Generalized height-diameter model for Chinese fir based on nonlinear mixed effects model[J]. Journal of Northeast Forestry University, 2014, 42(11): 72−76, 81. doi: 10.3969/j.issn.1000-5382.2014.11.017
[6] 曾翀, 雷相东, 刘宪钊, 等. 落叶松云冷杉林单木树高曲线的研究[J]. 林业科学研究, 2009, 22(2): 182−189. doi: 10.3321/j.issn:1001-1498.2009.02.006 Zeng C, Lei X D, Liu X Z, et al. Individual tree height-diameter curves of larch-spruce-fir forests[J]. Forest Research, 2009, 22(2): 182−189. doi: 10.3321/j.issn:1001-1498.2009.02.006
[7] 李想, 董利虎, 李凤日. 基于联立方程组的人工樟子松枝下高模型构建[J]. 北京林业大学学报, 2018, 40(6): 9−18. Li X, Dong L H, Li F R. Building height to crown base models for Mongolian pine plantation based on simultaneous equations in Heilongjiang Province of northeastern China[J]. Journal of Beijing Forestry University, 2018, 40(6): 9−18.
[8] Curtis R O. Height-diameter and height-diameter-age equations for second-growth Douglas-fir[J]. Forest Science, 1966(4): 365−375.
[9] Lei X, Peng C, Wang H, et al. Individual height-diameter models for young black spruce (Picea mariana) and jack pine (Pinus banksiana) plantations in New Brunswick, Canada[J]. Forestry Chronicle, 2009, 85(1): 43−56. doi: 10.5558/tfc85043-1
[10] 符利勇. 非线性混合效应模型及其在林业上应用[D]. 北京: 中国林业科学研究院, 2012. Fu L Y. Nonlinear mixed effects model and its application in forestry[D]. Beijing: Chinese Academy of Forestry, 2012.
[11] Li R, Stewart B, Weiskittel A. A Bayesian approach for modelling non-linear longitudinal/hierarchical data with random effects in forestry[J]. Forestry, 2012, 85(1): 17−25. doi: 10.1093/forestry/cpr050
[12] Ellison A M. Bayesian inference in ecology[J]. Ecology Letters, 2004, 7(6): 509−520. doi: 10.1111/j.1461-0248.2004.00603.x
[13] Box G, Tiao G C. Bayesian inference in statistical analysis[M]. Massachusetts: Wiley Press, 1992: 52−65.
[14] Seber G, Wild C J. Nonlinear regression[M]. Massachusetts: Wiley Press, 1989: 164−188.
[15] 王梦皙. 经典方法和贝叶斯方法在单木模型中的应用和比较[D]. 北京: 中国林业科学研究院, 2022. Wang M X. Application and comparison of classical method and Bayesian method in individual tree model[D]. Beijing: Chinese Academy of Forestry, 2022.
[16] Berger J O, Berry D A. Statistical analysis and the illusion of objectivity[J]. Infectious Diseases Newsletter, 1988, 7(8): 159−165.
[17] Jaynes E T. Probability theory: the logic of science[J]. The Mathematical Intelligencer, 2003, 27(2): 33−42.
[18] Mccarthy M A. Bayesian methods for ecology[M]. Cambridge: Cambridge University Press, 2007.
[19] Zhang X, Zhang J, Duan A. A hierarchical Bayesian model to predict self-thinning line for Chinese fir in southern China[J/OL]. PLoS One, 2015, 10(10): e013978[2022−01−01]. doi: 10.1371/journal.pone.0139788.
[20] Zhang X, Duan A, Zhang J, et al. Tree biomass estimation of Chinese fir (Cunninghamia lanceolata) based on Bayesian method[J/OL]. PLoS One, 2013, 8(11): e79868[2022−03−20]. doi: 10.1371/journal.pone.0079868.
[21] 姚丹丹. 基于贝叶斯统计的蒙古栎单木生长模型研究[D]. 北京: 中国林业科学研究院, 2015. Yao D D. Individual tree growth model for Mongolia oak forest with Bayesian statistical inference[D]. Beijing: Chinese Academy of Forestry, 2015.
[22] 姚丹丹, 徐奇刚, 闫晓旺, 等. 基于贝叶斯方法的蒙古栎林单木枯死模型[J]. 北京林业大学学报, 2019, 41(9): 1−8. Yao D D, Xu Q G, Yan X W, et al. Individual-tree mortality model of Mongolian oak forests based on Bayesian method[J]. Journal of Beijing Forestry University, 2019, 41(9): 1−8.
[23] 张雄清, 张建国, 段爱国. 杉木人工林林分断面积生长模型的贝叶斯法估计[J]. 林业科学研究, 2015, 28(4): 538−542. doi: 10.3969/j.issn.1001-1498.2015.04.013 Zhang X Q, Zhang J G, Duan A G. Application of Bayesian method in stand basal area prediction of Chinese fir plantation[J]. Forest Research, 2015, 28(4): 538−542. doi: 10.3969/j.issn.1001-1498.2015.04.013
[24] Bullock B P, Boone E L. Deriving tree diameter distributions using Bayesian model averaging[J]. Forest Ecology and Management, 2007, 242(2): 127−132.
[25] Green, E, Roesch F A, et al. Bayesian estimation for the three-parameter Weibull distribution with tree diameter data[J]. Biometrics, 1994, 50(1): 254−269. doi: 10.2307/2533217
[26] 丁贵杰. 马尾松人工林标准树高曲线模型的研究[J]. 浙江林学院学报, 1997, 14(3): 225−230. Ding G J. Study on standard height curve model of Masson pine planted forests[J]. Journal of Zhejiang A&F University, 1997, 14(3): 225−230.
[27] 郭仲军, 黄继红, 路兴慧, 等. 基于第七次森林资源清查的新疆天然林生态系统服务功能[J]. 生态科学, 2015, 34(4): 118−124. Guo Z J, Huang J H, Lu X H, et al. Nature tree ecosystem services evaluation in Xinjiang based on the Seventh National Forest Assessment data[J]. Ecological Science, 2015, 34(4): 118−124.
[28] 樊伟, 许崇华, 崔珺, 等. 基于混合效应的大别山地区杉木树高−胸径模型比较[J]. 应用生态学报, 2017, 28(9): 2831−2839. Fan W, Xu C H, Cui J, et al. Comparisons of height-diameter models of Chinese fir based on mixed effect in Dabie Mountain area, China[J]. Chinese Journal of Applied Ecology, 2017, 28(9): 2831−2839.
[29] 向玮, 吕勇, 邱林. 湖南黄丰桥林场杉木树高曲线模拟研制[J]. 中南林业调查规划, 2007, 26(1): 16−18. Xiang W, Lü Y, Qiu L. Models for tree height curves of Cunninghamia lanceolata in Huang Fengqiao Forest Farm of Hunan[J]. Central South Forest Inventory and Planning, 2007, 26(1): 16−18.
[30] Joyce H. Bayesian thoughts[J]. Significance, 2004(2): 73−75.
[31] 茆诗松, 王静龙, 濮晓龙. 高等数理统计[M]. 北京: 高等教育出版社, 2006. Mao S S, Wang J L, Pu X L. Advanced mathematical statistics[M]. Beijing: Higher Education Press, 2006.
[32] Gelman A, Carlin J B, Stern H S, et al. Bayesian data analysis[M]. London: Chapman & Hall /CRC Press, 2004.
[33] 张雄清, 张建国, 段爱国. 基于贝叶斯法估计杉木人工林树高生长模型[J]. 林业科学, 2014, 50(3): 69−75. Zhang X Q, Zhang J G, Duan A G. Tree-height growth model for Chinese fir plantation based on Bayesian method[J]. Scientia Silvae Sinicae, 2014, 50(3): 69−75.
[34] 姚丹丹, 徐奇刚, 闫晓旺, 等. 基于贝叶斯方法的蒙古栎林单木树高−胸径模型[J]. 南京林业大学学报(自然科学版), 2020, 44(1): 131−137. Yao D D, Xu Q G, Yan X W, et al. Individual diameter-height model for Mongolian oak forests based on Bayesian method[J]. Journal of Nanjing Forestry University (Natural Sciences Edition), 2020, 44(1): 131−137.
[35] Spiegelhalter D, Thomas A, Best N, et al. WinBUGS user manual version 1.4[M]. Cambridge: MRC Biostatistics Unit, Institute of Public Health, 2007.
[36] Siddhartha C, Edward G. Understanding the metropolis-hastings algorithm[J]. The American Statistician, 1995, 49(4): 327−329.
[37] 薛毅. 统计建模与R软件[M]. 北京: 清华大学出版社, 2007. Xue Y. Statistic modeling with R[M]. Beijing: Tsinghua University Press, 2007.
[38] Zhang X, Duan A, Zhang J, et al. Estimating tree height-diameter models with the Bayesian method[J]. The Scientific World Journal, 2014(2014): 683691.
[39] Zell J, Bösch B, Kändler G. Estimating above-ground biomass of trees: comparing Bayesian calibration with regression technique[J]. European Journal of Forest Research, 2014, 133(4): 649−660. doi: 10.1007/s10342-014-0793-7
[40] 姚丹丹, 雷相东, 张则路. 基于贝叶斯法的长白落叶松林分优势高生长模型研究[J]. 北京林业大学学报, 2015, 37(3): 94−100. Yao D D, Lei X D, Zhang Z L. Bayesian parameter estimation of dominant height growth model for Changbai larch (Larix olgensis Henry) plantations[J]. Journal of Beijing Forestry University, 2015, 37(3): 94−100.
[41] 王冬至, 张冬燕, 李永宁, 等. 基于贝叶斯法的针阔混交林树高与胸径混合效应模型[J]. 林业科学, 2019, 55(11): 85−94. doi: 10.11707/j.1001-7488.20191110 Wang D Z, Zhang D Y, Li Y N, et al. Height-diameter relation for conifer mixed forest based on Bayesian nonlinear mixed-effects model[J]. Scientia Silvae Sinicae, 2019, 55(11): 85−94. doi: 10.11707/j.1001-7488.20191110
-
期刊类型引用(5)
1. 罗斌，杜瑶，柳浩雨，王钦悦，李春瑜，李黎，刘红光. 定组态砂带粒度对刨花板磨削的影响. 北京林业大学学报. 2024(09): 141-150 . 
本站查看
2. 施晨阳，赖文峰，文国卫，蒋天雨，朱晓如，吕增伟，张国防. 基于Maxent模型预测水曲柳的潜在适生区. 西北林学院学报. 2022(02): 149-156 . 百度学术
3. 罗斌，张健，柳浩雨，李黎，刘红光，李昊. 木质材料磨削理论及技术研究进展. 木材科学与技术. 2022(04): 6-12 . 百度学术
4. 杜瑶，田彪，张健，刘红光，罗斌. 中密度纤维板磨削时的砂带磨损研究及寿命评判. 北京林业大学学报. 2021(10): 126-134 . 本站查看
5. 卢冬冬，杨铁牛，杨保健，叶榕伟，阳亚，杜华娜. 肉桂打磨方法优化. 农业工程. 2020(01): 73-78 . 百度学术
其他类型引用(5)
计量
- 文章访问数: 830
- HTML全文浏览量: 157
- PDF下载量: 136
- 被引次数: 10
