Photocatalytic performance of BiVO4-CdS based on wood templates
-
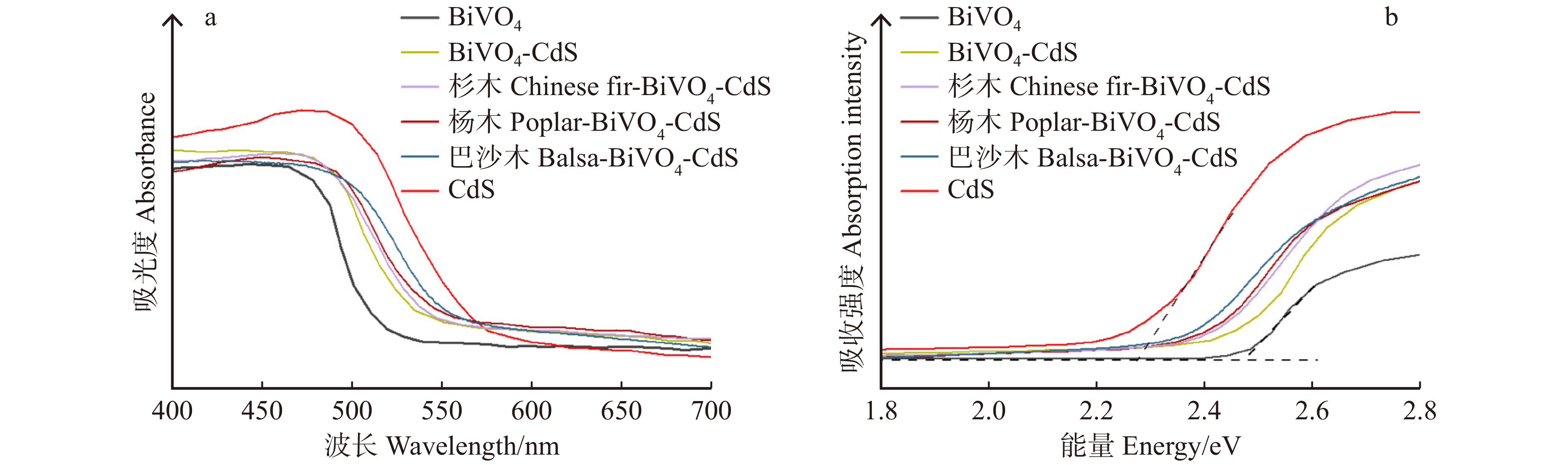
摘要:目的 以木材加工固体废弃物为原料，制备具有木材仿生微纳米孔结构的BiVO4-CdS复合光催化剂，旨在利用木材模板形成更多的异质结结构提高光催化材料的催化性能，拓展其在木材加工染料废水污染处理中的应用。方法 分别采用杉木、杨木、巴沙木3种树种的木材加工固体废料为模板，通过浸渍煅烧和化学沉积两步法制备BiVO4-CdS复合光催化剂，以木材染色废水中的罗丹明B（RhB）为目标降解对象，对复合光催化剂可见光下降解RhB的性能进行评价研究。结果 3种具有木材模板仿生结构的BiVO4-CdS复合光催化剂均表现出良好的吸附−光催化降解RhB的能力。密度较低的巴沙木-BiVO4-CdS在达到吸附平衡后，对RhB有着高达29.26%的去除率；在120 min内可见光下对RhB的降解率为96.01%，其反应速率是无模板BiVO4、BiVO4-CdS的6.69倍和3.37倍。10次吸附−光催化降解循环处理后，材料的降解效率依然达到85%以上。结论 木材模板仿生构造赋予复合光催化剂丰富的孔道结构，低密度树种木材腔壁结构有利于催化剂在浸渍煅烧处理后获得较大的比表面积、稳定的孔结构以及BiVO4-CdS异质结结构形成，进而促进光催化反应过程中污染物分子的快速吸附和降解。Abstract:Objective BiVO4-CdS composite photocatalysts with the wood biomimetic micro-nanopore structure were prepared from wood processing residues. The wood template was used to form more heterojunction structures, improve the catalytic performance of the photocatalytic material and expand the application of BiVO4 in the treatment of wood dye wastewater.Method BiVO4-CdS composite photocatalysts were prepared by impregnation-calcination and chemical deposition using wood processing residues from three species of wood (fir, poplar, and balsa).Result All three BiVO4-CdS composite photocatalysts with wood biomimetic structures exhibited good adsorption-photocatalytic degradation of RhB. The lower-density balsa-wood BiVO4-CdS showed a high removal rate of RhB (29.26%) after reaching adsorption equilibrium; the degradation rate of RhB under visible light was 96.01% in 120 min, and its reaction rate was 6.69 and 3.37 times higher than that of BiVO4 and BiVO4-CdS without a template. After ten adsorption-photocatalytic degradation cycles, the balsa-wood BiVO4-CdS still achieved a degradation efficiency of over 85%.Conclusion The biomimetic structure of wood gives the composite photocatalyst a rich pore structure. The cavity wall structure in the low-density wood facilitates the catalyst to obtain a large specific surface area and stable pore structure after impregnation and calcination treatment. At the same time, it also promotes the formation of the BiVO4-CdS heterojunction structure, which accelerates the rapid adsorption and degradation of pollutant molecules during the photocatalytic reaction.
-
Keywords:
- wood template /
- photocatalytic degradation /
- BiVO4-CdS /
- rhodamine B
-
削度方程是指描述树干直径随着树高的增加而不断变化的方程，用以描述树干形状，故也称为干曲线方程。一般是利用树木胸径、树高、截面高等易测量的林木特征因子作为自变量预测截面直径的多元线性或非线性回归方程[1]。削度方程可以准确预测树干任意高度处的直径，是现代森林清查和林业管理体系的重要工具[2]，被广泛用于估算树干上部直径、计算商品材积和出材率，以及重建树干轮廓等研究中。
国外关于林木干形与削度模型的研究略早于国内，最早的干曲线概念由Kunze提出[3]。之后，削度模型不断发展，根据模型的研究方法，可以分为简单模型、分段模型[4]和可变指数模型。根据是否与材积相容，可分为一致性削度方程和非一致性削度方程。近年来，为了解决单木的自相关，又提出了混合效应模型和多元参数回归模型[5-9]。在不同形式方程的参数估计时，最常用的方法是最小二乘法（OLS）[10]。该方法是基于期望条件下的回归，需要严格的统计学假设条件，数据分布需要满足独立、正态和等方差，而树木生长具有连续性和相关性，难以满足这些要求[11]。另一方面，平均回归估计只能描述因变量的条件均值或中心效应，不能描述非中心条件下的数据结构[12]。
分位数回归是一种利用条件变量来构建模型的方法，可以选取多个分位点对数据结构进行分析，自1978年由Koenker等人提出以来就得到迅速的推广和发展[11]。该方法对研究数据的分布没有严格要求，而且几乎不受异常点的影响，对数据的拟合更为稳健，这对降低由于林木生长异常或数据测量失误等带来的误差具有重要意义。此外，分位数回归不仅可以描述均值条件下自变量与因变量的回归关系，还可以给出响应变量的完整条件分布[13-14]，相较非线性回归更为灵活全面。近年来分位数回归开始应用到林业的研究中，如高慧淋等[15]分别基于分位数回归法、最小二乘法和最大似然法建立了长白落叶松（Larix olgensis）人工林最大密度线模型，发现分位数回归模型的参数估计结果更为稳定；赵梦草等[16]基于分位数回归研究针阔混交林中树高、胸径和活枝高的相关关系，分别构建了一元和二元线性分位数回归模型；张冬燕等[17]基于非线性分位数回归构建了混交林中树高预测模型，发现非线性分位数回归预测模型的精度更高。
杉木（Cunninghamia lanceolata）是我国南方主要的用材树种，具有速生优质的特性，建立精确的削度方程对杉木干形预测和材积计算具有重要意义。目前，已有利用分位数回归模拟樟子松（Pinus sylvestris）和落叶松（Larix spp.）干形的研究[10, 12, 18]，但基于分位数回归估测杉木树干削度尚未见报道。本文以杉木为对象，选取4个具有不同参数个数的可变指数削度方程，基于5折交叉验证，采用分位数回归法构建不同分位点的杉木可变指数削度方程，并与非线性回归结果进行比较分析，为杉木干形的精确预测提供参考。
1. 材料与方法
1.1 数 据
本研究的杉木解析木数据来源于福建省将乐国有林场（117°05′ ~ 117°40′E，26°26′ ~ 27°04′N）。年均温度20 ℃左右，年均降水量约2 700 mm，气候温暖湿润，雨热同期，海拔约400 ~ 800 m，土壤肥沃深厚，主要树种组成有：杉木、马尾松（Pinus massoniana）、毛竹（Phyllostachys edulis
）等。 研究所用的杉木干形数据来自将乐国有林场不同年龄和不同林分的杉木人工林。伐倒样木前，测量树高（H）和胸径（D），按1 m区分段截取圆盘，不足1 m的区分段作为梢头。同时，在树干基部0.01 m和胸径1.3 m处也分别截取圆盘，然后测量每个圆盘东西、南北两个方向的直径，计算平均值作为对应高度处的直径。共计793组干形数据，样木的各调查因子统计情况见表1。
表 1 杉木调查因子统计表Table 1. Basic statistic information of sample trees项目 Item 最小值 Min. 最大值 Max. 平均值 Mean 中位数 Median 标准差 SD 变异系数 CV 树干直径 Stem diameter (di)/cm 0.96 54.00 11.81 11.43 5.987 4.490 树干高 Height along stem (hi)/m 0.0 25.0 8.0 7.0 5.980 3.141 胸径 DBH (D)/cm 4.90 28.40 17.23 17.12 5.003 1.365 树高 Tree height (H)/m 4.1 25.5 17.3 18.2 5.980 1.236 1.2 方 法
1.2.1 基础模型的选择
相较于简单削度方程和分段削度方程，可变指数方程的拟合精度更高[19]，可以较精准地描述不同树干干形和同一林木不同高度的干形变化，是未来的发展方向[20]。根据前人研究选择4个具有不同参数个数、较适宜描述杉木干形的可变指数削度方程作为基础模型[1, 3, 21]，方程的形式如下：
diD=(H−hiH−1.3)(b1+b2)(hiH)14+b3(hiH)12+b4(hiH) (1) di=D(b1+b2log(1−hiH)13)(1−e−b1b2) (2) di=b1Db2(1−hiH)b3(hiH)2+b4hiH+b5 (3) di=b1D(H−hi)b3Hb4 (4) 式中：di为树干直径，hi为树干高，D为胸径，H为树高；b1、b2、b3、b4、b5为参数。
1.2.2 分位数回归
分位数回归相当于将传统回归方法与条件分位数相结合，通过拟合任意分位点的数据，构建多个回归模型，从而描述完全条件分布下自变量与因变量之间的关系。其原理是把损失函数从传统的最小二乘法变成加权的最小二乘法，通过最小化加权离差的绝对值之和来获得方程参数。
QT=1n(∑i:Yi⩾ (5) 式中：QT为损失函数，n为样本数量，T为不同分位点，Yi为不同分位点的估计值，xi为实测值，
{\varepsilon _T} 是分位点为T时的观测值，{\hat f} ({x_i}) 是函数表达式。参数估计使损失函数QT最小，是基于非对称形式的绝对值残差最小化，给不同的Yi值不同的权重，T在0 ~ 1之间内任意取值，模型的参数随着T值的变化而变化。
当取分位点T = t时，权重分别是t和1−t，通过最小化分位数函数QT获得模型的参数，就可以得到该条件下的分位数模型。在不同的分位点下，得到QT函数的参数估计量不同，从而可以得到任意条件下的回归参数。由于分位数回归的损失函数采用加权的绝对离差思想，能有效克服最小二乘回归估计易受异常数据干扰的缺点，得到的回归估计更加稳健。
K折交叉验证是将所有数据分割成K个子样本，不重复的选取其中一个子样本作为测试集，其他K−1个样本用来训练。共重复K次，平均K次的结果作为最终的模型评价指标。使用K折交叉验证可以防止建模样本和检验样本选择不佳而导致模型的精度偏低，而且能够从同样的样本数据中尽可能获得更多的信息。
本文采用的是5折交叉验证。针对每个削度方程，用R 4.0.0的quantile包的nlrq()分别建立分位点为0.1、0.3、0.5、0.7和0.9的5个非线性分位数回归模型，用R4.0.0语言的nls()函数建立非线性回归模型，同时，对传统非线性回归采用自相关函数CAR(2)来消除自相关性。
1.2.3 模型的评价指标
本研究选择的模型评价指标是平均误差（ME）、调整后决定系数（R2）、均方根误差（RMSE）、相对误差（RE）和平均绝对误差（MAE）。具体计算公式：
{\rm{ME}} = \frac{{\displaystyle \sum\limits_{i = 1}^n {\left( {{y_i} - {{{\hat y} }_i}} \right)} }}{n} (6) {\rm{RMSE}} = \sqrt {\frac{{\displaystyle \sum\limits_{i = 1}^n {{{\left( {{y_i} - {{{\hat y} }_i}} \right)}^2}} }}{{ {n - m} }}} (7) {\rm{RE}} = \sum\limits_{i = 1}^n {\left| {\frac{{{y_i} - {{{\hat y} }_i}}}{{{{\bar y}_i}}}} \right|} \times 100 (8) {\rm{MAE}} = \frac{{\displaystyle \sum\limits_{i = 1}^n {\left| {{y_i} - {{{\hat y} }_i}} \right|} }}{n} (9) {R^2} = 1 - \frac{{\displaystyle \sum\limits_{i = 1}^n {{{\left( {{y_i} - {{{\hat y} }_i}} \right)}^2}} }}{{\displaystyle \sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\bar y}_i}} \right)}^2}} }} \times \frac{{n - 1}}{{n - m}} (10) 式中：n为样本数，m为参数个数，yi为不同树高处直径的实测值，
\hat y 为预测值，{{\bar y}_i} 为观测值的均值。2. 结果与分析
2.1 非线性与分位数回归的参数估计
分别采用非线性回归和分位数回归构建杉木的削度方程，每个削度方程选取5个不同的分位点（t = 0.1，0.3，0.5，0.7，0.9）进行拟合，结果见表2。分位数回归选用不同的分位点时，各削度方程的参数均有所变动，会产生不同的估计结果；各削度方程参数的变动程度不同，没有表现出特定的规律；非线性回归参数均在分位数回归参数的变动范围内，说明分位数回归可以主观地选取任意分位值对数据进行拟合，所得到的回归模型会随着分位点的不同而产生不同的拟合结果，其稳健性要优于非线性回归。
2.2 模型拟合结果评价
根据表2所建立的削度方程，计算各方程的调整后决定系数（R2）、平均绝对误差（MAE）、均方根误差（RMSE）、相对误差（RE）和平均误差（ME）5个模型评价指标，比较分位数回归与非线性回归的拟合结果（表3）。可以看出，无论是采用非线性回归还是分位数回归，其R2均在0.90以上，RMSE在1 cm左右，说明这4个削度方程都能较好地描述杉木干形。比较不同分位点的拟合结果可以看出，不同分位点的拟合精度不同；4个削度方程都是分位点为0.5的拟合精度最高；中位数回归与非线性回归的拟合结果相近。其中，模型M1、模型M3和模型M4的拟合精度高于非线性回归，R2分别增加了0.03、0.02和0.04，RMSE分别降低了19.2%、1.36%和8.00%，其余模型评价指标MAE、RE和ME也比非线性回归模型更小。
表 3 基于非线性回归与分位数回归的各削度方程的拟合结果Table 3. Fit-goodness statistics of taper functions based on nonlinear regression and quantile regression模型 Model 建模方法 Modeling method 分位点 Quantile 模型的评价指标 Evaluation index of the model R2 MAE/cm RMSE/cm RE ME/cm M1 非线性回归 Nonlinear regression 0.972 0.635 0.990 3 379.627 0.018 分位数回归 Quantile regression 0.1 0.940 0.953 1.427 5 076.793 0.843 0.3 0.960 0.699 1.122 4 391.152 0.192 0.5 0.975 0.627 0.801 3 337.980 −0.017 0.7 0.970 0.702 1.067 3 738.042 −0.310 0.9 0.930 1.089 1.542 5 799.579 −0.922 0.960 0.830 1.172 4 421.905 0.016 M2 非线性回归 Nonlinear regression 0.971 0.704 1.022 3 749.541 0.017 分位数回归 Quantile regression 0.1 0.920 1.329 1.742 7 076.160 1.263 0.3 0.950 0.932 1.303 4 961.605 0.629 0.5 0.968 0.825 1.180 4 395.446 −0.012 0.7 0.950 0.940 1.320 5 003.610 −0.423 0.9 0.900 1.473 1.877 7 844.500 −1.292 M3 非线性回归 Nonlinear regression 0.972 0.731 1.090 3 892.878 0.032 分位数回归 Quantile regression 0.1 0.940 1.062 1.484 5 656.519 0.999 0.3 0.960 0.764 1.179 4 070.373 0.525 0.5 0.974 0.626 1.008 3 397.303 −0.013 0.7 0.970 0.785 1.102 4 182.318 −0.350 0.9 0.920 0.309 1.685 6 969.442 −1.180 M4 非线性回归 Nonlinear regression 0.975 0.734 1.022 3 949.541 0.170 分位数回归 Quantile regression 0.1 0.940 0.953 1.472 5 076.793 0.843 0.3 0.960 0.726 1.137 3 867.362 0.345 0.5 0.979 0.710 1.003 3 781.487 −0.017 0.7 0.960 0.800 1.165 4 259.591 −0.267 0.9 0.920 1.141 1.664 7 513.007 −1.184 表 2 非线性回归与分位数回归对各削度方程的参数估计结果Table 2. Parameter estimates of taper function based on nonlinear regression and quantile regression模型 Model 建模方法 Modeling method 分位点 Quantile 模型参数 Parameters of model b1 b2 b3 b4 b5 M1 非线性回归 Nonlinear regression 0.783 3 −3.151 0 1.841 7 1.158 8 分位数回归 Quantile regression 0.1 −0.181 2 −0.500 4 0.231 5 1.194 4 0.3 0.623 3 −2.716 6 1.659 8 1.155 7 0.5 0.788 4 −3.388 2 2.068 0 1.191 0 0.7 1.533 0 −5.229 0 3.185 1 1.143 0 0.9 1.947 9 −6.171 4 3.604 2 1.149 8 M2 非线性回归 Nonlinear regression 2.899 0 6.165 0 分位数回归 Quantile regression 0.1 3.024 9 7.133 1 0.3 2.868 6 6.263 2 0.5 2.817 7 5.880 6 0.7 2.769 8 5.519 8 0.9 2.901 9 5.677 5 M3 非线性回归 Nonlinear regression 1.446 6 0.914 6 1.182 4 −1.770 1 1.306 2 分位数回归 Quantile regression 0.1 1.353 6 0.918 7 1.109 7 −1.422 7 1.188 5 0.3 1.312 0 0.929 5 0.766 2 −0.963 6 0.974 8 0.5 1.366 9 0.920 3 0.918 1 −1.223 2 1.029 3 0.7 1.440 5 0.921 0 1.359 8 −1.960 8 1.317 8 0.9 1.516 5 0.925 0 1.179 5 −2.099 3 1.482 4 M4 非线性回归 Nonlinear regression 1.390 6 0.636 9 −0.727 4 分位数回归 Quantile regression 0.1 1.331 0 0.754 1 −0.836 5 0.3 1.294 7 0.677 3 −0.749 8 0.5 1.293 5 0.629 2 −0.700 0 0.7 1.323 9 0.574 5 −0.651 2 0.9 1.598 4 0.565 1 −0.684 9 注：M1、M2、M3和M4分别代表文中的公式(1)、公式(2)、公式(3)和公式(4)。下同。Notes: M1, M2, M3 and M4 represent formula (1), formula (2), formula (3) and formula (4), respectively. The same below. 2.3 不同分位数回归的杉木干形模拟
图1表示不同分位点回归模型对杉木干形的拟合结果，可以看出不同分位点下的树高和对应直径的关系有明显的独立趋势。基于不同分位点的曲线具有不同的形状，可以拟合的数据范围更广泛，无论是均值条件下的数据还是边缘数据，利用分位数回归方法都能进行拟合。分位数回归能更全面地描述杉木干形的变化，包含的信息也更为丰富，选取不同分位点能对整体的干形数据进行拟合，从而分析数据的整体结构。
![]()
图 1 不同分位点模型对杉木干形拟合图Figure 1. Cunninghamia lanceolata stem curve simulation of quantile regression2.4 模型检验
基于5折交叉验证对各削度方程的预测能力进行检验，比较非线性回归模型和中位数回归模型的预测精度，结果见表4。从表4可以看出，基于中位数回归构建的削度方程M1、M2和M3的预测精度高于非线性回归，其MAE分别降低了75.23%、75.12%和16.9%，R2分别增加了0.03、0.05和0.09，其他模型评价指标RMSE、RE和ME也表现优于非线性回归。对于削度方程M4，虽然中位数回归的RMSE比非线性回归略大，但是其MAE、RE和ME分别比非线性回归减少11.44%、2.80%和45.16%。总体来看，中位数回归的预测精度高于非线性回归的预测精度。
表 4 非线性回归模型与中位数回归模型的预测精度检验Table 4. Prediction statistics of nonlinear regression models and median regression models模型
Model非线性回归模型预测精度检验
Prediction statistics of non-linear regression中位数回归模型预测精度检验
Prediction statistics of median regressionR2 MAE/cm RMSE/cm RE ME/cm R2 MAE/cm RMSE/cm RE ME/cm M1 0.972 0.638 0.994 850.911 0.017 0.975 0.158 0.801 797.121 0.007 M2 0.961 0.832 1.180 1109.960 0.088 0.966 0.207 1.155 960.196 0.612 M3 0.970 0.177 1.028 945.102 0.015 0.979 0.174 1.031 926.861 0.011 M4 0.966 0.201 1.095 978.018 0.031 0.966 0.178 1.100 950.730 0.017 为了分析中位数回归与非线性回归对树干不同位置的预测能力，分别计算非线性回归模型和中位数回归模型在不同树干部位的平均绝对误差（MAE），结果见图2。各模型对树干中部（相对高度在0.1 ~ 0.7）的预测精度较高，而对树干基部（相对高度为0 ~ 0.1）和树干上部（相对高度为0.8 ~ 1.0）的预测效果稍差。对树干的绝大部分部位，中位数回归得到的平均绝对误差（MAE）小于非线性回归，且4个削度方程均有此表现，说明中位数回归对杉木干形的预测精度更高。
![]()
图 2 基于非线性回归与中位数回归的各削度方程对不同树高处截面直径的预测结果Figure 2. Prediction results of taper function at different heights of stem based on nonlinear regression and median regression2.5 分位数回归模型应用
为了直观地检验中位数回归法对杉木树干不同部位的预测能力，利用上文建立的削度方程对杉木干形进行预测，结果见图3。可见，基于中位数回归法建立的4个可变指数削度方程对杉木干形均有较好的预测表现，预测值均匀地落在实测值的中部。削度方程M2对树干基部的预测效果偏差，削度方程M1、M3和M4的预测结果相近，但M1的预测值更为集中，说明M1方程更为稳健。
![]()
图 3 中位数回归的杉木干形预测图散点为观测值，线条为中位数回归模型的预测曲线。Points are the observed values and the lines are predicting curves of the median regression models.Figure 3. Stem profile prediction for Chinese fir based on median regression进一步分析不同分位点模型对树干不同部位的预测能力，以削度方程M1为例，计算各分位点模型的平均绝对误差（MAE），结果见图4。随着树干位置的变化，不同分位点模型对直径的预测精度不同，分位点0.7的削度方程对相对树高为0.9的位置处预测精度最高；分位点为0.9时则对相对树高1.0位置处的预测精度最高，其平均绝对误差（MAE）都小于1.0 cm；基于分位点0.3构建的削度方程对树干基部（相对树高为0 ~ 0.1）的预测精度最高，其平均绝对误差（MAE）约为0.75 cm；而基于分位点0.5构建的削度方程对树干绝大部分的预测精度更高。
![]()
图 4 基于不同分位点对树干不同位置的预测结果Figure 4. Prediction results of different stem positions based on varied quantiles3. 讨论与结论
3.1 讨 论
削度方程在编制材种出材率、木材交易方面具有广泛的实用价值，过去对杉木削度方程的研究多基于传统线性或非线性回归[22-25]。为了提高杉木干形的预测精度，同时避免数据的分布不满足非线性回归的假设条件，本研究引入了分位数回归法构建杉木的削度方程。本研究发现，当分位点为0.5时，分位数回归模型的拟合精度和预测精度最高， R2在0.96 ~ 0.97之间，这与辛士冬等[26]的研究结果一致。
基于多个分位点构建的杉木削度模型，既能够描述均值条件下干形数据的分布结构，也能够描述任意分位点树干高度与对应直径的关系。不同的分位条件下，树干高度和对应直径的关系有明显的独立趋势，不同分位点模型对树干不同位置的预测精度有所差别，说明分位数回归模型更具灵活性，付立华等[18]基于分位数回归对华北落叶松（Larix principis-rupprechtii）树干曲线的研究也有类似结论。本文的研究结果表明，分位点为0.9的模型更适宜描述梢头部分干形，分位点为0.3的模型则更适宜描述树干基部干形。由于传统回归对干形基部和梢头的拟合精度往往偏低[4]，分位数回归可以通过构建不同分位点的回归模型，提高对树干不同位置的预测精度。
3.2 结 论
本文构建的分位点为0.1、0.3、0.5、0.7和0.9的模型，每个分位点都具有丰富的信息，能够全面地描述杉木树干削度的变化，预测多个分位水平下杉木树干的直径。整体来看，基于不同分位点构建的4个杉木可变指数削度方程均能收敛，其R2在0.9以上，都能较好地描述杉木干形。对本研究选取的4个可变指数削度方程来说，大部分方程基于中位数回归的拟合精度和预测精度高于非线性回归。基于中位数回归构建的削度方程，其稳健性优于非线性回归，而且不同分位点模型对树干不同位置的预测精度不同，通过构建不同分位点的削度模型，可以提高干形的预测精度。对于研究区的杉木来说，基于削度方程M1建立多分位点回归模型能更准确地估测其干形。
-
![]()
图 1 不同木材模板BiVO4-CdS的XRD图谱（a），不同木材模板BiVO4-CdS的结晶度和晶粒尺寸（b）
Figure 1. XRD patterns of wood-templated BiVO4-CdS (a), the crystallinity and crystalline size of wood-templated BiVO4-CdS (b)
![]()
图 2 复合光催化剂的SEM图像（a ~ e）、巴沙木-BiVO4-CdS的TEM图像（i）和EDS图像（f ~ h，j ~ l）
Figure 2. SEM images of the composite catalysts (a−e); TEM image (i) and EDS mapping (f−h, j−l) of balsa-BiVO4-CdS
![]()
图 4 BiVO4-CdS的吸附−脱附曲线（a）以及孔径分布曲线（b）
Figure 4. N2 adsorption-desorption curves of BiVO4-CdS (a) and pore size distribution (b)
![]()
图 5 BiVO4-CdS的DRS图谱（a）和禁带宽度图谱（b）
Figure 5. DRS spectra of BiVO4-CdS (a) and band-gap diagram (b)
![]()
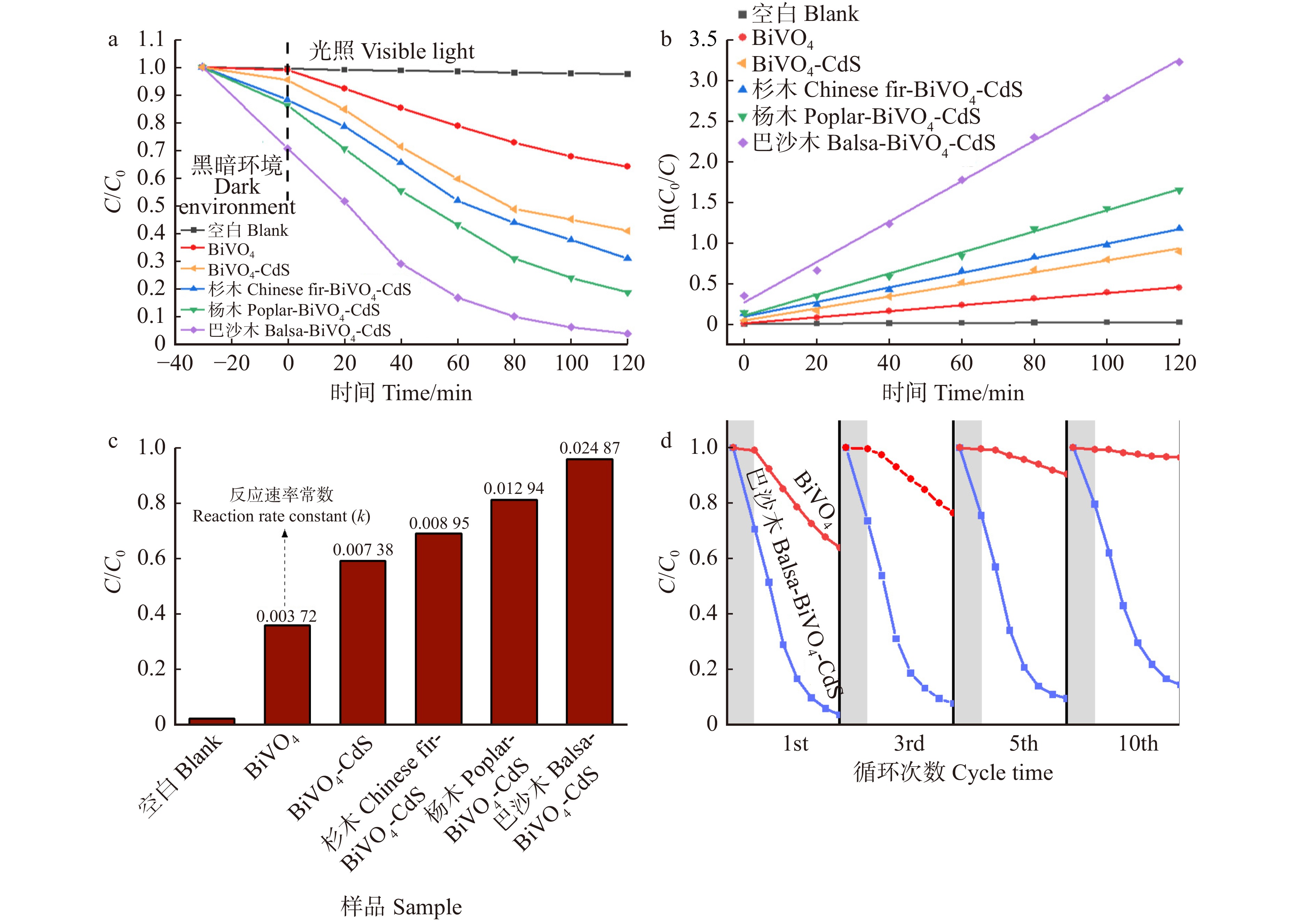
图 6 BiVO4-CdS对RhB的光催化降解曲线（a）、RhB降解的一级动力学拟合曲线（b）、反应速率常数与降解率的关系图（c），RhB的光催化降解循环（d）
C为取样时RhB的质量浓度，mg/L；C0为RhB的初始质量浓度，mg/L。C is the concentration of RhB at the time of sampling, mg/L. C0 is the initial concentration of RhB, mg/L.
Figure 6. Photocatalytic degradation curves (a), first-order kinetic fitting curves (b), reaction rate constant and degradation rate (c), and degradation cycle curves (d)
![]()
图 7 巴沙木-BiVO4-CdS循环降解后的XRD图谱（a）和SEM图像（b）
Figure 7. XRD pattern (a) and SEM image (b) of balsa-BiVO4-CdS after cyclic degradation
![]()
图 8 羟基自由基EPR图谱（a）、超氧阴离子EPR图谱（b）和光催化机理（c）
Figure 8. EPR spectra of ·OH (a) and ·O2− (b), photocatalytic mechanism (c)
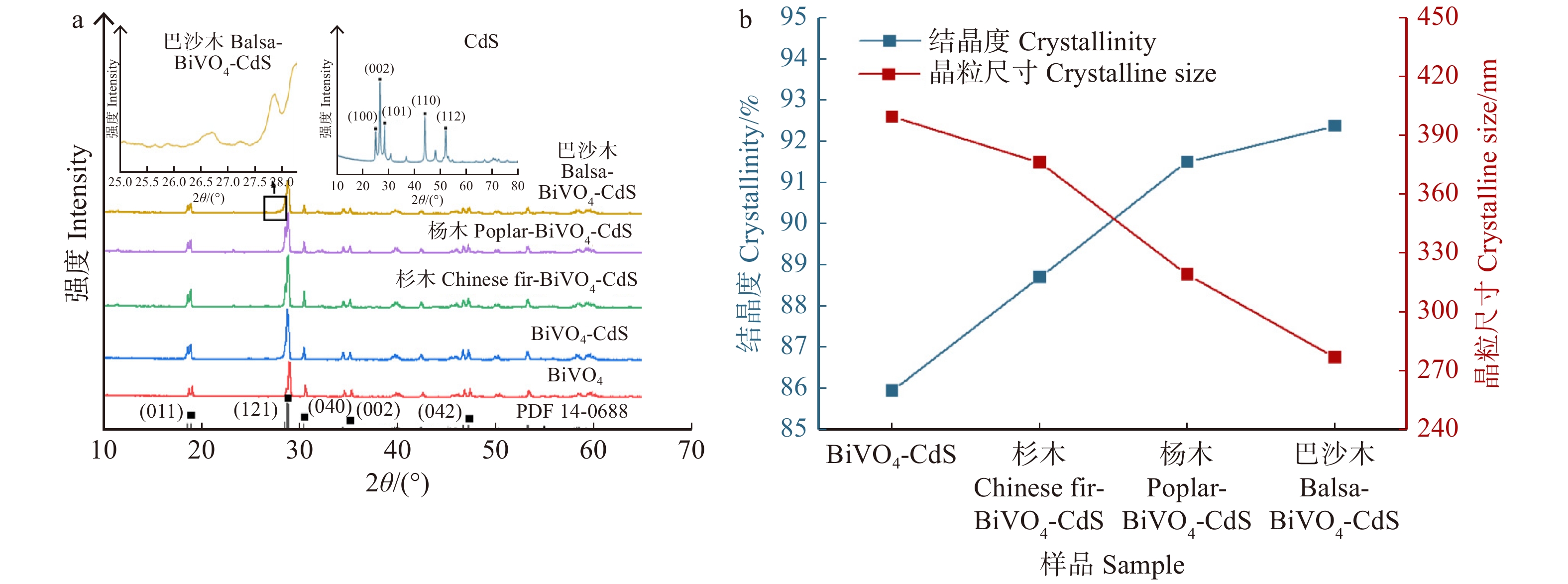
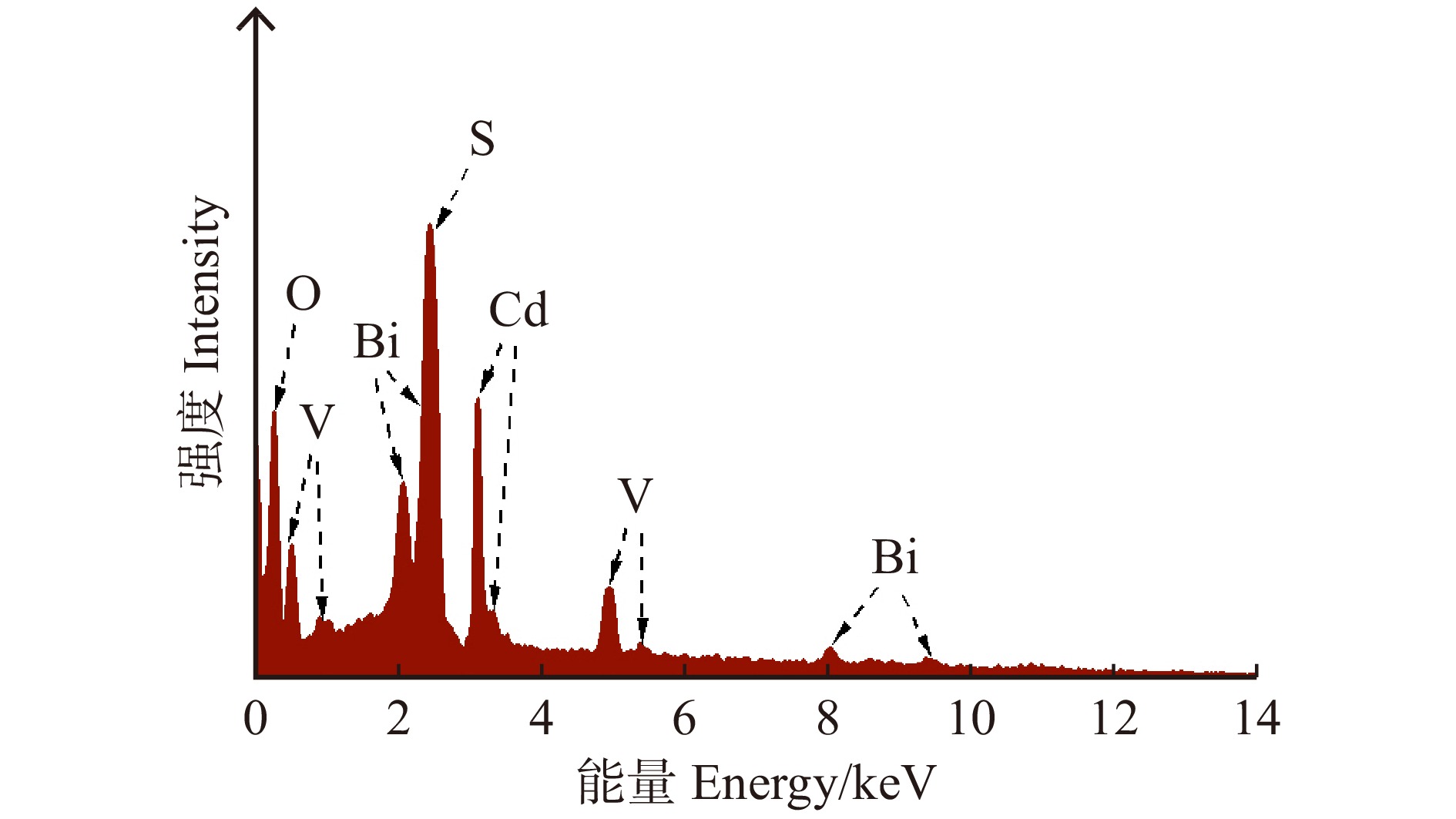
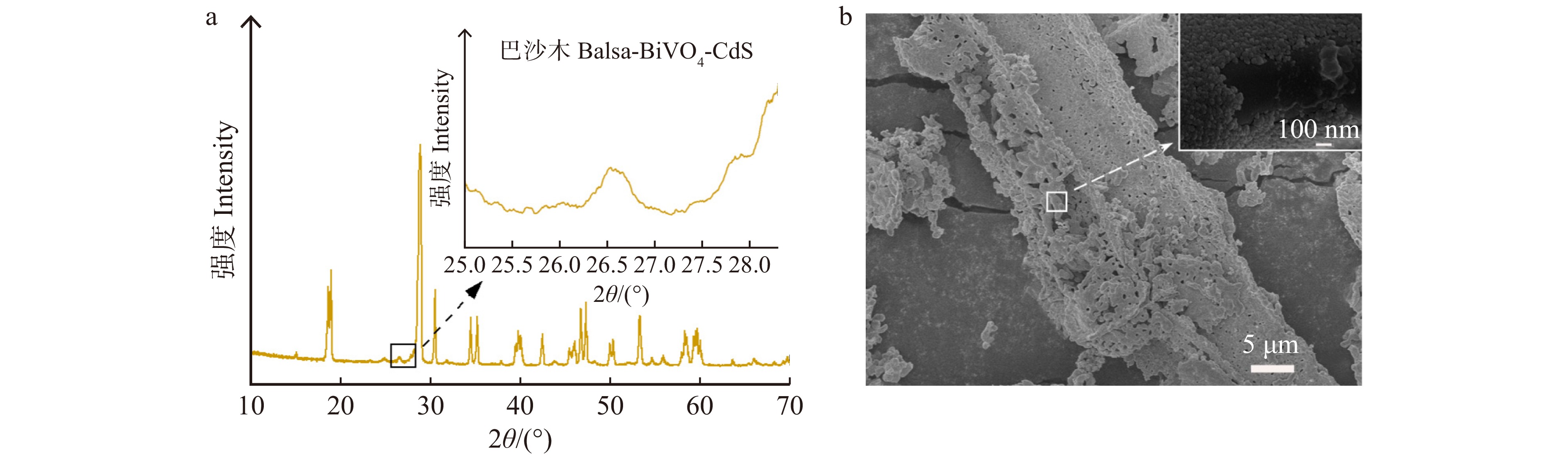
表 1 巴沙木-BiVO4-CdS中各元素的质量和原子百分数
Table 1 Mass percent and atomic percent of each element in the balsa-BiVO4-CdS
元素
Element质量百分数
Mass percent/%原子百分数
Atomic percent/%Bi 36.27 9.89 V 8.37 10.24 O 10.12 39.17 Cd 34.56 21.02 S 10.68 19.68 
下载: 导出CSV
表 2 木材模板BiVO4-CdS的孔结构参数
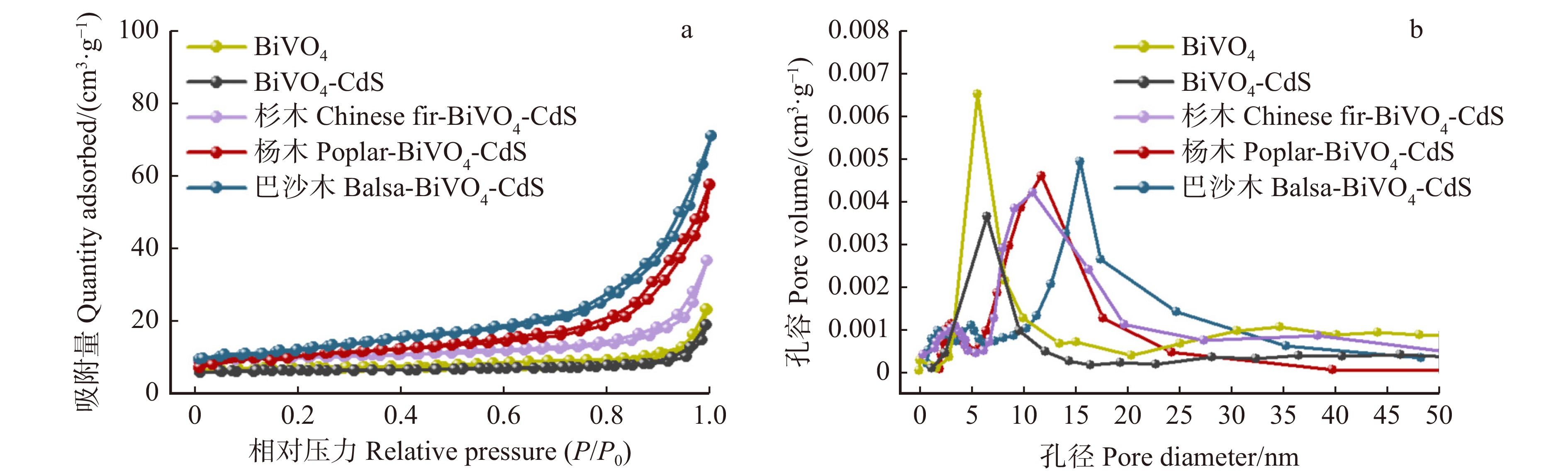
Table 2 Pore structure parameters of wood-templated BiVO4-CdS
样品 Sample 比表面积 Specific surface area/(m2·g−1) 孔径 Pore diameter/nm 孔容 Pore volume/(cm3·g−1) BiVO4 6.482 ± 1.326 6.038 ± 0.528 0.013 ± 0.004 BiVO4-CdS 7.116 ± 0.812 7.251 ± 0.457 0.024 ± 0.006 杉木 Chinese fir-BiVO4-CdS 11.760 ± 1.591 12.592 ± 1.793 0.041 ± 0.009 杨木 Poplar-BiVO4-CdS 18.484 ± 1.263 11.723 ± 1.154 0.072 ± 0.012 巴沙木 Balsa-BiVO4-CdS 28.091 ± 0.944 16.139 ± 1.696 0.088 ± 0.011
下载: 导出CSV
-
[1] 何盛, 吴再兴, 陈玉和, 等. 木(竹)材染色废水处理研究进展[J]. 竹子学报, 2016, 35(2): 58−62. doi: 10.3969/j.issn.1000-6567.2016.02.013 He S, Wu Z X, Chen Y H, et al. Progresses of waste water treatement for wood and bamboo dyeing[J]. Journal of Bamboo Research, 2016, 35(2): 58−62. doi: 10.3969/j.issn.1000-6567.2016.02.013
[2] Vlyssides A, Barampouti E M, Mai S, et al. Application of Fenton’s reagent on wastewater from a wood processing industry[J]. Environmental Engineering Science, 2008, 25(3): 327−332. doi: 10.1089/ees.2006.0283
[3] Doan T H Y, Chu T P M, Dinh T D, et al. Adsorptive removal of rhodamine B using novel adsorbent-based surfactant-modified alpha alumina nanoparticles[J]. Journal of Analytical Methods in Chemistry, 2020: 6676320.
[4] 李庆, 陈灵辉, 李丹, 等. 金属−有机骨架光催化降解染料的研究进展[J]. 纺织学报, 2021, 42(12): 188−195. Li Q, Chen L H, Li D, et al. Research progress in photocatalytic degradation of dyes using metal-organic frameworks[J]. Journal of Textile Research, 2021, 42(12): 188−195.
[5] Chandrabose G, Dey A, Gaur S S, et al. Removal and degradation of mixed dye pollutants by integrated adsorption-photocatalysis technique using 2-D MoS2/TiO2 nanocomposite[J]. Chemosphere, 2021, 279: 130467. doi: 10.1016/j.chemosphere.2021.130467
[6] 张雯, 张晗, 王觅堂. 钒酸铋光催化剂的制备及改性[J]. 材料科学与工程学报, 2022, 40(5): 1−12. doi: 10.14136/j.cnki.issn1673-2812.2022.05.027 Zhang W, Zhang H, Wang M T. Preparation and modification of bismuth vanadate photocatalyst[J]. Journal of Materials Science and Engineering, 2022, 40(5): 1−12. doi: 10.14136/j.cnki.issn1673-2812.2022.05.027
[7] Guo M N, Wang Y, He Q L, et al. Enhanced photocatalytic activity of S-doped BiVO4 photocatalysts[J]. RSC Advances, 2015, 72(5): 58633−58639.
[8] Wu Z S, Xue Y T, He X F, et al. Surfactants-assisted preparation of BiVO4 with novel morphologies via microwave method and CdS decoration for enhanced photocatalytic properties[J]. Journal of Hazardous Materials, 2020, 387: 122019. doi: 10.1016/j.jhazmat.2020.122019
[9] Xue Y T, Chen Z Y, Wu Z S, et al. Hierarchical construction of a new Z-scheme Bi/BiVO4-CdS heterojunction for enhanced visible-light photocatalytic degradation of tetracycline hydrochloride[J]. Separation and Purification Technology, 2021, 275: 119152. doi: 10.1016/j.seppur.2021.119152
[10] 李奕萱. 硫化镉改性材料最新光催化研究进展[J]. 黑龙江环境通报, 2019, 43(2): 86−89. doi: 10.3969/j.issn.1674-263X.2019.02.028 Li Y X. Recent progress in photocatalytic research of cadmium sulfide modified materials[J]. Heilongjiang Environmental Journal, 2019, 43(2): 86−89. doi: 10.3969/j.issn.1674-263X.2019.02.028
[11] Yang R J, Zhu R S, Fan Y Y, et al. In situ synthesis of C-doped BiVO4 with natural leaf as a template under different calcination temperatures[J]. RSC Advances, 2019, 9(25): 14004−14010. doi: 10.1039/C9RA01875A
[12] Wang M, Zheng H Y, Liu J, et al. Enhanced visible-light-driven photocatalytic activity of B-doped BiVO4 synthesized using a corn stem template[J]. Materials Science in Semiconductor Processing, 2015, 30: 307−313. doi: 10.1016/j.mssp.2014.09.031
[13] Liu Z T, Fan T X, Gu J J, et al. Preparation of porous Fe from biomorphic Fe2O3 precursors with wood templates[J]. Materials Transactions, 2007, 48(4): 878−881. doi: 10.2320/matertrans.48.878
[14] Liu Z T, Fan T X, Zhang W, et al. The synthesis of hierarchical porous iron oxide with wood templates[J]. Microporous and Mesoporous Materials, 2005, 85(1−2): 82−88. doi: 10.1016/j.micromeso.2005.06.021
[15] Fan H M, Wang D J, Liu Z P, et al. Self-assembled BiVO4/Bi2WO6 microspheres: synthesis, photoinduced charge transfer properties and photocatalytic activities[J]. Dalton Transactions, 2015, 44(26): 11725−11731. doi: 10.1039/C5DT01222H
[16] Wang D J, Shen H D, Guo L, et al. Design and construction of the sandwich-like Z-scheme multicomponent CdS/Ag/Bi2MoO6 heterostructure with enhanced photocatalytic performance in RhB photodegradation[J]. New Journal of Chemistry, 2016, 40(10): 8614−8624. doi: 10.1039/C6NJ01893A
[17] Cui L, Chang M Q, Chen J, et al. Judd-Ofelt analysis, photoluminescence and photocatalytic properties of core-shell SiO2@TiO2:Eu3+ nanospheres with different diameters[J]. Journal of Physics and Chemistry of Solids, 2018, 123: 162−171. doi: 10.1016/j.jpcs.2018.07.020
[18] Cao Q H, Xiao L, Li J, et al. Morphology-controlled fabrication of Ag3PO4/chitosan nanocomposites with enhanced visible-light photocatalytic performance using different molecular weight chitosan[J]. Powder Technology, 2016, 292: 186−194. doi: 10.1016/j.powtec.2016.02.003
[19] 郭宇, 李超, 李英洁, 等. 木材细胞壁与木材力学性能及水分特性之间关系研究进展[J]. 2019, 46(8): 14−18. Guo Y, Li C, Li Y J, et al. Research progress on the ralationship between wood cell wall and wood mechanical properties and moisture properties[J]. 2019, 46(8): 14−18.
[20] Zhou W J, Yin Z Y, Du Y P, et al. Synthesis of few-layer MoS2 nanosheet-coated TiO2 nanobelt heterostructures for enhanced photocatalytic activities[J]. Small, 2013, 9(1): 140−147. doi: 10.1002/smll.201201161
[21] Yang G, Chen D M, Ding H, et al. Well-designed 3D ZnIn2S4 nanosheets/TiO2 nanobelts as direct Z-scheme photocatalysts for CO2 photoreduction into renewable hydrocarbon fuel with high efficiency[J]. Applied Catalysis B-Environmental, 2017, 219: 611−618. doi: 10.1016/j.apcatb.2017.08.016
[22] 李洁. 多孔富缺陷半导体应用于光催化降解废水有机污染物[J/OL]. 材料导报, 2023 [2022−11−08]. http://kns.cnki.net/kcms/detail/50.1078.TB.20220727.1616.004.html. Li J. Porous defective semiconductor for photocatalytic degradation of organic pollution in wastewater[J/OL]. Materials Reports, 2023 [2022−11−08]. http://kns.cnki.net/kcms/detail/50.1078.TB.20220727.1616.004.html.
[23] da Silva A, Kyriakides S. Compressive response and failure of balsa wood[J]. International Journal of Solids and Structures, 2007, 44(25−26): 8685−8717.
-
期刊类型引用(20)
1. 林文月，王锦，张喆. 基于视觉吸引的森林景观色彩要素识别及影响因素研究——以云南轿子山自然保护区为例. 西部林业科学. 2024(02): 133-141 . 
百度学术
2. 刘帅健，邓华锋. 基于PSPNet深度学习网络景观要素语义分割的春季森林景观质量评价. 西北林学院学报. 2024(03): 231-238 . 百度学术
3. 尹佳仪，甘德欣. 长株潭绿心视觉美学质量及视觉异质性研究. 农业与技术. 2024(23): 93-98 . 百度学术
4. 郎博帅，刘叶凡，韩阳媚，欧阳嗣航，李玉灵，程顺. 林内色彩斑块分布格局对秋季生态景观林美景度的影响——以塞罕坝机械林场为例. 林业与生态科学. 2023(01): 98-105 . 百度学术
5. 陆子婧，王锦，张喆，刁秀丽，王钰，林文月. 植物色彩量化方法研究. 现代农业科技. 2022(02): 127-132 . 百度学术
6. 张菲，李玉灵. 塞罕坝机械林场生态景观林空间结构对夏季景观质量的影响. 林业与生态科学. 2022(02): 206-212+216 . 百度学术
7. 马薛骑，裘鸿菲，张群. 景观结构要素与色彩因子对滨水景观视觉质量的影响——以武汉东湖磨山景区为例. 西北林学院学报. 2022(03): 231-238+280 . 百度学术
8. 贾娜，史久西，秦一心，格日勒图，张龙. 森林色彩景观格局指数与色彩属性指标对观赏效应的影响. 林业科学. 2021(02): 12-21 . 百度学术
9. 贾娜，闫伟，史久西，格日乐图，车晓雨. 秋色叶树木树冠色彩特性对其观赏效应的影响. 林业科学. 2021(11): 37-48 . 百度学术
10. 钟姝，赵曜，李雄，姚朋. 基于SBE法的北京植物园月季园植物组群美学评价. 中国城市林业. 2020(01): 66-70 . 百度学术
11. 韩丽，马长乐. 基于SBE法的滨江公园美景度调查研究——以昆明市滨江公园为例. 江苏农业科学. 2020(10): 137-142 . 百度学术
12. 李雨薇，彭培好，汪平. 森林景观色彩研究进展. 四川林业科技. 2020(03): 153-160 . 百度学术
13. 赵凯，李金航，徐程扬. 侧柏人工林林分结构与色彩斑块间的耦合关系. 北京林业大学学报. 2019(01): 82-91 . 本站查看
14. 马冰倩，徐程扬，刘江，常成，赵凯，孔祥琦，龙嘉翼. 城镇森林视觉景观异质性对美学质量的影响. 浙江农林大学学报. 2019(02): 366-374 . 百度学术
15. 宋世杰，颜立红，颜玉娟，赖小连，雷佳伟. 基于SBE法的宅间植物景观美学评价研究. 中国城市林业. 2019(02): 17-21 . 百度学术
16. 曹瑜娟，徐程扬，崔义，岳阳，任雅雪. 观景距离和光照条件对黄栌林景观色彩的影响. 中南林业科技大学学报. 2019(05): 22-29+48 . 百度学术
17. 李苹，毛斌，许丽娟，吴鞠，刘海轩，徐程扬. 密度、灌草盖度和树干形态对油松人工风景林林内景观指数的影响. 北京林业大学学报. 2018(10): 115-122 . 本站查看
18. 马冰倩，徐程扬，崔义. 八达岭秋季景观整体色彩组成对美景度的影响. 西北林学院学报. 2018(06): 258-264 . 百度学术
19. 王子，荣媛，李明阳，钱春花. 森林景观色彩评价研究. 世界林业研究. 2017(03): 41-45 . 百度学术
20. 张喆，郄光发，王成，姜莎莎. 多尺度植物色彩表征及其与人体响应的关系. 生态学报. 2017(15): 5070-5079 . 百度学术
其他类型引用(15)
计量
- 文章访问数: 564
- HTML全文浏览量: 132
- PDF下载量: 70
- 被引次数: 35
