Numerical simulation of neutral axis in transverse bending of tree trunk
-
摘要:目的
为了评估树木的风载安全性，研究树木在风力作用下的横力弯曲，确定树干横截面形状、树轮、缺陷等因素对树干弯曲中性轴的影响。
方法采用欧拉–伯努利梁假设，推导了通用弯曲中性轴倾斜角计算公式。随后设计了树干模型，模型包括3种外轮廓（圆形、椭圆形、随机形状）和两种内部结构（多层同心、圆形缺陷），并采用不同的弹性模量模拟材料属性的变化。最后进行数值模拟，采用随机森林算法分析、预测数值模拟的结果，确定各个因素的重要性。
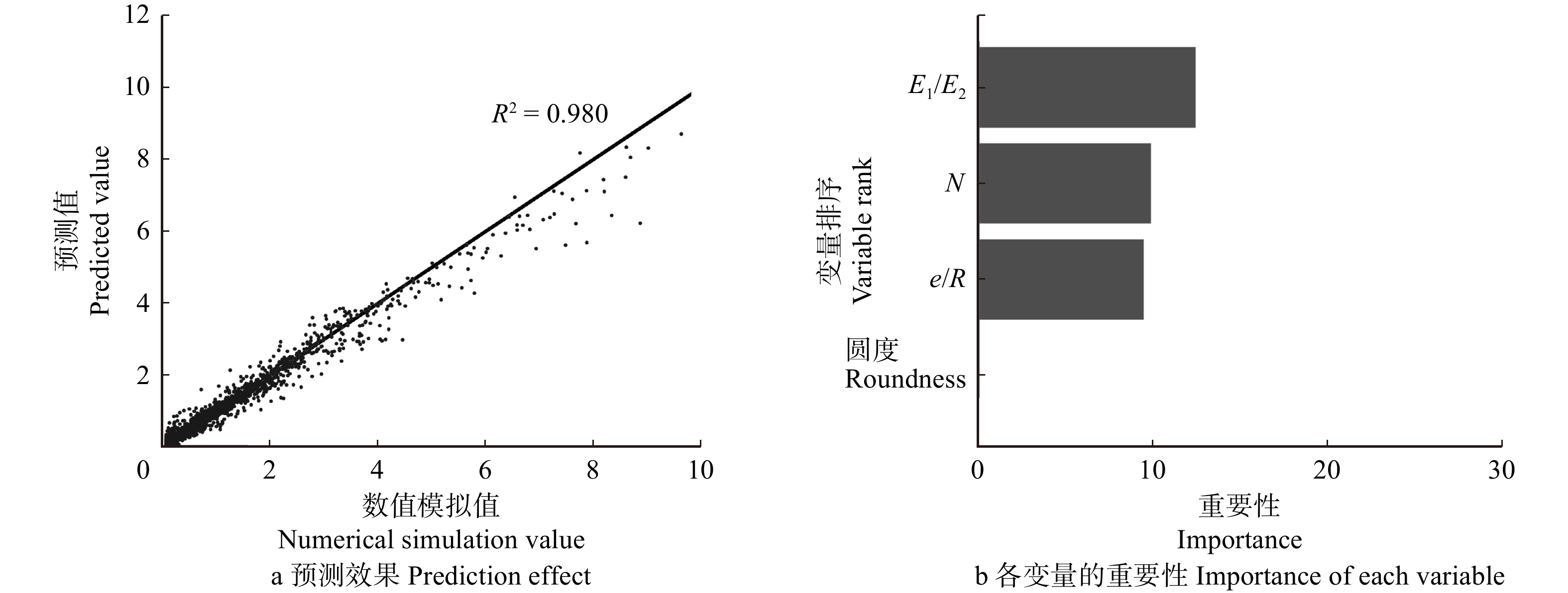
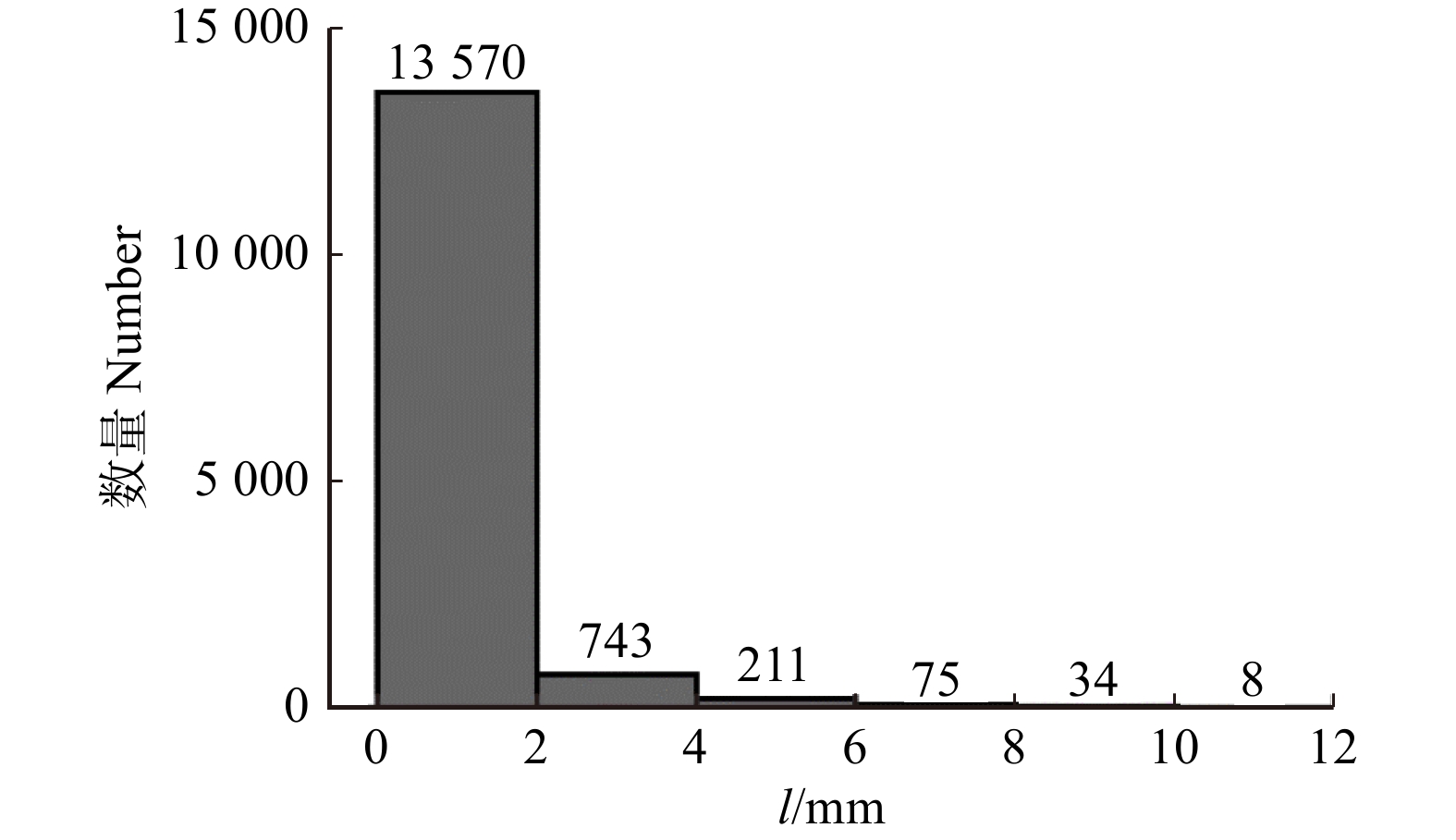
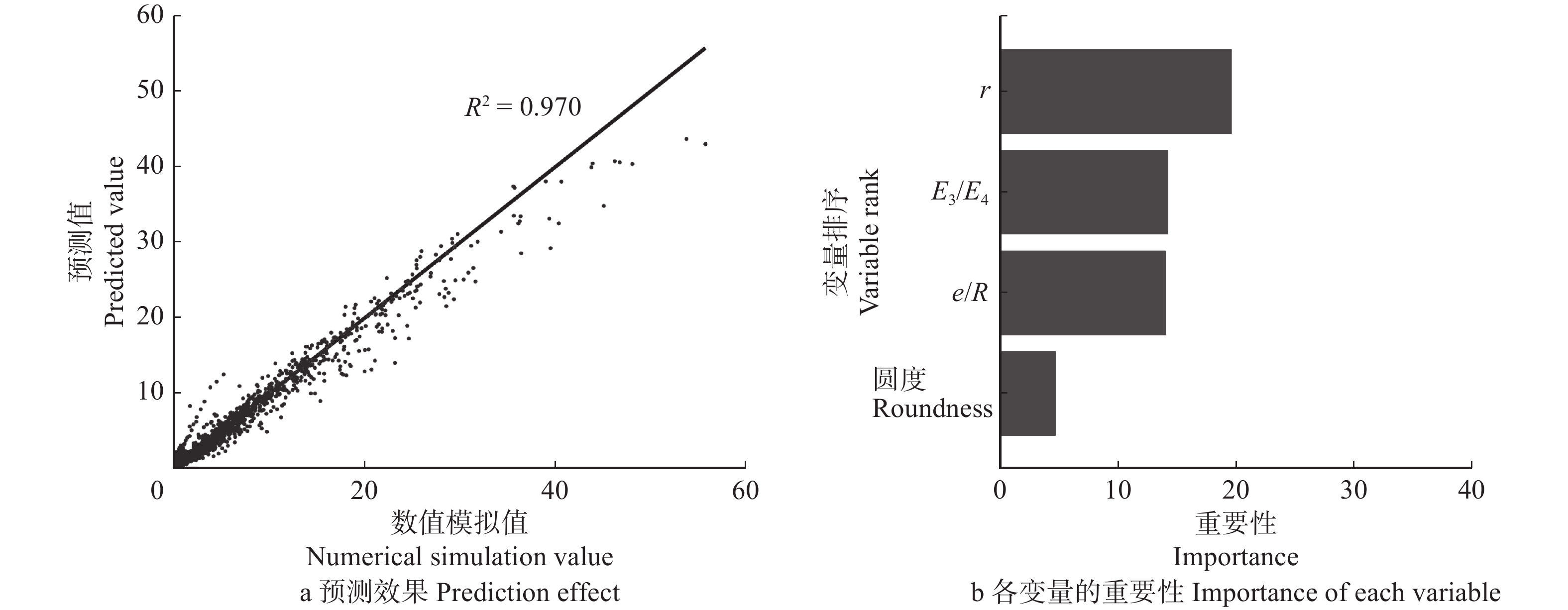
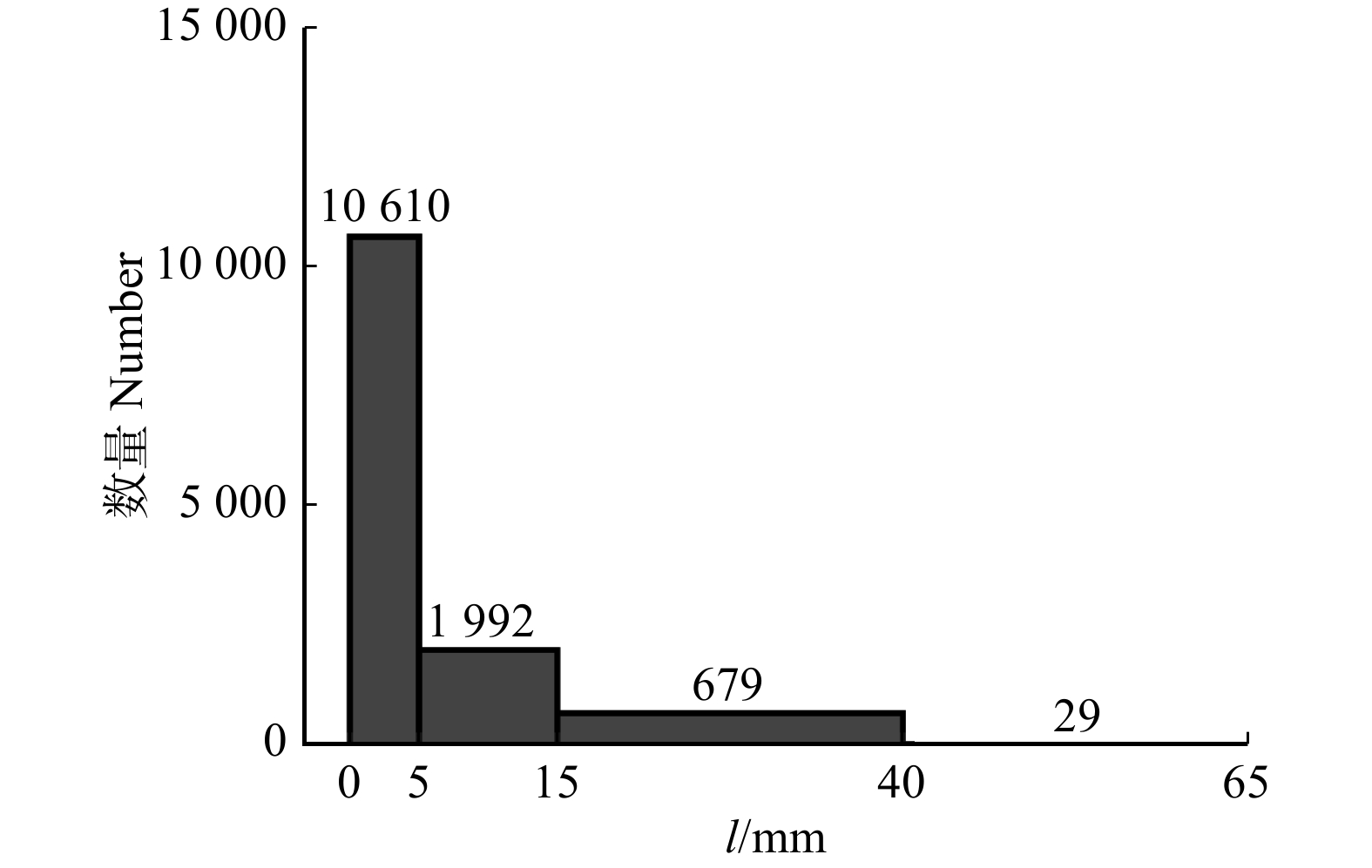
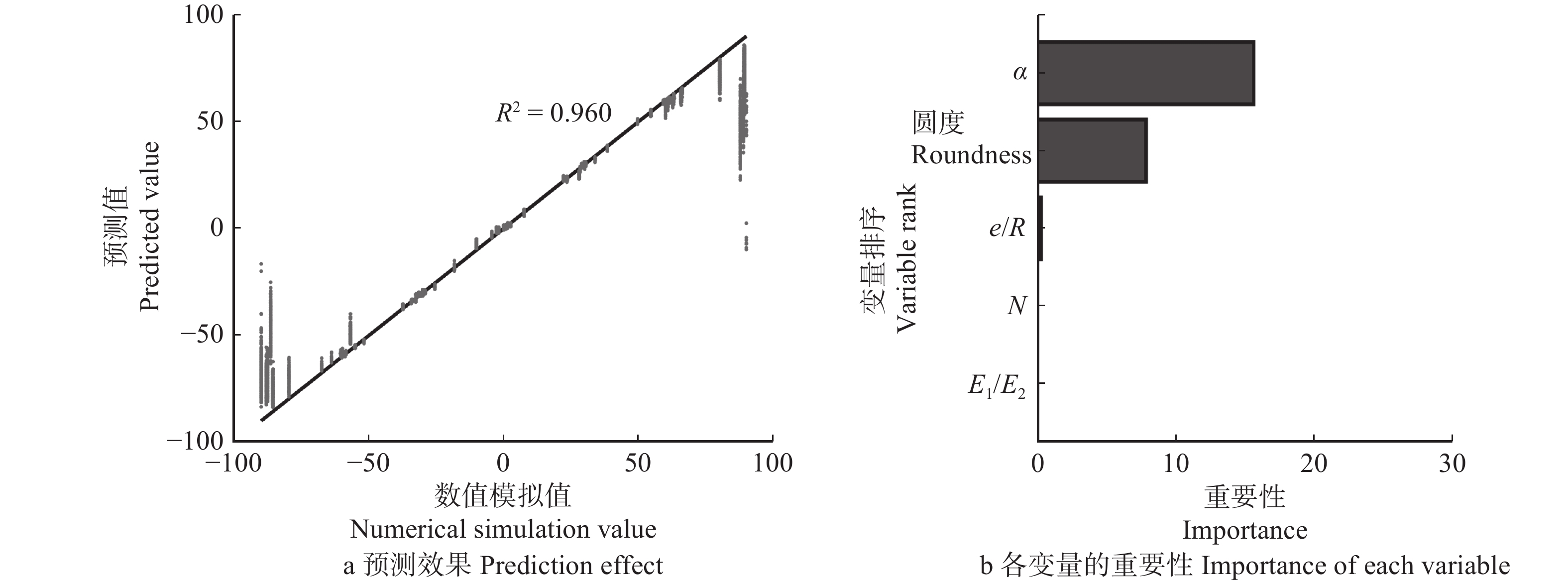
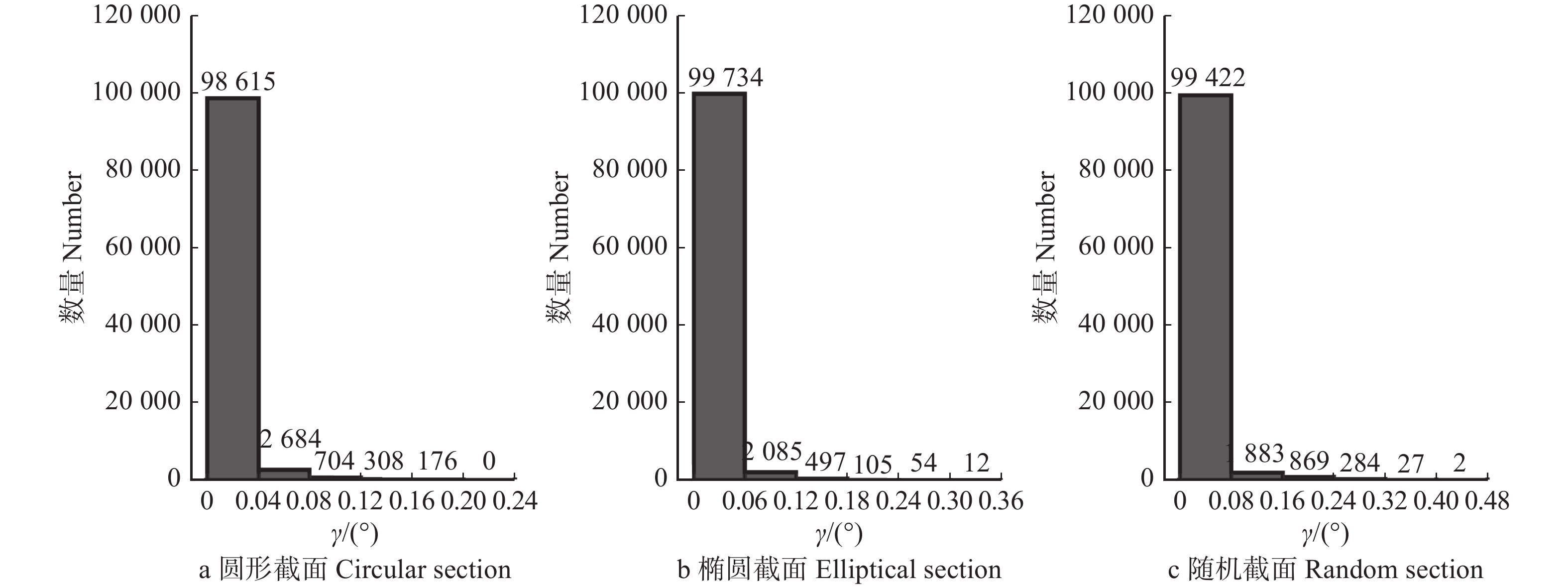
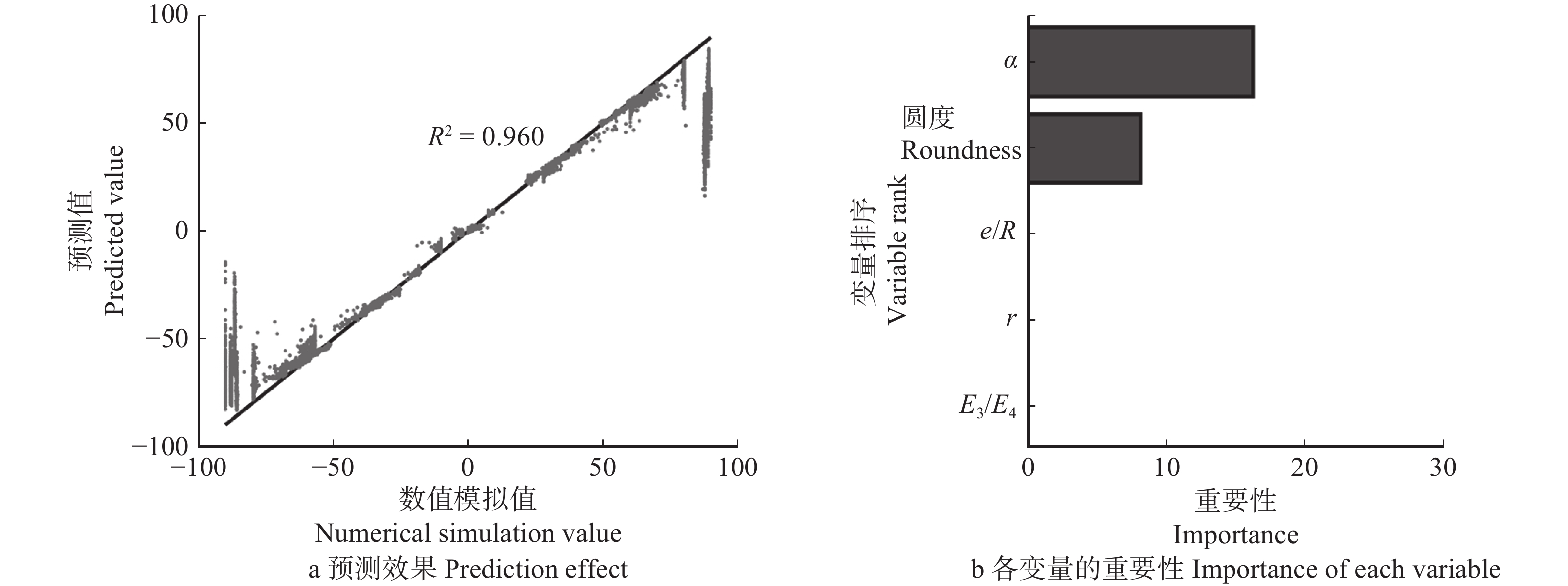
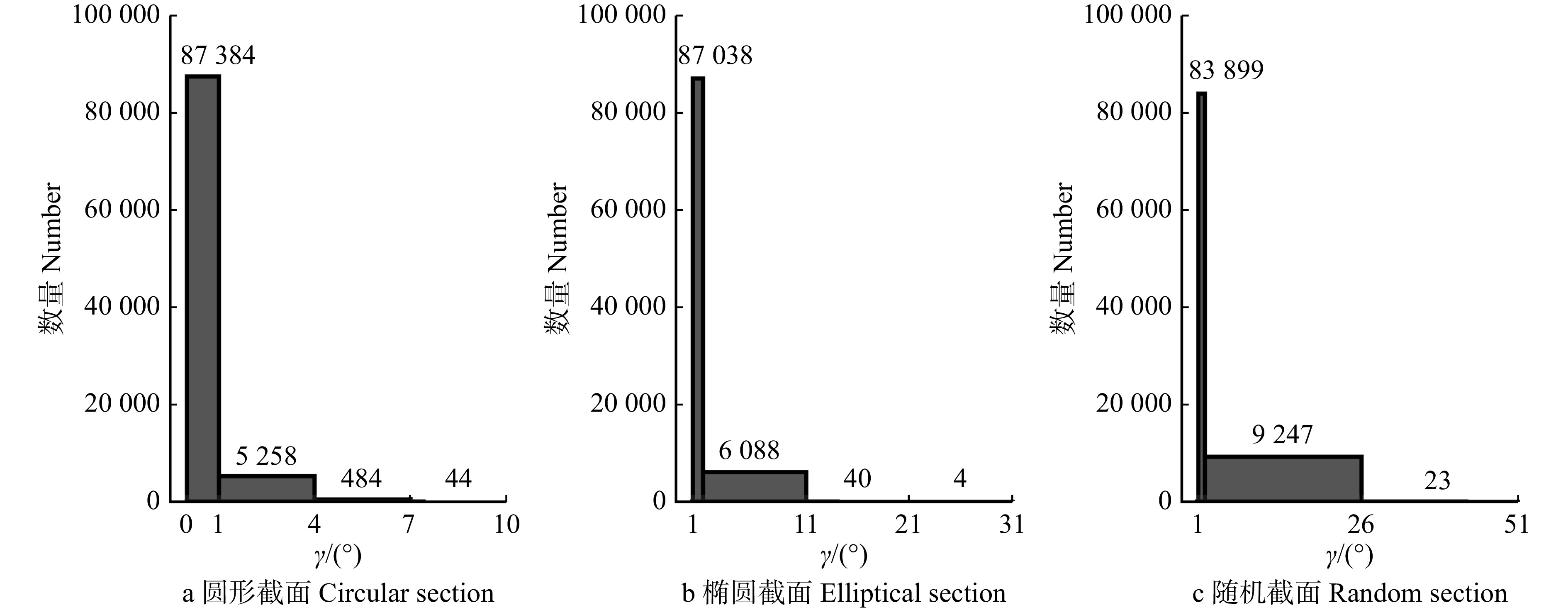
结果在树轮模型中，质形偏心距 < 4 mm的比例超过97%，各因素影响质形偏心距的重要性为早晚材弹性模量比 > 树轮数量 > 偏心距与基圆半径之比 > 截面圆度；偏转角（实际弯曲中性轴倾斜角相对均匀截面弯曲中性轴倾斜角的偏转角）均 < 0.5°，且< 0.08°的比例高于97%，影响树干弯曲中性轴倾斜角的重要性为载荷方位角 > 截面圆度 > 偏心距与基圆半径之比 > 树轮数量 > 早晚材弹性模量比。在缺陷模型中，质形偏心距 < 5 mm的数量约占总数的80%，在5 ~ 15 mm之间的约为15%，> 15 mm的约为5%，各因素影响质形偏心距的重要性为缺陷半径 > 缺陷树干与正常树干弹性模量之比 > 偏心距与基圆半径之比 > 截面圆度；偏转角 < 1°的比例超过90%，但在极限情况下偏转角也可达到50°，影响弯曲中性轴倾斜角的重要性为载荷方位角 > 截面圆度 > 偏心距与基圆半径之比 > 缺陷半径 > 缺陷树干与正常树干弹性模量之比。
结论树轮对树干弯曲中性轴的影响很小，横截面轮廓形状、缺陷对其影响较大。在进行树干受力检测计算时，可忽略树轮的影响，但要考虑树干横截面形状和缺陷的影响。
Abstract:ObjectiveIn order to assess the wind load safety of trees, the transverse force bending of trees under wind force was studied to determine the effect of factors such as trunk cross-sectional shape, tree ring, and defects on the neutral axis of trunk bending.
MethodIn this study, the Euler-Bernoulli beam assumption was used to deduce a generalized formula for the slope of neutral axis. Then, trunk models were designed with three types of contours (circle, ellipse, and random), two internal structures (multi-layer concentric structure and circular defects). And different moduli of elasticity were used to simulate variations in material properties. Finally, numerical simulations were performed, the results of numerical simulations were analyzed and predicted using the random forest model, and the relative contribution of each factor was identified.
ResultIn tree-ring models, the probability that the distance from mass center to form center of the tunk cross-section was less than 4 mm exceeded 97%, and the importance affecting the distance was ratio of the elasticity modulus of the early wood to the late wood > tree-ring number > ratio of the eccentricity distance to the basal circle radius > cross-section roundness. The deflection angles (from the actual neutral axis to the neutral axis of uniform section) were all less than 0.5°, and more than 97% of the total number was less than 0.08°. The importance affecting the slope angle of neutral axis in trunk bending was load azimuth > cross-section roundness > ratio of the eccentricity distance to the basal circle radius > tree-ring number > ratio of the elasticity modulus of the early wood to the late wood. In the circular defect model, there was about 80% of all cases where the distance from mass center to form center was less than 5 mm, about 15% of all cases between 5−15 mm, and about 5% of all cases greater than 15 mm. The importance affecting the distance was the defect radius > ratio of the elasticity modulus of the trunk with defects to the normal trunk > ratio of the eccentricity distance to the basal circle radius > cross-section roundness. More than 90% of all cases had a deflection angle less than 1°, but in some extreme cases, the deflection angle may reach 50°. The importance affecting the slope angle was load azimuth > cross-section roundness > ratio of the eccentricity distance to the basal circle radius > the defect radius > ratio of the elasticity modulus of the trunk with defects to the normal trunk.
ConclusionTree-ring have a small effect on bending neutral axis of a tree trunk, while defects and cross-section shapes have a large effect on it. In the calculation and detection of trunk stress, the tree-ring can be ignored, but the cross-section shape and defects inside a trunk need to be taken into account.
-
人造板用甲醛系胶黏剂在生产和使用过程中释放出游离甲醛，危害人体健康。聚氨酯类、大豆蛋白、木质素、淀粉等无醛胶黏剂可以有效解决人造板甲醛释放问题，但存在生产成本高、工艺复杂等问题，限制了其应用范围。地质聚合物作为一种新型的无机胶黏剂，有效地解决了甲醛释放的问题，并且具有低成本、高耐热、耐久性好、绿色环保等优势，有望替代甲醛系胶黏剂[1]。地质聚合物是由铝氧四面体和硅氧四面体组成的三维立体网状结构的无机聚合物，通常由高岭土、粉煤灰等工业固废物经碱激发制备而成，偏高岭土是由高岭土在高温（600 ~ 900 ℃）经脱水形成的无水硅酸铝，碱激发后的偏高岭土具有优异的力学性能与耐久性能等，可用于制备胶凝材料。有研究发现地质聚合物基胶黏剂在热压作用下会渗透到木材细胞壁和细胞腔中，通过机械互锁作用与木材相连以实现胶合作用[2]，但作为木材胶黏剂，地质聚合物存在无机胶黏剂与木材界面相容性差等共性缺点，导致胶接强度较低，限制其进一步推广应用。有研究通过有机掺杂提高地质聚合物性能，聚氨酯掺杂对性能影响不大[3]，酚醛树脂掺杂提高了胶黏剂强度，但存在甲醛释放问题[4]。
环氧树脂固化体系中有活性极大的环氧基、羟基等极性基团，具有胶接强度高、力学性能好、收缩率小、绿色环保等特点，常用于混凝土加固、木质素胶黏剂改性等[5−6]。有学者发现环氧树脂掺杂到地质聚合物中可以填充孔隙和优化孔隙结构，两者之间形成的氢键作用增强了基体的韧性[7]。因此，本研究以偏高岭土为地质聚合物原料，以环氧树脂作为有机掺杂剂，以聚醚胺为固化剂，以γ-氨丙基三乙氧基硅烷为偶联剂，经碱激发、有机掺杂制备地质聚合物基胶黏剂，研究不同有机物质掺杂对地质聚合物胶黏剂性能的影响。
1. 材料与方法
1.1 材 料
偏高岭土购于上海昊弗化工有限公司，采用X射线荧光光谱仪测试其氧化物组分（表1）；液体硅酸钠（Na2SiO3）购于江苏省无锡市亚泰联合化工有限公司，模数为2.13；氢氧化钠（NaOH，纯度≥96%）颗粒购于天津市永大化学试剂有限公司；环氧树脂E51（环氧值0.5）购于北京科奥科技有限公司；聚醚胺固化剂购于中山金诚黏合剂有限公司；γ-氨丙基三乙氧基硅烷（KH550）购于上海迈瑞尔化学技术有限公司；杨木单板购于山东省菏泽市，幅面为400 mm × 400 mm，厚度为1.5 mm。
表 1 偏高岭土的氧化物成分Table 1. Oxide compositions of biotite kaolinite成分 Component SiO2 Al2O3 TiO2 Fe2O3 P2O5 Na2O CaO 其他 Others 质量分数 Mass fraction 50.778% 44.703% 2.641% 0.634% 0.491% 0.206% 0.169% 0.378% 1.2 胶黏剂与胶合板的制备
1.2.1 胶黏剂的制备
制备8 mol/L的氢氧化钠溶液，根据式（1）计算所需碱激发剂模数对应的硅酸钠溶液和氢氧化物溶液的体积，将上述两种溶液混合均匀后，静置24 h待用。
n=w0w=aρwn0/62aρw/62+bc/2000 (1) 式中：n为碱激发剂模数1.7；w0为二氧化硅的质量分数，%；w为氧化钠的质量分数，%；ρ为硅酸钠溶液的密度，g/mL；n0为工业水玻璃模数；a为硅酸钠溶液的体积，mL；b为氢氧化物溶液的体积，mL；c为硅酸钠溶液的体积，mL。
将碱激发剂与偏高岭土混合，高速剪切搅拌120 s（纯地质聚合物G），依次加入环氧树脂（E）、聚醚胺固化剂（C）、硅烷偶联剂KH550（S）制备不同物料配比（质量比）的胶黏剂，具体参数见表2。
表 2 环氧树脂掺杂地质聚合物胶黏剂的物料配比（质量比）Table 2. Material ratios of epoxy resin doped geopolymer adhesive (mass ratio)编号 No. 物料配比 Material ratio G A∶B = 10∶15 GE A∶B∶E = 10∶15∶1.60 GC A∶B∶C = 10∶15∶0.32 GEC A∶B∶E∶C = 10∶15∶1.28∶0.32 GECS3 A∶B∶E∶C∶S = 10∶15∶0.62∶0.16∶0.129 GECS6 A∶B∶E∶C∶S = 10∶15∶1.28∶0.32∶0.134 GECS9 A∶B∶E∶C∶S = 10∶15∶1.99∶0.50∶0.138 GECS12 A∶B∶E∶C∶S = 10∶15∶2.74∶0.69∶0.143 注：A代表偏高岭土，B代表碱激发剂，C代表聚醚胺固化剂，E代表环氧树脂，S代表硅烷偶联剂KH550。Notes: A represents metakaolin, B represents alkali-activator, C represents polyether amine curing agent, E represents epoxy resin, and S represents silane coupling agent KH550. 1.2.2 地质聚合物胶合板的制备
将杨木单板裁切为幅面200 mm × 200 mm × 1.5 mm的规格，单板施胶为量300 g/m2，采用相邻层纹理垂直的方法将单板热压为三层胶合板，热压工艺为压力1.2 MPa、时间260 s、温度150 ℃。
1.3 胶黏剂性能表征
1.3.1 化学结构表征
将从胶合板胶层部分刮取的胶黏剂粉末使用玛瑙研钵粉碎至200目，使用X射线光电子能谱仪（Thermo Kalpha，美国 Thermo 公司）对样品进行分析，辐射源为Al-Kα，结合能相对于C1s峰在284.8 eV进行校正。
使用傅里叶变换衰减全反射红外光谱仪（Nicolet iS5，赛默飞世尔科技公司）对干燥后的样品粉末测试，分析不同物质掺杂导致的化学结构变化，光谱范围500 ~ 4 000 cm−1，分辨率为4 cm−1，采集次数为32次。
1.3.2 流变性、凝结时间与热稳定性测试
使用旋转流变仪（HAAKE Roto Viscol，德国）匀变速剪切模式在室温下测试现配胶黏剂的黏度，剪切速率为1 ~ 60 s−1，时间为1 min，取100个数据。使用恒速变温模式测试胶黏剂在升温过程中的流动性，剪切速率为30 s−1，温度范围为30 ~ 100 ℃，时间为8 min，取100个数据。
将现配的胶黏剂置于模具中，参照GB/T 1346—2011《水泥标准稠度、凝结时间、安定性检验方法》测试凝结时间，其中初凝针距底板（4 ± 1） mm时，记为初凝时间。
使用热重分析仪（STA200，日本日立HITACHI）对样品热稳定性进行表征，温度范围30 ~ 800 ℃，加热速率10 ℃/min，测试氛围使用氮气气流。
1.4 胶合板性能检测
1.4.1 胶合强度测试
根据GB/T 17657—2022《人造板及饰面人造板理化性能试验方法》中Ⅱ类胶合板的要求进行测试，将放置3天的胶合板试件放入63 ℃恒温水浴中浸泡3 h，取出试件后在室温下放置10 min后，用微机控制人造板万能力学试验机（WDW-E，济南耐而试验机有限公司）测试湿态胶合强度和干态胶合强度，测试时均匀加载，加载速率5 mm/min，直至胶合试件发生剪切破坏，记录最大载荷数值，根据式（2）计算胶合强度。
X=PS (2) 式中：X为胶合强度，MPa；P为最大载荷数值，N；S为受剪切面的面积，S = 625 mm2。
1.4.2 胶合界面形貌和阻燃性能测试
采用扫描电子显微镜（Regulus 8100，日本日立公司）表征水热处理后胶合板的胶合界面结构形貌。
采用锥形量热仪（i-Cone，英国FTT公司）测试地质聚合物基杨木试件的阻燃性能，测试方法参考ISO 5660-1:2015《Reaction-to-fire tests—heat release，smoke production and mass loss rate—part 1：Heat release rate (cone calorimeter method) and smoke production rate （dynamic measurement）》。采用7层胶合板，并加工成100 mm × 100 mm × 10 mm规格尺寸，测试热辐射强度为50 kW/m2。
1.4.3 甲醛释放量测试
根据GB/T 17657—2022《人造板及饰面人造板理化性能试验方法》中干燥器法测定胶合板的甲醛释放量，评价胶合板的环保性能。测试时，将9个胶合板样品（150 mm × 50 mm × 10 mm）放在装有300 mL蒸馏水玻璃结晶皿的密闭干燥器中24 h，用乙酰丙酮分光光度计法测定吸收液在波长412 nm处的吸光度。
2. 结果与分析
2.1 地质聚合物基胶黏剂的化学结构分析
图1a、b显示：在掺杂环氧树脂与聚醚胺胶黏剂浆体（GEC）的N1s分峰拟合图中位于398.0 eV的峰是C−N，浆体中N来源仅有聚醚胺，并且相较于未掺杂环氧树脂的浆体（GC），掺杂环氧树脂与聚醚胺浆体的C−N峰面积上升了78.57%。这表明聚醚胺中的氨基与环氧树脂的环氧键反应，形成了更多的C−N[8]。
![]()
图 1 XPS谱图的N1s和Si2p分峰拟合结果a、b分别为GEC、GC的N1s谱图，c ~ f分别为G、GE、GEC、GECS6的Si2p谱图。a and b are N1s spectra of GEC and GC, respectively. c−f are Si2p spectra of G, GE, GEC, and GECS6, respectively.Figure 1. Results of N1s and Si2p split peak fitting of XPS spectra图1c ~ f显示：环氧树脂、聚醚胺添加并不会对Si−OH的峰值及面积产生较大影响；GECS6的Si2p分峰拟合图中位于102.1和102.9 eV的峰分别是Si−O−T（T为Si或Al）和Si−OH，相比于未掺杂硅烷偶联剂的胶黏剂（GEC），GECS6中占据主导地位的Si−O−T峰面积从75.2%下降到50.4%，而Si−OH的相对含量从24.8%上升至49.6%，表明硅烷偶联剂水解后生成的硅醇基团与地质聚合物骨架结构成功结合，起到有机–无机之间的桥接作用[4]。
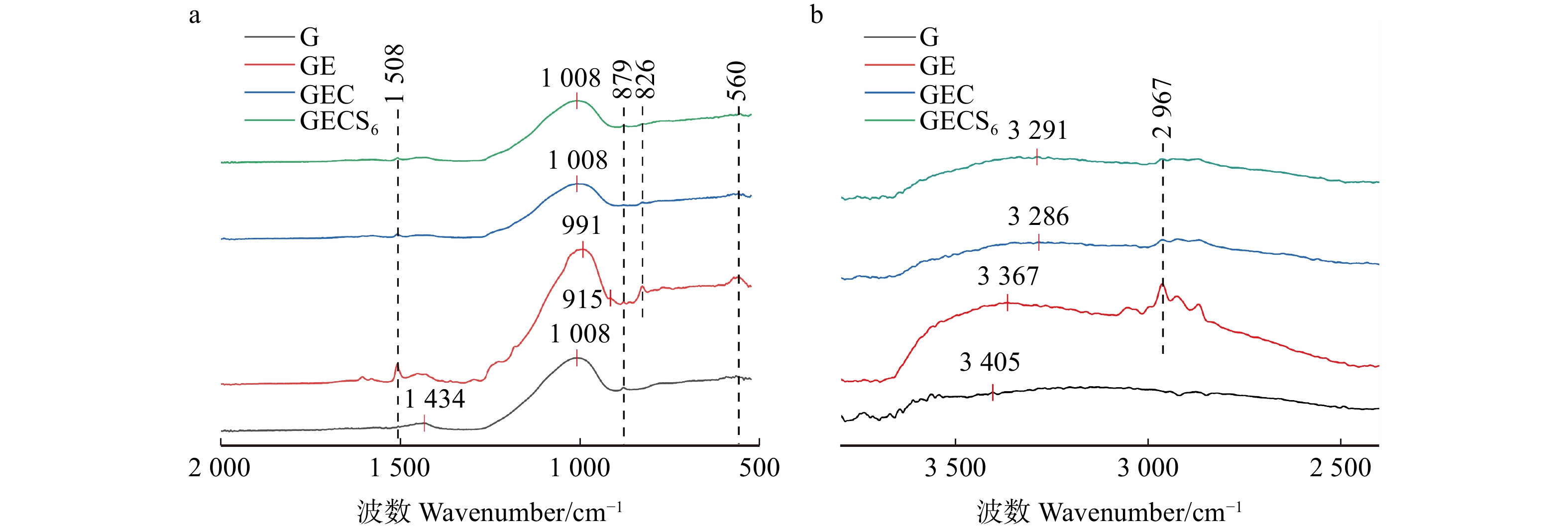
图2显示：在3 100 ~ 3 600 cm−1是−OH的特征峰，加入环氧树脂与聚醚胺后峰值向波数低的方向移动，表明生成了更多的Si−OH，验证了XPS的检测结果，并且说明了环氧树脂与地质聚合物末端羟基、KH550水解有机羟基存在较强的氢键结合[9]；地质聚合物的主峰出现在1 008 cm−1处，由地质聚合物中的Si−O−T的不对称伸缩振动造成的[10]，仅加入环氧树脂后峰值向波数低的方向移动，可能是端基环氧环的加入导致的[11]；在915 cm−1处为环氧环的特征峰，加入固化剂和偶联剂后峰消失，表明环氧键与氨基发生反应，形成交联结构[12]。
![]()
图 2 G、GE、GEC、GECS6的衰减全反射红外光谱图Figure 2. Attenuated total reflectance infrared spectra of G, GE, GEC, GECS62.2 地质聚合物基胶黏剂浆体的黏度与凝结时间
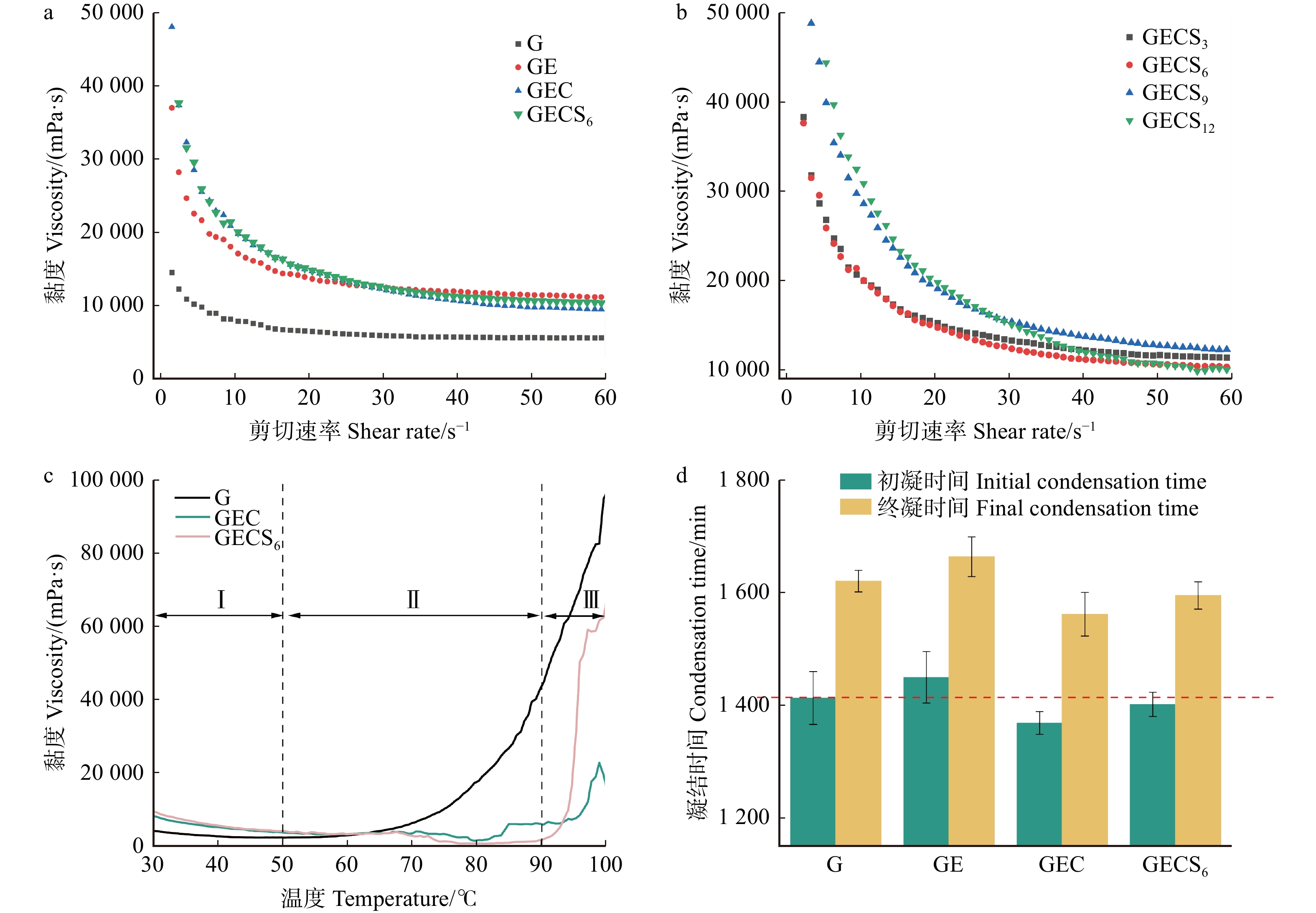
地质聚合物浆体是一种假塑性流体，在稳态的剪切作用下，流体黏度随剪切速率的升高而降低，保持“剪切变稀”的流体特性[13]，环氧树脂的加入并不会改变这种特性（图3a）；随着环氧树脂质量分数的增加，地质聚合物基浆体初始黏度会增大，但在高剪切速率下浆体黏度相差不大（图3b）。胶黏剂浆体的黏度会影响板材施胶的均匀性以及板材性能，因此制备的地质聚合物胶黏剂在施胶过程中需要不断地搅拌，确保浆体时刻处于低黏度状态。
![]()
图 3 不同物质掺杂对胶黏剂黏度的影响（a），不同环氧树脂浓度对胶黏剂黏度的影响（b），不同温度对胶黏剂黏度的影响（c），不同物质掺杂对胶黏剂凝结时间的影响（d）Figure 3. Effects of different substance doping on adhesive viscosity (a), effects of different epoxy resin concentrations on adhesive viscosity (b), effects of different temperatures on adhesive viscosity (c), and effects of different substance doping on condensation time (d)图3c显示：在第Ⅰ阶段30 ~ 50 ℃，浆体黏度逐渐变小，符合地质聚合物剪切变稀规律；在第Ⅱ阶段50 ~ 90 ℃，地质聚合物浆体黏度逐渐变大，并且变化速率加快，这是升温促成的三维网络结构形成，浆体聚合程度高[14]，而环氧树脂、聚醚胺和硅烷偶联剂的掺杂导致黏度拐点从50 ℃延长至90 ℃，可能是有机物质掺杂阻隔了地质聚合物间反应，延缓了地质聚合物胶黏剂固化并导致黏度增加[15]；在第Ⅲ阶段90 ~ 100 ℃，掺杂硅烷偶联剂的胶黏剂浆体黏度上升速率明显快于其他有机物，可能是因为高温加快了硅烷偶联剂与地质聚合物的反应，胶黏剂固化速率提高[16]。
图3d显示：环氧树脂的加入会增加浆体的凝结时间，这是由于环氧树脂阻碍了地质聚合物间的反应；在加入聚醚胺固化剂后，环氧树脂固化速度加快[17]，交联网络开始形成，因此凝结时间减少；硅烷偶联剂加入后，硅烷与地质聚合物水化产物的耦合作用使得聚合物分子进一步吸附到水化产物上，使得反应延缓，因此凝结时间增大[9]。
2.3 地质聚合物基胶黏剂的热稳定性
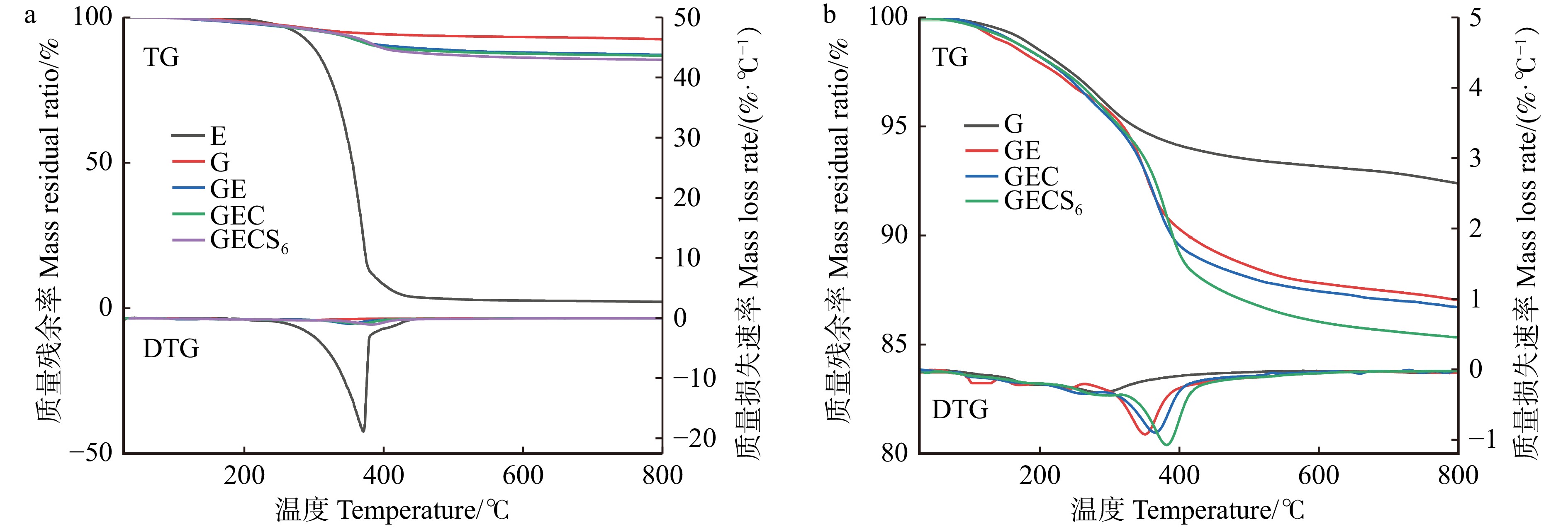
图4显示有机物质掺杂均会不同程度地降低胶黏剂的稳定性。第一个热降解阶段（100 ~ 200 ℃），环氧树脂和地质聚合物质量损失率相近，环氧树脂是由羟基的脱水引起的[18]，并且此温度下胺类固化剂上的氮原子容易被热氧化破坏，地质聚合物是由于其孔隙中游离水、吸着水的去除引起的[19]。第二个热降解阶段（200 ~ 450 ℃），环氧树脂大量热解是由于290 ℃时其分子中的聚合物主链破裂引起的快速分解[18]，聚醚胺和硅烷偶联剂的加入均使得DTG峰值向右偏移（图4b），表明两种物质均会与地质聚合物和环氧树脂形成更为致密的交联网络，抑制水分的散失[19]；地质聚合物在280 ℃的峰值归因于C−S−H凝胶的脱水[20]。第三个热降解阶段（400 ~ 800 ℃），地质聚合物较稳定的降解归因于方解石中水分的散失[21]。
![]()
图 4 地质聚合物基胶黏剂热重分析曲线a. E、G、GE、GEC、GECS6的TG与DTG曲线 TG vs. DTG curves of E, G, GE, GEC and GECS6；b. G、GE、GEC、GECS6的TG与DTG曲线 TG vs. DTG curves of G, GE, GEC and GECS6Figure 4. Thermogravimetric analysis curves of geopolymers-based adhesives2.4 地质聚合物基胶合板胶合性能分析
2.4.1 胶合界面
图5显示：水热处理后的纯地质聚合物胶合板中地质聚合物基体较为疏松，存在较大裂缝，地质聚合物和胶层之间存在明显开裂；而环氧树脂、聚醚胺与硅烷偶联剂掺杂后，地质聚合物基体结构致密，胶接界面连续且开裂较少。这是因为硅烷偶联剂水解产生Si−OH与地质聚合物形成化学结合，并与环氧树脂和木材形成致密的氢键，形成了多元复合和多键结合的“有机–无机”网络结构，增强了胶黏剂与木材间的界面附着力。
![]()
图 5 水热处理后胶合板胶合界面的微观形貌a. 纯地质聚合物基胶合板Pure geopolymer-based plywood； b. 环氧树脂掺杂地质聚合物基胶合板Epoxy-doped geopolymer-based plywoodFigure 5. Microscopic morphology of the gluing interface of plywood after hydrothermal treatment2.4.2 胶合强度
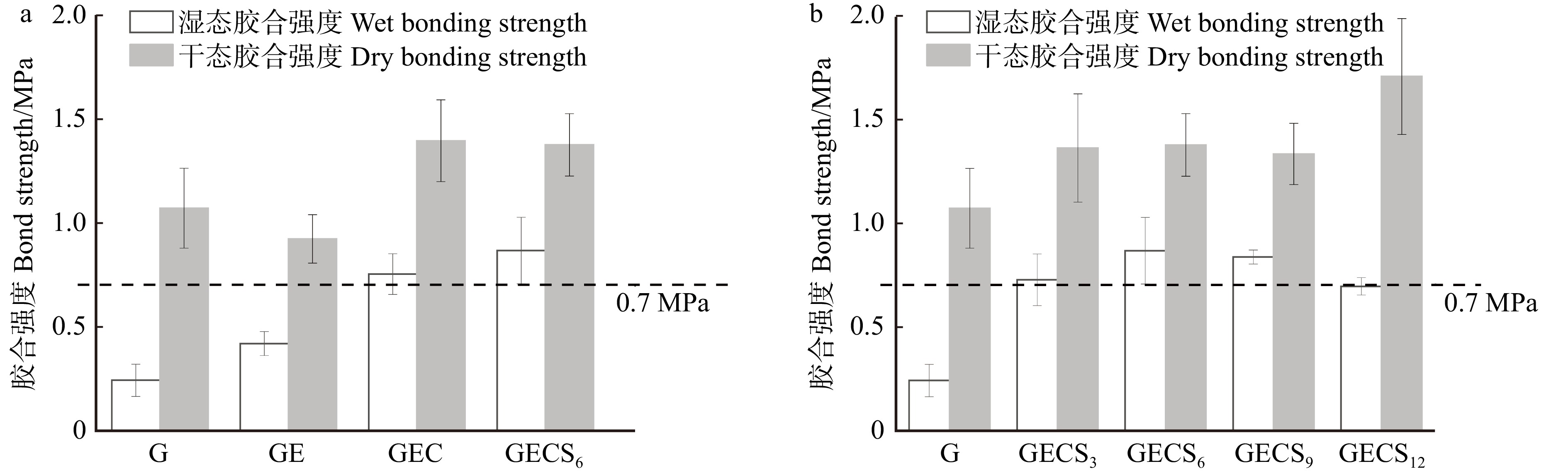
图6显示：纯地质聚合物（G）的湿态胶合强度最低值为0.25 MPa，有机物质掺杂均会不同程度地提高胶合板的胶合强度，环氧树脂（GE）、聚醚胺固化剂（GEC）和硅烷偶联剂（GECS6）掺杂后胶合强度较纯地质聚合物分别提高了64%、160%和248%；当环氧树脂和聚醚胺的质量分数分别为4.8%和1.2%（GECS6）时，胶合板的湿态胶合强度达到较优值0.87 MPa，因此该工艺参数较优。有机掺杂剂与地质聚合物通过化学键合，提高了胶合强度，但当环氧树脂质量分数超过4.8%时，过量树脂会阻碍地质聚合反应，影响地质聚合物的性能，导致板材强度下降[22]。
![]()
图 6 不同物料配比对地质聚合物基胶合板性能的影响a. 不同物质掺杂对胶合板性能的影响Effects of different substance doping on plywood properties；b. 不同质量分数的环氧树脂对胶合板性能的影响Effects of epoxy resins with different mass fractions on plywood propertiesFigure 6. Effects of different material ratios on geopolymer-based plywood properties2.5 地质聚合物基胶合板阻燃性能分析
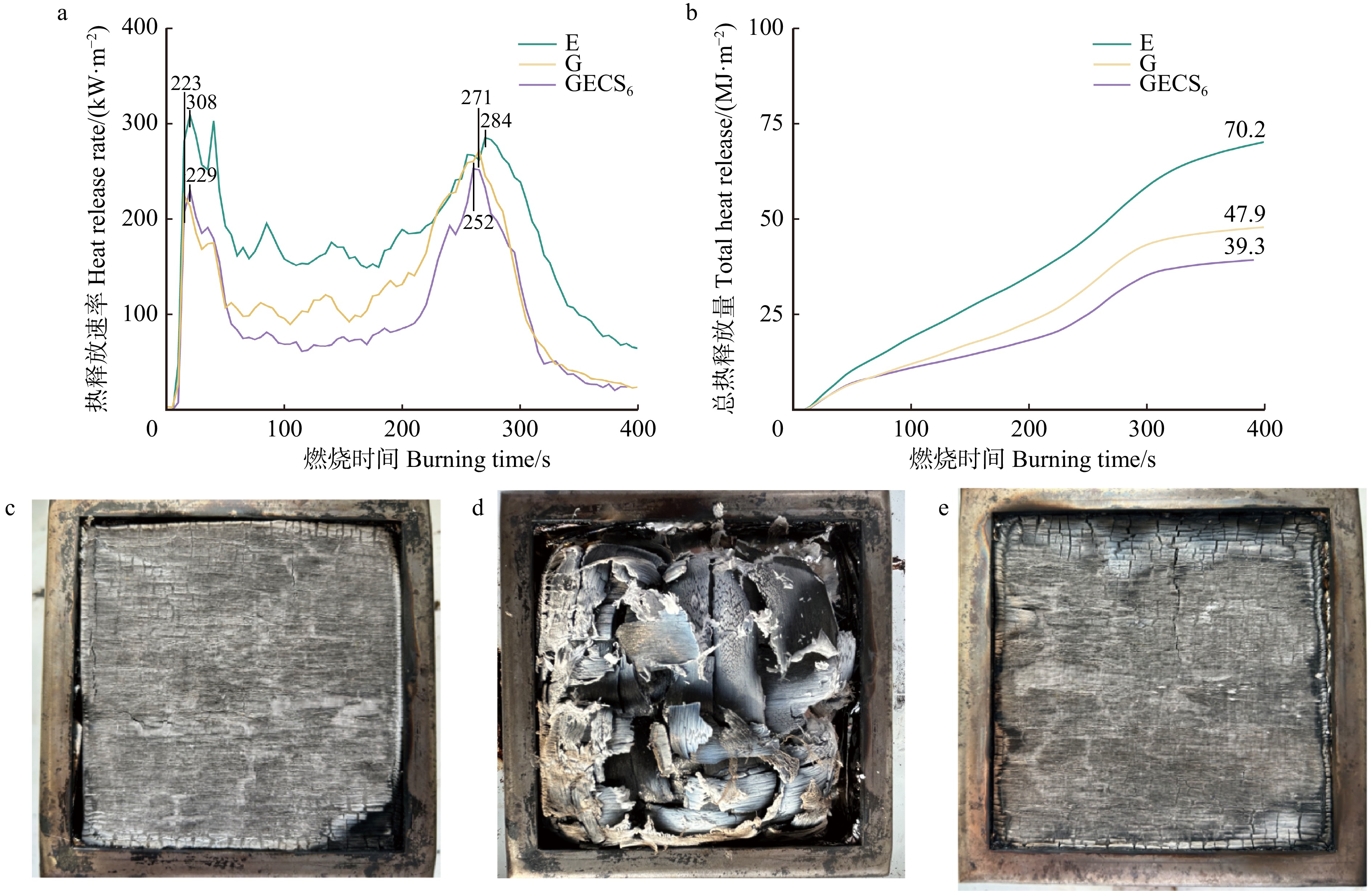
图7a，b显示：相较于纯地质聚合物，掺杂硅烷偶联剂GECS6胶合板的第二热释放速率峰值和总热释放量分别降低了7.01%和17.95%，阻燃性能得到一定程度的提高。图7c ~ e显示：纯地质聚合物胶合板和掺杂硅烷偶联剂组的胶合板均能保持较为完整的状态。这是由于地质聚合物渗透到木材内部，通过包裹部分纤维防止木材直接燃烧，地质聚合物结构中Al−O键和Si−O键热分解需要比C−C键更多的能量，氧化物（Al2O3）等的存在促进纤维素、半纤维素和木质素等有机物质在低温下的裂解，在燃烧初期更容易形成炭层，这些炭层有效地隔绝了氧气，并且胶合板中的含N固化剂和硅烷偶联剂在高温下会分解产生N2等不燃气体，稀释氧气浓度，在加热时形成保护层，进一步抑制燃烧[23−24]。
![]()
图 7 热释放速率（a）、总热释放量（b）曲线，地质聚合物基胶合板（c）、环氧树脂基胶合板（d）和复合胶黏剂基胶合板（e）燃烧后残骸Figure 7. Heat release rate (a) and total heat release (b) curve, post-combustion debris of geopolymer-based plywood (c), epoxy resin-based plywood (d) and composite adhesive-based plywood (e)2.6 地质聚合物基胶合板甲醛释放量
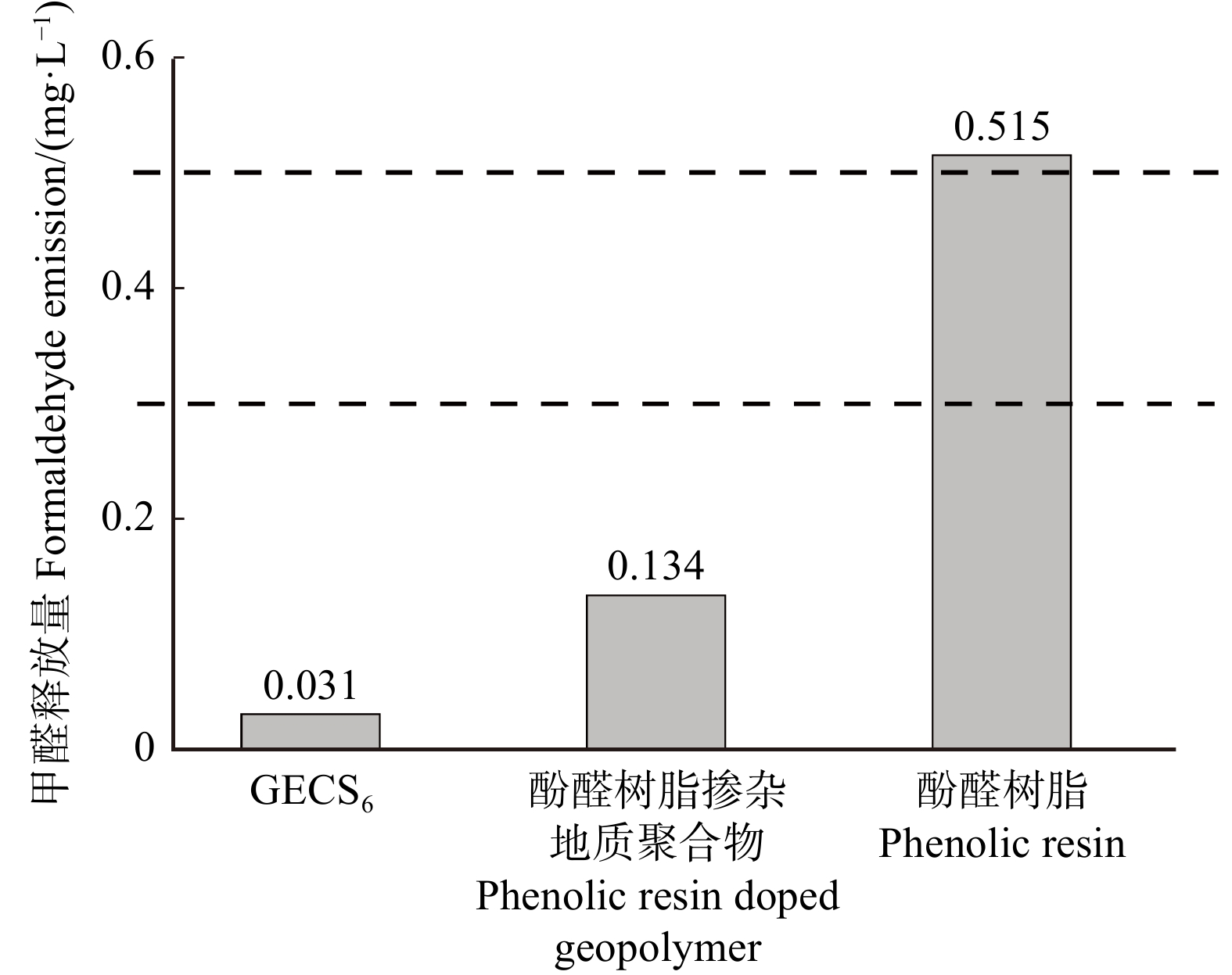
环氧树脂掺杂地质聚合物基胶合板的甲醛释放量为0.031 mg/L（图8），远低于酚醛树脂掺杂地质聚合物基胶合板（0.134 mg/L）和纯酚醛树脂基胶合板（0.515 mg/L）。参照日本人造板制品环保标准JIS A 5908:2015《Particleboards》，环氧树脂掺杂地质聚合物基胶合板的甲醛释放量满足最高环保标准F☆☆☆☆（甲醛释放量 ≤ 0.3 mg/L），环保性能优良。
![]()
图 8 GECS6和PF树脂基胶合板的甲醛释放量Figure 8. Formaldehyde emission from GECS6 and PF resin-based plywood2.7 环氧树脂掺杂地质聚合物木材胶黏剂增强机理
2.7.1 纯地质聚合物木材胶黏剂的胶接机理
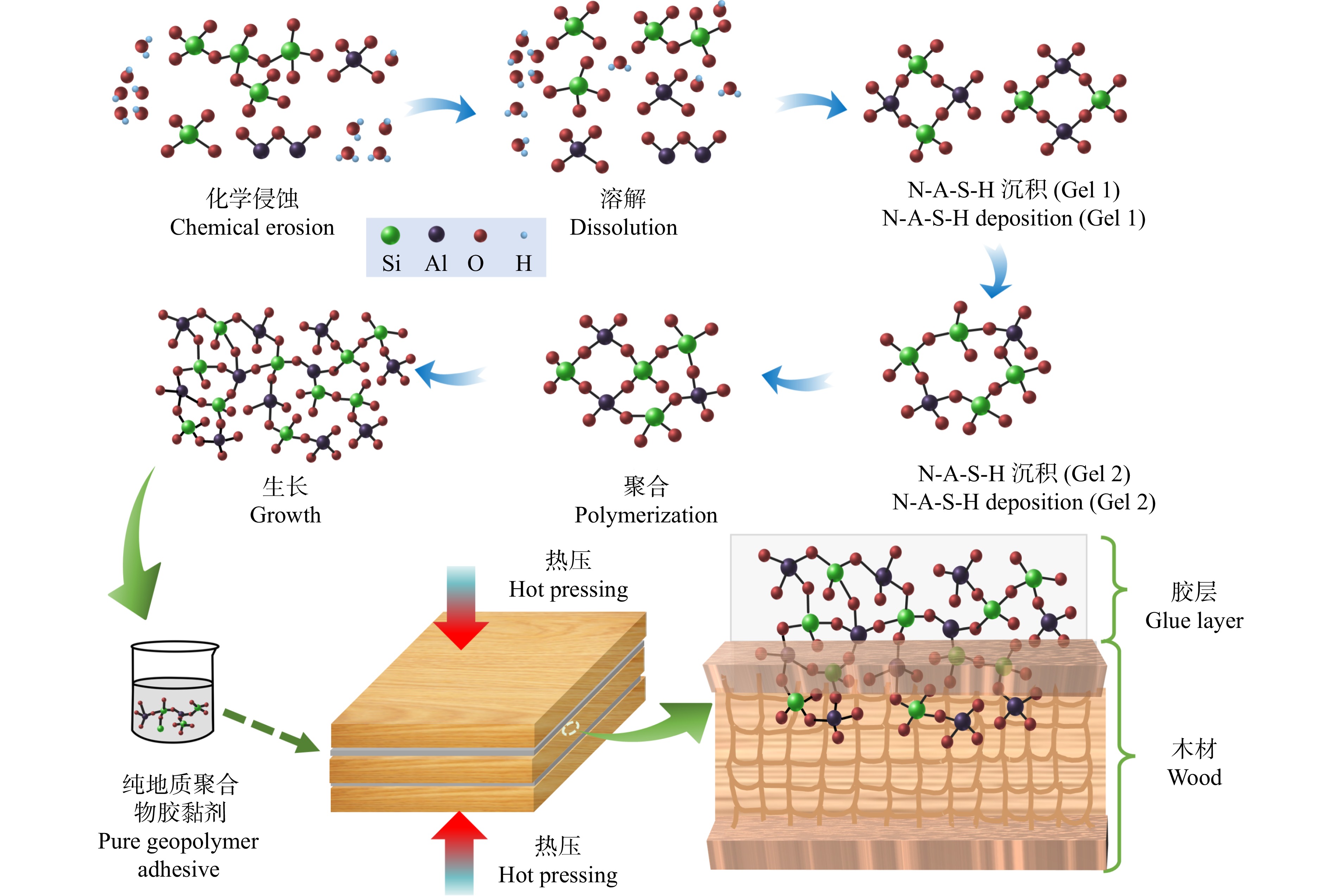
地质聚合物的形成以及与木材胶黏剂的胶接机理如图9所示。在高碱性的条件下，硅铝表面逐渐溶解，随着硅四面体和铝四面体单体的结合，形成硅铝交替的四面体的环结构（Gel 1和Gel 2），少量新生成的产物填充孔隙，最终形成无定形碱硅酸铝凝胶为主的地质聚合物[25−26]。由于碱的存在，地质聚合物会降解木材表面，并在压力作用下渗透到木材细胞壁和细胞腔中，形成类似“铆钉”结构的机械互锁连接以及较弱的氢键结合，从而在界面上加固木材[2]。
2.7.2 环氧树脂掺杂对地质聚合物木材胶黏剂的增强机理
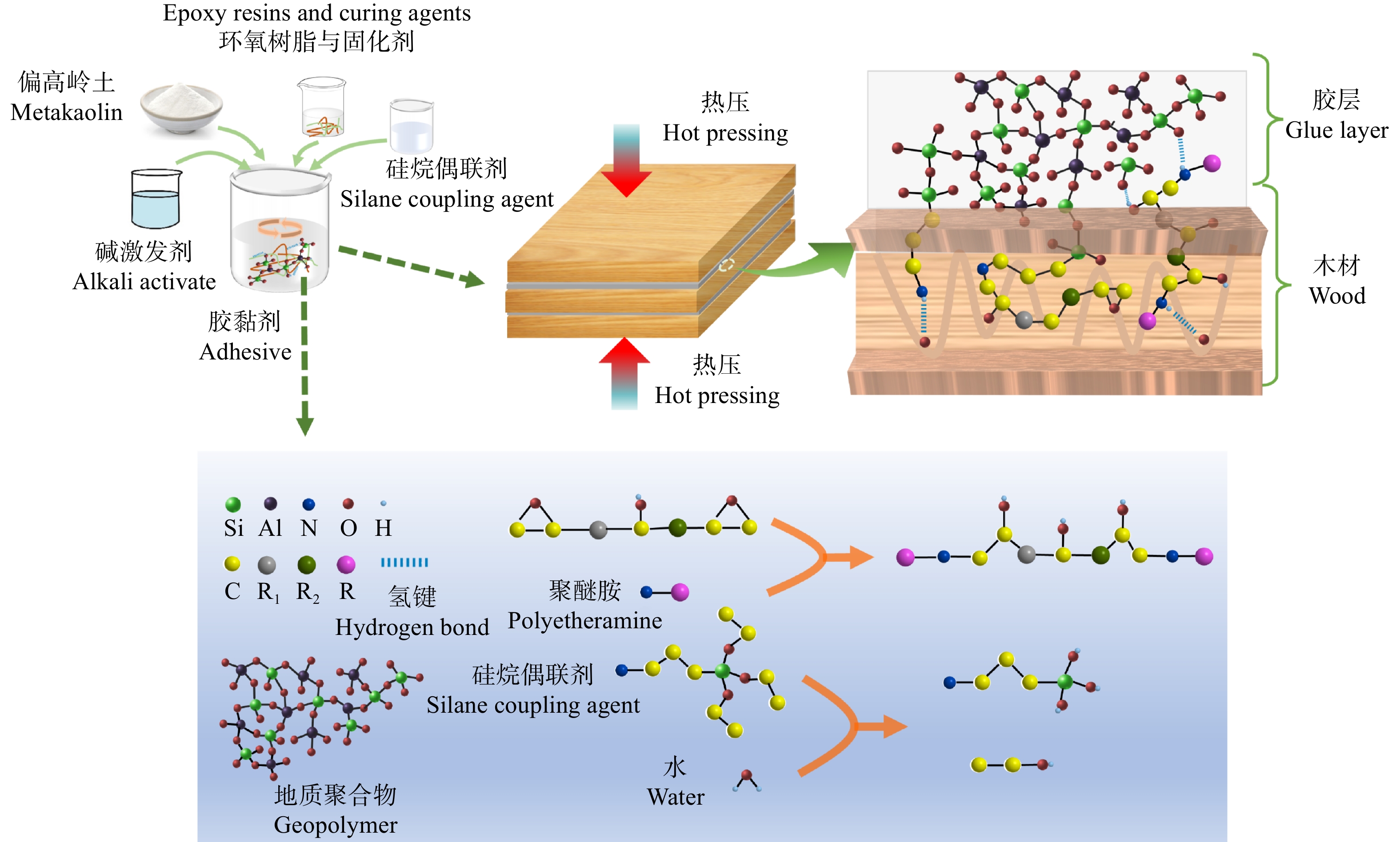
综上分析，可以总结出如图10所示的环氧树脂掺杂对地质聚合物木材胶黏剂增强机理。第一阶段，铝硅酸盐前驱体与碱激发剂进行地质聚合反应，在热压条件下形成地质聚合物空间网络，同时硅烷偶联剂水解暴露出羟基[27]，环氧树脂与聚醚胺和部分硅烷偶联剂KH550发生开环反应[16]。第二阶段，地质聚合物逐渐形成硅氧四面体和铝氧四面体，硅烷偶联剂中的Si−OH与地质聚合物中的Si相连形成Si−O−Si[9,27]，硅烷偶联剂将有机环氧树脂与无机地质聚合物通过化学键相连，并且开环后的环氧树脂与地质聚合物、硅烷偶联剂形成密集的氢键连接，体系结构不断完善，形成致密的有机–无机网络结构[4]。第三阶段，在热压作用下，部分胶黏剂渗透到木材内部，胶层表面的环氧树脂、地质聚合物通过氢键与木材相连，在胶层体系不断完善的过程中，胶层与木材结合更为紧密，逐渐形成了多元复合与多键结合的“有机–无机”网络结构。
![]()
图 10 环氧树脂掺杂对地质聚合物木材胶黏剂的增强机制Figure 10. Enhancement mechanism of epoxy resin doping on geopolymer wood adhesives3. 结 论
本研究以环氧树脂为有机掺杂剂，以偏高岭土基地质聚合物为主体，通过FTIR、XPS、旋转流变仪分析有机物质掺杂对胶黏剂浆体性能的影响，通过SEM-EDS和锥形量热仪分析3种物质对板材胶合强度、阻燃性能的影响，具体结论如下。
（1）地质聚合物基胶黏剂黏度符合“剪切变稀”的变化规律，当环氧树脂和聚醚胺的质量分数分别为4.8%和1.2%（GECS6）时，浆体黏度较低，有利于均匀施胶；与纯地质聚合物相比，有机物质掺杂会不同程度地降低胶黏剂浆体的热稳定性。
（2）环氧树脂杂化地质聚合物胶黏剂具有优异的胶合性能、阻燃性能和环保性能。GECS6胶合板的胶合强度为较优值（0.87 MPa），相比于纯地质聚合物胶黏剂提高了248%；较纯地质聚合物GECS6胶合板的第二热释放速率峰值和总热释放量基胶合板分别降低了7.01%和17.95%，阻燃性能得到了一定的提升；GECS6胶合板的甲醛释放量为0.031 mg/L，满足F☆☆☆☆标准。
（3）硅烷偶联剂水解生成的Si−OH与地质聚合物末端羟基反应形成Si−O−Si键，环氧树脂在聚醚胺作用下环氧环打开，并通过氢键与地质聚合物形成致密结构，提高了地质聚合物胶黏剂的胶接性能。
本研究采用环氧树脂改性地质聚合物木材胶黏剂，有效地提高了胶黏剂地胶合性能和阻燃性能，为制备高性能的环保型胶黏剂和胶合板提供理论依据，产品可用于建筑、家具以及交通工具等领域。
-
![]()
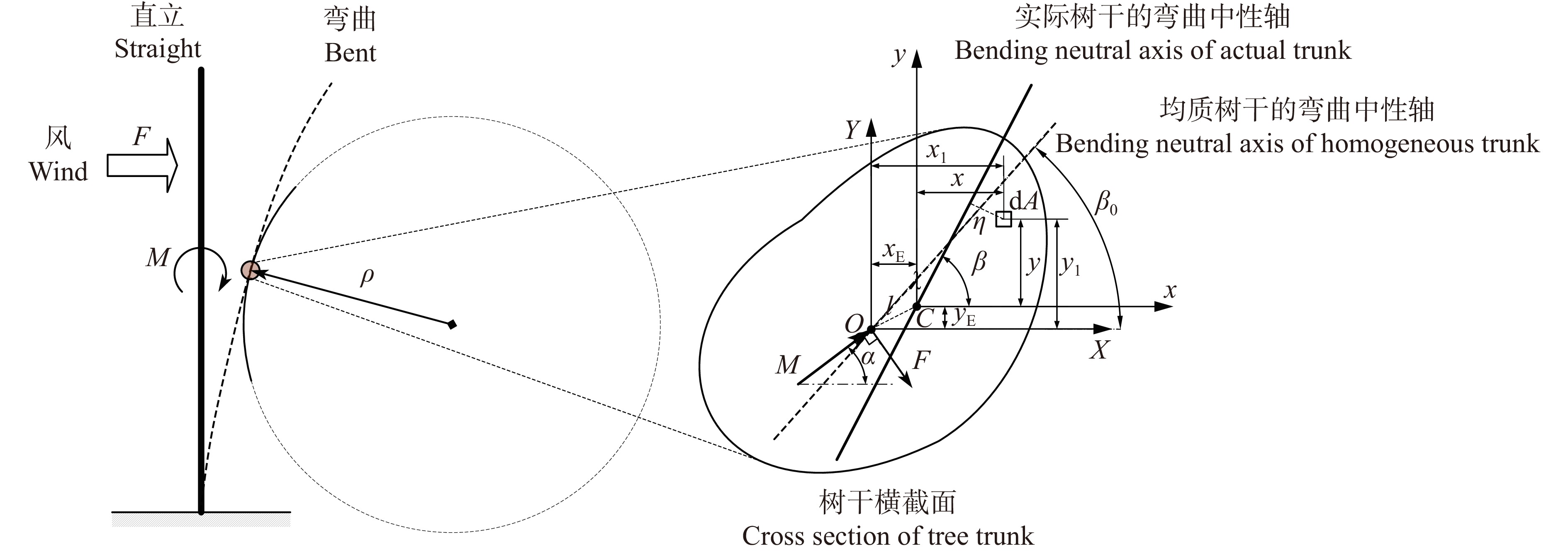
图 1 树干横截面受力示意图
F为风力，M为横截面上的弯矩，ρ为横截面处的曲率半径，O为横截面外轮廓形心，C为弯曲中性轴定点（质心），l为点O、C之间的距离（质形偏心距），α为载荷方位角，β为实际树干弯曲中性轴与x轴的夹角，β0为均质树干弯曲中性轴与x轴的夹角，任意微元dA到中性轴的距离为η。F is wind force, M is bending moment on cross section, ρ is radius of curvature at cross section, O is centre of cross-section,s external profile, C is fixed point of bending neutral axis, l is the distance between O and C, α is the load azimuth, β is angle between neutral axis of actual trunk and the x-axis, β0 is angle between neutral axis of homogenous trunk and x-axis, and η is the distance from any micromeric element dA to neutral axis.
Figure 1. Schematic diagram of cross-sectional stress on tree trunk
![]()
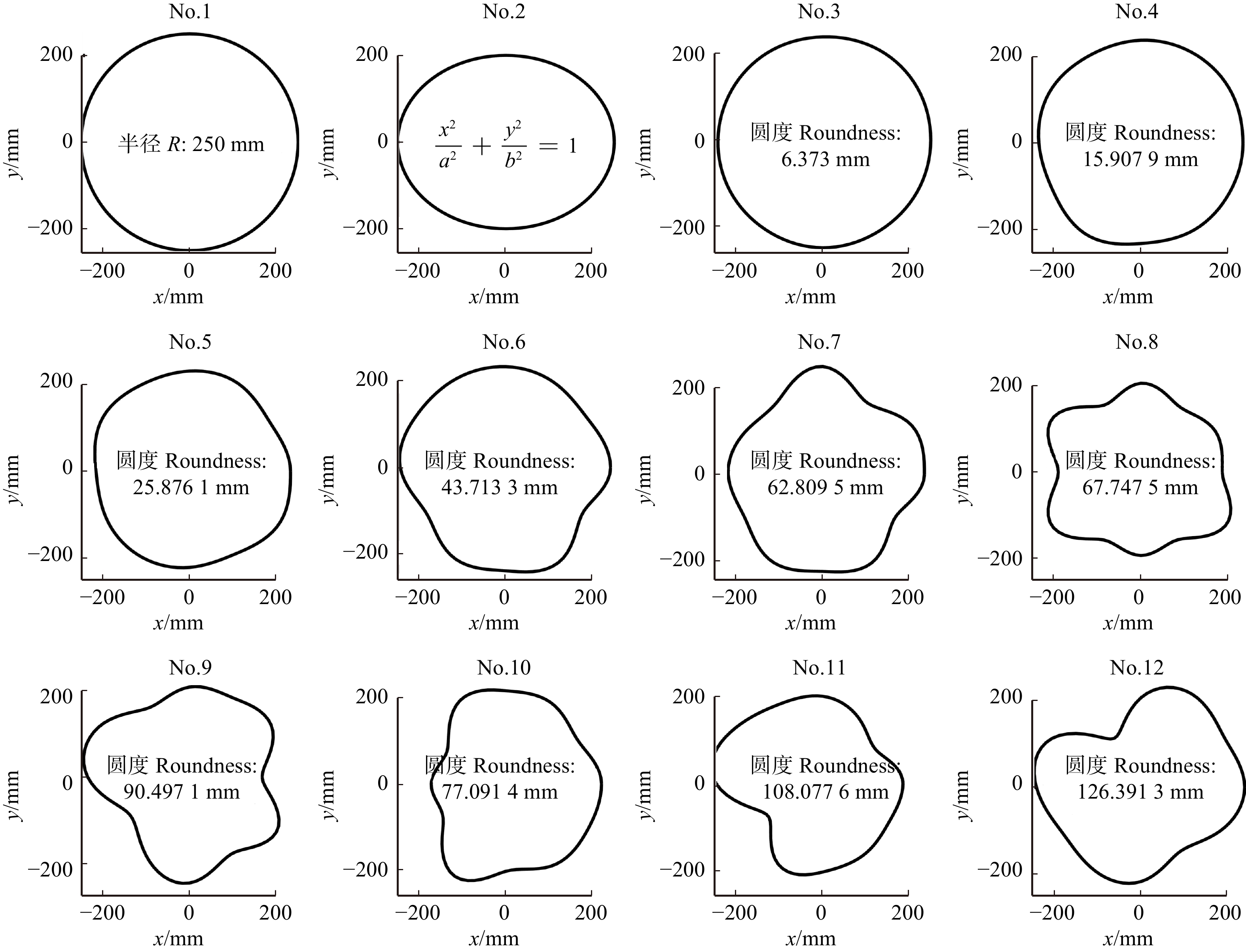
图 2 树干模型横截面形状
No. 1为圆形横截面，No. 2为椭圆形横截面，No. 3 ~ No. 12为随机横截面。a为椭圆形横截面长轴的长度，b为短轴的长度。No. 1 is a circular cross-section, No. 2 is an elliptical cross-section, and No. 3−No. 12 are random cross-sections. a is the length of the major axis of the elliptical cross-section, and b is the length of the minor axis.
Figure 2. Cross-section shape of trunk models
![]()
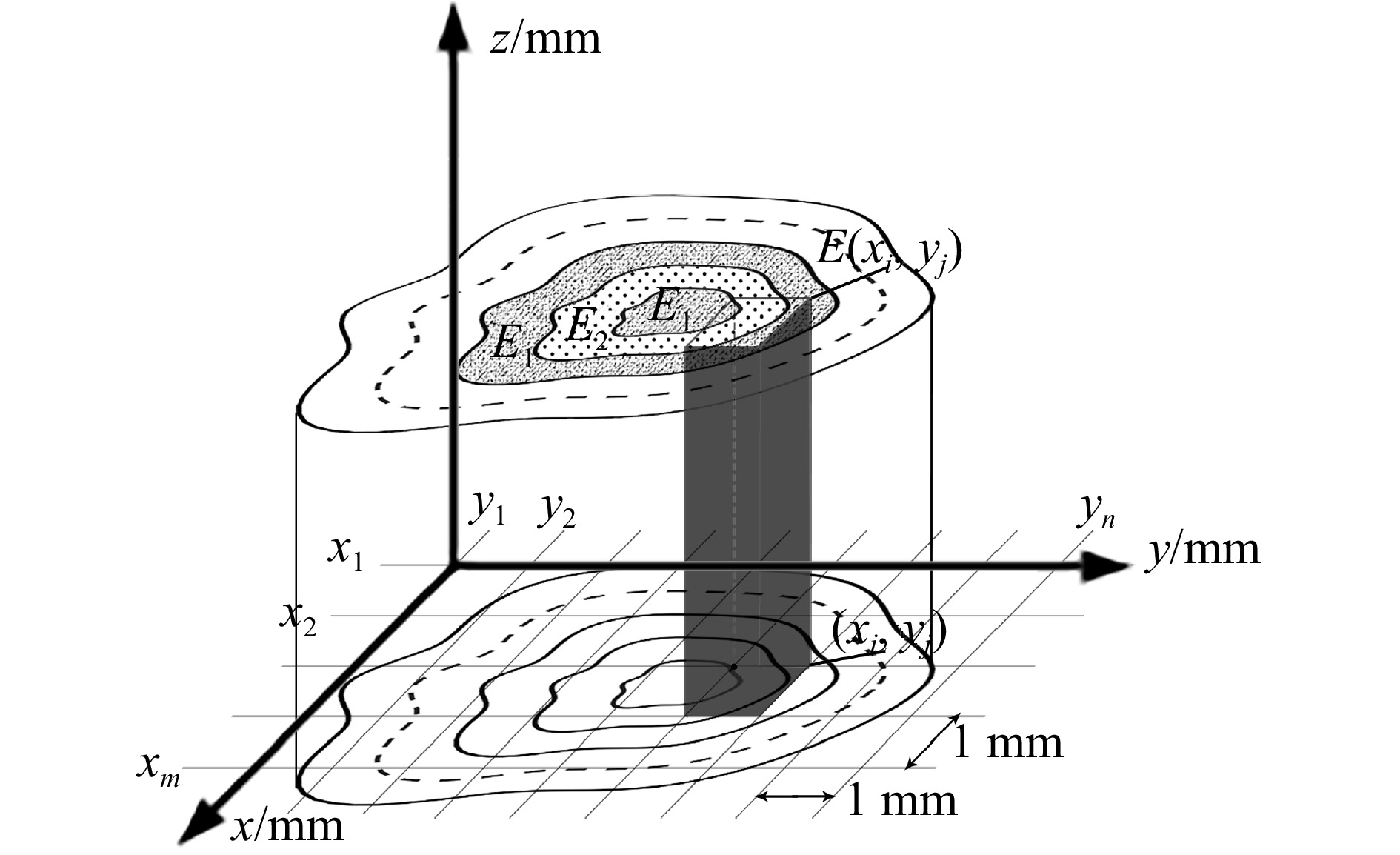
图 3 树干模型内部结构
O为坐标系原点，P为髓心（多层同心）或者圆心（圆形缺陷），OP的长度被定义为偏心距e，N为截面分层层数，E1为早材的弹性模量，E2为晚材的弹性模量，r为缺陷半径，E3为缺陷的弹性模量，E4为无缺陷树干的弹性模量，α为载荷方位角，β是所建模型的弯曲中性轴倾斜角，β0是均匀材质的弯曲中性轴倾斜角，γ为β到β0的偏转角。O is the origin of coordinate system, P is the centre of pith (multi-layer concentric) or the centre of circle (circular defect), the length of OP is defined as eccentricity distance e, N is number of delamination layers in cross-section, E1 is modulus of elasticity of earlywood, E2 is modulus of elasticity of latewood, r is radius of defect, E3 is modulus of elasticity of defect, and E4 is modulus of elasticity of non-defective trunk, α is azimuth of wind load, β is bending neutral axis tilt angle of constructed model, β0 is bending neutral axis tilt angle of homogeneous material, γ is relative deflection angle from β to β0.
Figure 3. Internal structure of trunk models
![]()
图 4 数值积分示意图
E1为早材的弹性模量，E2为晚材的弹性模量，E(xi,yj)为网格节点(xi,yj)上的弹性模量。E1 is modulus of elasticity of earlywood, E2 is modulus of elasticity of latewood, and E(xi,yj) is modulus of elasticity at grid joint (xi,yj).
Figure 4. Schematic diagram of numerical integration
![]()
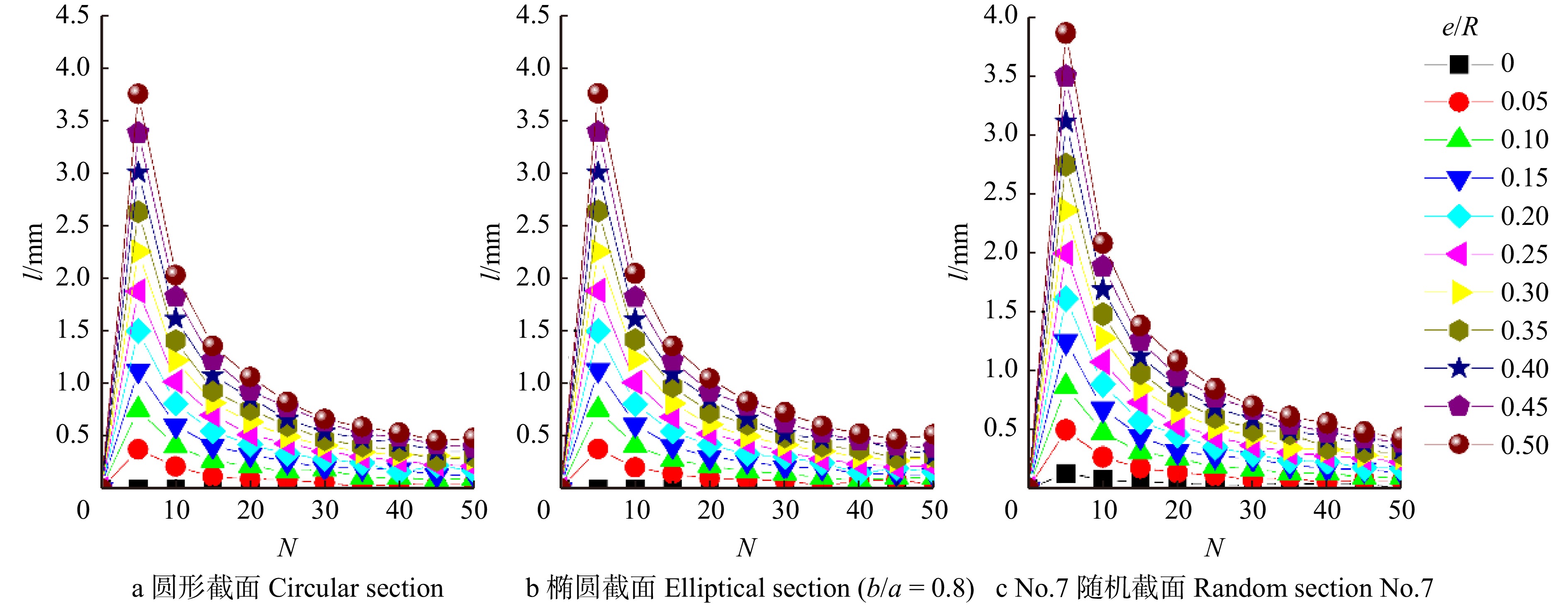
图 6 多层同心结构模型中 N对l的影响（E1/E2 = 0.5）
E1为早材的弹性模量，E2为晚材的弹性模量； e为偏心距，R为基圆半径；b/a为椭圆的短轴与长轴之比；N为截面分层层数；l为点O、C之间的距离（图1）。下同。E1 is modulus of elasticity of earlywood, E2 is modulus of elasticity of latewood. e is eccentricity distance, R is radius of base circle. b/a is ratio between the minor and major axis of ellipse, N is number of delamination layers in cross-section, l is distance between O and C (Fig. 1). The same below.
Figure 6. Effects of N on l in models of multi-layer concentric structures (E1/E2 = 0.5)
![]()
图 7 多层同心结构模型中E1/E2 对l的影响（N=50）
Figure 7. Effects of E1/E2 on l in models of multi-layer concentric structures (N=50)
![]()
图 8 多层同心结构模型中e/R对l的影响（E1/E2 = 0.5）
Figure 8. Effects of e/R on l in models of multi-layer concentric structures (E1/E2 = 0.5)
![]()
图 9 随机森林算法对多层同心结构模型中l的训练结果
Figure 9. Training results of l in multi-layer concentric structures by random forest algorithm
![]()
图 10 多层同心结构模型中l的分布
Figure 10. Distribution of l in multi-layer concentric structure models
![]()
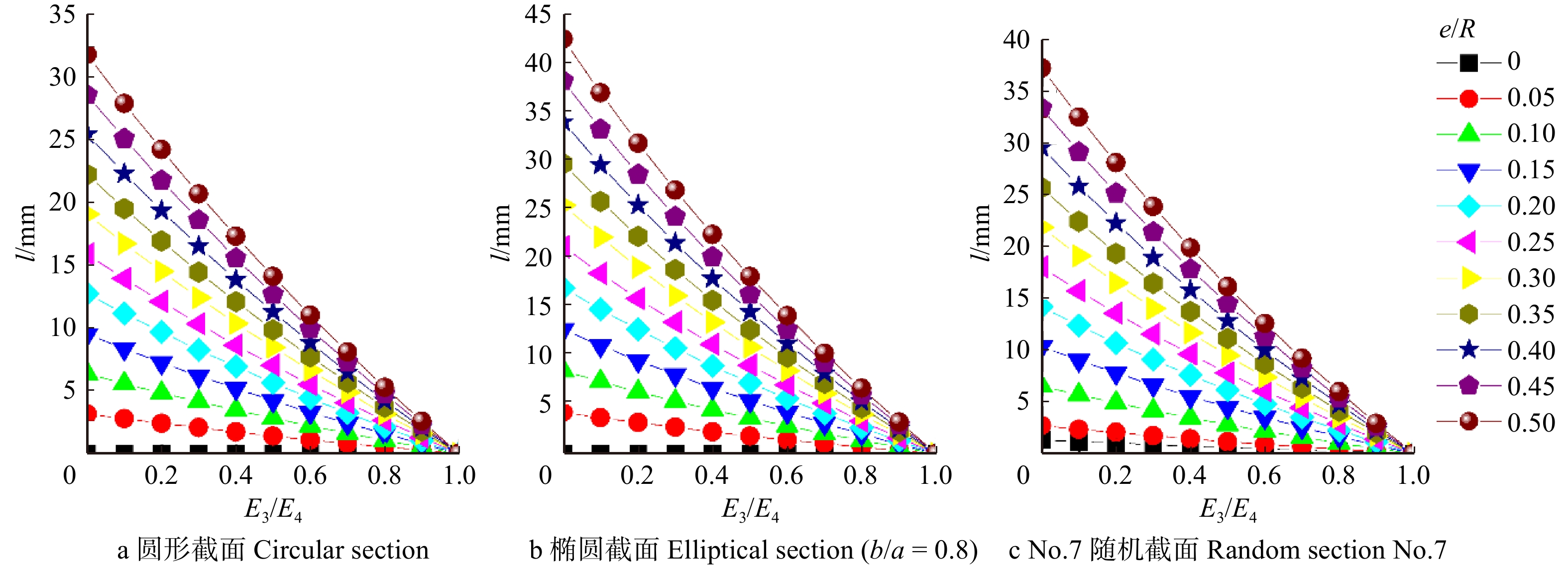
图 11 圆形缺陷模型中E3/E4对l的影响（r/R = 0.5）
r为缺陷半径，E3为缺陷树干的弹性模量，E4为无缺陷树干的弹性模量，下同。r is radius of defect, E3 is modulus of elasticity of defective trunk, E4 is modulus of elasticity of non-defective trunk, e is eccentricity distance, R is radius of base circle. The same below.
Figure 11. Effects of E3/E4 on l in circular defect models (r/R = 0.5)
![]()
图 12 圆形缺陷模型中r/R对l的影响（E3/E4 = 0.5）
Figure 12. Effects of r/R on l in circular defect models (E3/E4 = 0.5)
![]()
图 13 圆形缺陷模型中e/R对l的影响（E3/E4 = 0.5）
Figure 13. Effects of e/R on l in circular defect models (E3/E4 = 0.5)
![]()
图 14 随机森林算法对圆形缺陷模型中l的训练结果
Figure 14. Training results of l in circular defect models by random forest algorithm
![]()
图 16 随机森林算法对多层同心结构模型中β的训练结果
Figure 16. Training results of β in multi-layer concentric structures by random forest algorithm
![]()
图 17 多层同心结构模型中γ的分布
Figure 17. Distribution of γ in multi-layer concentric structure models
![]()
图 18 随机森林算法对圆形缺陷模型中β的训练结果
Figure 18. Training results of β in circular defect models by random forest algorithm
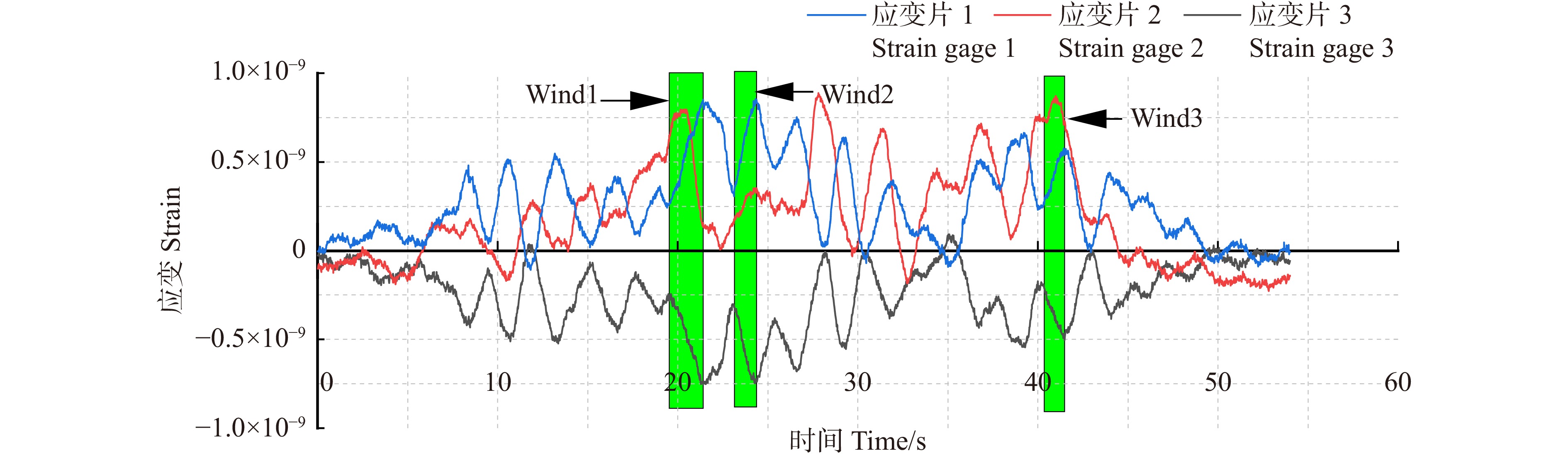
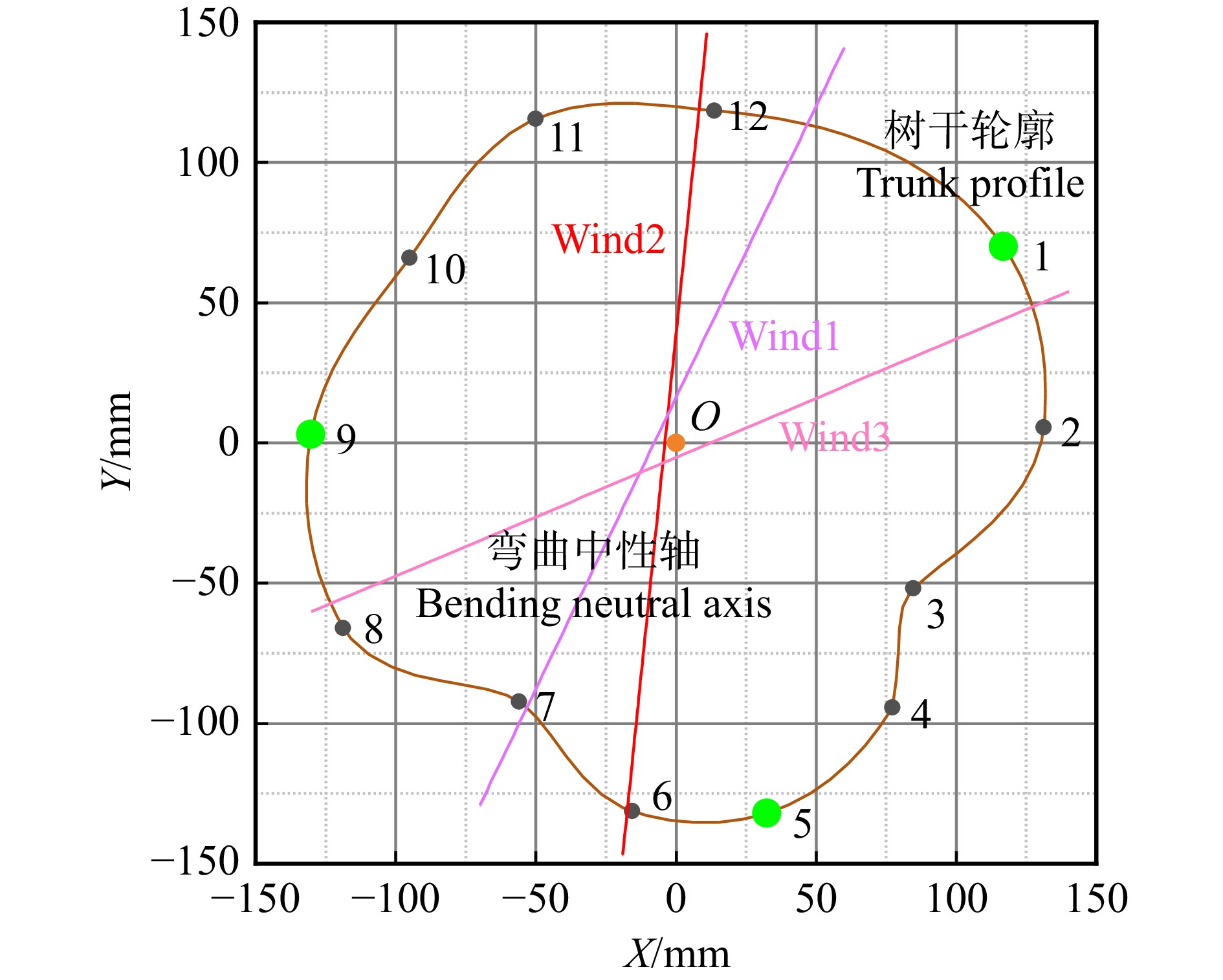
表 1 弯曲中性轴检测结果
Table 1 Bending neutral axis test results
风力区间
Wind zone斜率 Slope (k ) 截距 Intercept (b)/mm l/mm 平均值 Mean SD 平均值 Mean SD 平均值 Mean SD Wind1 2.077 5 16.957 4 16.242 0 27.952 8 13.289 9 6.710 4 Wind2 9.763 4 11.456 9 38.772 3 24.625 7 4.811 4 2.471 1 Wind3 0.422 9 0.304 4 −5.190 2 16.512 2 12.058 9 7.042 5 
下载: 导出CSV
-
[1] 陶嗣巍, 赵东. 树木几何结构快速建模的研究[J]. 北京林业大学学报, 2013, 35(2): 97−101. Tao S W, Zhao D. Rapid parametric modeling of geometry structure for trees[J]. Journal of Beijing Forestry University, 2013, 35(2): 97−101.
[2] Wu Y, Shao Z. Measurement and mechanical analysis of the strains–stresses induced by tree-pulling experiments in tree stems[J]. Trees, 2016, 30(3): 675−684. doi: 10.1007/s00468-015-1310-4
[3] 吴贻军, 姚剑飞, 吴俊, 等. 基于abaqus有限元法的空洞树干强度分析[J]. 西北林学院学报, 2022, 37(3): 205−210. doi: 10.3969/j.issn.1001-7461.2022.03.28 Wu Y J, Yao J F, Wu J, et al. Strength analysis of cavity tree trunks by finite element method based on abaqus[J]. Journal of Northwest Forestry University, 2022, 37(3): 205−210. doi: 10.3969/j.issn.1001-7461.2022.03.28
[4] 张鳌, 冀晓东, 丛旭, 等. 基于线性滤波法的单株林木抗风有限元模拟[J]. 北京林业大学学报, 2016, 38(2): 1−9. Zhang A, Ji X D, Cong X, et al. Finite element modeling of wind resistance of single trees based on linear filtering method[J]. Journal of Beijing Forestry University, 2016, 38(2): 1−9.
[5] 尤磊. 基于点云数据的树干干形测量[D]. 北京:中国林业科学研究院, 2016. You L. Stem form measurement based on point cloud data[D]. Beijing: Chinese Academy of Forestry, 2016.
[6] 李秀莲, 邵楠. 非对称截面梁的弯曲正应力分析[J]. 青海大学学报(自然科学版), 2010, 28(1): 67−72. Li X L, Shao N. The analysis on the bending normal stress of a non-symmetric section beam[J]. Journal of Qinghai University (Natural Science), 2010, 28(1): 67−72.
[7] 于永柱, 管成, 张厚江, 等. 古建筑墙体木柱缺陷对其安全性影响数值模拟研究[J]. 北京林业大学学报, 2022, 44(1): 132−145. doi: 10.12171/j.1000-1522.20210341 Yu Y Z, Guan C, Zhang H J, et al. Numerical simulation on the influence of wall wood column defects on the safety of ancient building[J]. Journal of Beijing Forestry University, 2022, 44(1): 132−145. doi: 10.12171/j.1000-1522.20210341
[8] 欧自娜, 张厚江, 管成. 古建筑七架梁缺陷安全性影响数值模拟研究[J]. 北京林业大学学报, 2020, 42(4): 142−154. doi: 10.12171/j.1000-1522.20190328 Ou Z N, Zhang H J, Guan C. Numerical simulation of the safety influence of defects on qijia-beams of ancient timber building[J]. Journal of Beijing Forestry University, 2020, 42(4): 142−154. doi: 10.12171/j.1000-1522.20190328
[9] 刘丰禄, 姜芳, 张建中, 等. 落叶松生材12个弹性常数的试验研究[J]. 西北林学院学报, 2015, 30(6): 227−231. doi: 10.3969/j.issn.1001-7461.2015.06.41 Liu F L, Jiang F, Zhang J Z, et al. Twelve elastic constant values of larch forest[J]. Journal of Northwest Forestry University, 2015, 30(6): 227−231. doi: 10.3969/j.issn.1001-7461.2015.06.41
[10] 王振刚. 含损伤梁结构的刚度及变形分析[D]. 西安: 西安理工大学, 2020. Wang Z G. Analysis of stiffness and deformation of beam structure with damage[D]. Xi’an: Xi’an University of Technology, 2020.
[11] 吴晓, 杨立军. 双模量泡沫铝芯夹层梁的弯曲计算分析[J]. 应用力学学报, 2015, 32(6): 922−927. Wu X, Yang L J. Bending calculation and analysis of bimodulous aluminum foam corelaminated beam[J]. Chinese Journal of Applied Mechanics, 2015, 32(6): 922−927.
[12] 姚文娟, 叶志明. 不同模量理论弹性支承连续梁及框架[J]. 力学与实践, 2004, 26(4): 37−41. doi: 10.3969/j.issn.1000-0879.2004.04.011 Yao W J, Ye Z M. The elastic supported continuous beam and frame of different modulus[J]. Mechanics in Engineering, 2004, 26(4): 37−41. doi: 10.3969/j.issn.1000-0879.2004.04.011
[13] Mattheck C. Wood: the internal optimization of trees[J]. Arboricultural Journal, 1995, 19(2): 97−110. doi: 10.1080/03071375.1995.9747051
[14] Krauss A, Moliński W, Kúdela J, et al. Differences in the mechanical properties of early and latewood within individual annual rings in dominant pine tree (Pinus sylvestris)[J]. Wood Res-Slovakia, 2011, 56(1): 1−12.
[15] 葛晓雯. 腐朽对杨树木材及活立木干基截面弯曲特性的影响[D]. 哈尔滨: 东北林业大学, 2017. Ge X W. Effects of decay on section bending properties of poplar wood and trunks of standing trees[D]. Harbin: Northeast Forestry University, 2017.
[16] 郭莹洁, 赵荣军, 钟永, 等. 基于早晚材的兴安落叶松成熟材力学模型——顺纹抗拉弹性模量[J]. 林业科学, 2014, 50(9): 118−123. Guo Y J, Zhao R J, Zhong Y, et al. Mechanical models of Larix gmelinii mature clear wood based on the properties of earlywood and latewood: longitudinal modulus of elastic[J]. Scientia Silvae Sinicae, 2014, 50(9): 118−123.
[17] 徐金梅. 祁连山青海云杉木材性质对气候变化的响应[D]. 北京: 中国林业科学研究院, 2012. Xu J M. Response of wood properties in tree rings of Picea crassifolia in Oiliang Mountains to climate change[D]. Beijing: Chinese Academy of Forestry, 2012.
[18] 余雁. 人工林杉木管胞的纵向力学性质及其主要影响因子研究[D]. 北京: 中国林业科学研究院, 2003. Yu Y. Longitudinal mechanical properties and its main influencing factors of tracheids of Chinese fir from plantation [D]. Beijing: Chinese Academy of Forestry, 2003.
计量
- 文章访问数: 299
- HTML全文浏览量: 23
- PDF下载量: 44
