森林规划研究旨在通过合理安排营林措施的时空分布从而实现森林资源的综合效益最大化。但长期以来，许多国家制定的经营方案仅强调森林的木材生产和经济效益，而忽略了森林所能提供的其他众多生态和社会效益。近些年来，公众对森林生态系统价值的认识已经发生了重大变化，更强调通过维护合理的森林景观格局以实现森林生态功能的充分发挥，如野生动物生境保护、水源涵养、生物多样性维护、娱乐消遣以及提供就业机会等。显然，这些新的目标和要求需要新的优化求解技术，特别是当森林经营方案中包含空间约束要求。

现阶段，森林规划问题的优化求解技术主要包括传统的数学优化(如线性规划)和启发式算法(如模拟退火算法)。由于森林规划问题属典型的组合优化技术，因此规划问题的解空间会随着规划问题规模的增加而呈现出典型的非线性增加趋势^[1]。如果假设某区域有n个小班，每个小班有2种经营措施(如皆伐和不采伐)，则该地区所有经营方案的组合共有2ⁿ种可能，呈明显指数型增长趋势。若进一步假设该区域仅有2个小班，而每个小班备选经营措施可以有k个，则所有经营方案的组合共有k²种可能，呈明显幂函数增长趋势。显然，随着规划问题规模(由小班和经营措施数量共同决定)的持续增加，求解这些问题所需的计算时间和存储空间也会急速增加，进而出现所谓的“组合爆炸”现象。同时，空间约束要求还会使决策变量间呈现典型的非线性、非凸性以及非连续性特征，因此这类规划问题已经严重超出了传统数学优化技术的处理能力，需要寻求更为有效的替代技术。

模拟退火算法(SA)作为一种邻域搜索技术，已广泛应用于一系列重要的林业规划问题中，如Öhman等^[2]以具有相同经营措施小班间的公共边界长度占总边界长度的比例为目标，研究了长期(40年)森林经营规划中营林措施的聚集分布问题；Crowe等^[3]则以面积邻接约束(area restriction model, ARM)、蓄积均衡收获和期末存量为主要约束条件，研究了森林的空间收获安排问题；Baskent等^[4]以常用森林景观格局指数、蓄积收获均衡和面积邻接约束为基础，建立了森林景观的空间优化模型；Öhman等^[5]以均衡收获和期末存量为主要约束条件，建立了森林中野生动物的生境保护模型；在我国相关研究中，仅陈伯望等^[6]以森林空间聚集为例研究了森林的空间收获安排问题；刘莉等^[7]采用森林模拟优化模型(FSOS)研究了长白山林区的森林多功能经营，该模型同样采样模拟退火作为优化算法，这些研究均表明模拟退火算法能够有效提供复杂森林规划问题的满意解(森林经营方案)。然而，这些研究均是基于标准的模拟退火算法实施的，即1-邻域技术。根据Bettinger等^[8]定义，如果每次优化过程中仅调整1个小班的经营措施，则可将其考虑为1-邻域(或1-opt)；但当同时调整λ个小班的经营措施时，则可将其理解为λ-邻域(或λ-opt)。在林业领域中，邻域搜索技术已经得到广泛应用，如Heinonen等^[9]研究表明SA算法2-邻域技术能够将森林空间收获安排问题的目标函数值平均提高约0.25%；Caro等^[10]指出2-邻域技术同样可提高禁忌搜索(tabu search)算法的求解效率，其中3种不同规模(即6400、14400和27000个小班)规划问题的目标函数值分别被提高了约3.32%、3.82%和12.75%，但近期Bachmatiuk等^[11]研究表明2-邻域技术仅能够显著提高相对简单规划问题的目标解质量，而当规划变得较为复杂时，该方法的求解效率则会显著降低。

综上所述，现阶段关于邻域搜索技术在森林空间规划问题中的求解效率还存在较大争议，同时鉴于森林空间规划以及启发式算法在我国当前的森林经营研究中还鲜有报道。因此，本研究以模拟退火算法为例，系统评估不同邻域搜索技术在森林空间规划问题中的应用潜力。研究中所涉及的森林规划问题均以50年规划周期(10个规划分期)内的最大化木材收获为目标函数，同时规划模型还需满足蓄积收获均衡约束、期末存量约束、单位限制模型和绿量约束等条件。为了定量评估不同算法的优劣程度及其对小班数量的响应，本研究采用3个模拟的栅格数据集，其分别包含了400、3600和10000个小班，最后采用配对T-检验分析不同邻域搜索技术目标函数值的差异显著性。

1.   材料与方法

1.1   研究数据

为了有效评估不同邻域搜索技术的求解效率及其对小班数量的响应，本研究设计了3种不同规模的栅格数据集，分别由20行×20列(林分Ⅰ，400个)、60行×60列(林分Ⅱ，3600个)、100行×100列(林分Ⅲ，10000个)的林分组成。每个栅格(小班)代表 10hm²的长白落叶松(Larix olgensis)人工林，每个小班的年龄采用随机数生成，均匀分布在0~50年之间，除此之外假设其他所有小班属性(如密度、立地等)均完全相同。3个林分的龄级分布频率如表 1所示。各小班单位面积木材收获量的预测采用戎建涛等^[12]建立的长白落叶松人工林蓄积公式，该公式仅以小班年龄作为自变量而不考虑其他因素(如立地、密度等)的影响。

表  1  模拟数据集的林分龄级结构分布

Table  1.  Number distribution of different age-classes for the three hypothetical forest datasets with 400, 3600 and 10000 units, respectively

林分 Forest	年龄范围Age class
	0~5	6~10	11~15	16~20	21~25	26~30	31~35	36~40	41~45	46~50
Ⅰ	43	38	44	42	29	40	43	35	41	45
Ⅱ	405	352	352	358	355	360	344	330	360	384
Ⅲ	1169	991	991	1000	992	990	1008	963	973	923

下载: 导出CSV 

| 显示表格

式中：V、t分别为小班蓄积和年龄；a、b、c分别为Richards方程的位置、尺度和形状参数，a=244.216，b=0.091，c=12.126。模型预估精度达92.077%。

需要说明的是，虽然这类林分数据集与现实中的林分数据结构和格局不完全相同，但其对我国平原地区人工商品林生产基地的经营管理仍具有重要借鉴意义，且这类数据在国外学者的森林经营规划研究中也得到广泛使用^[13-14]。在所有的森林采伐模拟中，本研究所考虑的经营措施仅包括2种，即皆伐与不采伐。此外，所有的决策变量均为0-1型变量，即不允许任何一个小班被多种经营措施分割，同时假设森林的所有采伐活动均在每个规划分期的期中进行。若某个小班被采伐后，将以相同树种立即进行更新造林，之后该小班蓄积仍采用经验模型来预估。为了避免对中幼龄林的过渡干扰，本研究中最小收获年龄约束均假设为31年，即当小班年龄小于该数值时，优化程序将不会产生相关决策变量。

1.2   森林空间收获

规划模型以50年规划期内最大收获蓄积为目标函数，而约束条件则主要涉及森林经营措施的空间和非空间约束。非空间约束由最小收获年龄、收获次数、蓄积均衡收获以及期末存量等约束组成，而空间约束则主要由邻接约束和绿量约束组成。因此，本文所建立的森林空间收获安排模型可归纳为：

满足

式中：T为规划分期数；N为研究区域内小班数量；i为任意小班；t为任意规划分期；m为第t规划分期的相邻分期，其中m∈{T_m}；z为小班i的任意邻接小班；N_i为小班i的所有相邻小班；A_i为小班i的面积；V_i为规划期初小班i的蓄积；V_it为小班i在第t分期收获时的蓄积；H为规划期初的总蓄积量；H_t为第t分期的总收获蓄积量；${{\hat V}_i}$为规划期末小班i的蓄积；${\hat H}$为规划期末林分的总蓄积量；α为规划分期t-1和t的总收获蓄积量的允许波动范围，本研究中假设为15%；β为规划期末小班总蓄积量较规划期初的增加比例，本研究限制为20%；X_it为0-1型变量，即如果小班i在第t分期被安排采伐，则X_it =1，否则，X_it =0；X_zm为0-1型变量，即如果小班z在第m分期被安排采伐，则X_zm =1，否则，X_zm =0；T_m为规划模型中相邻小班的绿量约束，可看作限制相邻小班被同时采伐的时间缓冲窗口；若某小班被安排在第t分期进行采伐，则其绿量约束范围(T_m)应满足：${T_m} \in \left\{ {{m_1} = t - 2, {m_2} = t - 1, {m_3} = t, {m_4} = t + 1, \left. {{m_5} = t + 2} \right\}} \right.$, 如果m_z＜0, 则T_m=0, 且如果m_z＞T, 则T_m=T；Age_it为小班i在第t分期的年龄；Age^min为政策允许(或用户设定)的最小收获年龄，设定为31年。

上述方程中，式(2)定义了该规划问题的目标函数，即最大化木材收获；式(3)~(5)分别用于计算规划期初林分总蓄积量(H)、各规划分期收获蓄积量(H_t)以及规划期末林分蓄积存量(${\hat H}$)；式(6)和式(7)要求相邻规划分期蓄积收获量波动应保持在一定范围内，本研究设定为15%；不等式(8)确保规划期末林分蓄积存量满足约束条件；式(9)表示森林经营措施的单位限制模型(unit restriction model，URM)，该约束严格禁止相邻小班(即具有共同边界的2个小班)在相同(或相近)规划分期内被同时采伐^[15]，同时该公式还考虑了2个规划分期的绿量约束，即相邻小班被禁止采伐的周期范围应包括在T_m内，显然这样有利于避免形成大面积、连续皆伐迹地，从而引起生境破碎、水土流失等问题；式(10)要求所有的森林采伐均需满足最小收获年龄的约束；式(11)要求每个小班在整个规划分期内被采伐次数至多不超过一次；式(12)要求所有的决策变量必须为0-1型，即每个小班不允许被多种经营措施(即皆伐和不采伐)分割。

1.3   模拟退火算法

根据式(9)~(11)的约束条件进行整理后，发现3个数据集分别涉及3293、29536和81625个0-1型决策变量，同时各规划问题还伴随着严格的收获均衡、期末蓄积存量以及空间邻接约束，这些限制明显超出了传统数学优化技术的求解能力。因此，本研究采用模拟退火算法对上述复杂的森林规划问题进行优化求解，并系统评估不同邻域搜索技术的优化求解效率。模拟退火算法是一种典型的邻域搜索技术，其核心是通过有条件地接受恶化解来提高算法获得最优解的概率，该特征有利于促使算法的搜索过程跳出局域收敛。因此，该算法不仅能够促使算法探索更多的解空间，同时也有利于增加算法获得最优解的概率。同其他启发式技术(如禁忌搜索、遗传算法等)一样，模拟退火算法并不能保证获得规划问题的最优解，但其优点是能够在有限的时间内提供一系列满意解。作为一种搜索过程，模拟退火算法已经被众多学者应用于森林管理规划问题^[2-8]。本研究选择模拟退火算法，一是因为该算法是林业中应用最为广泛的启发式技术，二是该算法已被其他学者证实可为各种森林规划问题提供足够优秀的目标解^[8]。本研究中，该算法初始解的生成始终采用蒙特卡洛模拟方法。

在第1种搜索策略中，本研究采用1-邻域技术来获得满意的目标解(即森林经营方案)。每次优化仅通过改变1个小班的经营措施或者收获分期来产生新解。对于任意一个可行解，其邻域可行解的产生可通过以下3种方式实现，即：1)如果小班i在当前解中未被安排采伐，则可将其在新解中设置在第t分期进行采伐；2)如果小班i在当前解中被安排在第t分期进行采伐，则在新解中将其设置在第p分期进行采伐(p≠t)；3)如果小班i在当前解中被安排在第t分期进行采伐，则在新解中设置该小班为不被采伐。当上述过程执行完成后，算法首先评价其是否满足相应的约束条件，即式(6)~(11)，如果满足所有约束，则该新解为可行解；否则，为不可行解。一直重复上述过程，直至获得可行解为止。

第2种搜索策略采用2-邻域技术，即通过同时、随机地改变2个小班的经营措施来产生新解，类似于Heinonen等^[9]和Caro等^[10]的研究策略。但该方法与Bettinger等^[7]采用的2-opt技术存在两个明显的区别，即：1)搜索过程中始终不使用1-邻域技术；2)新解的产生是通过随机改变的方式，而不采用交换的策略。在Bettinger等^[8]的研究中，搜索过程首先使用M次的1-邻域过程，然后再执行N次的2-opt过程，一直重复该交换过程直到搜索结束为止。因此，Bettinger等^[8]采用的搜索技术可以被看作是多样化与强化技术的综合行为，而Heinonen等^[9]、Caro等^[10]所采用的技术则属于典型的多样化策略。显然，后者在理论上能够产生更优的目标解。

模拟退火算法的参数主要由初始温度、最终温度、冷却速率以及每温度下的交互次数等组成，用户可以通过调整各参数的取值来影响算法的优化过程。因此，用户必须针对不同的规划问题慎重选择相应参数的取值。为此，本研究采用Bettinger等^[8]提供的试错法(trial-and-error)来确定该规划问题的最优参数组合。经过一系列参数模拟后，最终确定的最优参数组合分别为：初始温度=10⁶, 最终温度=10, 冷却速率=0.99和每温度下重复次数=100，该参数集对应的迭代次数为114600次，即每次优化模拟可产生约11.46万个可行经营方案。此外，为了消除模拟退火算法随机因素的影响，本研究对各优化算法随机模拟1000次，以其统计值(如平均值、标准差等)作为评估各算法性能的主要依据。同时，采用方差分析(ANOVA)评估不同算法在求解森林规划问题中的差异显著性。根据上述模拟退火算法的基本原理和规划问题，采用面向对象思想在Microsoft Visual Basic 6.0平台上编程实现，同时为了确保各搜索策略的优化时间具有可比性，所有模拟均在安装有Windows 7旗舰版32位操作系统的个人电脑(2.6GHz Core i5处理器)上进行，整个优化过程共持续了约500h(2种方法×3个数据×1000次模拟×5min/次)，即21d左右。

2.   结果与分析

当采用2-邻域搜索技术时，各规划问题最小和最大目标函数值平均提高约0.62%和1.95%，相当于每公顷林地可多采0.82和3.03m³木材；而对各规划问题平均目标函数值而言，3个林分呈现完全不同的变化趋势，其中林分Ⅰ平均目标函数值略有增加(0.17%)，林分Ⅱ平均目标函数值略有减小(-0.26%)，而林分Ⅲ平均目标函数值则显著减小(-2.87%)；各规划问题目标函数值变异系数显著减小约11.44%，说明这些规划问题目标函数值的聚集度显著增加。T-检验表明，除林分Ⅲ以外，模拟退火算法2种搜索技术所获得的目标函数值均无显著差异(表 2)。综上所述，模拟退火算法邻域搜索技术求解效率可能与规划问题规模及其复杂程度有关，但该结论仍需进一步验证。

表  2  模拟退火算法不同邻域搜索技术目标函数值统计特征

Table  2.  Statistical characteristics of objective function values for different neighborhood search techniques of simulated annealing

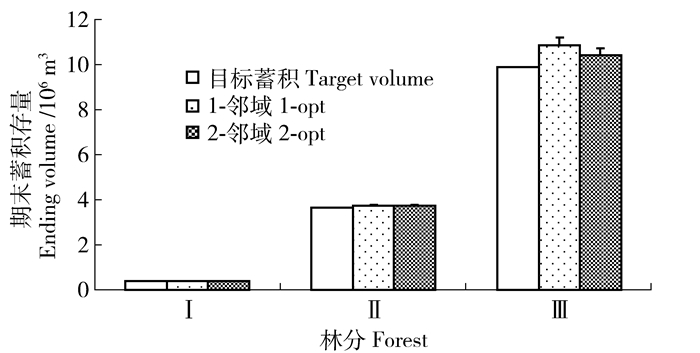
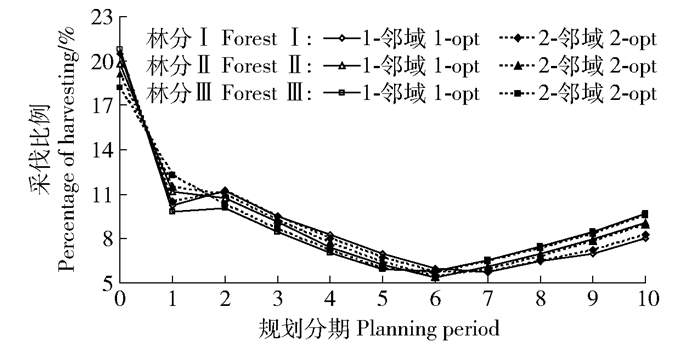
林分 Forest	方法 Method	收获蓄积Harvest volume						T-检验T-test
		最小值Min./106m3	最大值Max./106m3	平均值Mean/106m3	标准差Std/106m3	变异系数CV/%		T值T-value	P值P-value
Ⅰ	1-opt	0.5532	0.6222	0.5675	0.0134	2.3565		-1.73	0.08
	2-opt	0.5559	0.6373	0.5685	0.0126	2.2209
Ⅱ	1-opt	4.7410	5.6831	4.9103	0.2178	4.4357		1.03	0.30
	2-opt	4.7657	5.7269	4.8974	0.1799	3.6739
Ⅲ	1-opt	12.7823	15.4751	13.9459	1.0100	7.2420		6.55	0.00
	2-opt	12.8926	15.8850	13.5555	0.8699	6.4174

下载: 导出CSV 

| 显示表格

图 1显示，无论采用哪种邻域搜索技术，各林分不同分期收获蓄积均存在一定波动，即整体随着规划分期呈先减小后增加趋势，但其均满足均衡收获约束(式(5)~(6)和图 1)。当采用1-邻域搜索技术时，3个规划问题最优解各分期平均蓄积收获量分别为0.06×10⁶m³、0.57×10⁶m³和1.55×10⁶m³，变异系数分别约为20.54%、22.34%和19.52%；而当采用2-邻域搜索技术时，最优解各分期平均蓄积收获量分别增加了约2.43%、0.77%和2.65%，变异系数也分别增加了约7.14%、0.15%和17.94%。鉴于本文规划模型以整个规划周期内最大化木材收获量为目标函数(式(2))，因此模拟结果仅能保证各规划问题中2-邻域最大目标函数值优于1-邻域，而不能保证2-邻域获得的最优森林经营方案中各分期的木材收获量同样大于1-邻域。根据式(7)可知，各林分规划期末蓄积存量应满足一定约束限制，即期末蓄积存量至少应维持在0.41×10⁶m³、3.62×10⁶m³和9.78×10⁶m³以上，而优化结果显示各林分规划期末蓄积存量分别比预期目标增加了约0.17%、1.90%和7.67%(图 2)，说明规划结果符合期末蓄积存量约束。图 3给出了模拟退火算法不同邻域搜索技术所获得的各规划问题中最优解对应的各分期采伐小班数量占总小班数的百分比，可以看出不同搜索技术、不同大小规划问题(即小班总数量)所获得的各分期采伐小班数量比例均无显著差异，但整体呈现出先减小后增加的趋势。各种规划情景均在第1分期采伐小班数量最多，平均约为19.82%，而在第6分期采伐数量最少，平均仅为5.67%，显然这种趋势是与各分期安排的收获蓄积量相对应的。以林分Ⅰ为例，图 4给出了2种邻域搜索所获得的最优森林经营方案时空分布，可以看出虽然不同邻域搜索最优解中各林分采伐分期不完全一致，但各分期所采伐的小班数量总量及其比例差异不显著。

图  1  模拟退火算法不同邻域搜索最优解各分期收获蓄积

Figure  1.  `Harvest volume of each period of the optimal solutions for the three hypothetical forest datasets when employed with 1-opt and 2-opt moves

下载: 全尺寸图片 幻灯片

图  2  模拟退火算法不同邻域搜索最优解期末蓄积存量

目标蓄积即为式(8)期末蓄积存量约束，其计算公式可表示为：H(1+β)，其中H为规划期初整个林分的总蓄积量，β为期末总蓄积较期初的增加比例，此处设定为20%，因此各林分目标蓄积分别为0.41×10⁶、3.62×10⁶和9.78×10⁶m³。

Figure  2.  Mean amount of the ending inventory volume for the optimal solutions when employed with 1-opt and 2-opt moves

Target volume is formula (8): ending volume constraint, its calculating formula is showed as H(1+β), in which H means the total volume of forest at the initial stage of planning, β means the increased percentage at the end of stage compared with the initial stage, here set it as 20%. So the target volume for each stand is 0.41×10⁶, 3.62×10⁶ and 9.78×10⁶m³, respectively.

下载: 全尺寸图片 幻灯片

图  3  模拟退火算法不同邻域搜索最优解采伐小班的数量比例

Figure  3.  Percentages of harvesting units for each period of the optimal solution when employed using 1-opt and 2-opt moves

下载: 全尺寸图片 幻灯片

图  4  模拟退火算法不同邻域搜索最优森林采伐方案的时空分布(林分Ⅰ)

图中灰色表示采伐；白色表示不采伐。

Figure  4.  Temporal and spatial distributions of optimal solution for forestⅠwhen employed 1-opt and 2-opt moves, respectively

The gray color indicates that the management unit is assigned to be harvested in that period, and the white color indicates that the management unit is not assigned to be harvest.

下载: 全尺寸图片 幻灯片

算法优化时间是评价启发式算法性能的另一个重要指标。图 5给出了各规划问题每次优化模拟过程中算法首次获得最大目标函数值所需的时间，可以看出各规划问题优化时间均存在较大变异，其中当采用1-邻域搜索技术时，3个林分所需平均时间分别为35.12、86.27和380.84s，变异系数分别高达68.56%、190.50%和89.60%；而当采用2-邻域搜索技术时，各林分所需平均时间分别为76.14、166.43和271.25s，其变异系数也分别达到42.66%、269.97%和120.22%。此外，对于林分Ⅰ和林分Ⅱ而言，2-邻域搜索技术首次达到最大目标函数值所需的时间大约是1-邻域搜索技术的2倍左右(具体值是2.17和1.93倍)；但对林分Ⅲ而言，2-邻域所需时间却显著减少，仅为1-邻域的0.71倍左右。

图  5  模拟退火算法不同邻域搜索策略的平均优化时间

Figure  5.  Mean optimization time of different neighborhood search techniques of simulated annealing algorithm

下载: 全尺寸图片 幻灯片

3.   结论与讨论

森林经营措施时空分布特征对森林生态系统的潜在影响正受到越来越多的重视，但当考虑森林经营措施的空间关系时，规划模型无疑会变得极为复杂而难以有效求解，即表现为随着规划模型复杂程度的增加，算法陷入局域最优的概率也会随之增加，同时算法获得的目标解也可能远离规划问题的全局最优解。因此，寻求积极有效的优化求解技术已经成为当前森林规划研究领域的热点和难点。邻域搜索的核心思想是通过对算法优化过程中的当前解不断进行“微调”进而实现增加算法跳出局域最优解和增加算法获得全局最优解概率的一种优化策略。作为一种替代策略，2-opt技术已被部分学者证实可应用于一系列的复杂森林规划问题，但近期Bachmatiuk等^[11]以模拟退火算法为例开展的相关研究表明2-邻域技术仅适用于复杂程度相对较低的规划问题。因此，现阶段不同学者对2-邻域优化策略的效果还存在较大争议，同时鉴于森林空间规划以及启发式算法在我国当前的森林经营研究中还鲜有报道。为此，本研究以模拟退火算法为例，系统评估不同邻域搜索技术在森林空间规划问题中的应用潜力。

在有关森林经营规划中不同算法性能的比较研究中，虽然各算法机理(如新解产生、接受机制)对其搜索性能起决定性作用，但其仍受不同学者所涉及的规划问题、模拟数据以及算法实施环境和技巧的影响。Heinonen等^[9]采用效用函数理论将均衡蓄积收获、期末蓄积存量和森林经营措施空间分布共3个子目标整合到目标函数中，而不涉及任何形式的约束条件，因此他们的模型在理论上不存在非可行解的情况，这与本研究所建立的规划模型存在显著不同。本研究模拟结果表明：3个林分的最大目标函数值均呈显著增加趋势，同时目标函数值间的变异系数显著减小；但随着小班数量的不断增加，各规划问题的平均目标函数值则呈现出复杂的变化趋势，其中林分Ⅰ的平均目标函数值略有增加(0.17%)，而林分Ⅱ和林分Ⅲ的平均目标函数值则呈明显下降趋势(0.26%和2.80%)。因此，可认为2-邻域技术的搜索效率与规划问题的规模显著有关，这与Bachmatiuk等^[11]的研究结果基本一致。而对于Caro等^[10]的研究，虽然其规划模型也涉及了复杂的收获均衡约束、邻接约束、绿量约束以及生境质量约束等，但其采用的禁忌搜索算法与模拟退火算法在搜索机理上却完全不同。概括来说，模拟退火算法采用概率接受机制来避免陷入局部最优，而禁忌搜索则采用禁忌周期来避免算法陷入局部最优^[16]。因此，关于2-邻域搜索策略在其他启发式算法中的应用仍有待进一步研究。此外，现阶段已有多种启发式算法被广泛应用于林业规划问题中，如蒙特卡洛模拟、禁忌搜索、遗传算法、门槛接受算法等。这些算法在基本原理、新解产生和接受机制等方面均存在显著差异，因此针对林业规划问题系统评估各算法的搜索性能及其应用环境同样值得深入研究。

为了评估不同小班(或决策变量)数量对邻域搜索技术在森林规划问题中应用效果的影响，本研究设计了3种不同规模的栅格数据集。在该类数据集中，每个小班均有相同且稳定的空间邻接关系(边界小班除外)，即该小班的上(n-N)、下(n+N)、左(n-1)、右(n+1)各一个邻接小班，其中n为小班从左到右、从上到下的编号且不包括边界小班，N为林分的列数，这显然与真实的林分空间关系不一致，如董灵波^[17]指出大兴安岭盘古林场(6421个小班)每个小班的相邻小班数量高达5.46±1.90个。但采用该类数据结构可有效忽略复杂林分空间关系对算法比较结果的潜在影响，从而有利于实施一个精确的控制实验，例如采用T-检验、方差分析等比较不同算法目标函数值的差异显著性。因此，这类数据已经在算法比较研究中得到广泛使用^{[8, 13-14]}，但针对真实林分数据的比较研究仍具有重要意义。

需要强调的是，当前我国已经进入全面停止天然林的商业性采伐阶段，因此可选森林经营措施(如择伐、皆伐等)正受到越来越多的限制。根据我国当前森林经营政策的约束，抚育将成为我国(特别是东北地区)今后森林经营的重要途径，但现阶段还缺乏科学合理的定量抚育技术以及能够精确反映不同抚育方式和强度对林分生长过程的预测模型，因此现阶段将抚育措施作为一种决策变量加入到规划模型中还面临着较大困难。为此，本研究对具体的森林经营过程进行了适当简化，即仅以皆伐措施为决策变量建立了适用于人工商品林生产基地的森林空间收获安排模型。因此，待上述技术发展成熟后，可逐渐开展基于抚育措施的森林经营规划研究。