基于Possion回归混合效应模型的长白落叶松一级枝数量模拟

王曼霖; 董利虎; 李凤日

doi:10.13332/j.1000-1522.20170204

基于Possion回归混合效应模型的长白落叶松一级枝数量模拟

东北林业大学林学院

基金项目:

“十三五”国家重点研发计划课题 2017YFD0600402

详细信息

作者简介:
王曼霖。主要研究方向：林分生长与收获模型。Email: 445947011@qq.com 地址: 150040 黑龙江省哈尔滨市和兴路26号东北林业大学林学院

责任作者:
李凤日，教授，博士生导师。主要研究方向：林分生长与收获模型。Email: fengrili@126.com 地址:同上

中图分类号: S758.5
计量
- 文章访问数: 3611
- HTML全文浏览量: 647
- PDF下载量: 74
出版历程
- 收稿日期: 2017-06-11
- 修回日期: 2017-10-18
- 发布日期: 2017-10-31

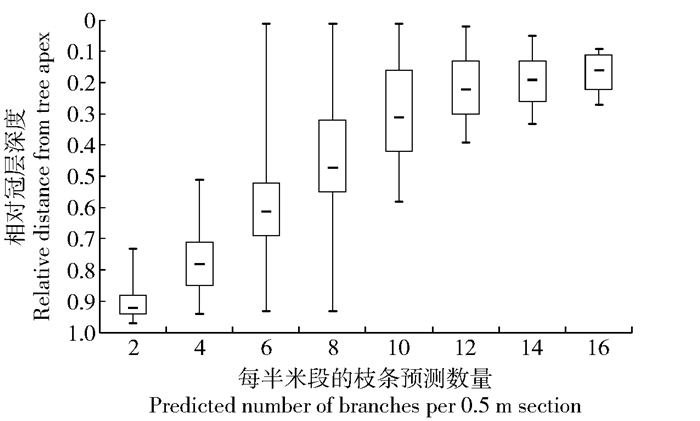
First-order branch number simulation for Larix olgensis plantation through Poisson regression mixed effect model

School of Forestry, Northeast Forestry University, Harbin, Heilongjiang, 150040, P. R. China

摘要

摘要: 利用广义线性混合模型对长白落叶松一级枝条数量进行研究，以黑龙江省佳木斯市孟家岗林场长白落叶松人工林为研究对象，基于7块标准地49株枝解析样木的596个一级枝条测定数据，利用SAS 9.3软件中的PROC GLIMMIX模块，建立了基于Poisson分布的一级枝条数量的最优基础模型。在此基础上考虑树木效应，构建每半米段一级枝条数量的广义线性混合模型，并利用AIC、BIC、-2log likelihood以及LRT检验对收敛模型的拟合优度进行比较。结果表明：任意参数组合的混合效应模型的拟合效果均好于传统模型，最终将含有DINC、LnRDINC、RDINC²这3个随机效应参数的模型作为长白落叶松每半米段一级枝条数量分布的最优混合效应模型。模型拟合结果显示，LnRDINC、CL的参数估计值为正值，DINC、RDINC²、HT/DBH、DBH的参数估计值为负值，每半米段一级枝条分布数量在树冠范围内存在峰值，模型的确定系数R²为0.669，拟合的平均绝对误差为2.250，均方根误差为3.012。从总体上看，所建立的一级枝条分布数量混合模型不但可以反映总体枝条数量的变化趋势，还可以反映树木之间的个体差异，说明广义线性混合模型确实可以提高模型的模拟精度。所得出的混合模型可以很好地预估该研究区内人工长白落叶松每半米段一级枝条数量的分布情况，为定量研究长白落叶松树冠构筑型和三维可视化模拟提供了基础。
- 长白落叶松人工林 /
- 一级枝条数量 /
- Poisson回归 /
- 广义线性混合模型
Abstract: In this study, the generalized linear mixed model was used to study the distribution of number of first-order branch for planted Larix olgensis trees. The modeling data were based on 596 first-order branches of 49 branch analysis trees selected from 7 permanent sample plots in Larix olgensis plantation from Mengjiagang Forest Farm, Jiamusi City, Heilongjiang Province of northeastern China. Poisson model was introduced to develop the optimal basic model with the PROC GLIMMIX procedure of SAS. Considering the different tree effects, the generalized linear mixed model of number of first-order branch per 0.5 m was developed on the selected optimal basic model. AIC, BIC, -2log likelihood and LRT test were selected to compare the goodness-of-fit statistics of the models. The results showed that all of the convergence mixed models with the combination of random coefficients fitted better than the basic model. Finally, the one with three random coefficients (including DINC, LnRDINC, RDINC²) was selected as the optimal mixed model to describe the distribution of number of first-order branch per 0.5 m for planted Larix olgensis trees. In this model, the parameter values for LnRDINC and CL were positive; the ones for DINC, RDINC², HT/DBH, DBH were negative. Moreover, there was a peak value for the number of first-order branch per 0.5 m. The fitting result of model showed that the coefficient of determination (R²) was 0.669 and the mean absolute error was 2.250 and the root mean square error was 3.012. All in all, not only could the mixed model describe the mean trend of the branch distribution, but also it reflected the differences among sample trees. It was shown that the generalized linear mixed model could improve the simulation accuracy of the model. As a result, the optimal mixed model would be suitable for predicting the first-order branch quantity and will provide theoretic basis to modeling crown architecture and three-dimension visualization for Larix olgensis plantation.
- Larix olgensis plantation /
- first-order branch distribution /
- Poisson regression model /
- generalized linear mixed model

HTML全文

在农林业生产中，植物常遭受重金属等各种土壤条件胁迫。铅(Pb)是重金属污染物中影响较严重的元素之一，又是植物非必需元素，其在组织中大量积累会引起植物体内细胞膜脂过氧化，最终影响生长和品质^[1-2]，因此修复Pb胁迫土壤具有重要意义。作为生态修复的重要内容之一，植物修复已成为近年来国际环境领域研究的热点^[3]。在Pb胁迫土壤的植物修复中，特别是在植物生长初期，如何提高植物适应性和存活力尤其引人关注。

作为一种天然螯合剂，土壤中各种来源的有机酸显著影响重金属在土壤中的迁移转化行为及植物有效性，在控制Pb等重金属生物毒性方面发挥重要作用^[4-5]。植物对重金属的解毒机制包括外部排斥和内部耐受两类，这两类机制中有机酸均起重要作用^[6-7]。外部排斥机制即有机酸与金属离子形成稳定的金属配位体复合物，阻止金属离子进入植物体内或避免其在根部敏感位点累积；内部耐受机制即有机酸可与进入植物体内的金属离子螯合，使其转化为无毒或毒性较小的结合形态^[7-8]。在重金属胁迫下，植物一般通过多种机制的联合以防止中毒，但植物种类不同解毒机制也不同^[7]。有机酸还显著影响Pb胁迫下植物的多种生理生化特性、生长和生物量分配格局，最终提高Pb胁迫土壤上植物的生态适应性及土壤修复效率^[4]。有机酸对上述指标的影响，不仅与植物种类有关，还与有机酸种类和浓度、Pb胁迫程度和处理时间等密切相关^[11]。目前，有机酸提高植物适应性的作用已在一些植物上证实，如欧洲油菜(Brassica napus)、马蔺(Iris lactea var. chinensis)等，有机酸种类涉及草酸、柠檬酸和水杨酸等，测定指标涉及电导率、可溶性蛋白含量、Pb吸收和生物量积累等^[9-11]。值得指出的是，除上述常规指标外，叶绿素荧光参数、根系形态特性和养分元素吸收也是鉴定植物抗逆性的重要指标，是植物适应土壤环境的基础^[12]；且F₀、F_v/F_m和F_v/F₀等荧光指标、比根长等根系形态特征及Fe等养分元素吸收状况对Pb胁迫都非常敏感^[13-14]。但目前，外源有机酸影响植物对土壤Pb胁迫的适应性研究仍集中在农业领域，在林业领域相对较少，特别是如何影响Pb胁迫下林木的叶绿素荧光参数、根系形态特性和营养元素吸收运输还鲜见报道。

我国东北林区有一定面积的矿山土急需复垦，如黑龙江省伊春西林铅锌矿等。这些立地条件下，Pb胁迫普遍存在。长白落叶松(Larix olgensis)是东北山区的重要乡土树种，因成活率高和对环境要求不甚严格，就成为Pb胁迫矿山土植被恢复和林业复垦的先锋树种。但在较严重的Pb胁迫下，其成活和生长仍受较大限制，特别是初期“造林不成活”现象普遍存在。通过前人研究可以假设，外源有机酸亦能在苗期提高长白落叶松对Pb胁迫的适应性和抗性。但目前，有机酸如何影响Pb胁迫下长白落叶松幼苗的生态适应性还未见报道。草酸和柠檬酸是我国东北林区森林凋落物淋洗液中存在的2种优势有机酸，数量均较为可观^[15]。本文模拟此区长白落叶松凋落物淋洗液中草酸和柠檬酸浓度范围^[15]，通过外源添加不同浓度草酸或柠檬酸溶液，系统研究了不同处理时间下，有机酸对长白落叶松幼苗多种生理生化特性、Pb及养分元素吸收及生长的影响，特别是首次揭示了有机酸如何影响Pb胁迫下苗木的叶绿素荧光参数、根系形态特征及养分元素吸收状况。研究旨在探讨有机酸对Pb胁迫下苗木生态适应性的调控意义及机制，从而为有机酸应用于Pb矿区废弃地的植被恢复提供生理生态学理论依据，也能为Pb胁迫土壤的有效利用开辟新思路。

1. 材料与方法

1.1 苗木培育与处理

实验在东北林业大学帽儿山实验林场温室内进行。长白落叶松种子选种、消毒、雪藏催芽后，2016年4月末播种于塑料育苗盆(底径16.2 cm、上口径18.4 cm、高20.0 cm)，覆土料为质地均一、无杂质的A₁层暗棕壤(本区地带性土壤，基本性质见表 1)。土壤采自林场内长白落叶松人工林下，去除根系、土壤动物等，自然风干1 d，装盆，每盆5.5 kg。每盆育苗60株，盆上沿土壤空出2~3 cm以浇水、有机酸和Pb处理。2016年5月末间苗，每盆剩30株(由于当地气候条件限制，苗木生长缓慢，出苗1个月时平均苗高仅4.3 cm，平均地径1.05 cm，这样的密度有利于形成良好的种群优势，而不会产生生长空间的竞争)。

表 1 供试A₁层暗棕壤的基本性质

Table 1. Selected properties of A₁ horizon of dark brown forest soil used in the experiment

土壤层次 Soil layer	pH值 pH value (H₂O)	阳离子交换量 Cation exchange capacity/(cmol·kg^-1)	有机质 Organic matter/ (g·kg^-1)	全氮 Total N/ (g·kg^-1)	全磷 Total P/ (g·kg^-1)	速效磷 Available P/ (mg·kg^-1)	土壤质地 Soil texture	黏粒Clay (<2 μm)/ (g·kg^-1)	草酸含量 Oxalic acid concentration/(μg·kg^-1)	柠檬酸含量 Citric acid concentration/(μg·kg^-1)
A₁	5.32	40.2	107.9	6.39	2.08	45.8	壤质 Loamy texture	135	310.98	139.83
注：30 mmol/L NH₄F+25 mmol/L HCl浸提法；A₁为暗棕壤层。下同。Notes: means extracted with 30 mmol/L NH₄F+25 mmol/L HCl; A₁ means horizon of dark brown forest soil. The same below.

下载: 导出CSV

| 显示表格

缓苗1月后，将Pb(NO₃)₂溶液均匀地添加到土壤中以进行Pb胁迫处理，使土壤内Pb²⁺含量达100 mg/kg(依前期调查的黑龙江省伊春西林铅锌矿区土壤Pb含量设定)。Pb处理10 d后，采取灌根方式进行外源有机酸添加处理[草酸(OA)或柠檬酸(CA)]，使土壤内有机酸浓度分别达0、0.04、0.2、1.0和2.0 mmol/kg。另外，在长白落叶松苗期，由于其根系生长慢且发育不完全^[16]，还采用类似叶面施肥的方式进行了有机酸喷施^[17]。具体讲：将有机酸溶液(浓度分别为0、0.2、1.0、5.0和10.0 mmol/L)均匀地喷施在苗木叶片的上、下表面，以叶面均匀湿润为止。实验处理见表 2。有机酸以有机盐形式添加(pH 5.16，仿当地土壤溶液平均pH值)，每天1次，共7 d，均在早晨08:00进行。土壤无Pb胁迫、等量蒸馏水处理为对照(CK)。由于当地气候寒冷，温室育苗最早也得在4月末进行，8月下旬叶片已开始变黄脱落，不能再进行相关指标的准确测定。综合考虑出苗、缓苗、Pb胁迫和有机酸处理等时间，分别在有机酸处理后第10、20、30天采样分析。每处理栽10盆苗，每个处理时间10个重复，3个时间共300盆。

表 2 实验设计(10、20、30 d均进行如下处理)

Table 2. Experimental layout (each of the treatments below was sampled after 10, 20, or 30 days)

处理Treatment	土壤处理Soil treatment	有机酸类型Kind of organic acid	有机酸浓度Concentration of organic acid/(mmol·L^-1)
CK	A₁、无Pb A₁, no Pb	―	0
T1	A₁+Pb	―	0
T2	A₁+Pb	OA	0.2
T3	A₁+Pb	OA	1.0
T4	A₁+Pb	OA	5.0
T5	A₁+Pb	OA	10.0
T6	A₁+Pb	CA	0.2
T7	A₁+Pb	CA	1.0
T8	A₁+Pb	CA	5.0
T9	A₁+Pb	CA	10.0

下载: 导出CSV

| 显示表格

1.2 样品采集与测定

1.2.1 生理生化指标和元素含量

在各处理10盆苗木中，随机采集中部叶片(约2.0 g)，立即、分别用上海雷磁DDS-6700电导仪和考马斯亮蓝G-250染色法测定相对电导率和可溶性蛋白含量。再随机采集苗木中部叶片，把采过叶片的幼苗小心地从土中取出(避免根系损伤)，采集 < 2 mm细根。叶片和细根用蒸馏水洗净擦干，105 ℃下杀青15 min，70 ℃下烘至恒质量，粉碎，过2 mm尼龙筛，用微波消解ICP-MS法测定叶片和细根Pb、Mg和Fe含量。每处理重复3次。

每处理选3株幼苗暗处理20 min后，选取完整叶片用LI-6400 XT便携式光合仪(Licor，US)测定叶绿素荧光指标。通过测得的F₀(初始荧光)和F_m(最大荧光)，计算得到F_v/F_m和F_v/F₀，其中F_v=F_m-F₀。每处理重复3次。

1.2.2 根系形态特征

在各处理10盆苗木中，每处理随机选3株幼苗，小心地将根系取出，用去离子水洗净，用滤纸小心吸干，用枝剪将根、茎和叶分开，再用根系分析仪(Win-RHI Z0-2004a，Canada)测定根系形态，得到表面积、长度、体积和平均直径，并计算得到比根长(长度/干质量)。

1.2.3 生长

在各处理10盆苗木中，每处理选15株幼苗，小心地从盆中取出，将茎、叶和根分开，用去离子水洗净吸干，105 ℃下杀青15 min，60 ℃下烘至恒质量，得到各部分干质量及平均值。

1.3 数据处理

用SPSS 18.0对数据进行统计分析，采用Duncan新复极差法对所有指标数据进行差异显著性检验(P < 0.05)。

2. 结果与分析

2.1 苗木细胞膜透性变化

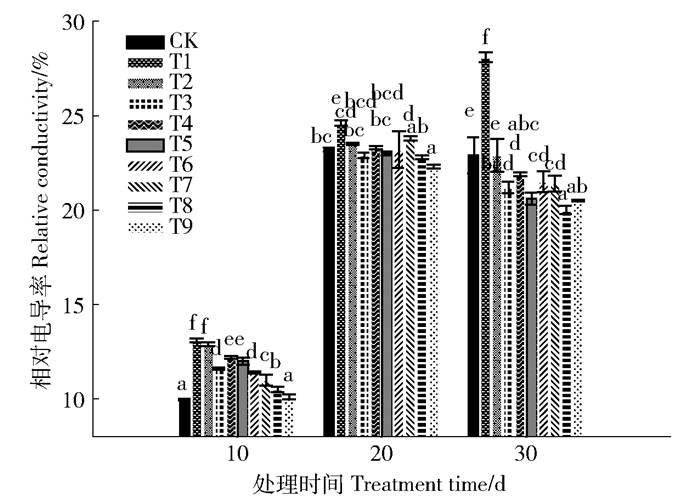
与对照(CK)比，Pb胁迫(T1)增加苗木叶片相对电导率，说明叶片细胞膜受损，且时间越长损伤越重。与无有机酸处理(T1)相比，草酸和柠檬酸显著降低Pb胁迫下苗木的相对电导率，2种有机酸均在10.0 mmol/L效果最好，柠檬酸强于草酸，不同时间效果为30 d>10 d>20 d(图 1)。

图 1 有机酸处理后长白落叶松叶片的相对电导率

不同字母表示差异显著(P < 0.05)。

Figure 1. Relative conductivity of Larix olgensis leaves with different organic acids

Bars labeled with different letters are significantly different (P < 0.05).

下载: 全尺寸图片幻灯片

2.2 可溶性蛋白含量变化

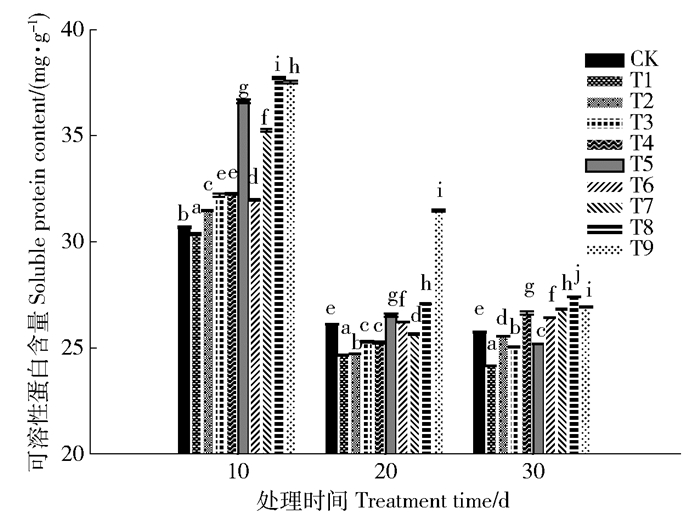
与CK相比，苗木叶片可溶性蛋白含量在Pb胁迫后(T1)降低(时间越长降幅越大)，但有机酸处理后显著提高，所有处理均达显著水平，5.0或10.0 mmol/L效果最好，2种有机酸增幅均为10 d>30 d>20 d，柠檬酸作用强于草酸(图 2)。

图 2 有机酸处理后长白落叶松叶片的可溶性蛋白含量

Figure 2. Soluble protein contents of Larix olgensis leaves with different organic acid treatments

下载: 全尺寸图片幻灯片

2.3 叶片叶绿素荧光参数变化

Pb胁迫显著影响叶片叶绿素荧光指标，F₀升高，F_m、F_v、F_v/F_m和F_v/F₀均降低。有机酸使上述指标均向相反方向变化，变化幅度与其浓度大体呈正相关，一般10.0 mmol/L变幅最大。不同时间内各指标变幅不同：F₀为30 d>20 d>10 d，F_m为30 d>10 d>20 d，F_v为30 d>20 d>10 d，F_v/F_m和F_v/F₀为30 d>20 d>10 d。除少数0.2 mmol/L处理外，柠檬酸影响均强于草酸(图 3)。

图 3 有机酸处理后长白落叶松叶片的叶绿素荧光参数

Figure 3. Chlorophyll fluorescence parameters of Larix olgensis leaves induced by different organic acids

下载: 全尺寸图片幻灯片

2.4 根系形态特征变化

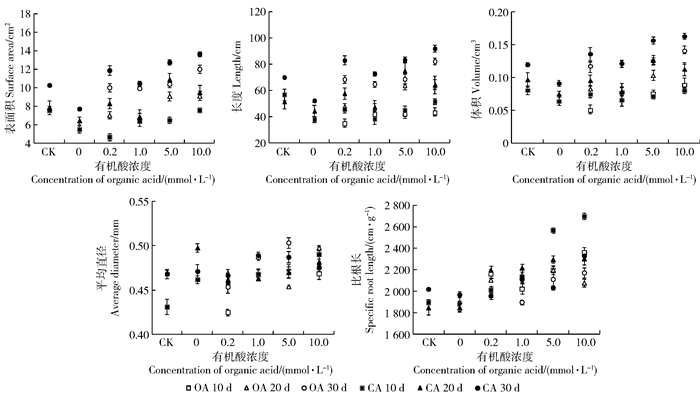
Pb胁迫显著影响苗木根系形态特征，表面积、长度、体积和比根长降低，时间越长降幅越大，但平均直径增加。有机酸使上述指标向相反方向变化，大都以10.0 mmol/L影响最显著，柠檬酸强于草酸。表面积、长度、体积、比根长和平均直径时间序列分别为30 d>20 d>10 d，30 d>20 d>10 d，30 d>20 d>10 d，10 d>20 d>30 d和10 d>30 d>20 d(图 4)。

图 4 有机酸处理后长白落叶松幼苗的根系形态特征

Figure 4. Root morphological parameters of Larix olgensis seedlings induced by different organic acids

下载: 全尺寸图片幻灯片

2.5 苗木体内Pb和营养元素含量变化

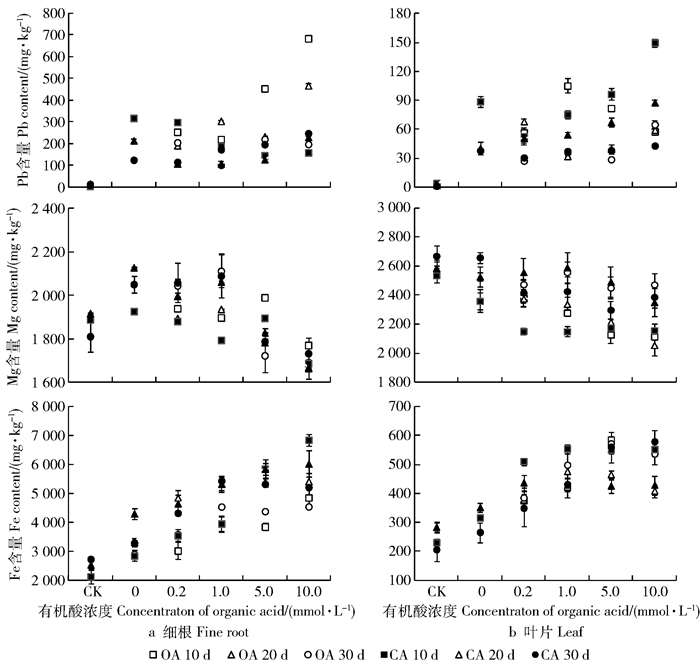
Pb胁迫显著增加细根和叶片Pb含量，且在根部强烈积累。有机酸使细根和叶片Pb含量先降后增，大多在10.0 mmol/L时仍低于有机酸0组(T1)。对于根系Pb积累，草酸影响大多强于柠檬酸，叶片则相反。不同有机酸浓度和处理时间内无明显规律。Pb胁迫增加细根和叶片Fe含量及细根Mg含量，但降低叶片Mg含量。有机酸降低细根和叶片Mg含量，但增加Fe含量，大多在10.0 mmol/L变幅最大。不同时间内细根Mg含量降幅为30 d>20 d>10 d，Fe含量增幅为10 d>20 d>30 d；叶片Mg含量降幅为30 d>20 d>10 d，Fe含量增幅为30 d>10 d>20 d。除极少数处理外，柠檬酸效果强于草酸(图 5)。

图 5 有机酸处理后长白落叶松细根和叶片Pb及营养元素含量

Figure 5. Pb and nutrient contents in fine roots and leaves of Larix olgensis seedlings with organic acid treatments

下载: 全尺寸图片幻灯片

2.6 生长变化

与CK相比，Pb胁迫显著降低苗木的根、茎和叶干质量，但有机酸处理后各部分干重量大多显著增加，一般10.0或5.0 mmol/L增加效果最显著，不同时间的增加效果为20 d>30 d>10 d，柠檬酸效果强于同浓度草酸(图 6)。

图 6 有机酸处理后长白落叶松的根、茎和叶干质量

△ OA叶OA leaf ▲ CA叶CA leaf ○ OA茎OA stem ● CA茎CA stem □ OA根OA root ■ CA根CA root

Figure 6. Dry mass of root, stem and leaf of Larix olgensis seedlings with organic acid treatments

下载: 全尺寸图片幻灯片

3. 讨论

3.1 有机酸对Pb胁迫下细胞膜系统的保护作用

Pb胁迫显著增加长白落叶松叶片相对电导率和质膜透性(图 1)，可能Pb与细胞膜上的磷脂作用形成正磷酸盐、焦磷酸盐，从而改变膜结构；或者Pb被细胞壁上果胶酸吸附，改变了细胞壁弹性和塑性，损害了壁的生理功能^[18]。本结果与玉米(Zea mays)^[18]、海榄雌(Avicennia marina)^[19]等研究一致。Pb胁迫下，草酸和柠檬酸显著降低长白落叶松相对电导率(图 1)，说明有机酸减缓了电解质渗出和细胞膜损伤，能通过提高质膜系统稳定性诱导苗木适应性，此结果与柠檬酸和草酸对马蔺^[9]、柠檬酸对灯心草(Juncus effuses)^[20]等研究一致。

3.2 有机酸与Pb胁迫下的渗透调节物质

作为渗透调节物质，可溶性蛋白含量能反映植物总体代谢状况及抗逆性^[21]。Pb降低长白落叶松叶片可溶性蛋白含量(图 2)，说明此时苗木体内代谢改变及蛋白质合成受阻，且时间延长影响增大。Pb胁迫下蜡熟期玉米、镉(Cd)污染下苎麻(Plagiomnium acutum)等研究也如此，且随重金属浓度升高而下降^{[18, 22]}。但也有人认为，Pb等胁迫下，植物除合成蛋白质以络合进入体内的重金属离子、降低其危害外，可溶性蛋白含量上升还能增加细胞渗透浓度和功能蛋白数量，有助于维持细胞正常代谢^[23]。

外源有机酸提高长白落叶松可溶性蛋白含量(图 2)，说明此时苗木的生理生化反应与代谢活动都显著增强，进而能从渗透调节角度提高苗木对Pb胁迫的适应性。同样，1.5和4 mmol/L柠檬酸也使苎麻叶片和根系可溶性蛋白含量分别增加2.9和6.4 mg/g，但高浓度草酸(9 mmol/L)却使叶片含量降低3.1 mg/g^[22]。

3.3 叶绿素荧光对Pb胁迫和有机酸的响应

Pb诱导长白落叶松叶片F₀显著上升(图 3)，这与Pb、Cd胁迫下银芽柳(Salix leucopithecia)、云南樟(Cinnamomum glanduliferum)等研究一致^[24-25]，且增加越多损伤越重^[26]。但Pb降低黑麦草(Lolium perenne)F₀，随其浓度而下降，可能因为Pb降低叶绿素含量，使捕获和传递给PSII反应中心的光能减少、电子传递受阻^[27]。Pb还降低长白落叶松F_v/F_m和F_v/F₀(图 3)，说明Pb离子抑制光合作用原初反应，使其开放程度和捕获激发能效率下降，这可能与其抑制叶绿素合成有关，或由于Pb竞争性抑制放氧复合体中23kd蛋白上Ca²⁺和Cl^-结合位点，从而阻止电子从PSII向PSI传递^[28]。本结果与云南樟^[25]、尖叶走灯藓(Plagiomnium cuspidatum)^[29]、玉米^[30]、黑麦草^[31]等研究一致。但也有不同报道，如100 μmol/L和0.25 mmol/L Pb分别对柳条莫丝(Fontinalis antipyretica)和玉米F_v/F_m影响均不明显^{[28, 32]}。Pb引起F_v/F_m和F_v/F₀变化一般与其浓度显著正相关^{[28, 33]}，且有明显的时间效应，时间越长长白落叶松F_v/F_m和F_v/F₀降幅越大(图 3)，但高浓度Pb使湿地匍灯藓(Plagiomnium acutum)F_v/F₀第1天即明显降低，低浓度则先增后降^[34]。

有机酸如何影响植物(特别是重金属胁迫下)叶绿素荧光参数目前还鲜见报道。Pb等重金属可能通过影响水裂解端电子流而降低PSII原初光能捕获能力和电子传输能力^[35]，抑制点主要在光系统II氧化面^[36]。Pb还刺激PSII核心蛋白磷酸化，影响PSII复合物稳定性和D₁蛋白降解速率^[30]。Pb和柠檬酸存在下，田青(Sesbania drummondii)幼苗F_v/F_m和F_v/F₀不变，光合效率正常^[37]；但Pb和草酸或柠檬酸处理下，长白落叶松F₀降低，F_v/F_m和F_v/F₀升高(图 3)，说明有机酸明显抑制Pb引起的PSII光合反应中心损伤，有效缓解反应中心吸收的光能用于电子传递量子产额的降幅，减轻光合电子传递和光抑制，提高了光合活性。上述差异可能与植物类型、Pb处理方式和水平及有机酸浓度等不同有关。

3.4 Pb胁迫、有机酸与植物根系形态、元素吸收和生长

Pb降低长白落叶松根系表面积、长度、体积和比根长(图 4)，说明Pb已超过苗木耐受范围，并抑制根系纵向生长，这与高羊茅(Festuca elata)、多年生黑麦草^[38]、马蔺^[10]及麻疯树(Jatropha curcas)^[39]等研究一致。Pb还增加苗木根系平均直径(图 4)，即使根系变粗膨大，可能因为Pb影响了根细胞增殖和分化，特别是根尖细胞的分裂分化。Pb对根系毒害明显强于芽等其他器官^[40-41]，可能因为根最先感受毒害，根细胞壁上还有能大量固定Pb离子的交换位点，根尖吸收Pb后诱发过量的自由基产生，从而伤害根系代谢中的琥珀酸脱氢酶等，降低根系活力，并抑制其向地上部转移^[42]。

有机酸明显促进Pb胁迫下长白落叶松生长(图 6)，可能原因包括：1)有机酸益于叶绿素荧光、可溶性蛋白等生理特性(图 1~3)，这不但能提高光合速率促进有机物积累，还有益于水和无机盐运输。2)有机酸促进根系生长(图 4)，这能缓解Pb对根系活力和生理功能的限制，还增加苗木与土壤的接触面积及Fe等养分的吸收利用(图 5)，减缓Pb胁迫导致的某些养分吸收利用受抑而引起的干物质积累减少。Pb也破坏菲白竹(Pleioblastus fortunei)体内矿质营养平衡，特别是打破Na⁺/K⁺平衡是Pb毒害主要原因^[43]。本结果与柠檬酸、草酸等对马蔺影响一致^[9]。对长白落叶松生理特性和养分吸收的影响柠檬酸均强于草酸，对生长影响也如此。

外源有机酸能缓解植物的重金属中毒症状，在植物对重金属的外部排斥(即避性机制)和内部耐受等机制中均发挥重要作用^{[7-8, 44]}如柠檬酸和酒石酸分别可减轻Pb、Cd对萝卜(Raphanus sativus)的毒害^[45]，柠檬酸还促进Pb和Cd从其根系向地上部的转运^[46]。本研究发现，较低浓度草酸和柠檬酸处理时，长白落叶松幼苗细根和叶片Pb含量降低，说明此时苗木对Pb胁迫的解毒机制主要体现在外部排斥机制。5.0~10.0 mmol/L较高浓度有机酸处理时，苗木体内Pb含量升高，则此时内部耐受机制发挥的作用更大，但也不排除2种机制同时起作用的可能性。

4. 结论

1) 长白落叶松幼苗对Pb胁迫响应明显，叶片细胞膜透性和F₀提高，叶片可溶性蛋白含量、F_m、F_v、F_v/F_m和F_v/F₀，根系表面积、长度、体积和比根长都降低，细根和叶片Pb含量显著增加，叶片Mg含量及根、茎和叶干质量降低，且时间越长影响越大。

2) 外源草酸和柠檬酸使上述生理生化和根系形态指标均向相反方向变化，显著增加苗木各部分干质量，因此外源有机酸对提高长白落叶松对Pb胁迫土壤的生态适应性有积极意义。

3) 较低浓度草酸和柠檬酸对苗木解毒Pb胁迫的机制主要体现在外部排斥机制，5.0~10.0 mmol/L较高浓度处理时则内部耐受机制作用更大，但也不排除2种机制同时起作用的可能性。

4) 外源有机酸对苗木生态适应性的影响，一般在20或30 d、5.0或10.0 mmol/L效果最好，且柠檬酸强于草酸。

图 1 人工长白落叶松每半米段一级枝条数量分布

高径比、冠长模拟值来自胸径为13.5 cm的人工长白落叶松解析木。Simulated values of HT/DBH，CL based on a Larix olgensis with DBH=13.5 cm.

Figure 1. Predicted value of number of first-order branches per 0.5 m

下载: 全尺寸图片幻灯片

图 2 人工长白落叶松一级枝条数量的实测值与预测值散点图

Figure 2. Observed values and predicted values of first-order branch for Larix olgensis planation

下载: 全尺寸图片幻灯片

图 3 人工长白落叶松相对冠层深度与每半米段的预测枝条数量关系

Figure 3. Relationship between relative distance from tree apex and the number of predicted branches per 0.5 m section for Larix olgensis planation

下载: 全尺寸图片幻灯片

表 1 长白落叶松人工林林分因子统计表

Table 1 Statistics of stand variables for Larix olgensis planation

项目 Item	年龄/a Age/year	平均胸径 Mean DBH/cm	平均树高 Mean tree height/m	平均冠幅 Mean crown width/m	林分密度/(株·hm^－2) Stand density/(tree·ha^－1)	坡度 Slope/(°)	海拔 Altitude/m
最小值Minimum	9	5.40	6.20	1.10	1 016.70	5.00	141.80
最大值Maximum	33	19.90	24.10	1.60	3 083.30	12.50	260.10
平均值Mean	19.19	11.30	13.31	1.27	2 223.80	6.30	193.11
标准差Std	7.53	4.19	5.20	0.19	579.72	2.90	35.35
变异系数CV/%	39.24	37.08	39.07	14.96	26.07	46.03	18.31

下载: 导出CSV

表 2 长白落叶松人工林解析木和枝条分布统计表

Table 2 Statistics of sample trees and branch distribution for Larix olgensis planation

	项目 Item	胸径 DBH/cm	树高 Tree height (HT)/cm	冠长 Crown length (CL)/m	冠幅 Crown width (CW)/m	高径比 HT/DBH	每半米段的一级枝个数 Number of first-order branch per 0.5 m
建模数据(样本数量=40) Fitting data(sample size=40)	最小值Minimum	2.00	3.80	2.30	0.55	0.66	1
	最大值Maximum	27.00	21.50	11.50	3.18	1.41	26
	平均值Mean	13.68	12.45	6.24	1.42	0.85	7.56
	标准差Std	5.42	4.45	2.38	0.56	0.26	4.21
	变异系数CV/%	39.61	35.74	38.14	39.44	30.59	55.69
检验数据(样本数量=9) Validation data(sample size=9)	最小值Minimum	3.80	5.30	2.52	0.51	0.70	1
	最大值Maximum	25.20	21.30	10.51	3.20	1.39	23
	平均值Mean	14.03	12.86	6.01	1.49	0.81	7.83
	标准差Std	5.88	4.13	2.49	0.59	0.22	3.86
	变异系数CV/%	37.56	32.12	41.43	39.60	27.16	49.30

下载: 导出CSV

表 3 长白落叶松一级枝条数量模型所需变量及相关描述

Table 3 Symbol and associated description for variables tested in the first-order branch model for Larix olgensis planation

变量符号 Variable symbol	变量描述 Description
DINC	冠层深度Distance from tree apex
RDINC	相对冠层深度Relative distance from tree apex
LnDINC	冠层深度的对数值Logarithm of distance from tree apex
LnRDINC	相对冠层深度的对数值Logarithm of relative distance from tree apex
RDINC²	相对冠层深度的平方Relative distance from tree apex squared
DBH	树木胸高处的直径Diameter at breast height/cm
HT	树高Tree height/m
HT/DBH	树高和胸径的比值Ratio of tree height to diameter at breast height
CL	树冠冠长Crown length/m

下载: 导出CSV

表 4 基于树木效应的混合模型拟合结果

Table 4 Fitting results of mixed model based on individual tree effects

参数个数 Parameter number	模型 Model	随机参数Random parameter							AIC	BIC	-2log likelihood
参数个数 Parameter number	模型 Model	截距Intercept	HT/DBH	DINC	LnRDINC	CL	RDINC²	DBH	AIC	BIC	-2log likelihood
7	(7)	无None	2 610.85	2 640.17	2 596.85
	(8)	★							2 600.01	2 617.92	2 580.11
	(9)		★						2 599.16	2 619.67	2 582.16
	(10)			★					2 584.90	2 598.41	2 568.90
8	(11)				★				2 600.07	2 618.98	2 581.47
	(12)					★			2 600.19	2 616.50	2 582.99
	(13)						★		2 580.35	2 593.86	2 564.35
	(14)							★	2 599.50	2 616.01	2 586.50
10	(15)	★		★					2 575.01	2 591.90	2 555.01
	(16)	★			★				2 571.42	2 588.31	2 551.42
	(17)	★					★		2 574.70	2 591.98	2 554.70
	(18)		★	★					2 575.65	2 590.85	2 557.65
	(19)		★		★				2 576.51	2 593.40	2 556.61
	(20)		★				★		2 576.65	2 593.54	2 556.65
	(21)			★	★				2 572.97	2 589.86	2 552.97
	(22)			★		★			2 574.16	2 591.05	2 554.16
	(23)			★			★		2 568.91	2 585.80	2 548.91
	(24)			★				★	2 573.76	2 590.65	2 553.76
	(25)				★	★			2 573.08	2 589.97	2 553.08
	(26)					★		★	2 574.18	2 591.06	2 554.18
	(27)				★			★	2 583.32	2 600.20	2 563.32
	(28)					★	★		2 574.62	2 591.51	2 554.62
	(29)					★		★	2 580.54	2 592.43	2 561.54
	(30)						★	★	2 572.95	2 589.84	2 552.95
13	25(31)	★		★	★				2 568.95	2 590.91	2 542.95
	26(32)	★			★		★		2 566.07	2 588.03	2 540.07
	27(33)		★		★		★		2 570.77	2 592.73	2 544.77
	28(34)			★	★	★			2 568.37	2 590.32	2 542.37
	29(35)			★	★		★		2 565.65	2 587.61	2 539.65
	30(36)			★	★			★	2 572.20	2 594.15	2 546.20
	31(37)			★		★	★		2 569.04	2 590.99	2 543.04
	32(38)			★			★	★	2 567.45	2 589.40	2 541.45
	33(39)				★	★	★		2 565.74	2 587.70	2 539.74
	34(40)				★		★	★	2 568.37	2 590.32	2 542.37
注：参数个数包括固定效应参数个数、随机效应方差-协方差参数个数；带★变量表示包含此随机参数；表中的模型(7)即正文中的公式(7)，即不含随机效应参数的最优基础模型。Notes: the number of parameters includes the fixed parameters, parameters in covariance-structure G for random effect; variables with ★ are included in the random parameters; model (7) in the table is the formula (7) model, which is the optimal basic model without random effect parameters.

下载: 导出CSV

表 5 不同参数个数的模型固定参数和方差组成的估计值

Table 5 Fixed parameters and variance component estimates of models with different numbers of parameters

固定参数 Fixed parameter	模型(7) Model (7)	模型(13) Model (13)	模型(23) Model (23)	模型(35) Model (35)
截距Int	3.058 2	2.941 7	3.178 4	3.086 6
DINC	-0.002 1	-0.002 1	-0.002 2	-0.002 5
LnRDINC	0.342 3	0.361 7	0.370 9	0.415 3
RDINC²	-1.044 4	-1.153 0	-1.129 3	-1.046 1
HT/DBH	-0.282 2	-0.147 1	-0.280 3	-0.245 4
DBH	-0.015 3	-0.004 34	-0.007 4	-0.011 2
CL	0.094 9	0.080 4	0.076 7	0.105 0
随机效应方差-协方差结构 Variance of random effect-covariance structure		[0.279 1]	$\left[ {\begin{array}{*{20}{c}} {0.000\;01}&{ - 0.000\;99}\\ { - 0.000\;99}&{1.446\;3} \end{array}} \right]$	$\left[ {\begin{array}{*{20}{c}} {0.000\;001}&{0.000\;033}&{ - 0.001\;16}\\ {0.000\;033}&{0.004\;852}&{ - 0.011\;22}\\ { - 0.001\;16}&{ - 0.011\;22}&{1.565\;0} \end{array}} \right]$
LRT		32.5	15.44	9.26
P		<0.001	<0.001	0.026
Pearson χ²/自由度	1.73	1.50	1.38	1.20
Pearson χ²/degree	1.73	1.50	1.38	1.20

下载: 导出CSV

表 6 基于随机参数不同方差-协方差结构的混合模型模拟结果比较

Table 6 Comparisons of mixed model based on different variance-covariance structure of random parameters

方差-协方差结构 Variance-covariance structure	参数个数 Parameter number	AIC	BIC	-2log likelihood	LRT	P
复合对称矩阵Composite symmetric matrix (CS)	9	2 586.71	2 601.91	2 579.71
对角矩阵Diagonal matrix (UN(1))	13	2 580.99	2 597.87	2 560.99	18.72	< 0.001
无结构矩阵Non-structural matrix (UN)	13	2 565.65	2 587.61	2 539.65	21.34	—

下载: 导出CSV

表 7 检验数据的随机参数估计结果

Table 7 Random parameter estimation result of validation data

检验数据 Validation data	随机参数 Random parameter
检验数据 Validation data	DINC	LnRDINC	RDINC²
b₁	-0.000 5	-0.013 2	0.383 1
b₂	0.000 6	-0.022 6	-0.971 2
b₃	0.000 9	0.014 7	-1.068 5
b₄	0.000 8	-0.073 4	-1.525 0
b₅	0.000 1	-0.109 2	-1.883 0
b₆	0.000 7	0.044 0	-0.629 0
b₇	-0.001 6	-0.114 4	1.453 0
b₈	-0.001 6	-0.173 4	1.109 1
b₉	0.001 4	0.120 6	-1.083 0

下载: 导出CSV

表 8 基础模型和混合效应模型模拟结果比较

Table 8 Comparison of based model and mixed-effect model

评价指标 Evaluation index	固定模型 Fixed model	混合模型 Mixed model
确定系数 Determination coefficient (R²)	0.510	0.669
均方根误差 Root mean square error (RMSE)	3.396	3.012
平均绝对误差 Average absolute error (MAE)	2.601	2.250

下载: 导出CSV

参考文献(30)

[1]	BROWN P L, DOLEY D, KEENAN R J. Stem and crown dimensions as predictors of thinning responses in a crowded tropical rainforest plantation of Flindersia brayleyana F. Muell[J]. Forest Ecology & Management, 2004, 196(2/3): 379-392. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a09870ffce90b9fdf1ec2a36d7723f87
[2]	CRECENTE-CAMPO F, MARSHALL P, LEMAY V, et al. A crown profile model for Pinus radiata D. Don. in northwestern Spain[J]. Forest Ecology & Management, 2009, 257(12): 2370-2379. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=12965a1d48a157ea8ca6be89351acf79
[3]	KADANE J B, KRISHNAN R, SHMUELI G. A data disclosure policy for count data based on the Com-Poisson distribution[J]. Management Science, 2006, 52(10): 1610-1617. doi: 10.1287/mnsc.1060.0562
[4]	ZHANG H, XU J, JIANG N, et al. PLNseq: a multivariate Poisson lognormal distribution for high-throughput matched RNA-sequencing read count data[J]. Statistics in Medicine, 2015, 34(9): 1577-1589. doi: 10.1002/sim.6449
[5]	CHOOWOSOBA H, LEVY S M, DATTA S. Marginal regression models for clustered count data based on zero-inflated Conway-Maxwell-Poisson distribution with applications[J]. Biometrics, 2015, 72(2): 606-618. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cc718cf3ede24b6a3facab73c180678c
[6]	PANDHARD X, SAMSON A. Extension of the SAEM algorithm for nonlinear mixed models with 2 levels of random effects[J]. Biostatistics, 2009, 10(1): 121-135. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_0803.4437
[7]	MENG S X, HUANG S. Improved calibration of nonlinear mixed-effects models demonstrated on a height growth function[J]. Forest Science, 2009, 55(3): 239-248. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=39ee357cfca94197848e4b1076473535
[8]	YANG Y, HUANG S. Comparison of different methods for fitting nonlinear mixed forest models and for making predictions[J]. Canadian Journal of Forest Research, 2011, 41(8): 1671-1686. doi: 10.1139/x11-071
[9]	HEIN S, MÄKINEN H, YUE C, et al. Modelling branch characteristics of Norway spruce from wide spacings in Germany[J]. Forest Ecology & Management, 2007, 242(2-3): 155-164. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=f8db8e620a46053051843fccd9758aee
[10]	HEIN S, WEISKITTEL A R, KOHNLE U. Branch characteristics of widely spaced Douglas-fir in south-western Germany: comparisons of modelling approaches and geographic regions[J]. Forest Ecology & Management, 2008, 256(5): 1064-1079. http://cn.bing.com/academic/profile?id=8cacef1f84fe8e52dd5dab7163b01013&encoded=0&v=paper_preview&mkt=zh-cn
[11]	BEAULIEU E, SCHNEIDER R, BERNINGER F, et al. Modeling jack pine branch characteristics in eastern Canada[J]. Fuel & Energy Abstracts, 2011, 262(9): 1748-1757. http://cn.bing.com/academic/profile?id=f68060386f408f209c6342f7a3b9c252&encoded=0&v=paper_preview&mkt=zh-cn
[12]	LINNELL N A F, PARISHROBERTA, GOUDIEJAMES W. Modelling number, vertical distribution, and size of live branches on coniferous tree species in British Columbia[J]. Canadian Journal of Forest Research, 2012, 42(42): 1072-1090. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=577c6f9204a93dac7b1af00e69fb9168
[13]	KINT V, HEIN S, CAMPIOLI M, et al. Modelling self-pruning and branch attributes for young Quercus robur L. and Fagus sylvatica L. trees[J]. Fuel & Energy Abstracts, 2010, 260(11): 2023-2034. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=860f57b85f95cc5709d4708551c1bf08
[14]	NEMEC A F L, GOUDIE J W, PARISH R. A Gamma-Poisson model for vertical location and frequency of buds on lodgepole pine (Pinus contorta) leaders[J]. Canadian Journal of Forest Research, 2009, 40(40): 2049-2058. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=21370f02b2d0389d23a208619b29b07a
[15]	SATTLER D F, COMEAU P G, ACHIM A. Branch models for white spruce (Picea glauca (Moench) Voss) in naturally regenerated stands[J]. Forest Ecology & Management, 2014, 325: 74-89. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=0e350c83cbe6d90bc1980a067f5b7303
[16]	郭孝玉.长白落叶松人工林树冠结构及生长模型研究[D].北京: 北京林业大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10022-1013215124.htm GUO X Y. Crown structure and growth modle for Larix algersis plantation[D]. Beijing: Beijing Forestry University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10022-1013215124.htm
[17]	郑杨, 董利虎, 李凤日.黑龙江省红松人工林枝条分布数量模拟[J].应用生态学报, 2016, 27(7):2172-2180. http://d.old.wanfangdata.com.cn/Periodical/yystxb201607016 ZHENG Y, DONG L H, LI F R. Branch quantity distribution simulation for Pinus koraiensis plantation in Heilongjiang Province, China[J]. Chinese Journal of Applied Ecology, 2016, 27(7):2172-2180. http://d.old.wanfangdata.com.cn/Periodical/yystxb201607016
[18]	BURNHAM K P, ANDERSON D R, HUYVAERT K P. AIC model selection and multimodel inference in behavioral ecology: some background, observations, and comparisons[J]. Behavioral Ecology & Sociobiology, 2011, 65(1): 23-35. doi: 10.1007-s00265-010-1029-6/
[19]	AHO K, DERRYBERRY D W, PETERSON T. Model selection for ecologists: the worldviews of AIC and BIC[J]. Ecology, 2014, 95(3): 631-636. doi: 10.1890/13-1452.1
[20]	WATSON S P. Poisson regression models for interval censored count data[D/OL].Waco: Baylor University, 2011[2017-03-10].http://gradworks.umi.com/34/56/3456978/html. https://baylor-ir.tdl.org/handle/2104/8176
[21]	ZOU G Y, DONNER A. Extension of the modified Poisson regression model to prospective studies with correlated binary data[J]. Statistical Methods in Medical Research, 2011, 22(6): 661-670. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1177/0962280211427759
[22]	GHITANY M E, KARLIS D, AL-MUTAIRI D K, et al. An EM algorithm for multivariate mixed Poisson regression models and its application[J]. Applied Mathematical Sciences, 2012, 6:6843-6856. http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_4980ae0ae2ec78516b3df003c08fdb15
[23]	ZAMANI H, FAROUGHI P, ISMAIL N. Estimation of count data using mixed Poisson, generalized Poisson and finite Poisson mixture regression models[J]. AIP Conference Proceedings, 2014, 1602(1): 1144-1150. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CC0214576928
[24]	LONG D L, PREISSER J S, HERRING A H, et al. A marginalized zero-inflated Poisson regression model with random effects[J]. Journal of the Royal Statistical Society, 2015, 64(5): 815-830. doi: 10.1111/rssc.12104
[25]	PINHEIRO J C, BATES D M. Mixed-effects models in S and S-PLUS[J]. Journal of the American Statistical Association, 2000, 96(455): 1135-1136. http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_024659aa5aed0dcdbb679c9e020372cc
[26]	BOND B J. Age-related changes in photosynthesis of woody plants[J]. Trends in Plant Science, 2000, 5(8): 349-353. doi: 10.1016/S1360-1385(00)01691-5
[27]	WEISKITTEL A R, MAGUIRE D A, MONSERUD R A. Response of branch growth and mortality to silvicultural treatments in coastal Douglas-fir plantations: implications for predicting tree growth[J]. Forest Ecology & Management, 2007, 251(3): 182-194. http://cn.bing.com/academic/profile?id=af31a4b4e00ff12735a2449538d8c0d5&encoded=0&v=paper_preview&mkt=zh-cn
[28]	WEISKITTEL A R, SEYMOUR R S, HOFMEYER P V. Modelling primary branch frequency and size for five conifer species in Maine, USA[J]. Forest Ecology & Management, 2010, 259(10): 1912-1921. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=6525a57d6fbb2148c9c7838c5bf3a336
[29]	ISHⅡ H, MCDOWELL N. Age-related development of crown structure in coastal Douglas-fir trees[J]. Forest Ecology and Management, 2002, 169(3): 257-270. doi: 10.1016/S0378-1127(01)00751-4
[30]	THORPE H C, ASTRUP R, TROWBRIDGE A, et al. Competition and tree crowns: a neighborhood analysis of three boreal tree species[J]. Forest Ecology & Management, 2010, 259(8): 1586-1596. http://cn.bing.com/academic/profile?id=e01e55e9ca64ee12f100228cbeb0efbf&encoded=0&v=paper_preview&mkt=zh-cn

施引文献(2)

期刊类型引用(1)

徐婷婷，余秋平，漆培艺，刘可慧，李艺，蒋永荣，于方明. 不同淋洗剂对矿区土壤重金属解吸的影响. 广西师范大学学报(自然科学版). 2019(02): 188-193 .

百度学术

其他类型引用(1)

资源附件(0)

图(3) / 表(8)

计量

文章访问数: 3611
HTML全文浏览量: 647
PDF下载量: 74
被引次数: 2

1. 材料与方法
1.1 苗木培育与处理
1.2 样品采集与测定
1.2.1 生理生化指标和元素含量
1.2.2 根系形态特征
1.2.3 生长
1.3 数据处理
2. 结果与分析
2.1 苗木细胞膜透性变化
2.2 可溶性蛋白含量变化
2.3 叶片叶绿素荧光参数变化
2.4 根系形态特征变化
2.5 苗木体内Pb和营养元素含量变化
2.6 生长变化
3. 讨论
3.1 有机酸对Pb胁迫下细胞膜系统的保护作用
3.2 有机酸与Pb胁迫下的渗透调节物质
3.3 叶绿素荧光对Pb胁迫和有机酸的响应
3.4 Pb胁迫、有机酸与植物根系形态、元素吸收和生长
4. 结论

1. 材料与方法
1.1 苗木培育与处理
1.2 样品采集与测定
1.2.1 生理生化指标和元素含量
1.2.2 根系形态特征
1.2.3 生长
1.3 数据处理
2. 结果与分析
2.1 苗木细胞膜透性变化
2.2 可溶性蛋白含量变化
2.3 叶片叶绿素荧光参数变化
2.4 根系形态特征变化
2.5 苗木体内Pb和营养元素含量变化
2.6 生长变化
3. 讨论
3.1 有机酸对Pb胁迫下细胞膜系统的保护作用
3.2 有机酸与Pb胁迫下的渗透调节物质
3.3 叶绿素荧光对Pb胁迫和有机酸的响应
3.4 Pb胁迫、有机酸与植物根系形态、元素吸收和生长
4. 结论

参考文献(30)

施引文献(2)

资源附件(0)

基于Possion回归混合效应模型的长白落叶松一级枝数量模拟

作者简介: 王曼霖。主要研究方向：林分生长与收获模型。Email: 445947011@qq.com 地址: 150040 黑龙江省哈尔滨市和兴路26号东北林业大学林学院

责任作者: 李凤日，教授，博士生导师。主要研究方向：林分生长与收获模型。Email: fengrili@126.com 地址:同上

计量

出版历程