NaOH-乙醇预处理提高甘蔗渣酶法制备低聚木糖效率

杨淑娟; 游艳芝; 张威伟; 王堃; 蒋建新

doi:10.13332/j.1000-1522.20170366

NaOH-乙醇预处理提高甘蔗渣酶法制备低聚木糖效率

北京林业大学材料科学与技术学院，林业生物质材料与能源教育部工程中心，北京 100083

基金项目:

国家重点研发计划课题 2016YFD0600803

详细信息

作者简介:
杨淑娟。主要研究方向：生物质能源及化学品。Email:yang2017bjfu@163.com 地址：100083北京市海淀区清华东路35号北京林业大学材料科学与技术学院

责任作者:
蒋建新，教授，博士生导师。主要研究方向：林产化工及生物质能源材料。Email: jiangjx@bjfu.edu.cn 地址：同上

中图分类号: Q556
计量
- 文章访问数: 2038
- HTML全文浏览量: 467
- PDF下载量: 64
出版历程
- 收稿日期: 2017-10-11
- 修回日期: 2017-11-29
- 发布日期: 2018-01-31

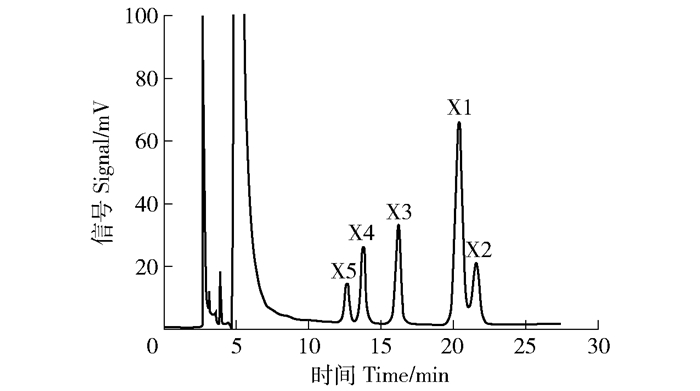
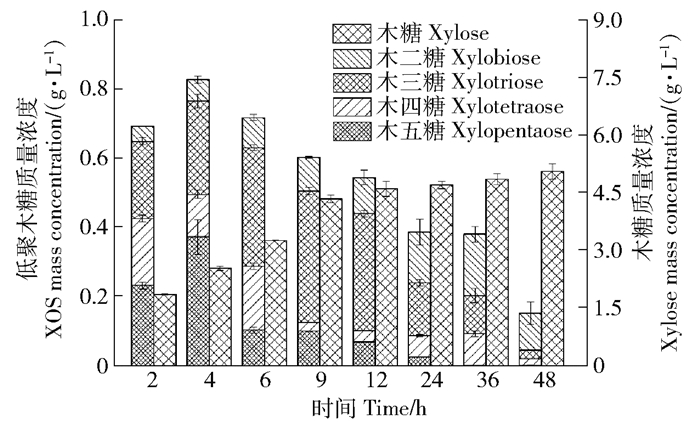
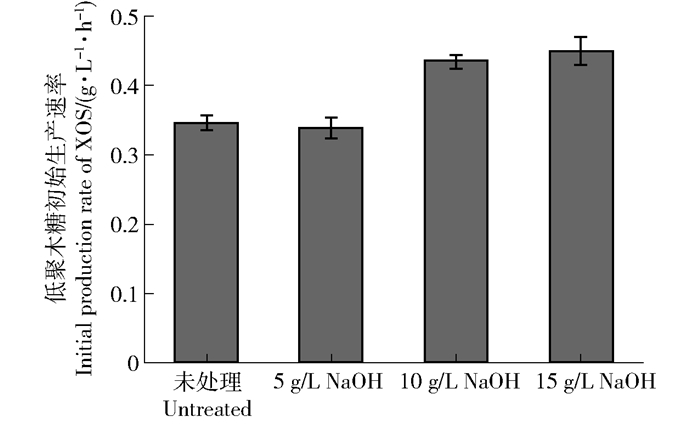
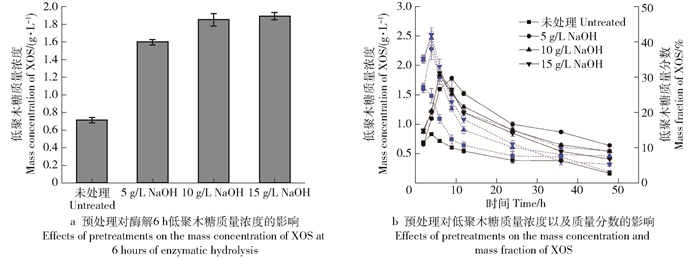
NaOH-ethanol pretreatment increasing preparation efficiency of xylo-oligosaccharide from sugarcane bagasse with enzymatic hydrolysis

College of Materials Science and Technology, Engineering Research Center of Forestry Biomass Material and Bioenergy of Ministry of Education, Beijing Forestry University, Beijing 100083, China

摘要

摘要:
目的对甘蔗渣酶法制备低聚木糖(XOS)的工艺进行研究，并通过NaOH-乙醇预处理提高低聚木糖的生产效率。
方法首先，对预处理前后甘蔗渣的化学组成进行表征，确定预处理对原料组分的影响。其次，利用接触角和X射线衍射分析技术，探讨预处理对底物湿部化学(润湿性)特性和物理结构的影响。最后，通过高效液相色谱(HPLC)分析检测木聚糖酶水解样品，比较不同预处理强度对酶水解生产低聚木糖质量浓度的影响。
结果对于NaOH-乙醇预处理促进木聚糖酶水解的工艺而言，最佳的预处理条件为10 g/L NaOH-乙醇(乙醇的体积分数为50%)预处理。在该预处理强度下，大量的木质素被脱除，脱除率可以达到78.10%；而且，该预处理方式能够有效改善物料的亲水性能，使接触角从61.5°降低到55.4°，同时将纤维原料的结晶度从28.6%提高到32.3%。通过分析酶水解样品可知：当NaOH用量为10 g/L时，可以实现最高低聚木糖质量浓度(1.85 g/L)，与未处理原料(0.83 g/L)相比，提高了122.89%。
结论对于甘蔗渣制备低聚木糖的工艺而言，采用木聚糖酶水解的方式能够实现从半纤维素到低聚木糖的有效转化，并且采用NaOH-乙醇预处理可以有效提高甘蔗渣的酶解效率，促进低聚木糖的生产。
- 甘蔗渣 /
- 预处理 /
- 酶解 /
- 低聚木糖
Abstract:
ObjectiveThe condition of preparation of xylo-oligosaccharide (XOS) from sugarcane bagasse with enzymatic hydrolysis was investigated. In this study, the preparation efficiency of xylo-oligosaccharide was improved by NaOH-ethanol pretreatment.
MethodFirstly, the chemical composition of the sugarcane bagasse before and after pretreatment was characterized, and the effect of pretreatment on the components of the raw material was determined. Secondly, the wettability and physical structure of substrates were characterized by contact angle analysis and X-ray diffraction (XRD). Finally, in order to compare the effects of different pretreatments on the mass concentration of XOS with enzymatic hydrolysis, the enzymatic hydrolysate was harvested and analyzed by high performance liquid chromatography (HPLC).
ResultCharacterization results confirmed that optimal pretreatment condition was 10 g/L NaOH-ethanol (50% v/v ethanol) pretreatment. Under this pretreatment condition, a large amount of lignin was removed and the removal rate of lignin could reach 78.10%. Moreover, the pretreatment could effectively improve the hydrophilicity of raw materials, decreased the contact angle from 61.5° to 55.4°, and also increased the crystallinity of lignocellulose from 28.6% to 32.3%.The results showed that the highest XOS mass concentration was 1.85 g/L after 10 g/L NaOH-ethanol pretreatment, which was 122.89% higher than that of untreated sugarcane bagasse (0.83 g/L).
ConclusionIn the process of XOS preparation from sugarcane bagasse, enzymatic hydrolysis was an efficient way to achieve the conversion from hemicellulose to XOS. NaOH-ethanol pretreatment can effectively increase the efficiency of enzymatic hydrolysis and promote the preparation of XOS.
- sugarcane bagasse /
- pretreatment /
- enzymatic hydrolysis /
- xylo-oligosaccharide

HTML全文

树高和胸径是森林资源调查和经营效果评价的主要林分调查因子，也是林木生长发育和林分材积数量研究的重要变量。树高与胸径关系一直是林学研究的热点。通过量化特定树种的树高与胸径关系拟合树高−胸径预测模型，在计算树干材积、出材率表编制、生长和收获模型、森林资源调查、立地质量评价以及森林碳储量估算方面具有广泛应用。

分位数回归方法具有较长的统计学历史和理论基础，最早于1978年由Koenker等^[1]根据中位数回归推导提出。由于对调查数据模型方差没有严格要求，利用自变量的多个分位数求得因变量条件分布的相应分位数方程，能够描述任意发散点处变量的变化趋势。对具有尖峰、厚尾、异方差显著的数据拟合效果更加稳健^[2]，相对最小二乘回归具有更大优势。已广泛应用于林分自疏边界线、直径分布规律、林分密度指数、林木干形、树冠轮廓以及森林病虫害等领域。国外学者利用分位数回归建立了树高−胸径关系模型^[3]。国内学者利用分位数回归拟合了树冠轮廓^[4]、树冠表面积及树冠体积^[5]，结合哑变量方法构建了大兴安岭落叶松（Larix gmelinii）的树高与胸径关系最优模型^[6]。Cao等^[7]提出利用组合分位数法预测火炬松（Pinus taeda）干形曲线，并通过插值系数修正削度方程以提高预测精度。

树木生长受气候、立地条件和经营措施等多种因素的影响和制约，不同样地间的树高−胸径关系存在较大差异，仅含胸径一个变量的树高模型不能描述不同林况下树高−胸径关系的差异，因此很多引入林分变量或者单木变量构建的广义模型也被用于描述不同林分的模型差异。除此之外，近年来混合效应模型在树高模型中也得到了一定的应用，可以反映总体平均变化趋势及个体之间的变异，不需要假设观测值相互独立^[8]，显著提高了模型的预测精度。Zhang等^[9]在以样地为随机效应的混合模型中引入林分密度和立地指数，结果表明该模型可以显著提高长白落叶松（Larix olgensis）树高−胸径模型的预测精度。燕云飞等^[10]基于广义混合效应构建了拟合效果最优的红松（Pinus koraiensis）人工林枝下高模型。

以往树高−胸径关系研究均选定某种方程进行非线性回归，且对多层次、多树种的混交林树高−胸径关系的描述相比纯林要困难和复杂很多^[11]。同时随着方程通用程度的提高，用于局部地区的误差也会增大^[12]。因此，本研究以吉林蛟河针阔混交林典型树种为研究对象，构建含有林分变量的广义树高−胸径模型，并基于基础模型和广义模型分布拟合不同树种的分位数回归和以样方效应作为分类变量的混合模型，对比分析各树种不同树高−胸径模型的预测效果和拟合差异，为温带针阔混交林资源调查、收获、经营与管理提供依据。

1. 研究区概况与研究方法

1.1 研究区概况

吉林省林业实验区国有林保护中心位于吉林省东部、长白山西麓，隶属于长白山系张广才岭山脉。行政区域处于吉林省蛟河市前进乡境内，属温带大陆性季风气候，年平均气温3.4 ℃，降水量708.8 mm，无霜期为120 ~ 130 d。地貌类型以低山丘陵区为主，海拔459 ~ 517 m。森林资源和植物种类丰富，植被类型为次生针阔混交林，主要乔木树种包括红松、水曲柳（Fraxinus mandshurica）、蒙古栎（Quercus mongolica）、紫椴（Tilia amurensis）、色木槭（Acer mono）、白牛槭（Acer mandshuricum）和胡桃楸（Juglans mandshurica）等。

1.2 数据来源与统计

在研究区设置总面积大小为21.12 hm²监测样地，经纬度为43°57′35″ ~ 43°57′54″N，127°43′37″ ~ 127°44′09″E。2009年对植被开展初次调查，2014年、2019年对样地进行复测。调查时将样地划分为528个20 m × 20 m的连续调查样方，记录所有样方中胸径大于1 cm的木本植物种类，测量胸径、树高、冠幅、坐标、林分郁闭程度等。基于样地内树种组成（表1）和各树种树高−胸径模型的初步拟合结果，选择重要值最高的乔木树种作为研究样本，其中筛选出1 531株红松、3 066株色木槭、1 822株紫椴和1 856株水曲柳。建模时将各组数据随机分成两部分，其中80%作为训练数据，20%作为测试数据（表2）。根据调查数据，计算各样方的林分密度、胸高断面积和优势木高（表3）。在每个20 m × 20 m样方内，分别选择1 ~ 3株最高的林木计算平均值，作为该树种在该样方的优势木高。利用R软件的quantreg包和nlme包进行非线性分位数回归和混合效应模型分析。

表 1 优势树种主要指标统计

Table 1. Main indicator statistics of dominant tree species

树种 Tree species	重要值 Important value	多度 Abundance	频度 Frequency	胸高断面积/（m²·hm⁻²） Basal area/（m²·ha⁻¹）
色木槭 Acer mono	11.42	3 071	505	87.58
水曲柳 Fraxinus mandshurica	11.13	1 861	420	119.81
紫椴 Tilia amurensis	9.46	1 825	472	84.91
红松 Pinus koraiensis	8.21	1 535	411	74.72
暴马丁香 Syringa reticulata	7.28	3 483	466	4.66
春榆 Ulmus davidiana	6.79	2 279	446	26.94
拧筋槭 Acer triflorum	6.51	1 474	444	41.76
蒙古栎 Quercus mongolica	5.62	646	337	55.80
白牛槭 Acer mandshuricum	4.67	1 492	358	15.56
白桦 Betula platyphylla	4.44	876	249	36.81

下载: 导出CSV

| 显示表格

表 2 单木树高−胸径模型拟合及检验数据

Table 2. Fitting and testing data of individual tree height-DBH model

数据分类 Dataset classification	树种 Tree species	样本数 Number of sample	胸径 DBH/cm				树高 Tree height/m
数据分类 Dataset classification	树种 Tree species	样本数 Number of sample	平均值 Mean	最小值 Min. value	最大值 Max. value	标准差 SD	平均值 Mean	最小值 Min. value	最大值 Max. value	标准差 SD
拟合数据 Fitting data	红松 Pinus koraiensis	1 226	19.14	1.60	75.80	15.90	12.25	1.00	33.40	6.75
	色木槭 Acer mono	2 452	14.13	1.20	88.80	12.62	11.22	2.00	37.20	6.10
	紫椴 Tilia amurensis	1 458	19.86	1.20	70.40	13.76	14.42	1.60	32.70	6.36
	水曲柳 Fraxinus mandshurica	1 484	26.17	2.00	75.00	12.32	17.82	2.70	27.30	4.15
检验数据 Testing data	红松 Pinus koraiensis	305	19.28	2.00	65.30	16.12	12.11	1.90	34.40	6.98
	色木槭 Acer mono	614	14.32	1.40	62.00	12.55	11.49	1.20	29.40	6.42
	紫椴 Tilia amurensis	364	20.12	1.70	65.80	14.60	14.45	1.80	34.00	6.68
	水曲柳 Fraxinus mandshurica	372	24.84	1.80	62.40	11.76	17.75	4.50	27.00	4.21

下载: 导出CSV

| 显示表格

表 3 林分调查因子统计表

Table 3. Statistical table of stand description factors

数据分类 Dataset classification	树种 Tree species	胸高断面积/（m²·hm⁻²） Basal area/（m²·ha⁻¹）				林分密度/（株·hm⁻²） Stand density/（tree·ha⁻¹）				优势木高 Dominant tree height/m
数据分类 Dataset classification	树种 Tree species	平均值 Mean	最小值 Min. value	最大值 Max. value	标准差 SD	平均值 Mean	最小值 Min. value	最大值 Max. value	标准差 SD	平均值 Mean	最小值 Min. value	最大值 Max. value	标准差 SD
拟合数据 Fitting data	红松 Pinus koraiensis	32.91	15.10	257.89	13.62	1 223.63	350	2 900	384.76	16.30	1.80	33.40	6.97
	色木槭 Acer mono	32.66	15.02	257.89	17.34	1 244.02	350	3 100	400.18	16.98	4.00	37.20	5.56
	紫椴 Tilia amurensis	34.00	15.02	257.89	14.38	1 284.93	350	2 900	387.05	19.62	3.40	34.00	4.79
	水曲柳 Fraxinus mandshurica	31.44	15.02	257.89	15.41	1 420.70	350	3 100	447.84	24.21	2.80	35.30	4.49
检验数据 Testing data	红松 Pinus koraiensis	33.49	19.21	58.18	7.35	1 215.16	450	2 575	346.34	16.88	2.00	33.40	7.14
	色木槭 Acer mono	33.46	16.19	257.89	16.51	1 258.15	450	2 900	374.19	17.23	3.20	37.20	5.31
	紫椴 Tilia amurensis	33.82	15.02	257.89	16.92	1 310.16	600	2 900	412.81	19.67	6.20	34.00	5.15
	水曲柳 Fraxinus mandshurica	31.91	15.10	257.89	21.16	1 488.58	600	3 100	443.16	24.95	15.20	34.80	3.97

下载: 导出CSV

| 显示表格

1.3 研究方法

1.3.1 基础模型与广义模型

以往大多选定某种非线性方程描述树种的树高−胸径关系，而混交林相对于纯林或年龄结构和林层单一的林分来说，其树高与胸径的关系更为复杂^[13]。根据以往的研究，基于树高−胸径散点图和树种的分布特征，选择以下11个常用的树高模型作为候选基础模型（表4），对树高−胸径分布数据进行非线性拟合，比较各模型的拟合精度，筛选预测精度最高的作为研究区树高−胸径的最优基础模型。

表 4 候选树高−胸径关系模型

Table 4. Candidate models of tree height-DBH relation

模型编号 Model No.	表达式 Equation	参考文献 Reference
M1	$H=1.3 + {\beta }_{1}{D}^{{\beta }_{2}}$	[14]
M2	$H=1.3+\beta_1\left[\dfrac{D}{1+D}\right]^{\beta_2}$	[15]
M3	$H=1.3+\exp\left(\beta_1+\dfrac{\beta_2}{D+1}\right)$	[16]
M4	$H=1.3 + {\beta }_{1}\left[1-\exp\left(-{\beta }_{2}D\right)\right]$	[17]
M5	$H=1.3 + {\beta }_{1}\exp\left(\dfrac{{\beta }_{2}}{D}\right)$	[18]
M6	$H=1.3 + {{\beta }_{1}[1-\exp(-{\beta }_{2}D\left)\right]}^{{\beta }_{3}}$	[19]
M7	$H=1.3 + {\beta }_{1}{D}^{\left[{\beta }_{2}{D}^{(-{\beta }_{3})}\right]}$	[20]
M8	$H=1.3+\exp\left(\beta_1+\dfrac{\beta_2}{D+\beta_3}\right)$	[21]
M9	$H=1.3 + {\beta }_{1}\exp\left[-{\beta }_{2}\exp\left(-{\beta }_{3}D\right)\right]$	[22]
M10	$H=1.3+\dfrac{D^2}{\beta_1+\beta_2D+\beta_3D^2}$	[23]
M11	$H=1.3+\dfrac{\beta_1}{1+\beta_2\exp\left(-\beta_3D\right)}$	[24]
注：H为树高预测值；D为胸径；β₁、β₂、β₃为模型参数。Notes: H is the predicted tree height; D is the DBH; β₁, β₂ and β₃ are the model parameters.

下载: 导出CSV

| 显示表格

但在结构更加复杂的针阔混交林中，仅仅将胸径作为预测变量，无法反映其他林分变量对树高的影响。本研究采用再参数化的方法建立树高−胸径模型，依据林分变量与树高之间的关系，适当融合林分密度、胸高断面积和优势木高度等变量。具体做法如下：基于所选择的最优基础模型，对林分变量与树高进行相关性分析；比较不同变量引入对模型的影响，筛选模型中的其他变量，确定与树高相关性较大且能显著提高模型预测能力的变量作为协变量；基于最优基础模型构建各树种预测精度最高的广义模型。

1.3.2 分位数回归

分位数回归是利用解释变量估计响应变量的条件分位数分布，全面刻画整个条件分布的综合回归方法^[25−26]。不仅可以度量响应变量对分布中心的影响，而且可以度量对分布上尾和下尾的影响。最小二乘法假定误差服从正态分布，而分位数回归的响应变量的平均预测值对残差分布没有特殊要求^[27]，从而确保参数估计的稳健性和模型拟合的灵活性。最小二乘回归的目标是最小化误差平方和，分位数回归的核心思想是从均值推广到分位数，也是通过最小化残差绝对值的非对称损失函数来估计分为点处参数值。

$\min\left[{\sum} _{{y}_{\tau }\geqslant {\hat{y}}_{\tau }}\tau \left({y}_{\tau }-{\hat{y}}_{\tau }\right) + {\sum} _{{y}_{\tau } < {\hat{y}}_{\tau }}(1-\tau )\left({\hat{y}}_{\tau }-{y}_{\tau }\right)\right]$

(1)

式中：τ表示要估计的分位数， ${y}_{\tau }$ 和 ${\hat{y}}_{\tau }$ 分别为响应变量在分位数τ处的观测值和估计值。

分位数组合法利用抽样数据拟合不同组合的分位数曲线，基于相邻两条分位数回归曲线插值得到修正的分位数曲线。假设第i个样方第j个树木的胸径值为 ${x}_{ij}$ ，树高观测值为 ${y}_{ij}$ 分布在第m和（m + 1）分位数估计值之间，即 ${\hat{y}}_{m}\left({x}_{ij}\right)$ ≤ ${y}_{ij}$ ≤ ${\hat{y}}_{m + 1}\left({x}_{ij}\right)$ 。使用插值法计算通过该点的修正曲线。

${\hat{y}}_{ij}=\alpha {\hat{y}}_{m}\left({x}_{ij}\right) + (1-\alpha ){\hat{y}}_{m + 1}\left({x}_{ij}\right)$

(2)

式中： $\alpha$ = $\dfrac{{\hat{y}}_{m + 1}\left({x}_{ij}\right)-{y}_{ij}}{{\hat{y}}_{m + 1}\left({x}_{ij}\right)-{\hat{y}}_{m}\left({x}_{ij}\right)}$ 表示插值系数， ${\hat{y}}_{ij}$ 为树高估计值， ${\hat{y}}_{m}\left({x}_{ij}\right)\mathrm{和}{\hat{y}}_{m + 1}\left({x}_{ij}\right)$ 分别为胸径为 ${x}_{ij}$ 的树木在第m和（m + 1）分位数处的树高估计值。

当抽样数量大于1时，在各分位数组合中选择使平均误差值符号发生改变的相邻曲线。当胸径值大于最大分位数回归的预测值时，将 $\hat{y}$ _m和 $\hat{y}$ _{m + 1}分别定义为 $\hat{y}$ _{m − 1}和 $\hat{y}$ _m，之后利用公式（2）得到树高曲线。

由于基础模型只有一个预测变量缺乏其他变量信息，很难完整描述响应变量在不同分位点的分布。本研究选择9个分位点（τ = 0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9），基于所选的最优基础模型拟合树高−胸径曲线，同时使用三分位数、五分位数和九分位数组合法得到树高修正曲线，通过模型评价和比较得到基于最佳分位数的基础模型，进而在该模型中融入林分变量构建广义分位数模型。

1.3.3 非线性混合效应模型

在筛选出的最优基础模型和广义模型加入随机效应构建非线性混合模型，本研究中选择样方为随机效应，混合效应模型一般形式可表示为

$\hat{\boldsymbol{H}}_{ij}=f\left(\hat{\boldsymbol{\phi}}_i,\hat{\boldsymbol{D}}_{ij}\right)+\boldsymbol{\varepsilon}_{ij},\ {\boldsymbol{\varepsilon}}_{ij}\sim{{{{\rm{N}}}}}(0,\ \sigma^2)$

(3)

式中： $\hat{\boldsymbol{H}}_{ij}$ 和 $\hat{\boldsymbol{D}}_{ij}$ 分别为第i个样方第j株树的树高和胸径预测向量，f为包含树高和胸径变量的函数表达式， $\hat{\boldsymbol{\phi}}_i$ 为混合效应参数向量，ε_ij为误差项。

参数向量 $\hat{\boldsymbol{\phi}}_i$ 的固定效应参数和随机效应参数可表示为

${\boldsymbol{\phi}}_i=\hat{\boldsymbol{X}}_i \hat{\boldsymbol{\beta}}+ {\hat{\boldsymbol{Z}}_i} {\hat{\boldsymbol{u}}_i},\; {\hat{\boldsymbol{u}}_i} \sim {\text{N}}(0,\; {\text{φ}})$

(4)

式中： $\hat{\boldsymbol{\beta }}$ 为固定效应参数向量， ${\hat{\boldsymbol{u}}}_{i}$ 为第i个样方的随机效应参数向量，遵循均值为0、协方差矩阵为 ${\text{φ}}$ 的正态分布， ${\hat{\boldsymbol{X}}}_{i}$ 和 ${\hat{\boldsymbol{{Z}}}}_{i}$ 分别是 $\hat{\boldsymbol{\beta }}$ 和 ${\hat{\boldsymbol{u}}}_{i}$ 的设计矩阵。

非线性混合效应模型中，方差−协方差结构由包括相关因子和加权因子的矩阵R_i来表示。

${\boldsymbol{R}}_{i}={\sigma }^{2}{\boldsymbol{G}}_{i}^{0.5}{\boldsymbol{\varGamma }}_{i}{\boldsymbol{G}}_{i}^{0.5}$

(5)

式中：σ²指模型的残差方差值，Γ_i为组内误差相关性结构，G_i为描述样方内方差异质性的对角矩阵，其对角元素由方差函数提供^[28]。

随机效应的方差−协方差结构（D）反映了样方间的差异，矩阵因随机参数个数的不同也会有不同的形式，本研究中选用广义正定矩阵结构，当混合模型中具有两个随机参数时表达式如下

$\boldsymbol{D}=\left[\begin{array}{cc}{\sigma }_{{u}_{1}}^{2}& {\sigma }_{{u}_{1}{u}_{2}}\\ {\sigma }_{{u}_{1}{u}_{2}}& {\sigma }_{{u}_{2}}^{2}\end{array}\right]$

(6)

式中： ${u}_{1}$ 、 ${u}_{2}$ 为随机参数， ${\sigma }_{{u}_{1}}^{2}$ 、 ${\sigma }_{{u}_{2}}^{2}$ 分别为 ${u}_{1}$ 、 ${u}_{2}$ 的方差， ${\sigma }_{{u}_{1}{u}_{2}}$ 为 ${u}_{1}$ 和 ${u}_{2}$ 的协方差。

混合效应模型中固定效应部分的检验方法与传统模型相同，对于随机效应的检验则需要计算随机参数值，本研究需计算在拟合数据中不涉及的样方的随机参数，利用式7^[29]进行计算。

$\hat{u}_i\approx\hat{D}\hat{Z}_i^{\mathrm{T}}\left(\hat{Z}_i\hat{D}\hat{Z}_i^{\mathrm{T}}+\hat{R}_i\right)^{-1}\hat{e}_i$

(7)

式中： $\hat{\boldsymbol{D}}$ 为随机效应参数的方差协方差矩阵， ${\hat{\boldsymbol{R}}}_{i}$ 为样方内方差协方差矩阵， ${\hat{\boldsymbol{Z}}}_{i}$ 为设计矩阵， ${\hat{\boldsymbol{Z}}}_{i}^{\mathrm{T}}$ 为转置矩阵， ${\hat{e}}_{i}$ 为实际值减去用固定效应参数计算的预测值。

1.3.4 模型评价与检验

研究中通过决定系数（R²）、平均绝对误差（MAE）和均方根误差（RMSE）评价和比较模型拟合结果，并利用未参与建模的20%独立样本检验11个候选非线性模型，上述评价指标的计算公式。

${R}^{2}=1-{\sum} _{i,j=1}^{n}{\left({H}_{ij}-{\hat{H}}_{ij}\right)}^{2}/{\sum} _{i,j=1}^{n}{\left({H}_{ij}-{\overline{H}}_{ij}\right)}^{2}$

(8)

$\mathrm{M}\mathrm{A}\mathrm{E}={\sum} _{i,j=1}^{n}\left|{H}_{ij}-{\hat{H}}_{ij}\right|/n$

(9)

$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\sum} _{i,j=1}^{n}{\left({H}_{ij}-{\hat{H}}_{ij}\right)}^{2}/n}$

(10)

式中： ${H}_{ij}$ 和 ${\hat{H}}_{ij}$ 为第i个样方第j个样本的树高实际值和预测值， ${\overline{H}}_{ij}$ 为预测值的均值；n 为样本数。

除考虑以上指标外，还选择赤池信息准则（AIC）、贝叶斯信息准则（BIC）和似然比检验（LRT）对混合效应模型进行评价，AIC和BIC数值越小则表明模型拟合精度越高，LRT得到的P值若 < 0.000 1，则认为两个模型差异显著。

$\mathrm{AIC}=-2\mathrm{\mathit{L}}+2\lambda$

(11)

$\mathrm{BIC}=-2\mathrm{\mathit{L}}+\lambda\mathrm{ln}\ n$

(12)

式中：L为模型的对数似然值，λ 为固定效应参数的个数。

2. 结果与分析

2.1 基础模型拟合

基于红松、色木槭、紫椴和水曲柳的建模数据，对表4中的11个基础模型进行拟合，比较其MAE、RMSE和R²值（表5）。结果表明，对于4个树种的树高−胸径关系拟合，各模型均具有良好表现。MAE范围为1.887 ~ 2.818，RMSE范围为2.557 ~ 3.582，R²则为0.552 ~ 0.811，其中红松、紫椴水曲柳以M6即Richards模型拟合结果最优，色木槭的Richards模型拟合结果与其最优模型相差极小。使用检验数据对拟合模型进行评价比较，得到相同结果。且Richards方程生物学意义明确、灵活性较高易收敛，被认为很适合描述树高与胸径之间的关系^[30−31]，因此选择Richards作为4个树种的基础模型。

表 5 候选模型拟合与评价

Table 5. Fitting and evaluation of candidate models

模型 Model	红松 Pinus koraiensis			色木槭 Acer mono			紫椴 Tilia amurensis			水曲柳 Fraxinus mandshurica
模型 Model	MAE	RMSE	R²	MAE	RMSE	R²	MAE	RMSE	R²	MAE	RMSE	R²
M1	2.381	3.153	0.780	2.118	2.846	0.781	2.818	3.582	0.684	2.248	2.774	0.552
M2	2.361	3.128	0.784	2.080	2.806	0.787	2.521	3.357	0.722	2.079	2.571	0.615
M3	2.211	2.982	0.803	1.926	2.697	0.803	2.503	3.344	0.724	2.083	2.575	0.614
M4	2.179	2.945	0.808	1.895	2.654	0.809	2.530	3.343	0.724	2.088	2.575	0.614
M5	2.279	3.032	0.797	2.030	2.772	0.793	2.547	3.374	0.719	2.076	2.568	0.616
M6	2.140	2.925	0.811	1.890	2.654	0.809	2.491	3.332	0.726	2.063	2.557	0.619
M7	2.149	2.936	0.809	1.887	2.653	0.809	2.495	3.337	0.725	2.069	2.562	0.617
M8	2.144	2.932	0.810	1.888	2.652	0.810	2.496	3.335	0.725	2.074	2.565	0.617
M9	2.174	2.945	0.808	1.931	2.691	0.804	2.513	3.348	0.723	2.077	2.570	0.615
M10	2.146	2.935	0.809	1.887	2.652	0.810	2.493	3.336	0.725	2.068	2.560	0.618
M11	2.231	2.991	0.802	1.986	2.742	0.796	2.553	3.381	0.718	2.091	2.587	0.610
注：MAE.平均绝对误差；RMSE.均方根误差；R².决定系数。下同。Notes: MAE, mean absolute error; RMSE, root mean squared error; R², coefficient of determination. The same below.

下载: 导出CSV

| 显示表格

2.2 广义模型构建

对表3的林分特征因子进行相关性分析，结果如表6所示。4个树种的树高和胸径与优势木高呈显著正相关关系（P < 0.01），色木槭和紫椴树高、胸径与林分密度呈显著负相关关系（P < 0.01）。因此将优势木高和林分密度两个变量分别引入基础模型构建广义模型，但包含林分密度因子的色木槭和紫椴树高方程不收敛，而引入胸高断面积的水曲柳树高方程也不收敛，这表明添加优势木高度可显著提高模型精度。因此本研究最优广义模型的表达式为

表 6 树高与林分变量相关性分析

Table 6. Correlation analysis between tree height and stand variables

树种 Tree species	因子 Factor	树高 Tree height	胸径 DBH	胸高断面积 Basal area	林分密度 Stand density	优势木高 Dominate tree height
红松 Pinus koraiensis	树高 Tree height	1.000
	胸径 DBH	0.855^**	1.000
	胸高断面积 Basal area	0.020	0.040	1.000
	林分密度 Stand density	0.010	0.006	0.092^**	1.000
	优势木高 Dominate tree height	0.587^**	0.440^**	0.069^*	0.018	1.000
色木槭 Acer mono	树高Tree height	1.000
	胸径 DBH	0.845^**	1.000
	胸高断面积 Basal area	0.031	0.030	1.000
	林分密度 Stand density	−0.284^**	−0.270^**	0.089^**	1.000
	优势木高 Dominate tree height	0.484^**	0.353^**	0.139^**	−0.261^**	1.000
紫椴 Tilia amurensis	树高 Tree height	1.000
	胸径 DBH	0.776^**	1.000
	胸高断面积 Basal area	0.068^**	0.064^**	1.000
	林分密度 Stand density	−0.207^**	−0.200^**	0.105^**	1.000
	优势木高 Dominate tree height	0.537^**	0.294^**	0.178^**	−0.175^**	1.000
水曲柳 Fraxinus mandshurica	树高Tree height	1.000
	胸径 DBH	0.684^**	1.000
	胸高断面积 Basal area	0.067^**	0.133^**	1.000
	林分密度 Stand density	−0.037	−0.081^**	0.084^**	1.000
	优势木高 Dominate tree height	0.256^**	0.264^**	−0.021^**	0.318^**	1.000
注：^** 表示两个变量在 P < 0.01 水平上显著相关，^* 表示两个变量在 P < 0.05 水平上显著相关。Notes:^** means significant correlation at P < 0.01 level between two variables, ^* means significant correlation at P < 0.05 level between two variables.

下载: 导出CSV

| 显示表格

$H=1.3+(\beta_1+a_1H_{\mathrm{D},i})\left[1-\exp\left(-\beta_2D\right)\right]^{\beta_3}$

(13)

式中：H_D为某个树种的优势木高，H_D,i为第i个样方的优势木高， ${\beta }_{1}$ 、 ${\beta }_{2}$ 、 ${\beta }_{3}$ 、 ${a}_{1}$ 为模型参数。

2.3 分位数回归

在不同分位点处（τ = 0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9），基于Richards方程利用分位数回归分别拟合树高−胸径关系模型（表5）。利用回归评价指标检验不同分位数模型对观测值的拟合程度（表7），基础模型及分位数回归模型的决定系数R²值均在0.6以上，表明各分位点的树高方程均具有较好的拟合效果。其中τ = 0.5的中位数回归与非线性回归的拟合效果基本一致，反映了分位数回归模型的灵活性。

表 7 分位数回归模型拟合精度

Table 7. Goodness-of-fit tests for quantile regression models

分位数 Quantile	红松 Pinus koraiensis			色木槭 Acer mono			紫椴 Tilia amurensis			水曲柳 Fraxinus mandshurica
分位数 Quantile	MAE	RMSE	R²	MAE	RMSE	R²	MAE	RMSE	R²	MAE	RMSE	R²
Richards	2.140	2.925	0.811	1.890	2.654	0.809	2.491	3.332	0.726	2.063	2.557	0.619
0.1	3.415	4.497	0.780	3.103	4.105	0.770	4.029	5.166	0.696	3.426	4.156	0.614
0.2	2.779	3.826	0.793	2.460	3.406	0.793	3.140	4.238	0.715	2.680	3.387	0.615
0.3	2.368	3.322	0.805	2.081	2.963	0.804	2.742	3.791	0.720	2.323	2.976	0.615
0.4	2.179	3.063	0.809	1.924	2.764	0.807	2.520	3.493	0.723	2.116	2.693	0.615
0.5	2.122	2.942	0.811	1.873	2.666	0.809	2.461	3.374	0.724	2.056	2.583	0.617
0.6	2.191	2.953	0.810	1.918	2.675	0.808	2.542	3.363	0.724	2.119	2.596	0.616
0.7	2.440	3.181	0.807	2.161	2.897	0.803	2.830	3.630	0.719	2.372	2.846	0.614
0.8	2.912	3.690	0.797	2.577	3.354	0.791	3.388	4.268	0.697	2.887	3.422	0.615
0.9	4.081	5.027	0.753	3.451	4.293	0.762	4.629	5.519	0.679	3.965	4.582	0.602

下载: 导出CSV

| 显示表格

利用未参与建模的20%测试数据检验模型的预测能力（表8）。分位数组合法分别采用三分位数组合（τ = 0.1，0.5，0.9）、五分位数组合（τ = 0.1，0.3，0.5，0.7，0.9）和九分位数组合（τ = 0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9）。随机抽样或抽取平均木时幼树会带来较大预测误差，基于王君杰等^[32]的研究结果，选取10株最大树木计算插值系数进行预测。结果表明：对于分位数组合法，三分位数和五分位数组合的预测精度高于九分位数组合；其中红松树高的拟合效果略优于中位数回归，但其他树种模型预测精度均低于中位数回归。因此，本研究选择中位数为4个树种的最优分位数树高曲线式（13）构建广义分位数模型。

表 8 分位数模型验证评价结果

Table 8. Quantile model validation evaluation results

方法 Method	红松 Pinus koraiensis		色木槭 Acer mono		紫椴 Tilia amurensis		水曲柳 Fraxinus mandshurica
方法 Method	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE
中位数回归 Median regression	2.963	2.094	2.898	2.020	3.540	2.549	2.560	2.050
九分位数组合 Nine quantile combination	2.956	2.118	2.997	2.185	3.510	2.761	2.601	2.150
五分位数组合 Five quantile combination	2.927	2.095	2.971	2.155	3.507	2.758	2.602	2.152
三分位数组合 Triquartile combination	2.926	2.092	2.983	2.162	3.596	2.851	2.592	2.139

下载: 导出CSV

| 显示表格

表 11 树高−胸径模型拟合评价统计量

Table 11. Fitting and evaluation statistics of tree height-DBH models

树种 Tree species	指标 Index	基础模型 Base model	广义模型 Generalized model	中位数回归 Median quantile regression		非线性混合效应 Nonlinear mixed-effects
树种 Tree species	指标 Index	基础模型 Base model	广义模型 Generalized model	简单模型 Simple model	广义模型 Generalized model	简单模型 Simple model	广义模型 Generalized model
红松 Pinus koraiensis	MAE	2.140	1.669	2.122	1.666	1.259	1.358
	RMSE	2.925	2.225	2.942	2.228	1.687	1.826
	R²	0.811	0.891	0.811	0.891	0.937	0.927
色木槭 Acer mono	MAE	1.890	1.575	1.873	1.568	1.258	1.359
	RMSE	2.654	2.159	2.666	2.166	1.740	1.875
	R²	0.809	0.875	0.809	0.874	0.919	0.906
紫椴 Tilia amurensis	MAE	2.491	1.722	2.461	1.706	1.399	1.611
	RMSE	3.332	3.379	3.374	2.401	1.955	2.235
	R²	0.726	0.860	0.724	0.858	0.906	0.877
水曲柳 Fraxinus mandshurica	MAE	2.063	2.041	2.056	2.031	2.004	2.527
	RMSE	2.557	2.524	2.583	2.536	2.478	2.038
	R²	0.619	0.629	0.617	0.627	0.643	0.629

下载: 导出CSV

| 显示表格

2.4 非线性混合效应模型构建

在基础模型和广义模型基础上考虑样方效应对树高的影响，在4个树种的基础模型上增加样方为随机效应，共8种情况收敛（表9），红松、紫椴和水曲柳增加1个随机效应参数时拟合效果最好，而色木槭引入2个随机参数的混合模型预测精度更高，模型表达式分别为

表 9 混合效应模型验证评价结果

Table 9. Verification and evaluation results of mixed effect model

树种 Tree species	基础混合效应模型 Base mixed-effect model						广义混合效应模型 Generalized mixed-effect model
树种 Tree species	随机参数 Random parameter	AIC	BIC	L	LRT	P	随机参数 Random parameter	AIC	BIC	L	LRT	P
红松 Pinus koraiensis	${u}_{1}$	5 619.3	5 644.8	−2 804.6			${u}_{1}$	5 346.9	5 377.5	−2 667.4
	${u}_{1}$ , ${u}_{2}$	5 643.2	5 678.9	−2 814.6	19.878 2	< 0.001	${u}_{3}$	5 354.2	5 384.8	−2 671.1
							${u}_{1}$ , ${u}_{3}$	5 350.9	5 391.8	−2 667.5	7.238 0	0.026 8
色木槭 Acer mono	${u}_{2}$	10 966.2	10 995.2	−5 478.1			${u}_{1}$	10 597.5	10 632.3	−5 292.7
	${u}_{1}$ , ${u}_{2}$	10 962.2	11 002.9	−5 474.1	7.964 9	0.018 6	${u}_{3}$	10 602.8	10 637.6	−5 295.4
							${u}_{1}$ , ${u}_{3}$	10 594.2	10 640.6	−5 289.1	12.571 9	0.001 9
							${u}_{1}$ , ${u}_{2}$	10 601.4	10 647.8	−5 292.8
紫椴 Tilia amurensis	${u}_{1}$	7 109.6	7 136.0	−3 549.8			${u}_{1}$	6 662.5	6 694.2	−3 325.2
							${u}_{3}$	6 661.8	6 693.5	−3 324.9
							${u}_{1},{u}_{3}$	6 665.8	6 708.0	−3 324.9	4.415 0	0.998 7
水曲柳 Fraxinus mandshurica	${u}_{1}$	7 007.8	7 034.4	−3 498.9			${u}_{1}$	6 966.0	6 997.8	−3 477.0
	${u}_{2}$	7 009.0	7 035.5	−3 499.5			${u}_{3}$	6 964.3	6 996.1	−3 476.1
	${u}_{1}$ , ${u}_{2}$	7 011.8	7 049.0	−3 498.9	1.126 9	0.569 2	${u}_{1},{u}_{3}$	6 964.9	7 007.4	−3 474.5	3.322 9	0.189 9
注：AIC.赤池信息准则；BIC.贝叶斯信息准则；L.对数似然值；LRT.似然比检验。Notes: AIC, Akaike information criterion; BIC, Bayesian information criterion; L, log-likelihood value; LRT, likelihood ratio test.

下载: 导出CSV

| 显示表格

$H=1.3 + {({\beta }_{1} + {u}_{1i})[1-\exp(-{\beta }_{2}D\left)\right]}^{{\beta }_{3}}$

(14)

$H=1.3 + {({\beta }_{1} + {u}_{1i})[1-\exp(-{\beta }_{2}D\left)\right]}^{{(\beta }_{3 + }{u}_{2i})}$

(15)

式中： ${u}_{1i}$ 、 ${u}_{2i}$ 为样方水平的随机参数。

在广义模型基础上，引入不同组合形式的随机效应作为自变量构建广义混合效应模型，4个树种共有13种情况收敛（），当引入3个以上随机参数时，模型不收敛；仅引入参数 ${u}_{1}$ 的红松树高模型和仅引入参数 ${u}_{3}$ 的紫椴及水曲柳树高模型AIC、BIC值最小，且L值达到最大，而色木槭以随机效应作用于 ${u}_{1}$ 和 ${u}_{3}$ 两个参数时模型预测精度最高，一般表达式分别为

$H=1.3+(\beta_1+u_{1i}+a_1H_{\mathrm{D},\mathit{\mathrm{\mathit{i}}}})\left[1-\exp\left(-\beta_2D\right)\right]^{\beta_3}$

(16)

$H=1.3+\left[\beta_1+u_{1i}+(a_1+u_{3i})H_{\mathrm{D},\mathrm{\mathit{i}}}\right]\left[1-\exp\left(-\beta_2D\right)\right]^{\beta_3}$

(17)

$H=1.3+\left[\beta_1+(a_1+u_{3i})H_{\mathrm{D},\rm{\mathit{i}}}\right]\left[1-\exp\left(-\beta_2D\right)\right]^{\beta_3}$

(18)

式中： ${u}_{1i}$ 、 ${u}_{3i}$ 为样方水平的随机参数。

选择各树种拟合效果最好的混合效应模型，参数估计值见表10。

表 10 混合效应模型参数估计

Table 10. Parameter estimates of mixed-effect models

参数 Parameter	基础混合效应模型 Base mixed-effect model				广义混合效应模型 Generalized mixed-effect model
参数 Parameter	红松 Pinus koraiensis	色木槭 Acer mono	紫椴 Tilia amurensis	水曲柳 Fraxinus mandshurica	红松 Pinus koraiensis	色木槭 Acer mono	紫椴 Tilia amurensis	水曲柳 Fraxinus mandshurica
公式编号 Equation No.	（14）	（15）	（14）	（14）	（16）	（17）	（18）	（18）
a	21.192（0.387^***）	18.626（0.251^***）	19.366（0.263^***）	20.021（0.190^***）	9.186（0.535^***）	7.776（0.467^***）	4.522（0.468^***）	16.513（0.523^***）
b	0.065（0.004^***）	0.085（0.004^***）	0.100（0.005^***）	0.101（0.007^***）	0.071（0.004^***）	0.092（0.004^*）	0.104（0.005^***）	0.110（0.007^***）
c	1.366（0.056^***）	1.142（0.033^***）	1.367（0.066^***）	1.445（0.126^***）	1.305（0.057^***）	1.142（0.034^***）	1.322（0.066^***）	1.567（0.142^***）
a₁					0.577（0.024^***）	0.554（0.023^***）	0.715（0.022^***）	0.132（0.019^***）
${\mathrm{\sigma }}_{{u}_{1}}^{2}$	14.927 2	10.920 5	11.410 7	0.201 9	2.877 0	14.850 5
${\mathrm{\sigma }}_{{u}_{2}}^{2}$		0.011 9
${{\mathrm{\sigma }}^{2}}_{{u}_{3}}$						0.038 0	0.001 7	0.000 4
${\mathrm{\sigma }}_{{u}_{1}{u}_{2}}$		0.162 1
${\mathrm{\sigma }}_{{u}_{1}{u}_{3}}$						−0.718 2
${\mathrm{\sigma }}^{2}$	3.637 0	3.638 8	4.908 0	6.422 3	3.811 3	3.858 9	5.275 9	6.201 5
注：^*表示在 P < 0.001 水平上显著。Note: ^* means significant at P < 0.001 level.

下载: 导出CSV

| 显示表格

2.5 模型评价与检验

4个树种的各模型拟合统计量见表11。结果表明：基于混合效应的模型精度明显高于不含随机参数的模型；在不含随机效应的模型中，中位数回归形式和一般形式的广义模型精度差异较小；广义中位数模型在预测精度上高于基础模型的中位数回归，红松、色木槭、紫椴和水曲柳的模型R²分别提高了9.9%、8.0%、18.5%和1.6%，MAE值分别降低了27.4%、19.5%、44.3%和1.2%，RMSE值分别下降了32.0%、23.1%、40.5%和1.9%。在增加随机效应的模型中，基础混合模型的拟合结果略优于广义混合模型，4个树种R²仅分别提高了1.1%、1.4%、3.3%和2.2%，但两者并未有显著差异。红松、色木槭、紫椴和水曲柳的基础混合效应和广义混合效应模型的残差分布图如图1所示，残差分布较为均匀，没有出现明显的不规则形状，这说明各树种的混合模型均没有明显异方差现象。

图 1 基础混合效应模型（A1、B1、C1、D1）和广义混合效应模型（A2、B2、C2、D2）的残差分布图

Figure 1. Residual plots of base mixed-effect models (A1, B1, C1, D1) and generalized mixed-effect models (A2, B2, C2, D2)

下载: 全尺寸图片幻灯片

混合效应模型中随机效应部分的检验需要估算随机参数值，本研究以20%的样木作为检验数据，利用公式（7）分别计算未包含在拟合数据的样方的随机参数；同时与基础模型、广义模型和分位数模型的预测精度进行比较，检验结果如表12。可以看出，混合效应模型的MAE和RMSE值均小于其他模型，拟合效果相较分位数回归得到了显著提高，其中基础混合模型相比于广义混合模型预测精度更高。

表 12 树高−胸径模型统计检验

Table 12. Goodness-of-fit statistics of tree height-DBH models

树种 Tree species	指标 Index	基础模型 Base model	广义模型 Generalized model	中位数回归 Median quantile regression		非线性混合效应 Nonlinear mixed-effects
树种 Tree species	指标 Index	基础模型 Base model	广义模型 Generalized model	简单模型 Simple model	广义模型 Generalized model	简单模型 Simple model	广义模型 Generalized model
红松 Pinus koraiensis	MAE	2.128	2.119	2.094	2.163	1.600	1.856
红松 Pinus koraiensis	RMSE	2.963	3.024	2.963	3.063	2.216	2.635
色木槭 Acer mono	MAE	2.018	1.906	2.020	2.052	1.620	1.712
色木槭 Acer mono	RMSE	2.867	2.782	2.898	2.944	2.341	2.529
紫椴 Tilia amurensis	MAE	2.571	1.685	2.549	2.697	1.609	1.635
紫椴 Tilia amurensis	RMSE	3.471	2.349	3.540	3.754	2.058	2.206
水曲柳 Fraxinus mandshurica	MAE	2.041	2.037	2.050	2.051	2.039	2.049
水曲柳 Fraxinus mandshurica	RMSE	2.526	2.517	2.560	2.561	2.528	2.534

下载: 导出CSV

| 显示表格

3. 讨　　论

3.1 基于基础模型的分位数回归

分位数回归既能描述均值条件下树高的分布趋势，也能描述特定分位点树高−胸径曲线的形状变化^[33]。传统的最小二乘法易受残差分布限制，与之相比分位数回归具有更加稳健的参数估计值，模型稳定性和灵活性也更强，能够避免选取数据的人为影响。在不同分位点拟合树高−胸径模型，同时基于参数估计和建模样本计算三分位数、五分位数和九分位数组合的插值系数，王君杰等^[34]最近发现中位数回归优于非线性回归；本文与之不同发现中位数回归与非线性回归的拟合效果基本一致。经过对11个非线性模型的评价比较，选择Richards方程作为基础模型进行分位数回归，其中中位数回归拟合效果最好，4个树种的R²值均大于0.6，对树高的预测能力不逊于非线性回归，这表明Richards方程能广泛适用树高−胸径模型的拟合。

三分位数组合的预测效果均优于五分位数和九分位数组合，尤其在红松树高的预测中，两类分位数组合的预测精度相较中位数和非线性回归均有提高；以往研究显示五分位数组合对树高曲线和削度方程的拟合要优于三分位数组合，但都没有考虑抽取方案对分位数组合的影响^[35]。因此抽取方案的不同会导致分位数组合之间的差异不同，总体上三分位数组合（τ = 0.1，0.5，0.9）的预测能力较好且效果稳定，本研究中选取多个分位数组合也并未使预测结果有明显提高^[32]。

3.2 引入林分变量和随机效应对树高模型的影响

在林分生长过程中，有学者利用含有优势木胸径、树高和林分密度等因子的模型来描述树高−胸径关系，模型拟合结果得到提升^[36]。为了比较不同样方间树高−胸径的变化规律，本研究对胸高断面积、林分密度和优势木高3个林分变量进行Pearson相关性分析，发现引入变量的广义模型的拟合效果均优于基础模型，当引入1个变量时，红松、色木槭、紫椴和水曲柳均仅增加优势木高变量的模型可以收敛，部分其他林分变量与树高有显著关系，但含优势木高的模型相较含林分密度或胸高断面积的广义模型对树高−胸径的关系影响更大；4个树种中水曲柳的广义模型相较基础模型的拟合效果提升幅度最小，R²仅提高0.01，这可能与水曲柳的直径分布有关，幼树数量较少，成熟林木较多，在林分中多位于林冠层，内部资源和空间竞争相对稳定，处于优势地位，这类大个体的树高不易受林分变量较大影响。这说明即使是在具有相似地形和气候条件的林分中，不同树种的树高−胸径关系可能不同。森林群落中特定的环境条件和树木之间的复杂联系可能会导致树高−胸径生长关系不同^[37]。优势木高反映了立地质量以及林分生长和收获，优势木高的参数估计值为正值，这表明由于立地质量的不同，优势木高与树高之间呈正相关关系，引入优势木高的广义模型更适用于树高−胸径模拟的拟合。

基于基础模型和各树种的最优广义模型，对应构建以样方水平为随机效应的混合模型，比较不同随机参数下各树种树高模型的拟合效果。研究发现，红松、紫椴和水曲柳基础混合效应模型均以增加随机参数 ${u}_{1}$ ，广义混合效应模型中红松增加参数 ${u}_{1}$ ，紫椴和水曲柳将 ${u}_{3}$ 同时作为随机参数，拟合效果最优；色木槭基础混合效应模型增加随机参数 ${u}_{1}$ 、 ${u}_{2}$ ，广义混合效应模型则是将 ${u}_{1}$ 、 ${u}_{3}$ 同时作为随机参数，预测精度最高。通过对各模型进行检验评价，结果表明混合效应模型对树高的预测效果优于固定效应模型，这与王冬至等^[38]的研究结果一致，表明考虑样方水平的随机影响能更好地描述树高生长规律。此外，本研究的模型评价和检验结果显示基础混合效应模型的预测能力略优于广义混合效应模型，但未有显著差异，同样的情况也出现在陈浩等^[39]对马尾松和周晏平等^[40]对樟子松的研究结果中，说明在增加样方效应后，林分变量对树高−胸径关系的影响被样方水平所涵盖，对混合效应模型的影响较弱。在Zang等^[41]对中国北部和东北落叶松人工林树高−胸径关系的研究中，基础混合效应模型比其他模型提供了更好的拟合和更稳定的估计，表明不需要额外的树木和林分变量。

4. 结　　论

本研究基于分位数回归和混合效应模型对阔叶红松林中优势树种红松、色木槭、紫椴和水曲柳的树高−胸径关系进行模型拟合，在11个非线性候选模型中确定Richards方程为基础模型，并引入优势木高构建广义模型，模型拟合结果得到较大提高；4个树种基于中位数回归的基础模型和广义模型拟合精度与基础模型的非线性回归相近。

加入样方水平为随机效应后，混合效应模型相较固定效应模型更具优越性，模型预测能力得到显著提高，而基础混合模型和广义混合模型的拟合优度差异较小。这表明林分变量和随机效应对树高模型的影响是显著的，在不考虑样方效应的情况下，可选择广义模型作为东北地区针阔混交林树高模型；若考虑样方效应，基础混合效应模型能提供更稳定的预测趋势和拟合结果。

图 1 低聚木聚糖标准品色谱图

X1代表木糖；X2代表木二糖；X3代表木三糖；X4代表木四糖；X5代表木五糖。

Figure 1. Chromatogram of xylo-oligosaccharide (XOS) standard

X1 represents xylose, X2 represents xylobiose, X3 represents xylotriose, X4 represents xylotetraose, and X5 represents xylopentaose.

下载: 全尺寸图片幻灯片

图 2 预处理前后甘蔗渣的接触角变化

Figure 2. Contact angles of untreated and pretreated sugarcane bagasse

下载: 全尺寸图片幻灯片

图 3 预处理前后甘蔗渣的X射线衍射谱图

Figure 3. X-ray diffraction spectra of untreated and pretreated sugarcane bagasse

下载: 全尺寸图片幻灯片

图 4 酶解时间对低聚木糖和木糖质量浓度的影响

Figure 4. Effects of time on the mass concentration of XOS and xylose

下载: 全尺寸图片幻灯片

图 5 预处理对低聚木糖初始生产速率的影响

Figure 5. Effects of pretreatment on the initial production rate of XOS

下载: 全尺寸图片幻灯片

图 6 预处理对低聚木糖生产的影响

Figure 6. Effects of pretreatments on XOS production

下载: 全尺寸图片幻灯片

表 1 NaOH-乙醇预处理甘蔗渣化学组成

Table 1 Chemical compositions of sugarcane bagasse pretreated by NaOH-ethanol

NaOH-乙醇预处理 NaOH-ethanol pretreatment	葡聚糖质量分数 Mass fraction of glucan	木聚糖质量分数 Mass fraction of xylan	木质素质量分数 Mass fraction of lignin	灰分质量分数 Mass fraction of ash	固体得率 Solid yield/%
未处理Untreated	(45.25±0.31)%	(23.30±0.30)%	(21.64±0.12)%	(1.94±0.04)%	100.00
5 g/L	(52.68±0.33)%	(26.31±0.24)%	(16.30±0.08)%	(1.20±0.06)%	84.30
10 g/L	(60.96±0.17)%	(27.50±0.18)%	(8.50±0.11)%	(0.91±0.08)%	71.67
15 g/L	(60.84±0.15)%	(28.62±0.09)%	(6.69±0.31)%	(1.09±0.03)%	70.85

下载: 导出CSV

参考文献(30)

[1]	Chen M H, Bowman M J, Dien B S, et al. Autohydrolysis of Miscanthus×giganteus for the production of xylooligosaccharides (XOS): kinetics, characterization and recovery[J]. Bioresource Technology, 2014, 155(2): 359-365.
[2]	Shin J H, Choi J H, Lee O S, et al. Thermostable xylanase from Streptomyces thermocyaneoviolaceus for optimal production of xylooligosaccharides[J]. Biotechnology and Bioprocess Engineering, 2009, 14(4): 391-399. doi: 10.1007/s12257-008-0220-3
[3]	石波, 李里特.低聚木糖的制备与分离[J].食品工业科技, 2004, 25(7): 113-114. doi: 10.3969/j.issn.1002-0306.2004.07.045 Shi B, Li L T. Study on the preparation and isolation of xylooligosacchrides[J]. Science and Technology of Food Industry, 2004, 25(7): 113-114. doi: 10.3969/j.issn.1002-0306.2004.07.045
[4]	Vallejos M E, Zambon M D, Area M C, et al. Low liquid-solid ratio (LSR) hot water pretreatment of sugarcane bagasse[J]. Green Chemistry, 2012, 14(7): 1982-1989. doi: 10.1039/c2gc35397k
[5]	Parajó J C, Garrote G, Cruz J M, et al. Production of xylooligosaccharides by autohydrolysis of lignocellulosic materials[J]. Trends in Food Science & Technology, 2004, 15(3-4): 115-120. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=Doaj000004160294
[6]	Saha B C. Hemicellulose bioconversion[J]. Journal of Industrial Microbiology and Biotechnology, 2003, 30(5): 279-291. doi: 10.1007/s10295-003-0049-x
[7]	Pérez J, Muñoz-Dorado J, de la Rubia T, et al. Biodegradation and biological treatments of cellulose, hemicellulose and lignin: an overview[J]. International Microbiology, 2002, 5(2): 53-63. doi: 10.1007/s10123-002-0062-3
[8]	Xue J L, Zhao S, Liang R M, et al. A biotechnological process efficiently co-produces two high value-added products, glucose and xylooligosaccharides, from sugarcane bagasse[J]. Bioresource Technology, 2016, 204: 130-138. doi: 10.1016/j.biortech.2015.12.082
[9]	顾阳, 勇强, 余世袁.高温预处理对木聚糖酶水解制备低聚木糖的促进作用[J].林产化学与工业, 2006, 26(1): 6-10. doi: 10.3321/j.issn:0253-2417.2006.01.002 Gu Y, Yong Q, Yu S Y. Promotional effect of high temperature pretreatment on enzymatic hydrolysis of xylan into xylooligosaccharide[J]. Chemistry and Industry of Forest Products, 2006, 26(1): 6-10. doi: 10.3321/j.issn:0253-2417.2006.01.002
[10]	Limayem A, Ricke S C. Lignocellulosic biomass for bioethanol production: current perspectives, potential issues and future prospects [J]. Progress in Energy and Combustion Science, 2012, 38(4): 449-467. doi: 10.1016/j.pecs.2012.03.002
[11]	秦书百川, 刘彦涛, 卜令习, 等.碱性亚硫酸盐耦合低压蒸汽预处理慈竹及其纤维素酶解转化[J].北京林业大学学报, 2016, 38(7): 98-104. doi: 10.13332/j.1000-1522.20150456 Qin S B C, Liu Y T, Bu L X, et al. Alkaline sulfite and low-pressure steam coupled pretreatment on Neosinocalamus affinis and its enzymatic hydrolysis[J]. Journal of Beijing Forestry University, 2016, 38(7): 98-104. doi: 10.13332/j.1000-1522.20150456
[12]	Sluiter A, Hames B, Ruiz R, et al. Determination of structural carbohydrates and lignin in biomass[R]//NREL. Technical report NREL/TP-510-42618. Golden, Colorado, USA: National Renewable Energy Laboratory, 2012.
[13]	Yu H L, You Y Z, Lei F H, et al. Comparative study of alkaline hydrogen peroxide and organosolv pretreatments of sugarcane bagasse to improve the overall sugar yield[J]. Bioresource Technology, 2015, 187: 161-166. doi: 10.1016/j.biortech.2015.03.123
[14]	杨淑娟, 游艳芝, 卜令习, 等.废纸脱墨浆预处理及其酶解性能研究[J].生物质化学工程, 2016, 50(4): 37-41. doi: 10.3969/j.issn.1673-5854.2016.04.007 Yang S J, You Y Z, Bu L X, et al. Pretreatment of waste paper pulp and enzymatic hydrolysis properties[J]. Biomass Chemical Engineering, 2016, 50(4): 37-41. doi: 10.3969/j.issn.1673-5854.2016.04.007
[15]	Aachary A A, Prapulla S G. Value addition to corncob: production and characterization of xylooligosaccharides from alkali pretreated lignin-saccharide complex using Aspergillus oryzae MTCC 5154[J]. Bioresource Technology, 2009, 100(2): 991-995. doi: 10.1016/j.biortech.2008.06.050
[16]	Morgan N K, Wallace A, Bedford M R, et al. Efficiency of xylanases from families 10 and 11 in production of xylo-oligosaccharides from wheat arabinoxylans[J]. Carbohydrate Polymers, 2017, 167: 290-296. doi: 10.1016/j.carbpol.2017.03.063
[17]	Azelee N I W, Jahim J M, Ismail A F, et al. High xylooligosaccharides (XOS) production from pretreated kenaf stem by enzyme mixture hydrolysis[J]. Industrial Crops and Products, 2016, 81: 11-19. doi: 10.1016/j.indcrop.2015.11.038
[18]	Si S L, Chen Y, Fan C F, et al. Lignin extraction distinctively enhances biomass enzymatic saccharification in hemicelluloses-rich Miscanthus species under various alkali and acid pretreatments[J]. Bioresource Technology, 2015, 183: 248-254. doi: 10.1016/j.biortech.2015.02.031
[19]	蒋建新, 杨中开, 朱莉伟, 等.竹纤维结构及其性能研究[J].北京林业大学学报, 2008, 30(1): 128-132. doi: 10.3321/j.issn:1000-1522.2008.01.023 Jiang J X, Yang Z K, Zhu L W, et al. Structure and property of bamboo fiber[J]. Journal of Beijing Forestry University, 2008, 30(1): 128-132. doi: 10.3321/j.issn:1000-1522.2008.01.023
[20]	徐勇, 陈牧, 余世袁, 等.木聚糖酶水解制取低聚木糖的研究[J].林产化学与工业, 2002, 22(2): 57-60. doi: 10.3321/j.issn:0253-2417.2002.02.014 Xu Y, Chen M, Yu S Y, et al. Study on enzymatic hydrolysis of xylan into xylo-oligosaccharide[J]. Chemistry and Industry of Forest Products, 2002, 22(2): 57-60. doi: 10.3321/j.issn:0253-2417.2002.02.014
[21]	蔡彦, 马玉龙, 谢丽, 等.不同预处理方法对麦草纤维素酶解效果的影响[J].可再生能源, 2010, 28(3): 72-74, 80. doi: 10.3969/j.issn.1671-5292.2010.03.016 Cai Y, Ma Y L, Xie L, et al. Comparative study on pretreatment of wheat straw cellulose with compound method[J]. Renewable Energy Resources, 2010, 28(3): 72-74, 80. doi: 10.3969/j.issn.1671-5292.2010.03.016
[22]	叶利培, 房桂干, 沈葵忠, 等.木聚糖酶水解竹材废弃物制取低聚木糖工艺条件的优化[J].食品工业科技, 2013, 34(22): 141-144, 148. http://d.old.wanfangdata.com.cn/Periodical/spgykj201322033 Ye L P, Fang G G, Shen K Z, et al. Optimization of xylo-oligosaccharides production by xylanase hydrolysis with bamboo wastes in processing[J]. Science and Technology of Food Industry, 2013, 34(22): 141-144, 148. http://d.old.wanfangdata.com.cn/Periodical/spgykj201322033
[23]	Yang S J, You Y Z, Li X L, et al. Effects of papermaking additives for effective hydrolysis of deinked waste paper[J]. Journal of Biobased Materials and Bioenergy, 2017, 11(2): 142-147. doi: 10.1166/jbmb.2017.1651
[24]	Reilly P J. Xylanases: structure and function[M]//Hollaender A, Rabson R, Rogers P, et al. Trends in the biology of fermentations for fuels and chemicals. Boston: Springer, 1981: 111-129.
[25]	Kumar S, Gupta R, Lee Y Y, et al. Cellulose pretreatment in subcritical water: effect of temperature on molecular structure and enzymatic reactivity[J]. Bioresource Technology, 2010, 101(4): 1337-1347. doi: 10.1016/j.biortech.2009.09.035
[26]	Yu H L, Tang Y, Xing Y, et al. Improvement of the enzymatic hydrolysis of furfural residues by pretreatment with combined green liquor and hydrogen peroxide[J]. Bioresource Technology, 2013, 147: 29-36. doi: 10.1016/j.biortech.2013.08.013
[27]	Zhao C, Ma Z Q, Shao Q J, et al. Enzymatic hydrolysis and physiochemical characterization of corn leaf after H-AFEX pretreatment[J]. Energy & Fuels, 2016, 30(2): 1154-1161. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=1e9e1185bfc0fcae841d56a9694a79d6
[28]	周玉恒, 陈海珊, 蔡爱华, 等.蒸汽爆破对甘蔗叶酶法制备低聚木糖的影响[J].食品与发酵工业, 2011, 37(2): 94-98. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=spyfx201102021 Zhou Y H, Chen H S, Cai A H, et al. The influence of steam explosion on enzymatic preparation of xylooligosaccharides from sugarcane leaves[J]. Food and Fermentation Industries, 2011, 37(2): 94-98. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=spyfx201102021
[29]	田龙, 王云, 马晓建.小麦秸秆酶法制备低聚木糖及其抗氧化活性[J].食品科学, 2014, 35(20): 88-92. doi: 10.7506/spkx1002-6630-201420018 Tian L, Wang Y, Ma X J. Preparation and antioxidant activity of xylooligosaccharides from wheat straw by enzymatic hydrolysis with xylanase[J]. Food Science, 2014, 35(20): 88-92. doi: 10.7506/spkx1002-6630-201420018
[30]	Jiang Z Q, Deng W, Zhu Y P, et al. The recombinant xylanase B of Thermotoga maritima is highly xylan specific and produces exclusively xylobiose from xylans, a unique character for industrial applications[J]. Journal of Molecular Catalysis B: Enzymatic, 2004, 27(4-6): 207-213. doi: 10.1016/j.molcatb.2003.11.012

施引文献(26)

期刊类型引用(13)

1.	陈仕媛，马岚，陈佩岩. 北方土石山区不同粒径团聚体特征及其对坡面侵蚀过程的影响. 水土保持研究. 2025(02): 102-110+139 . 百度学术
2.	张紫薇，赵文俊，李奇，马一淳，田亮，杨广勇，李忠武，刘窑军. 表层土壤结构对红壤坡耕地产流及产沙过程的影响. 土壤学报. 2024(02): 434-444 . 百度学术
3.	王琳涛，王云琦，王玉杰，张建聪，尹乐，张洪珊 . 火干扰对缙云山土壤团聚体稳定性的影响. 中国水土保持科学(中英文). 2023(03): 25-33 . 百度学术
4.	孙旭，马岚，张金阁，王福星，薛梦华，宋天翼，张旖璇，李浩玉. 模拟降雨条件下枯落物覆盖对坡面地表和壤中流产流过程的影响. 陕西师范大学学报(自然科学版). 2022(04): 136-144 . 百度学术
5.	刘文景，许文年，夏露，陈剑刚，程虎，余飞，夏栋，刘大翔，余绍鹏. 鄂西长江小流域土地利用方式对土壤团聚体稳定性的影响. 长江流域资源与环境. 2021(04): 925-935 . 百度学术
6.	郭岩松，毕曼. 土壤侵蚀影响因素研究进展. 河南科技. 2021(20): 136-140 . 百度学术
7.	黎俊佑，马岚，刘京晶，沈雨珺，张金阁，孙占薇，燕琳，张栋. 雨型对华北土石山区坡面土壤侵蚀的影响. 水土保持学报. 2020(04): 1-6 . 百度学术
8.	胡昭，张懿，郭建. 黄土丘陵区典型林地土壤团聚体稳定性评价. 人民黄河. 2020(08): 104-108 . 百度学术
9.	郭威震，胡斐南，谭滔滔，马任甜，刘婧芳，李喆，赵世伟. 土壤表面电场对黑土团聚体破碎和侵蚀的影响. 应用生态学报. 2020(08): 2644-2652 . 百度学术
10.	张金阁，马岚，张栋，刘京晶，黎俊佑，孙占薇，燕琳，孙旭，王福星. 华北土石山区草地过滤带布设方式对坡面产流产沙的影响. 水土保持学报. 2020(05): 76-80 . 百度学术
11.	毛旭芮，王明力，杨建军，丁肇龙，曹月娥. 采煤对露天煤矿土壤理化性质及可蚀性影响. 西南农业学报. 2020(11): 2537-2544 . 百度学术
12.	李肖，陈晨，林杰，朱茜，董波，丁鸣鸣. 侵蚀强度对淮北土石山区土壤团聚体组成及稳定性的影响. 水土保持研究. 2019(04): 56-61+67 . 百度学术
13.	王婷，李建平，张翼，井乐，张茹. 不同降水下天然草地土壤水稳定性团聚体分布特征. 草业科学. 2019(08): 1935-1943 . 百度学术

其他类型引用(13)

资源附件(0)

图(6) / 表(1)

计量

文章访问数: 2038
HTML全文浏览量: 467
PDF下载量: 64
被引次数: 26

1. 研究区概况与研究方法
1.1 研究区概况
1.2 数据来源与统计
1.3 研究方法
1.3.1 基础模型与广义模型
1.3.2 分位数回归
1.3.3 非线性混合效应模型
1.3.4 模型评价与检验
2. 结果与分析
2.1 基础模型拟合
2.2 广义模型构建
2.3 分位数回归
2.4 非线性混合效应模型构建
2.5 模型评价与检验
3. 讨　　论
3.1 基于基础模型的分位数回归
3.2 引入林分变量和随机效应对树高模型的影响
4. 结　　论

1. 研究区概况与研究方法
1.1 研究区概况
1.2 数据来源与统计
1.3 研究方法
1.3.1 基础模型与广义模型
1.3.2 分位数回归
1.3.3 非线性混合效应模型
1.3.4 模型评价与检验
2. 结果与分析
2.1 基础模型拟合
2.2 广义模型构建
2.3 分位数回归
2.4 非线性混合效应模型构建
2.5 模型评价与检验
3. 讨　　论
3.1 基于基础模型的分位数回归
3.2 引入林分变量和随机效应对树高模型的影响
4. 结　　论

参考文献(30)

施引文献(26)

资源附件(0)

NaOH-乙醇预处理提高甘蔗渣酶法制备低聚木糖效率

作者简介: 杨淑娟。主要研究方向：生物质能源及化学品。Email:yang2017bjfu@163.com 地址：100083北京市海淀区清华东路35号北京林业大学材料科学与技术学院

责任作者: 蒋建新，教授，博士生导师。主要研究方向：林产化工及生物质能源材料。Email: jiangjx@bjfu.edu.cn 地址：同上

计量

出版历程

NaOH-ethanol pretreatment increasing preparation efficiency of xylo-oligosaccharide from sugarcane bagasse with enzymatic hydrolysis

1. 研究区概况与研究方法

1.1 研究区概况

1.2 数据来源与统计

1.3 研究方法

1.3.1 基础模型与广义模型

1.3.2 分位数回归

1.3.3 非线性混合效应模型

1.3.4 模型评价与检验

2. 结果与分析

2.1 基础模型拟合

2.2 广义模型构建

2.3 分位数回归

2.4 非线性混合效应模型构建

2.5 模型评价与检验

3. 讨 论

3.1 基于基础模型的分位数回归

3.2 引入林分变量和随机效应对树高模型的影响

4. 结 论

期刊类型引用(13)

其他类型引用(13)

计量

出版历程

目录

1. 研究区概况与研究方法

1.1 研究区概况

1.2 数据来源与统计

1.3 研究方法

1.3.1 基础模型与广义模型

1.3.2 分位数回归

1.3.3 非线性混合效应模型

1.3.4 模型评价与检验

2. 结果与分析

2.1 基础模型拟合

2.2 广义模型构建

2.3 分位数回归

2.4 非线性混合效应模型构建

2.5 模型评价与检验

3. 讨 论

3.1 基于基础模型的分位数回归

3.2 引入林分变量和随机效应对树高模型的影响

4. 结 论

作者简介:
杨淑娟。主要研究方向：生物质能源及化学品。Email:yang2017bjfu@163.com 地址：100083北京市海淀区清华东路35号北京林业大学材料科学与技术学院

责任作者:
蒋建新，教授，博士生导师。主要研究方向：林产化工及生物质能源材料。Email: jiangjx@bjfu.edu.cn 地址：同上

3. 讨　　论

4. 结　　论

3. 讨　　论

4. 结　　论