基于联立方程组的人工樟子松枝下高模型构建

李想; 董利虎; 李凤日

doi:10.13332/j.1000-1522.20170428

基于联立方程组的人工樟子松枝下高模型构建

东北林业大学林学院，黑龙江哈尔滨 150040

基金项目:

国家自然科学基金项目 31570626

详细信息

作者简介:
李想。主要研究方向：林分生长模型。Email：lx0326999@163.com 地址：150040 黑龙江省哈尔滨市香坊区和兴路26号东北林业大学林学院

责任作者:
李凤日，教授。主要研究方向：林分生长模型。Email：fengrili@126.com 地址：同上

中图分类号: S758.5
计量
- 文章访问数: 1930
- HTML全文浏览量: 490
- PDF下载量: 34
出版历程
- 收稿日期: 2017-11-28
- 修回日期: 2018-04-16
- 发布日期: 2018-05-31

Building height to crown base models for Mongolian pine plantation based on simultaneous equations in Heilongjiang Province of northeastern China

School of Forestry, Northeast Forestry University, Harbin 150040, Heilongjiang, China

摘要

摘要:
目的基于黑龙江省帽儿山实验林场、横头山林场、孟家岗林场的61块樟子松人工林固定样地的5211株样木调查数据，构建了树高模型与枝下高模型的联立方程组。
方法首先，从8种常用的标准树高曲线，选出拟合效果较好的2个模型作为树高曲线的备选模型。再以5个枝下高预估模型作为基础模型，通过引入林木及林分变量(林木大小，竞争因子，立地条件)采用最优子集回归法筛选出3个变量少且拟合效果较好的模型作为枝下高备选模型。将树高曲线备选模型与枝下高备选模型分别两两联立，建立树高与枝下高联立方程组模型，采用似乎不相关回归(SUR)对模型参数进行求解。最后，对联立方程组进行评价。
结果树高(H)和枝下高(HCB)与林分断面积(G)和优势木平均高(H₀)呈正相关。最优的联立方程组预估树高时调整后相关系数(R_a²)为0.9520，均方根误差(RMSE)为1.17m；预估枝下高时的R_a²为0.9066，RMSE为1.36m，并且模型的各项检验指标数值较小。
结论整体来看，联立方程组的拟合效果较好，预估精度较高，同时联立方程组解决了树高与枝下高的内在相关性问题。本文所建立的含林分因子的树高模型与枝下高模型联立方程组可以很好地预估不同林分条件下樟子松人工林的树高和枝下高，为进一步研究樟子松树冠结构和动态提供了基础。
- 樟子松人工林 /
- 树高曲线 /
- 枝下高 /
- 似乎不相关回归 /
- 联立方程组
Abstract:
ObjectiveBased on the data of 5211 sample trees in 61 permanent sample plots in Mongolian pine plantations from Maoershan Experimental Forest Farm, Hengtoushan Forest Farm, Mengjiagang Forest Farm in Heilongjiang Province of northeastern China, the simultaneous equations for tree height model and height to crown base model were developed.
MethodAt first, 2 alternative height-diameter models had been selected by comparing the goodness of fit for 8 height-diameter models. From 5 basic height to crown base(HCB)models, 3 best HCB models including tree and stand variables (tree size, competition index, site condition) were selected as alternative models using the method of all subset regression. Based on the seeming unrelated regression (SUR), the parameters of the simultaneous equations model of height and HCB were estimated considering each kind of combinations for 2 alternative height-diameter models and 3 alternative HCB models, respectively. Finally, we evaluated the fitting effect of the simultaneous equation model.
ResultThe results showed that H and HCB were positively correlated with basal area (G) and average height of dominant tree (H₀). For the best simultaneous equations, the coefficient determination (R_a²) was 0.9520 and the root-mean-square error (RMSE) was 1.17m by fitting height (H), the R_a² was 0.9066, and RMSE was 1.36m by fitting HCB. The validation values of the best simultaneous equations were smaller.
ConclusionOn the whole, the simultaneous equations developed performed well in predicting the tree H and HCB simultaneously with the least predicting errors, and the model could handle correlations between tree H and HCB. The simultaneous equations considering stand variables developed in this paper could be suitable for predicting H and HCB for Mongolian pine plantations with different stand conditions and it will provide basis for future research on the crown structure and dynamics.
- Mongolian pine (Pinus sylvestris var. mogolica) plantation /
- tree height curve /
- height to crown base /
- seeming unrelated regression (SUR) /
- simultaneous equations

HTML全文

图 1 联立方程组的树高预估值及枝下高预估值的残差分布

Figure 1. Residual distribution of predicted H and HCB of simultaneous equation model

下载: 全尺寸图片幻灯片

图 2 其他条件相同时(D₀=22.6cm, H₀=16m)不同竞争条件下树高和枝下高分别与胸径的关系曲线

Figure 2. Relationship between H and HCB with DBH considering D₀=22.6cm and H₀=16m for differentG

下载: 全尺寸图片幻灯片

图 3 其他条件相同时(D₀=22.6cm, G=33m²)不同立地条件下树高和枝下高分别与胸径的关系曲线

Figure 3. Relationship between H and HCB with DBH considering D₀=22.6cm and G=33m² for different H₀

下载: 全尺寸图片幻灯片

图 4 模型(7)和模型(25)拟合不同径阶树高的平均误差

Figure 4. ME obtained for diameter classes in the fitting H of model (7) and model (25)

下载: 全尺寸图片幻灯片

图 5 模型(22)和模型(25)拟合不同径阶树的枝下高的平均误差

Figure 5. ME obtained for diameter classes in the fitting HCB of model (22) and model (25)

下载: 全尺寸图片幻灯片

表 1 樟子松人工林样木及林分因子特征表

Table 1 Summary statistics of stand sample tree variables for Mongolian pine plantation

变量 Variable	平均值 Mean	最大值 Max.	最小值 Min.	标准差 S.D.
胸径Diameter at breast height (DBH)/cm	15.3	39.2	3.3	6.2
树高Tree height (H)/m	13.3	25.4	3.0	5.3
枝下高Height to crown base (HCB)/m	8.5	19.8	0.1	4.4
林分平均胸径Average stand DBH (D_g)/cm	18.3	33.4	6.3	6.5
林分平均高Mean stand height (H_m)/m	15.6	25.2	4.3	6.0
林分断面积/(m²·hm^-2) Stand basal area (G)/(m²·ha^-1)	33.1	48.0	9.6	8.2
大于对象木的断面积和/(m²·hm^-2) Basal area sum larger than subject tree (BAL)/(m ²·ha ^-1)	20.3	47.7	0.0	10.8
优势木平均胸径Mean DBH of dominant tree (D₀)/cm	23.0	10.0	9.4	6.0
优势木平均高Mean tree height of dominant tree (H₀)/m	16.0	24.7	5.2	5.2
年龄Stand age (A)/a	33	48	12	11.3
林分密度/(株·hm^-2) Stand density (SD)/(tree·ha^-1)	1 921	4 800	385	1 020.6

下载: 导出CSV

表 2 8种树高曲线模型

Table 2 8 tree height-diameter functions

模型编号 Model No.	表达式 Expression	参考文献 Reference
(1)	$H=1.3+a_{0} G^{a_{1}}\left(1-e^{-a_{2} \times D B H}\right)$	[21]
(2)	$H=1.3+\left[a_{0}\left(\frac{1}{\mathrm{DBH}}-\frac{1}{D_{0}}\right)+\left(\frac{1}{H_{0}-1.3}\right)^{\frac{1}{3}}\right]^{-3}$	[22]
(3)	$H=1.3+\left(H_{0}-1.3\right)\left(\frac{\mathrm{DBH}}{D_{0}}\right)^{a_{0}}$	[23]
(4)	$H=1.3+\left(H_{0}-1.3\right) \frac{1-\mathrm{e}^{a_{0} \times \mathrm{DBH}}}{1-\mathrm{e}^{a_{0} D_{0}}}$	[23]
(5)	$H=1.3+\left(H_{0}-1.3\right) \mathrm{e}^{a_{0}\left(1-\frac{D_{\mathrm{g}}}{\mathrm{DBH}}\right.} )+a_{1}\left(\frac{1}{D_{\mathrm{g}}}-\frac{1}{\mathrm{DBH}}\right)$	[23]
(6)	$H=1.3+\left(H_{\mathrm{m}}-1.3\right) \mathrm{e}^{a_{0}\left(1-\frac{\mathrm{DBH}}{D_{\mathrm{g}}}\right.} )+a_{1}\left(\frac{\mathrm{DBH}}{D_{\mathrm{g}}}-\frac{1}{\mathrm{DBH}}\right)$	[23]
(7)	$H=1.3+\left(a_{0}+a_{1} H_{0}-a_{2} D_{\mathrm{g}}+a_{3} G\right) \mathrm{e}^{-a_{4} / \sqrt{\mathrm{DBH}}}$	[24]
(8)	$H=1.3+\left(a_{0}+a_{1} \times \mathrm{BAL}\right) \exp \left(-a_{2} / \mathrm{DBH}\right)$	[25]
注：a₀、a₁、a₂、a₃、a₄为模型参数。Notes:a₀, a₁, a₂, a₃, a₄ refer to model parameters.

下载: 导出CSV

表 3 枝下高预估模型的基础形式

Table 3 Basic forms of predicting models for height to crown base

模型编号 Model No.	表达式 Expression	模型形式 Model form	因变量的范围 Range of dependent variable	参考文献 Reference
(9)	HCB=H(1.0－expX)	指数形式Exponential form	(-∞, H)	[10]
(10)	HCB=H(1.0－expX²)	指数形式Exponential form	(-∞, H)	[11]
(11)	HCB=H(1.0－c×expX^w)	指数形式Exponential form	(-∞, H)	[17]
(12)	HCB=H/(1.0+expX)	Logistic形式Logistic form	(0, H)	[11]
(13)	HCB=H/(1.0+c×exp X)^1/m	Logistic形式Logistic form	(0, H)	[17]
注：c、m、w为模型参数；X为关于林木大小、竞争因子、立地条件的函数。Notes:c, m and w refer to model parameters；X is the function about tree size competition index and site condition.

下载: 导出CSV

表 4 树高曲线模型的参数估计值、拟合优度及检验结果

Table 4 Results of parameter estimates, goodness of fit and validation result of height-diameter models

模型编号 Model No.	参数 Parameter	参数估计值 Parameter estimate	标准误 Standard error	拟合优度 Goodness of fitting		检验结果 Validation result
模型编号 Model No.	参数 Parameter	参数估计值 Parameter estimate	标准误 Standard error	R_a²	RMSE/m	ME/m	MAE/m	TRE/%	MPE/%
(2)	a₀	1.0622	0.00955	0.9438	1.26	0.32	0.99	-2.19	6.42
(3)	a₀	0.4441	0.00370	0.9440	1.26	0.27	1.00	-1.94	6.39
(4)	a₀	-0.0769	0.000765	0.9441	1.26	0.20	0.99	-1.58	6.43
(6)	a₀	-0.0162	0.00656	0.9453	1.24	-0.08	0.95	-1.26	6.18
(6)	a₁	-0.1337	0.00552	0.9453	1.24	-0.08	0.95	-1.26	6.18
(7)	a₀	3.0443	1.3120	0.9520	1.17	-0.00	0.89	-0.43	5.90
	a₁	1.3103	0.0138
	a₂	2.6453	0.8350
	a₃	0.1984	0.0431
	a₄	2.3579	0.0493

下载: 导出CSV

表 5 枝下高基础模型的参数估计值、拟合优度及检验结果

Table 5 Results of parameter estimates, goodness of fit and validations of basic height to crown base models

模型编号 Model No.	参数 Parameter	参数估计值 Parameter estimate	标准误 Standard error	拟合优度 Goodness of fitting		检验结果 Validation result
模型编号 Model No.	参数 Parameter	参数估计值 Parameter estimate	标准误 Standard error	R_a²	RMSE/m	ME/m	MAE/m	TRE/%	MPE/%
(9)	b₀	-0.877 7	0.018 3	0.8579	1.68	-0.28	1.45	-3.37	14.59
(9)	b₁	-0.0105	0.00865	0.8579	1.68	-0.28	1.45	-3.37	14.59
(10)	b₀	-0.978 8	0.010 8	0.856 8	1.69	-0.31	1.45	-3.72	14.52
(10)	b₁	-0.000273	0.000126	0.856 8	1.69	-0.31	1.45	-3.72	14.52
(11)	b₀	-0.978 8	0.011 4	0.856 8	1.69	-0.31	1.45	-3.72	14.52
(11)	b₁	-0.000 336	0.000 135	0.856 8	1.69	-0.31	1.45	-3.72	14.52
(12)	b₀	-0.3623	0.0287	0.8578	1.68	-0.28	1.45	-3.36	14.58
(12)	b₁	-0.015 6	0.001 51	0.8578	1.68	-0.28	1.45	-3.36	14.58
(13)	b₀	3.061 5	0.066 2	0.857 6	1.68	-0.28	1.45	-3.36	14.58
(13)	b₁	-0.0337	0.00332	0.857 6	1.68	-0.28	1.45	-3.36	14.58

下载: 导出CSV

表 6 枝下高备选模型的拟合优度及检验结果

Table 6 Results of goodness of fitting and validations of height to crown base candidate models

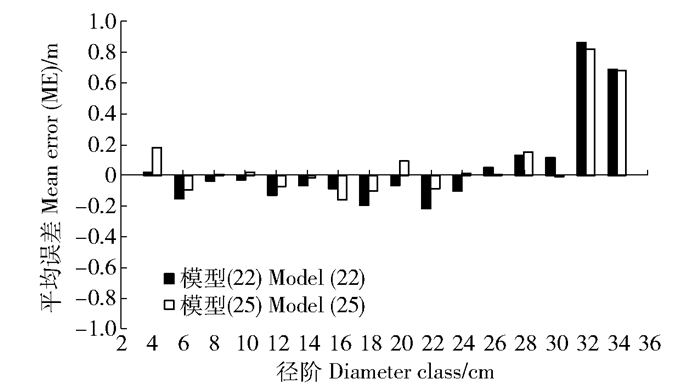
模型编号 Model No.	表达式 Expression	拟合优度 Goodness of fitting		检验结果 Validation result
模型编号 Model No.	表达式 Expression	R_a²	RMSE/m	ME/m	MAE/m	TRE/%	MPE/%
(22)	HCB=H/(1+exp(b+c×DBH+dG+eH₀))	0.906 7	1.32	-0.01	1.01	-0.15	11.07
(23)	HCB=H/(1+exp(b+c×DBH+d×BAL+eH₀))	0.905 3	1.33	-0.01	1.02	-0.09	11.17
(24)	HCB=H/(1+exp(b+c×DBH+d×HDR+eH₀))	0.904 1	1.34	-0.01	1.03	-0.10	11.22

下载: 导出CSV

表 7 联立方程组(25)的参数估计结果

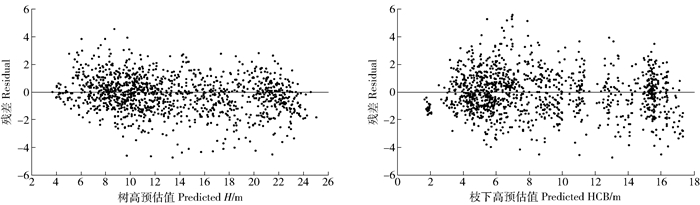
Table 7 Results of parameter estimates for simultaneous equations model (25)

参数 Parameter	参数估计值 Parameter estimate	树高 Tree height (H)						枝下高 Height to crown base (HCB)
		拟合优度 Goodness of fitting		检验结果 Validation result				拟合优度 Goodness of fitting		检验结果 Validation result
		R_a²	RMSE/m	ME/m	MAE/m	TRE/%	MPE/%	R_a²	RMSE/m	ME/m	MAE/m	TRE/%	MPE/%
a₀	2.1629	0.9520	1.17	-0.00	0.89	1.67	6.34	0.906 6	1.36	0.02	1.01	-0.26	11.07
a₁	1.310 7
a₂	2.111 6
a₃	0.171 3
a₄	2.348 9
b	0.554 0
c	0.038 7
d	-0.015 2
e	-0.070 6

下载: 导出CSV

参考文献(36)

[1]	Sharma R P, Vacek Z, Vacek S, et al. Modelling individual tree height to crown base of Norway spruce (Picea abies (L.) Karst.) and European beech (Fagus sylvatica L.)[J/OL]. Plos One, 2017, 12(10): e0186394[2017-09-09].https://doi.org/10.1371/journal.pone.0186394.
[2]	Pearcy R W, Muraoka H, Valladares F. Crown architecture in sun and shade environments: assessing function and trade-offs with a three-dimensional simulation model[J].New Phytologist, 2005, 166(3):791-800. doi: 10.1111/j.1469-8137.2005.01328.x
[3]	卢军, 李凤日, 张会儒, 等.帽儿山天然次生林主要树种冠长率模型[J].林业科学, 2011, 47(6):70-76. http://d.old.wanfangdata.com.cn/Periodical/lykx201106011 Lu J, Li F R, Zhang H R, et al. A crown ratio model for dominant species in secondary forests in Mao'er Mountain[J]. Scientia Silvae Sinicae, 2011, 47(6):70-76. http://d.old.wanfangdata.com.cn/Periodical/lykx201106011
[4]	Kuprevicius A, Auty D, Achim A, et al. Quantifying the influence of live crown ratio on the mechanical properties of clear wood[J]. Forestry, 2013, 86(3):361-369. doi: 10.1093/forestry/cpt006
[5]	苏乙奇.人工落叶松枝下高动态研究[J].林业调查规划, 2008, 33(1):21-24. doi: 10.3969/j.issn.1671-3168.2008.01.007 Su Y Q. Dynamic study on under branch height of artificial Larix gmelinii[J]. Forest Inventory & Planning, 2008, 33(1): 21-24. doi: 10.3969/j.issn.1671-3168.2008.01.007
[6]	Temesgen H, Lemay V, Mitchell S J. Tree crown ratio models for multi-species and multi-layered stands of southeastern British Columbia[J]. Forestry Chronicle, 2005, 81(1):133-141. doi: 10.5558/tfc81133-1
[7]	Rijal B, Weiskittel A R, Kershaw J A J. Development of height to crown base models for thirteen tree species of the North American Acadian Region[J]. Forestry Chronicle, 2012, 88(1): 60-73. doi: 10.5558/tfc2012-011
[8]	Fu L, Zhang H, Sharma R P, et al. A generalized nonlinear mixed-effects height to crown base model for Mongolian oak in northeast China[J]. Forest Ecology & Management, 2017, 384(1):34-43. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=83c472951bb41ee708d7b0744b17a432
[9]	陈东升, 孙晓梅, 李凤日, 等.落叶松人工林节子内部特征变化规律研究[J].北京林业大学学报, 2015, 37(2):16-23. doi: 10.13332/j.cnki.jbfu.2015.02.014 Chen D S, Sun X M, Li F R, et al. Changes of the internal characteristics of knots in larch plantation[J]. Journal of Beijing Forestry University, 2015, 37(2):16-23. doi: 10.13332/j.cnki.jbfu.2015.02.014
[10]	Wykoff W R, Crookston N L, Stage A R. User's guide to the stand prognosis model[R]. USDA Forest Service, United States Department of Agriculture, 1982.
[11]	Walters D K, Hann D W. Taper equations for six conifer species in southwest Oregon[M]. Corvallis: Oregon State University, 1986.
[12]	Hanus M L, Hann D W, Marshall D D. Predicting height to crown base for undamaged and damaged trees in southwest Oregon[M]. Corvallis: Oregon Stage University, 2000.
[13]	Hann D W, Marshall D D, Hanus M L. Equations for predicting height-to-crown-base, 5-year diameter growth rate, 5-year height growth rate, 5-year mortality rate and maximum size-density trajectory for Douglas-fir and western hemlock in the coastal region of the Pacific Northwest[M]. Corvallis: Oregon Stage University, 2003.
[14]	赵俊卉, 亢新刚, 刘燕.长白山主要针叶树种最优树高曲线研究[J].北京林业大学学报, 2009, 31(4):13-18. doi: 10.3321/j.issn:1000-1522.2009.04.003 Zhao J H, Kang X G, Liu Y. Optimal height-diameter models for dominant coniferous species in Changbai Mountain, northeastern China[J]. Journal of Beijing Forestry University, 2009, 31(4):13-18. doi: 10.3321/j.issn:1000-1522.2009.04.003
[15]	卢军, 张会儒, 雷相东, 等.长白山云冷杉针阔混交林幼树树高-胸径模型[J].北京林业大学学报, 2015, 37(11):10-25. doi: 10.13332/j.1000-1522.20140429 Lu J, Zhang H R, Lei X D, et al. Height-diameter models for saplings in a spruce-fir mixed forest in Changbai Mountains[J]. Journal of Beijing Forestry University, 2015, 37(11):10-25. doi: 10.13332/j.1000-1522.20140429
[16]	王冬至, 张冬燕, 王方, 等.塞罕坝主要立地类型针阔混交林树高曲线构建[J].北京林业大学学报, 2016, 38(10):7-14. doi: 10.13332/j.1000-1522.20150359 Wang D Z, Zhang D Y, Wang F, et al. Height curve construction of needle and broadleaved mixed forest under main site types in Saihanba, Hebei of northern China[J]. Journal of Beijing Forestry University, 2016, 38(10):7-14. doi: 10.13332/j.1000-1522.20150359
[17]	Kershaw J A J, Maguire D A, Hann D W. Longevity and duration of radial growth in Douglas-fir branches[J]. Canadian Journal of Forest Research, 1990, 20(11):1690-1695. doi: 10.1139/x90-225
[18]	Russell M B, Weiskittel A R, Kershaw J A. Comparing strategies for modeling individual-tree height and height-to-crown base increment in mixed-species Acadian forests of northeastern North America[J]. European Journal of Forest Research, 2014, 133(6):1121-1135. doi: 10.1007/s10342-014-0827-1
[19]	Dong L, Zhang L, Li F. A three-step proportional weighting system of nonlinear biomass equations[J]. Forest Science, 2015, 61(1): 35-45. doi: 10.5849/forsci.13-193
[20]	Sibbesen E. Some new equations to describe phosphate sorption by soils[J]. European Journal of Soil Science, 2010, 32(1):67-74. http://cn.bing.com/academic/profile?id=8073e9be9f6ab4cd3d0fec82d0ef58e4&encoded=0&v=paper_preview&mkt=zh-cn
[21]	Sharma M, Zhang S Y. Height-diameter models using stand characteristics for Pinus banksiana and Picea mariana[J]. Scandinavian Journal of Forest Research, 2004, 19(5):442-451. doi: 10.1080/02827580410030163
[22]	Mønness E. Diameter distributions and height curves in even-aged stands of Pinus sylvestris L.[J]. Norsk Institutt for Skogforskning, 1982, 36(15):1-40.
[23]	Sánchez C A L, Varela J G, Dorado F C, et al. A height-diameter model for Pinus radiata D. Don in Galicia (Northwest Spain)[J]. Annals of Forest Science, 2003, 60(3):237-245. doi: 10.1051/forest:2003015
[24]	Schröder J, González J G Á. Comparing the performance of generalized diameter-height equations for Maritime pine in Northwestern Spain[J]. Forstwissenschaftliches Centralblatt vereinigt mit Tharandter forstliches Jahrbuch, 2001, 120(1-6):18-23. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=27925fc274150a0d9c08098af3d5c270
[25]	Adame P, Río M D, Cañellas I. A mixed nonlinear height-diameter model for pyrenean oak (Quercus pyrenaica Willd.)[J]. Forest Ecology & Management, 2008, 256(1):88-98. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=64d92a26a96433943f26c1080521b0fc
[26]	Li F. Modeling crown profile of Larix olgensis trees[J]. Scientia Silvae Sinicae, 2004, 40(5):16-24. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=lykx200405003
[27]	曾伟生, 唐守正.立木生物量方程的优度评价和精度分析[J].林业科学, 2011, 47(11):106-113. doi: 10.11707/j.1001-7488.20111117 Zeng W S, Tang S Z. Goodness evaluation and precision analysis of tree biomass equations[J]. Scientia Silvae Sinicae, 2011, 47(11):106-113. doi: 10.11707/j.1001-7488.20111117
[28]	Soares P, Tomé M. A tree crown ratio prediction equation for eucalypt plantations[J]. Annals of Forest Science, 2001, 58(2):193-202. doi: 10.1051/forest:2001118
[29]	胥辉, 全宏波, 王斌.思茅松标准树高曲线的研究[J].西南林业大学学报, 2000, 20(2):74-77. http://d.old.wanfangdata.com.cn/Periodical/xnlxyxb200002003 Xu H, Quan H B, Wang B. Study on standard diameter-height curves model of Pinus kesiya var. langbianensis[J]. Journal of Southwest Forestry College, 2000, 20(2): 74-77. http://d.old.wanfangdata.com.cn/Periodical/xnlxyxb200002003
[30]	马武, 雷相东, 徐光, 等.蒙古栎天然林单木生长模型的研究(Ⅱ):树高—胸径模型[J].西北农林科技大学学报(自然科学版), 2015, 43(3):83-90. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xbnydxxb201503012 Ma W, Lei X D, Xu G, et al. Growth model for individual-tree in natural Quercus mongolica forests (Ⅱ): height-diameter model[J]. Journal of Northwest A&F University (Natural Science Edition), 2015, 43(3): 83-90. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xbnydxxb201503012
[31]	Sonmez T. Generalized height-diameter models for Picea orientalis L.[J]. Journal of Environmental Biology, 2009, 30(5):767-772. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=Open J-Gate000001038151
[32]	董云飞, 孙玉军, 许昊. 3种标准树高曲线建立方法的比较[J].西北农林科技大学学报(自然科学版), 2015, 43(11):82-90. http://d.old.wanfangdata.com.cn/Periodical/xbnydxxb201511012 Dong Y F, Sun Y J, Xu H. Comparison of three methods for constructing generalized height-diameter curve[J]. Journal of Northwest A& University (Natural Science Edition), 2015, 43(11): 82-90. http://d.old.wanfangdata.com.cn/Periodical/xbnydxxb201511012
[33]	段文标, 王春萍.樟子松人工林生长与立地因子间关系的研究:草牧场防护林主要适地适树初步研究[J].东北林业大学学报, 1994, 22(5):1-6. http://www.cqvip.com/Main/Detail.aspx?id=1321485 Duan W B, Wang C P. Study on the relationship between growth and site factors of Mongolian Scots pine: a preliminary study on the main species in the shelter forest of grassland[J]. Journal of Northeast Forestry University, 1994, 22(5): 1-6. http://www.cqvip.com/Main/Detail.aspx?id=1321485
[34]	罗玲.榆林沙区不同立地条件下樟子松人工林生长规律的研究[D].杨凌: 西北农林科技大学, 2008. Luo L. Research on growth characteristics of Mongolian Pine on different sites in Yulin sandland area[D]. Yangling: Northwest A& University, 2008.
[35]	贾炜玮.樟子松人工林枝条生长及节子大小预测模型的研究[D].哈尔滨: 东北林业大学, 2006. Jia W W. Predicting models of branch growth and knot properties for Mongolian Scots pine in plantation[D]. Harbin: Northeast Forestry University, 2006.
[36]	孙鸿宇, 宋丁全, 王福生.不同立地条件对毛竹枝下高的影响研究[J].金陵科技学院学报, 2009, 8(4):61-65. doi: 10.3969/j.issn.1672-755X.2009.04.016 Sun H Y, Song D Q, Wang F S. Effects of different site conditions on under-branch height of Phyllostachys pubescens Mazel[J]. Journal of Jinling Institute of Technology, 2009, 8(4):61-65. doi: 10.3969/j.issn.1672-755X.2009.04.016

施引文献(6)

期刊类型引用(4)

1.	张苗苗，罗于洋，王树森，张丽娜，马成功，于胜利，王景圆. 内蒙古旺业甸华北落叶松人工林空间结构分析及其优化. 西北林学院学报. 2024(01): 81-87+107 . 百度学术
2.	荆媛，魏爽，史文辉，马梓贺，王德宇，戎可. 天然次生林中小斑啄木鸟的取食偏好. 野生动物学报. 2024(01): 84-94 . 百度学术
3.	孙宇，刘盛，田佳歆，程福山，赵士博，王诗俊. 基于空间结构优化的长白落叶松人工林分间伐模型构建. 中南林业科技大学学报. 2023(01): 72-83 . 百度学术
4.	刘鑫，黄浪，卿东升，李建军. 基于Voronoi空间单元的林分空间结构智能优化研究. 林业资源管理. 2023(04): 27-35 . 百度学术