Evaluating stand growth state by potential density of stocking
-
摘要:目的林分长势是林分活力的直接体现，疏密度是反映林分密度和长势的重要指标之一。计算疏密度的关键是对标准断面积的准确求算，但在实际应用中标准林分难以判定，标准断面积的可获得性较差，削弱了其可应用性，探求新的指标是解决这一问题的有效途径，因此本研究旨在探究可以替代疏密度的新指标。方法一定的立地条件下，林地生产力是有限的，基于最终产量恒定法则，本研究以长期连续监测且经营数表齐全的杉木试验林分为材料，1989年编制的全国分区杉木标准表为参照，以林分内不同比例较大林木个体的平均断面积与全部林木株数的乘积表示林分生长能够达到的潜在最大断面积，即在50% ~ 80%林木株数比例范围内，以5%为梯度，依次比较不同比例较大林木个体所得潜在最大断面积与标准断面积的差值，求使潜在最大断面积与标准断面积偏差率最小时所对应林木株数比例，并以此为基础，分析天然林中林分断面积与潜在最大断面积的关系，检验潜在最大断面积的计算方法在天然林中的适用性。结果当较大林木株数占总株数比例为70%时，所有试验样地的潜在最大断面积与标准断面积的偏差最小，均在 ± 10%左右，此时，潜在疏密度与疏密度的差值最小；天然林中70%较大林木个体断面积之和与林分断面积呈显著线性关系，故可用70%较大个体的平均断面积与总株数乘积作为潜在最大断面积，来求算潜在疏密度。结论林分潜在最大断面积可以70%较大林木个体平均断面积与林木总株数的乘积表示，所求潜在疏密度可替代疏密度来表征林分长势。Abstract:ObjectiveStand growth is a direct reflection of stand vitality, density of stocking is one of the most commonly used indices to reflect the degree of closeness and its growth status in a stand. Accurate calculation of standard basal area is the key to calculate density of stocking, but it has poor availability and applicability because of the difficulty to distinguish standard stand among all stands of an area. exploring an alternative index is an effective way to solve this problem. Therefore, the purpose of this study is to find the new index.MethodThe potential productivity of a forest is finite under certain site conditions. Based on the Law of Constant Ultimate Capacity, in this study, we analyzed Cunninghamia lanceolata plantations under continuous monitoring with its growth process data all in readiness, with Cunninghamia lanceolata standard tables, which compiled in 1989 as cross reference. The potential maximum basal area of the stand was expressed by the product of the average basal area of a certain percentage of larger individuals and the total number of trees in the stand. Comparing the proportion from 50%−80% at 5% interval, we seek to find the ratio when the deviation rate between the potential maximum basal area and standard basal area was at its minimal value, and analyzed the applicability of potential maximum basal area in natural forests on this basis.Resultthe results suggested when the proportion was 70%, the deviation rate between the potential maximum basal area and the standard basal area of all test plots was about ± 10%, and the difference between the potential density of stocking and the density of stocking was at its minimal value. Furthermore, in order to test the applicability to natural forests, statistical analysis indicated that there was a significant linear relationship between the basal area with 70% as the larger trees and the stand basal area in the natural forest. The results showed that the potential density of stocking of a stand could be calculated by the product of the average basal area with 70% as the larger trees and the total number of trees.ConclusionThe potential maximum stand basal area could be expressed as the product of the average basal area with 70% as the larger trees and the total number of trees. The potential density of stocking, as an alternative index, can replace the density of stocking to characterize density and growth status of a stand.
-
盐胁迫是影响植物生长发育的不利环境因子。面对盐胁迫，植物通过体表盐腺、叶片肉质化、渗透调节、离子区隔化等方式，降低体内钠离子（Na+）水平，排出体内过量的Na + [1−3]。另一方面，植物通过活性氧（ROS）、钙离子（Ca2+）、胞外ATP（eATP）、硫化氢（H2S）、一氧化氮（NO）等信号调节分子，激活植物体内的抗氧化物酶系统及相应的耐盐分子调控通路[4−8]。
在分子水平上，植物的耐盐性是由多个基因决定的[9]。盐胁迫下，不同种类的抗逆基因编码的蛋白质，通过参与各种生理代谢过程，构建了植物耐盐的调控网络[10]。其中蛋白激酶在植物响应盐胁迫的信号转导过程中发挥了重要作用。植物促分裂原活化蛋白激酶（mitogen activated protein kinase，MAPK）级联途径能被干旱、高盐、低温等多种胁迫信号激活[11−12]。Wang等[13]在水稻（Oryza sativa）中发现：OsMKK1和OsMPK4共同构成调控水稻响应盐胁迫的一个信号通路。植物类受体蛋白激酶（receptor-like protein kinases，RLKs）通过配体结合区感应胁迫信号，经跨膜磷酸基团传递，进行信号转导[14]。Zhou等[15]鉴定得到水稻耐盐基因STRK1，并证明了该基因提高水稻耐盐性的分子机制是由RLKs磷酸化过程调控的。Miyata等[16]发现：在拟南芥（Arabidopsis thaliana）中过表达类受体蛋白激酶基因OsRLK2可降低拟南芥的耐盐性。钙依赖蛋白激酶（calcium-dependent protein kinase，CDPK）是一类丝氨酸/苏氨酸蛋白激酶，作为Ca2+信号感受器参与了多种逆境信号通路[17−19]。Asano等[20]发现：OsCPK12参与激素的信号转导，并对水稻抗逆性有正调控作用。
SOS2-LIKE蛋白激酶5（salt overly sensitive 2-like protein kinase 5，PKS5），也称为CBL互作蛋白（CIPK11）、SNF1相关蛋白激酶3型蛋白激酶（SNRK3.22），是CBLs相互作用蛋白激酶家族成员之一，是盐超敏感信号通路（salt overly sensitive，SOS）中非常重要的调控因子[21−22]。PKS5不仅参与植物盐胁迫信号传递，也参与响应其他非生物胁迫[23−25]。PKS5在拟南芥对镉的耐受性中起正向调控作用，但是过表达PKS5降低了拟南芥对干旱胁迫和碱胁迫的抗性[26−28]。同时PKS5通过磷酸化ABI5、MYB、NAC和ERF等转录因子，参与脱落酸（ABA）信号转导[29−33]。
SOS信号通路是调控植物耐受盐胁迫的重要途径之一，在植物中较为保守，可调节盐胁迫下Na+的稳态[21]。植物受到盐胁迫时，胞内Ca2+浓度升高，Ca2+传感器SOS3/CBL4与Ca2+结合，激活丝氨酸/苏氨酸蛋白激酶SOS2/CIPK24[34−36]。受到激活的SOS2/CIPK24将位于细胞膜上的Na+/H+逆向转运蛋白SOS1/NHX7磷酸化，有活性的SOS1/NHX7把细胞内Na+转运至胞外，使植物细胞保持离子平衡[37−38]。
PKS5也能够负调控SOS信号通路，PKS5可以与SOS2相互作用并使其Ser294位点磷酸化，促进SOS2与14-3-3蛋白的相互作用，抑制SOS2活性。然而盐胁迫可诱导胞质Ca2+浓度增加，降低了14-3-3与SOS2的相互作用，增强了14-3-3与PKS5的相互作用，抑制了PKS5对SOS2的磷酸化作用[39−42]。此外，PKS5是质膜H+-ATP酶的负调节因子[41]。PKS5可磷酸化质膜H+-ATP酶AHA2的C端Ser-931位点，负向调控质膜H+-ATP酶的活性，并且在Ca2+结合蛋白SCaBP1存在的情况下，这种磷酸化作用降低[41−42]。
胡杨（Populus euphratica）是典型的耐盐乔木。本实验室前期研究发现，胡杨PeRIN4、PeAPY1/2、PeREM1.3、PeJ3、PeJRL基因均能够提高拟南芥的耐盐性。PeRIN4可以增强H+泵的质子动力势，抑制质膜的去极化，从而提高转基因拟南芥的耐盐性[43]。PeAPY1/2能够提高三磷酸腺苷双磷酸酶的活性，下调eATP浓度和活性氧水平，同时通过保持抗氧化酶活性来抑制H2O2的水平，提高植物的耐盐性[44]。过表达PeREM1.3的烟草（Nicotiana tabacum）的过氧化物酶（POD）、过氧化氢酶（CAT）和超氧化物歧化酶（SOD）活性显著提高，并且与耐盐相关的基因SOS1、HAK、NHA1、VAG1和PMA4的转录水平也显著增高[45]。PeJRL能够上调SOS1、AHA1和AHA2基因的表达，通过限制超氧阴离子的产生、增强抗氧化酶的活性，使拟南芥在盐胁迫下保持离子平衡[46]。PeJ3会激活H+-ATP酶，促进Na+/H+在质膜上的交换，减少去极化引起的K+外流，刺激H2O2信号的产生，从而增加胞质Ca2+浓度，并通过SOS途径促进Na+的外排，提高植物耐盐性[47]。本文在实验室研究背景与已有成果基础上，在胡杨中鉴定得到PePKS5基因，研究了胡杨PePKS5基因在盐胁迫下的表达量变化，以及转PePKS5基因的拟南芥在盐胁迫下的表型和生理生化反应，明确了PePKS5在植物耐盐性中的作用，为培育优良的耐盐杨树品种、拓展其在生态修复中的应用、有效提升盐碱地治理效果提供参考。
1. 材料与方法
1.1 实验材料
胡杨幼苗（1年生）于2021年4月栽种于北京林业大学苗圃。拟南芥野生型种子、亚细胞定位载体pGreen1300GFP和ABA受体PYR1-mCherry菌株保存于实验室。pK2GW7表达载体、Na+特异性荧光探针（CoroNa-Green AM）及H2O2特异性荧光探针（H2DCFDA/DCFH-DA）购买自Invitrogen公司。大肠杆菌DH5α感受态细胞和农杆菌GV3101购买自上海唯地生物技术有限公司，RNA提取试剂盒购买自艾德莱科技有限公司，抗氧化物酶检测试剂盒购买自索莱宝生物技术有限公司，其他试剂由北京擎科生物公司提供，引物合成及测序由北京睿博兴科公司完成。
1.2 PePKS5基因克隆与序列分析
1.2.1 PePKS5基因克隆
根据NCBI基因组数据库中胡杨PKS5的基因序列，以其cDNA序列为模板，使用primer5软件设计引物（表1）。提取胡杨叶片总RNA，反转录合成cDNA。以cDNA为模板进行PCR扩增，反应体系为：KOD酶25 μL；ddH2O 18 μL；cDNA 5 μL；前后引物（10 μmol/L）各1 μL。PCR反应程序为：第1阶段98 ℃ 30 s；第2阶段98 ℃ 15 s，56 ℃ 30 s，72 ℃ 30 s，30个循环；第3阶段72 ℃ 10 min；第4阶段4 ℃恒温。回收扩增产物，将纯化后的产物与pMD18-T连接，转化至大肠杆菌DH5α感受态细胞，在含有氨苄青霉素的LB平板上筛选阳性克隆并测序鉴定。
表 1 本文实验所用引物序列Table 1. Primer sequence used in this study引物名称
Primer name上游引物（5′—3′）
Forward primer (5′−3′)下游引物（5′—3′）
Reverse primer (5′−3′)PeActin7 ATTGGCCTTGGGGTTAAGAG CACACTGGAGTGATGGTTGG AtActin2 GGTAACATTGTGCTCAGTGGTGG AACGACCTTAATCTTCATGCTGC AtSOD1 AAGGAGAAACAAATCTTCAT GAGTTTGGTCCAGTAAGAGG AtCAT2 AGGATCAAACTTTGAGGGGTAG CTTGTGGTTCCTGGAATCTACT AtAPX1 AGTTTTGGATTTGATCTGTGCGTT GACGCCATCAACAACGAGTC PePKS5 ATGCCGGAGATCGAAAGTGTATCGG CTAAGTAGCCATAATCCAGGCTTA PePKS5-RT-qPCR CTGCTTATGTTGCTCCTGAG TCCTTGTCTCCGGATTCGTA 1.2.2 PePKS5氨基酸序列分析
利用生物信息学数据库（NCBI，http://www.ncbi.nhn.nih.gov/blast）获取不同植物PKS5同源氨基酸序列。利用Mega 6软件对PKS5氨基酸序列进行比对并构建系统进化树。
1.3 盐胁迫下胡杨叶片PePKS5基因表达量分析
用100 mmol/L NaCl溶液处理胡杨苗，分别在处理0、3、6、12、24、48、72 h时取胡杨叶片，提取总RNA，并反转录为cDNA。用特异性引物检测胡杨叶片PePKS5基因表达量，胡杨PeActin7为内参基因（表1）。荧光定量PCR反应程序为：第1阶段95 ℃ 1 min；第2阶段95 ℃ 10 s，55 ℃ 15 s，72 ℃ 30 s，40个循环。熔解曲线分析为：95 ℃ 15 s，60 ℃ 1 min，95 ℃ 15 s，60 ℃ 15 s。用2−ΔΔCt公式计算PePKS5基因表达量。
1.4 转基因拟南芥阳性植株的获取和筛选
1.4.1 植物表达载体的构建
用Gateway方法构建植物表达载体。设计带有attB位点的引物，PCR扩增获得带有attB位点的基因片段，通过BP反应连入pDONR221载体，形成入门克隆。反应体系为：attB-PCR产物2 μL，pDONR221（150 ng/μL） 0.5 μL，BP CloneTMII 0.5 μL，TE buffer 2 μL；反应条件为25 ℃ 1 h。回收扩增产物，并转化至大肠杆菌DH5α感受态细胞，在含有卡那霉素的LB平板上筛选阳性克隆并测序鉴定。将测序正确的菌株接种在含有卡那霉素的LB液体培养基中，37 ℃，200 r/min过夜培养，提取质粒。构建LR反应体系：attL1入门克隆产物（100 ng/μL）2 μL，PK2GW7表达载体（100 ng/μL） 0.5 μL，LR ClonaseTMII 1 μL，TE buffer 1.5 μL；反应条件为25 ℃ 1 h。回收重组产物，并转化至大肠杆菌DH5α感受态细胞，在含有壮观霉素的LB平板上筛选阳性克隆并测序鉴定。
1.4.2 转基因植株的获得
将已构建的重组质粒pPK2GW7-PePKS5和空的表达载体pPK2GW7分别转化至农杆菌GV3101感受态细胞中。在加入利福平和壮观霉素的LB平板培养基中筛选阳性克隆并测序。选取转化成功的农杆菌扩繁，通过沾花法侵染T0代拟南芥，收获的种子为T1代。将获得的拟南芥T1代种子播种到含有壮观霉素（50 mg/L）的MS培养基上，长出4片真叶后移栽到土中，收获的种子继续用壮观霉素筛选，直至获得T3代纯合体种子。使用Trizol法提取T3代野生型、转基因和转空载体株系总RNA，反转录得到cDNA后，进行半定量PCR检测和荧光定量PCR检测。荧光定量PCR反应程序为：第1阶段95 ℃ 1 min；第2阶段95 ℃ 10 s，55 ℃ 15 s，72 ℃ 30 s，40个循环。熔解曲线分析为：95 ℃ 15 s，60 ℃ 1 min，95 ℃ 15 s，60 ℃ 15 s。半定量反应程序为：第1阶段94 ℃ 5 min；第2阶段94 ℃ 30 s，56 ℃ 30 s，72 ℃ 30 s，28个循环；第3阶段72 ℃ 10 min；4 ℃恒温。扩增产物长度为200 bp，琼脂糖（1%）凝胶电泳检测。
1.5 pGreen1300GFP-PePKS5定位载体的构建和亚细胞定位
设计去除终止密码子的引物，上游引物5′端加上SpeI酶切位点，下游引物5′端加上KpnI酶切位点（表1）。以PePKS5基因序列为模板进行PCR，同时使用SpeI和KpnI对载体pGreen1300GFP进行双酶切。回收并纯化酶切产物和PCR产物，用同源重组酶连接后转化至大肠杆菌DH5α感受态细胞中，在含有卡那霉素的LB平板上筛选阳性克隆并测序鉴定。提取质粒并转化至农杆菌GV3101感受态细胞中，在加入利福平和卡那霉素的LB平板培养基中筛选阳性克隆并测序。选取转化成功的农杆菌扩繁，同时，将保存于−80 ℃冰箱的PYR1-mCherry农杆菌菌种扩繁，将二者按照体积1∶1的比例均匀混合，将混合后的菌液瞬时转化烟草叶片，室温暗培养2 d后，用激光共聚焦显微镜观测PePKS5的亚细胞定位。
1.6 盐胁迫下转基因拟南芥种子生存率和根长测定
将野生型、转空载体和转基因株系的种子分别播种于含有0和100 mmol/L的NaCl的MS培养基上。4 ℃处理2 d后置于恒温培养箱中，培养条件为22 ℃，16 h光照/8 h黑暗，记录7 d后幼苗生存率，竖直生长10 d后，拍照并记录植株的根长。实验均重复3次。
1.7 盐胁迫下拟南芥根尖Na+和K+离子流测定
将野生型、转空载体和转基因株系的种子分别播种于MS培养基上生长7 d，然后移至含有0和100 mmol/L NaCl的MS液体培养基中处理12 h。使用非损伤微测技术检测各株系幼苗根尖分生区的Na+和K+离子流。每个株系测定3个重复。
1.8 盐胁迫下转基因拟南芥Na+含量和H2O2含量测定
Na+含量测定。将在MS固体培养基上生长7 d的拟南芥各株系幼苗移至含有0和100 mmol/L NaCl的MS液体培养基中处理12 h。将幼苗移至含有Na+特异性荧光探针的10 mmol/L MS缓冲液中，室温黑暗孵育2 h，蒸馏水清洗4次，用Leica SP8激光共聚焦显微镜（德国Leica）观察并测定Na+特异性荧光探针的荧光强度，激发波长为488 nm，发射波长为510~530 nm，相对荧光强度通过Image J软件计算。
H2O2含量测定。将在MS固体培养基上生长7 d的拟南芥各株系幼苗移至含有0和100 mmol/L NaCl的MS液体培养基中处理12 h。将幼苗移至含有H2O2特异性荧光探针的10 mmol/L MS缓冲液中，室温黑暗孵育15 min，蒸馏水清洗4次，用Leica SP8激光共聚焦显微镜（德国Leica）观察并测定H2O2特异性荧光探针的荧光强度，激发波长为488 nm，发射波长为510~530 nm，相对荧光强度通过Image J软件计算。
1.9 盐胁迫下转基因拟南芥抗氧化酶活性及相关基因表达水平测定
将拟南芥各株系种子播种在含有0和100 mmol/L NaCl的培养基上，生长10 d后取样。测定过氧化物酶（POD）、过氧化氢酶（CAT）和超氧化物歧化酶（SOD）活性；提取总RNA并反转录合成cDNA，通过荧光定量PCR仪检测抗氧化酶相关基因AtSOD1、AtAPX1和AtCAT2基因的转录水平，以拟南芥AtActin2基因为内参。
1.10 盐胁迫下转基因拟南芥生理参数测定
将野生型、转空载体和转基因拟南芥株系的种子播种在MS固体培养基上，低温处理后置于培养箱中正常生长，分化出4片真叶时，挑选长势一致的幼苗分别移栽到土中正常浇水培养15 d，用100 mmol/L NaCl溶液处理15 d，测定叶绿素荧光参数、叶绿素相对含量和光合参数。
用调制叶绿素荧光仪Junior-PAM（德国WALZ）对暗处理30 min后的拟南芥叶片进行叶绿素荧光参数的测定，包括PSⅡ最大光量子效率（Fv/Fm）、实际光合量子产量（YⅡ）和相对电子传递速率（ETR）。每株系重复测定3次，取平均值。用手持式叶绿素仪SPAD-502-PLUS（日本Minolta）测定植物SPAD值，作为叶绿素相对含量值。每个株系重复3次，取平均值。用LI-6800便携式光合测量仪（美国LI-COR）检测各株系拟南芥的光合参数，包括净光合速率（Pn）、蒸腾速率（Tr）、气孔导度（Gs）和胞间二氧化碳浓度（Ci）。每个株系重复测定3次，记录平均值。
1.11 数据分析
实验数据通过Excel、Graphpad Prism8、Mega 6、DNAMAN软件进行处理、统计和绘图。通过SPSS 19.0进行单因素方差分析，显著性水平均小于0.05。
2. 结果与分析
2.1 PePKS5基因序列分析
PePKS5基因的CDS序列编码417个氨基酸。序列比对结果表明：PePKS5氨基酸序列与拟南芥（Arabidopsis thaliana）、毛果杨（Populus trichocarpa）、毛白杨（Populus tomentosa）、萝卜（Raphanus sativus）、水稻（Oryza sativa）、玉米（Zea mays）、甘蓝（Brassica oleracea）、棉花（Gossypium hirsutum）、大豆（Glycine max）、番茄（Solanum lycopersicum）、白桦（Betula platyphylla）、芥菜（Capsella rubella）和可可（Theobroma cacao）的PKS5氨基酸序列的同源性保持在53.19% ~ 98.08%之间，说明PePKS5在进化过程中较为保守（图1A）。系统进化树分析结果表明：胡杨PePKS5与毛白杨PtPKS5氨基酸亲缘关系最近（图1B）。
![]()
图 1 胡杨PePKS5氨基酸序列比对（A）与进化树构建（B）Figure 1. Amino acid sequence alignment of PePKS5 in Populus euphratica (A) and construction of evolutionary tree (B)2.2 盐胁迫下PePKS5基因在胡杨叶片中的表达量变化
分别计算盐处理0、3、6、12、24、48、72 h后胡杨叶片PePKS5基因的表达量发现：随着NaCl处理时间的增加，胡杨PePKS5的表达量在处理6 h后显著上升，12 h后达到最高值，约为0 h时表达量的2倍，24 h后开始下降，至72 h时恢复至最初状态（图2）。
![]()
图 2 盐胁迫（100 mmol/L NaCl）下胡杨叶片中PePKS5基因表达量的变化不同小写字母表示差异显著（P < 0.05）。下同。Different letters represent significant differences at P < 0.05. The same below.Figure 2. Changes of PePKS5 gene expression in leaves of Populus euphratica under salt stress (100 mmol/L NaCl)2.3 PePKS5转基因拟南芥的筛选与鉴定
使用Trizol法提取T3代转基因拟南芥、转空载体（VC）拟南芥和野生型（WT）拟南芥叶片的总RNA，进行荧光定量PCR和半定量PCR检测。结果显示：各株系拟南芥内参基因AtActin2表达一致，并且6个转基因株系均扩增出目的片段（200 bp），WT和VC株系中没有检测到目的基因PePKS5的表达（图3A）。选择相对表达量高的2个转基因株系（PePKS5-OE10和PePKS5-OE15）进行后续实验（图3B）。
![]()
图 3 PePKS5转基因拟南芥株系的筛选（A）与PePKS5表达量测定（B）WT. 野生型；VC. 转空载体株系；OE. 转基因株系。下同。WT, wild type；VC, empty vector line；OE, transgenic line.The same below.Figure 3. Screening of PePKS5 transgenic lines of Arabidopsis thaliana (A) and determination of PePKS5 expression (B)2.4 PePKS5的亚细胞定位
将带有GFP标签的重组载体瞬时转化至烟草中，观察绿色荧光在细胞内的分布情况。结果显示PePKS5与GFP的融合蛋白定位于细胞质与细胞核中。为了进一步确定PePKS5的定位，将PePKS5与GFP的融合蛋白与ABA的受体PYR1-mCherry同时在烟草细胞中瞬时表达。PYR1-mCherry定位于细胞质与细胞核中[48]，PePKS5-GFP的绿色荧光与PYR1-mCherry的红色荧光重叠，说明PePKS5定位于细胞质与细胞核中（图4）。
2.5 PePKS5过表达拟南芥株系的耐盐表型分析
在无盐培养基上，各株系拟南芥长势差别不大；经过NaCl处理后，各株系拟南芥的生长均受到抑制，然而转基因株系（PePKS5-OE10和PePKS5-OE15）的主根明显长于野生型（WT）与转空载体（VC）株系（图5A，B），并且PePKS5-OE10和PePKS5-OE15株系的生存率为81.51% ~ 83.54%，高于WT（60.5%）和VC（58%）株系（图5C，D），推测PePKS5基因能够提高拟南芥的耐盐性。
![]()
图 5 NaCl处理对拟南芥幼苗生存率和根长生长的影响A. NaCl对根系生长的影响；B.根系生长分析；C. NaCl对幼苗生存率的影响；D.幼苗生存率统计分析。A, effects of NaCl on root growth; B, statistical analysis of root growth; C, effects of NaCl on seedling survival rate; D, statistical analysis of seedling survival rate.Figure 5. Effects of NaCl treatment on seedling survival rate and root growth of Arabidopsis thaliana2.6 盐胁迫下拟南芥根尖Na+含量的测定
无NaCl处理时，WT和VC株系与PePKS5-OE10和PePKS5-OE15株系根尖Na+含量较低且无显著差异。经NaCl处理后，各株系荧光强度增强，但PePKS5-OE10和PePKS5-OE15株系的荧光强度显著低于WT和VC株系，说明NaCl处理后，转基因株系根尖细胞积累的Na+更少（图6）。
![]()
图 6 NaCl处理对拟南芥根尖细胞Na+荧光强度的影响Figure 6. Effects of NaCl treatment on Na+ fluorescence intensity in root tip cells of Arabidopsis thaliana2.7 盐胁迫下拟南芥根尖H2O2含量的测定
无NaCl处理时，WT和VC株系与PePKS5-OE10和PePKS5-OE15株系根尖H2O2含量较低且无显著差异。经NaCl处理后，各株系荧光强度增强，但PePKS5-OE10和PePKS5-OE15株系的荧光强度显著低于WT和VC株系，说明NaCl处理后，转基因株系根尖细胞中积累的H2O2更少（图7）。
![]()
图 7 NaCl处理对拟南芥根尖细胞H2O2荧光强度的影响Figure 7. Effects of NaCl treatment on H2O2 fluorescence intensity in root tip cells of Arabidopsis thaliana2.8 盐胁迫下拟南芥根尖离子流测定
Na+流测定结果显示：无NaCl处理时，各株系拟南芥根尖Na+表现出轻微外流，且相差不大。经NaCl处理后，各株系Na+外流速度均大幅度提高，并且PePKS5-OE10和PePKS5-OE15株系的Na+外流速度显著高于WT和VC株系，说明PePKS5能显著提高拟南芥外排Na+的能力（图8A）。
![]()
图 8 NaCl处理对拟南芥根尖Na+（A）和K+（B）离子流的影响纵坐标正值表示外流，负值表示内流。Positive values on the vertical coordinate represent efflux, while negative values represent influx.Figure 8. Effects of NaCl treatment on Na+ (A) and K+ (B) fluxes in root tips of Arabidopsis thalianaK+流测定结果显示：无NaCl处理时，各株系拟南芥根尖K+表现出轻微内流，且相差不大。经NaCl处理后，各株系K+的内流现象明显增强，并且PePKS5-OE10和PePKS5-OE15株系的K+内流现象更为明显，说明PePKS5能够减少拟南芥根尖K+流失（图8B）。
2.9 盐胁迫下拟南芥的抗氧化酶活性及基因表达量的变化
POD、CAT和SOD活性测定结果显示：经NaCl处理后，PePKS5-OE10和PePKS5-OE15株系的POD活性呈上升趋势，而WT和VC株系呈下降趋势（图9A）；WT和VC株系的CAT活性无明显变化，但PePKS5-OE10和PePKS5-OE15株系的CAT活性显著升高（图9B）；WT和VC株系的SOD活性无显著变化，但PePKS5-OE10和PePKS5-OE15株系的SOD活性略微下降（图9C）。APX1、CAT2和SOD1基因表达量测定结果显示：经NaCl处理后，WT和VC株系的APX1和CAT2基因表达量无明显变化，但PePKS5-OE10和PePKS5-OE15株系的APX1和CAT2基因表达量显著提高（图9D，E）；WT和VC株系的SOD1基因表达量显著上升，但PePKS5-OE10和PePKS5-OE15株系的SOD1基因表达量略微下降（图9F）。以上结果说明转基因株系的抗氧化能力较强，可以清除体内过多的H2O2。
![]()
图 9 NaCl处理对拟南芥抗氧化酶活性及相关基因表达量的影响Figure 9. Effects of NaCl treatment on the activity of antioxidant enzyme and the expression of related genes in Arabidopsis thaliana2.10 盐胁迫下拟南芥叶绿素荧光参数和叶绿素相对含量变化
图10显示，无NaCl处理时，各株系拟南芥的叶绿素荧光参数没有明显差异。经NaCl处理15 d后，各株系拟南芥的叶绿素荧光参数均呈下降趋势，但PePKS5-OE10和PePKS5-OE15株系的实际光合量子产量高于WT和VC株系，说明转基因株系的捕光蛋白复合体在盐胁迫下破坏程度相对较小，光能转化效率较高，盐胁迫对转基因株系的光反应阶段影响较小。
无NaCl处理时，各株系拟南芥的叶绿素相对含量没有显著差异。经NaCl处理15 d后，各株系拟南芥的叶绿素相对含量都有所下降，但PePKS5-OE10和PePKS5-OE15株系的叶绿素相对含量高于WT和VC株系，说明转基因株系的叶绿素合成过程受到的影响较小，对盐胁迫的耐受能力较强（图11）。
![]()
图 11 NaCl处理对拟南芥叶绿素相对含量的影响SPAD. 叶绿素相对含量。SPAD, relative chlorophyll content.Figure 11. Effects of NaCl treatment on the relative chlorophyll content in Arabidopsis thaliana2.11 盐胁迫下拟南芥的光合参数变化
无NaCl处理时，与WT和VC株系相比，PePKS5-OE10和PePKS5-OE15株系的净光合速率（Pn）、蒸腾速率（Tr）和气孔导度（Gs）均存在显著差异。经NaCl处理15 d后，各株系拟南芥的Pn值均降低（图12A）。Gs与Tr成正比，经NaCl处理15 d后，PePKS5-OE10和PePKS5-OE15株系的Tr和Gs保持相对稳定，而WT和VC株系的Tr和Gs显著上升（图12B，D），说明过表达PePKS5株系在盐胁迫下能保持相对稳定的蒸腾速率，减少植物的水分消耗。胞间二氧化碳浓度（Ci）与净光合作用有关，经NaCl处理15 d后，PePKS5-OE10和PePKS5-OE15株系的Ci保持相对稳定，而WT和VC株系的Ci则显著升高（图12C），说明WT和VC株系的碳同化作用受到抑制，不能正常同化CO2，而转基因株系的碳同化作用保持相对稳定，在一定程度上能维持正常光合作用。
![]()
图 12 NaCl处理对拟南芥光合参数的影响Pn. 净光合速率；Tr. 蒸腾速率；Ci. 胞间二氧化碳浓度；Gs. 气孔导度。Pn, net photosynthetic rate; Tr, transpiration rate; Ci, intercellular carbon dioxide concentration; Gs, stomatal conductance.Figure 12. Effects of NaCl treatment on the photosynthetic parameters of Arabidopsis thaliana3. 讨论与结论
盐处理6 h后胡杨叶片PePKS5基因表达量上调，72 h后逐渐恢复至正常水平，说明胡杨PePKS5基因能对盐胁迫做出响应（图2）。蛋白质的亚细胞定位与其功能密切相关，胡杨PePKS5定位于细胞核和细胞质中（图4），推测其可能在细胞核或细胞质中发挥功能。不同物种PKS5氨基酸序列的比对结果显示胡杨PePKS5在进化上较为保守，并且系统进化树分析结果显示胡杨PePKS5与毛白杨PtPKS5家族亲缘关系最近（图1A和图1B）。
为了探究胡杨PePKS5调节植物耐盐的生理与分子机制，本文从胡杨叶片中克隆得到PePKS5基因，将其在拟南芥中过表达并得到稳定转化的纯合体植株（图3）。初步分析各株系拟南芥的耐盐表型发现：在盐胁迫下，过表达PePKS5拟南芥株系（PePKS5-OE10和PePKS5-OE15）的根长和生存率受到的抑制程度显著低于野生型（WT）和转空载体（VC）株系，说明过表达PePKS5拟南芥株系的耐盐性更强（图5）。
盐胁迫导致植物根尖积累大量Na+，Na+过度积累引起植物体内活性氧积累，并抑制体内抗氧化酶的活性[49]。SOD能够催化超氧阴离子自由基歧化生成H2O2，H2O2可被CAT和POD分解成氧和水，使得H2O2不与O2−在铁螯合物作用下反应生成非常有害的−OH，从而使细胞免于遭受H2O2的毒害[50]。通过进一步分析盐胁迫下各株系拟南芥的生理及分子水平的生理指标发现：一方面，与WT和VC株系相比，过表达PePKS5拟南芥株系根尖Na+含量和H2O2含量较低（图6和图7），并且Na+外流和K+内流现象较为明显（图8）。另一方面，过表达PePKS5拟南芥株系的POD和CAT的活性以及APX1和CAT2基因表达水平均显著高于WT和VC株系（图9）。说明盐胁迫下过表达PePKS5拟南芥株系具有较强的排出Na+、吸收K+的能力及较强的分解H2O2的能力，从而降低了体内活性氧的积累，减弱了H2O2对抗氧化酶系统的损伤，增强了植物抗氧化能力，从而抵御盐胁迫带来的生理伤害。
盐胁迫会抑制植物对叶绿素的吸收和利用，影响类囊体的超微结构并破坏植物光合色素和光合膜系统[51]。叶绿素相对含量和叶绿素荧光参数能反映叶片吸收、传递和转换光能的能力，因此常被用作表示受到环境胁迫程度的生理指标[52]。对盐胁迫下各株系拟南芥的光合作用指标进行分析发现：一方面，过表达PePKS5拟南芥株系的叶绿素相对含量、PSⅡ最大光量子效率、实际光合量子产量和相对电子传递速率均显著高于WT和VC株系（图10和图11），说明盐胁迫下过表达PePKS5拟南芥株系的叶绿素合成和光合电子传递过程受到的影响相对较小，光能转化效率相对较高。另一方面，过表达PePKS5拟南芥株系的净光合速率相对较高，而胞间CO2浓度、气孔导度、蒸腾速率均低于WT和VC株系（图12），说明盐胁迫下过表达PePKS5拟南芥株系能通过调节气孔开度，减少对水分的消耗，保持较稳定的碳同化能力，从而维持相对稳定的光合作用和蒸腾作用。
![]()
图 10 NaCl处理对拟南芥叶绿素荧光参数的影响YⅡ. 实际光合量子产量；Fv/Fm. PSⅡ最大光量子效率；ETR. 相对电子传递速率。YⅡ, actual photosynthetic quantum yield; Fv/Fm, maximum photochemical quantum efficiency of PSⅡ; ETR, relative electron transfer rate.Figure 10. Effects of NaCl treatment on the chlorophyll fluorescence parameters of Arabidopsis thaliana综上，本文从离子平衡、活性氧平衡及光合作用3个角度对胡杨PePKS5基因的耐盐性进行研究，得出结论：过表达PePKS5提高了转基因拟南芥的耐盐性，主要通过增强Na+的外排能力，维持活性氧平衡状态，以及保持相对稳定的光合作用能力。本研究初步明确了胡杨PePKS5在植物响应盐胁迫中的作用，为培育优良的耐盐杨树品种、拓展其在生态修复中的应用、有效提升盐碱地治理效果提供了参考。
目前对于PKS5在植物响应盐胁迫中的作用研究较少。Fuglsang等[41]发现：拟南芥PKS5是质膜H+-ATP酶的负调节因子，在拟南芥对盐胁迫的耐受性中起负向调控作用。胡杨PKS5与拟南芥PKS5的功能不一致，推测可能是由于胡杨与拟南芥亲缘关系较远而导致彼此功能不同。因此，胡杨PePKS5调控体内活性氧平衡及离子平衡的机制还有待更深一步的研究。后续研究一方面可以在胡杨中验证PePKS5基因的功能，另一方面可以鉴定出与PePKS5相互作用的底物蛋白，在转录调控与翻译后修饰的分子水平上，建立PePKS5参与调节胡杨耐盐的信号通路，并阐明PePKS5调控胡杨耐盐的分子机理。
-
![]()
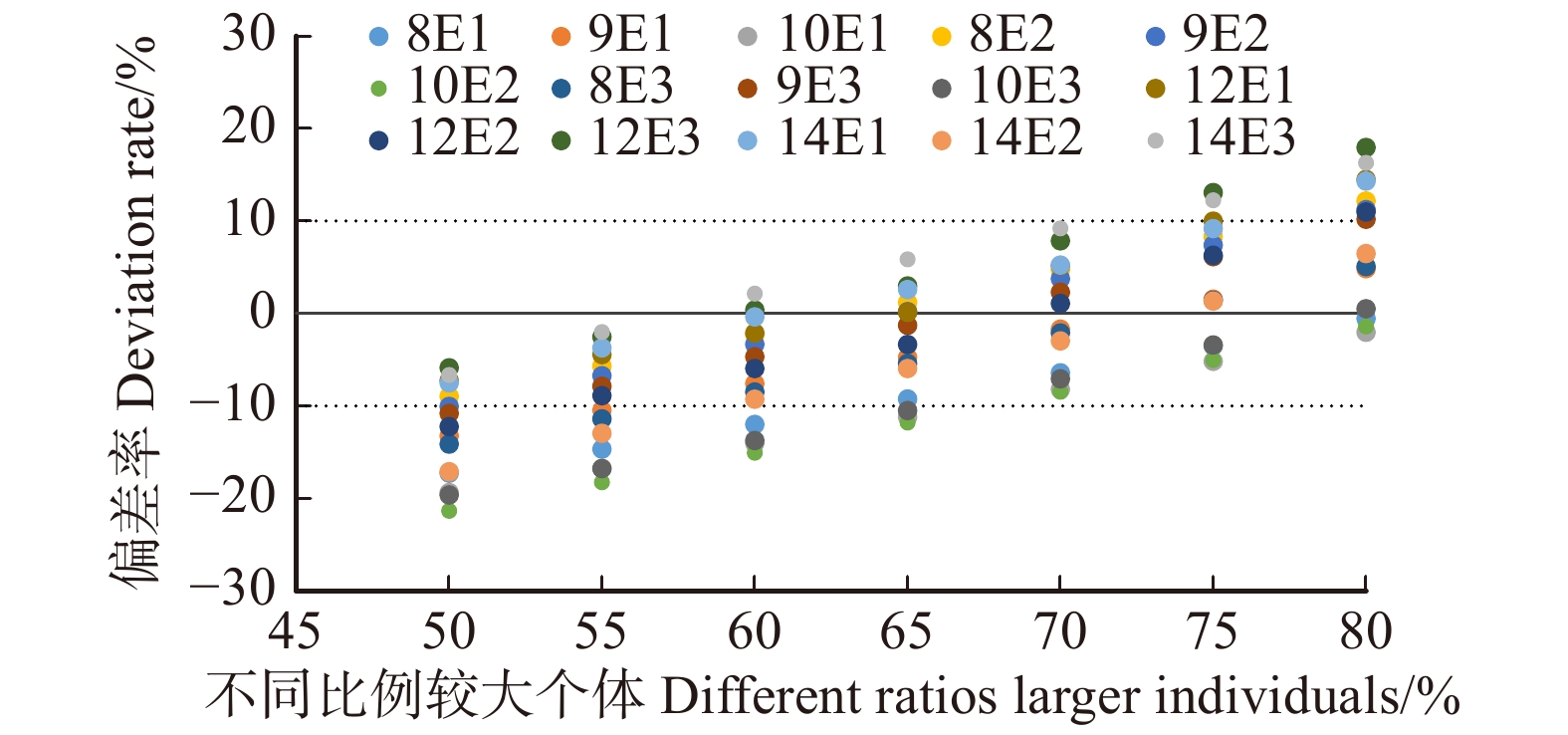
图 1 潜在最大断面积与标准断面积的偏差率
E1、E2、E3表示E密度的3次重复，E代表密度为10 000株/hm2；8 ~ 14代表林分年龄。下同。E1, E2, E3 represent three repetitions under “E” density; E indicates the density is 10 000 trees/ha; 8−14 indicate the stand’s age. The same below.
Figure 1. Deviation rate between potential maximum basal area and standard basal area
![]()
图 2 潜在疏密度与疏密度的偏差率
Figure 2. Deviation rate between potential density of stocking and density of stocking
![]()
图 3 林分断面积与潜在最大断面积的回归分析
Figure 3. Regression analysis of stand basal area and potential maximum basal area
表 1 天然林林分基本概况
Table 1 Basic situation of natural forest
样地
Sample plot天然林类型
Natural forest type平均胸径
Average DBH/cm林分密度/（株·hm− 2）
Stand density (tree·ha− 1)坡度
Slope degree/(°)坡向
Slope aspect森林面积
Forest area/m2a 红松阔叶混交林
Pinus koraiensis-broadleaf mixed forest18.11 1 186 17 西北 Northwest 100 × 100 b 22.46 800 9 西北 Northwest 100 × 100 c 21.81 748 11 北 North 100 × 100 d 20.78 824 12 北 North 100 × 100 h 栎类针阔混交林
Conifer-broadleaf forest dominated by Quercus spp.17.03 1 266 21 东 East 30 × 30 i 16.15 1 833 31 南 South 70 × 70 j 栎类阔叶混交林
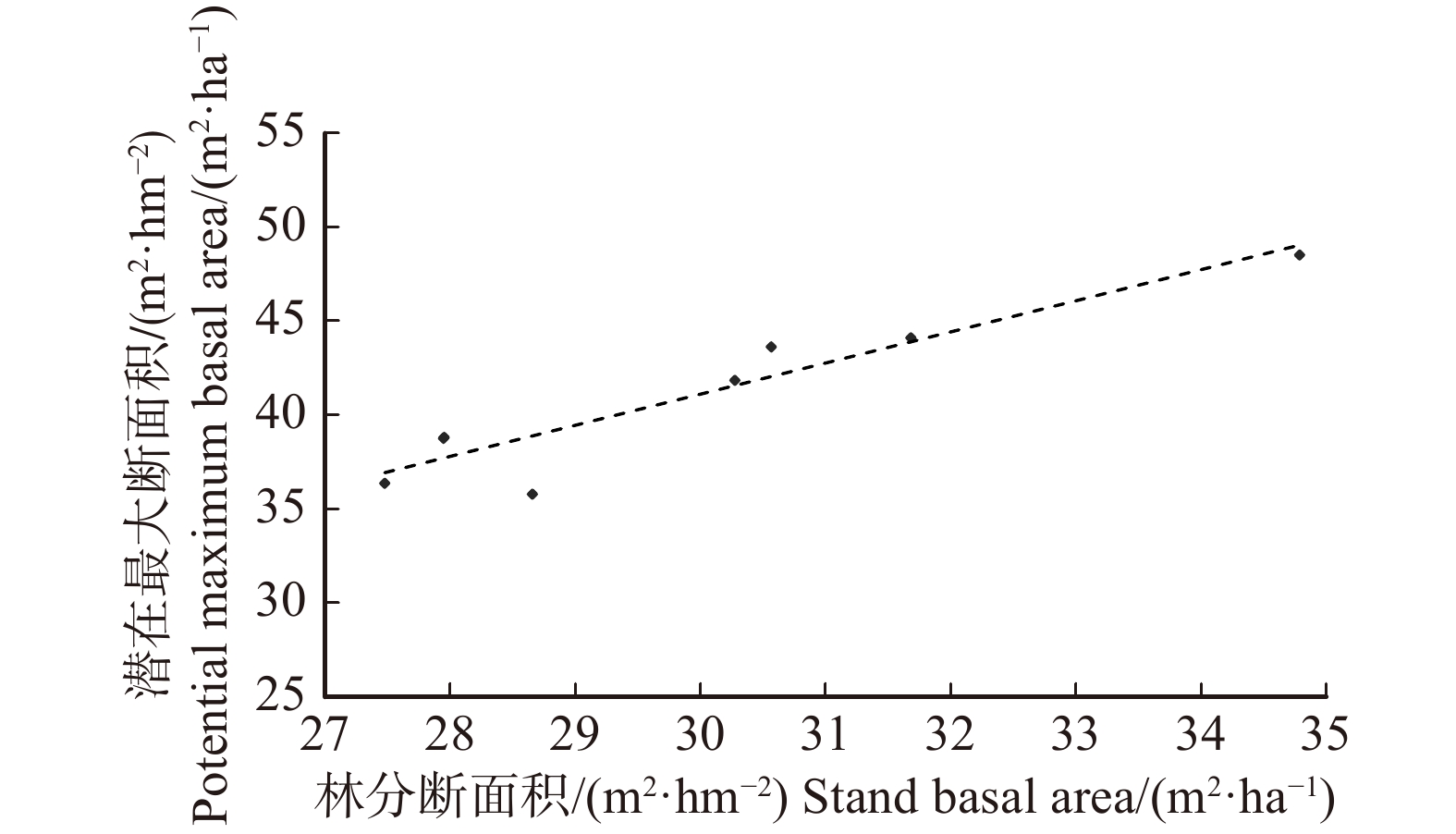
Broadleaf mixed forest dominated by Quercus spp.13.81 1 478 32 西南 Southwest 70 × 70 k 17.05 1 336 37 东北 Northeast 60 × 60 
下载: 导出CSV
表 2 不同天然林样地潜在疏密度
Table 2 Potential density of stocking of different natural forests
样地
Sample plot断面积/（m2·hm− 2）
Basal area/(m2·ha− 1)潜在最大断
面积/（m2·hm− 2）
Potential maximum
basal area/(m2·ha− 1)潜在疏密度
Potential density
of stockinga 30.57 43.62 0.70 b 31.68 44.12 0.72 c 27.95 38.81 0.72 d 27.95 38.76 0.72 h 34.79 48.51 0.72 i 30.27 41.84 0.72 j 27.48 36.36 0.76 k 28.66 35.78 0.80
下载: 导出CSV
-
[1] 惠刚盈, 张弓乔, 赵中华, 等. 天然混交林最优林分状态的π值法则[J]. 林业科学, 2016, 52(5):1−8. Hui G Y, Zhang G Q, Zhao Z H, et al. A new rule of π value of natural mixed forest optimal stand state[J]. Scientia Silvae Sinicae, 2016, 52(5): 1−8.
[2] 赵中华, 惠刚盈, 胡艳波, 等. 基于大小比数的林分空间优势度表达方法及其应用[J]. 北京林业大学学报, 2014, 36(1):78−82. Zhao Z H, Hui G Y, Hu Y B, et al. Method and application of stand spatial advantage degree based on the neighborhood comparison[J]. Journal of Beijing Forestry University, 2014, 36(1): 78−82.
[3] Graz F P, Gadow K V. Application of a “stem number guide curve ” for sustainable harvest control in the dry woodland savanna of northern Namibia[J]. Journal of the South African Forestry Association, 2005, 204(1): 37−44. doi: 10.2989/10295920509505225
[4] 甄学宁. 马尾松和杉木用材林基准林分的探讨[J]. 森林与环境学报, 1995, 15(2):146−150. Zhen X N. Probe into the problems of the Quasi- standard stand of Pinus massoniana andCunninghamia lanceolata timber forest[J]. Journal of Forest and Environment, 1995, 15(2): 146−150.
[5] 杜纪山, 李悦黎. 混交林疏密度的计算[J]. 陕西林业科技, 1992(1):32−35. Du J S, Li Y L. Calculation of the density for mixed forest[J]. Shaanxi Forest Science and Technology, 1992(1): 32−35.
[6] 段爱国, 张建国, 孙洪刚, 等. 林分断面积生长模拟理论与技术研究[J]. 世界林业研究, 2013, 26(2):43−47. Duan A G, Zhang J G, Sun H G, et al. Research progress of growth simulation theories and technologies for stand basal area[J]. World Forestry Research, 2013, 26(2): 43−47.
[7] Hui G Y. Wuchsmodelle fuer die Baumart Cunninghamia lanceolata[D]. Göttingen: Cuvillier Verlag Göttingen, 1998.
[8] 孙洪刚. 杉木人工林断面积生长规律及动态模拟[D]. 北京: 中国林业科学研究院, 2008. Sun H G. Basal area growth and model prediction in Cunninghamia lanceolata Plantation[D]. Beijing: Chinese Academy of Forestry, 2008.
[9] 张雄清, 张建国, 段爱国. 基于贝叶斯法估计杉木人工林树高生长模型[J]. 林业科学, 2014, 50(3):69−75. Zhang X Q, Zhang J G, Duan A G. Tree-height growth model for Cunninghamia lanceolata plantation based on bayesian method[J]. Scientia Silvae Sinicae, 2014, 50(3): 69−75.
[10] 童书振, 刘景芳. 全国杉木断面积、蓄积量标准表的编制[J]. 林业科技通讯, 1989, 10(8):9−11. Tong S Z, Liu J F. Establishment of national standard table for basal area and volume of Cunninghamia lanceolata[J]. Forest Science and Technology, 1989, 10(8): 9−11.
[11] 杜纪山, 唐守正. 林分断面积生长模型研究评述[J]. 林业科学研究, 1997, 10(6):599−606. Du J S, Tang S Z. The review of studies on stand basal area growth model[J]. Forest Research, 1997, 10(6): 599−606.
[12] Bennett F A, Clutter J L. Multiple-product yield estimates for unthinned slash pine plantations[M]. New York: NTIS United States, 1983: 71−72
[13] Rodríguez F, Pemán J, Aunós Á. A reduced growth model based on stand basal area: a case for hybrid poplar plantations in northeast Spain[J]. Forest Ecology & Management, 2010, 259(10): 2093−2102.
[14] 惠刚盈, 赵中华, 胡艳波, 等. 我国西北主要天然林经营模式设计[J]. 林业科学研究, 2016, 29(2):155−161. doi: 10.3969/j.issn.1001-1498.2016.02.001 Hui G Y, Zhao Z H, Hu Y B, et al. Management models for natural forests in northwestern China[J]. Forest Research, 2016, 29(2): 155−161. doi: 10.3969/j.issn.1001-1498.2016.02.001
[15] H·萨利科夫, B·阿什梅特科夫, 邓钦生, 等. 按优势木平均胸径及冠径确定标准断面积[J]. 华东森林经理, 1990, 4(2):47−49. Vladimir S H, Ashmetkov B, Deng Q S, et al. Standard basal area determined by mean DBH and crown diameter of dominant trees[J]. East China Forest Management, 1990, 4(2): 47−49.
-
期刊类型引用(17)
1. 高杰. 天然林保护对生态系统服务功能的影响. 农业灾害研究. 2024(02): 232-234 . 
百度学术
2. 力佳琪，麦强盛，王俊超. 玉白顶自然保护区森林生态价值评估. 农业与技术. 2024(18): 67-71 . 百度学术
3. 潘丰十，牛香，郭珂. 呼伦贝尔市典型生态产品禀赋与价值化实现路径优化. 林业科学. 2024(12): 146-157 . 百度学术
4. 严雨桐，陈花丹，游巍斌，刘进山，蔡昌棠，何东进. 基于能值分析的天宝岩泥炭沼泽生态系统服务价值评估. 生态与农村环境学报. 2023(03): 335-343 . 百度学术
5. 李保杰，褚帅，顾和和. 淮海经济区生态系统服务价值时空分异特征研究. 地域研究与开发. 2023(02): 167-172 . 百度学术
6. 魏媛，吴长勇，洪林. 碳中和导向下贵州省森林资源生态价值评估及生态补偿研究. 自然资源情报. 2023(04): 44-50 . 百度学术
7. 赵玉堂. 普达措国家公园森林生态系统服务价值评估与分析. 林业调查规划. 2023(03): 208-213 . 百度学术
8. 邓紫君，刘鑫，祖浩然，苏闪闪，陈颖，罗俊毅，闫文德，张翔，王明旭. 湖南省森林型国家级自然保护区森林生态系统服务功能价值评估. 湖南林业科技. 2023(04): 72-80 . 百度学术
9. 李连强，杨会侠，丁国泉，李虹谕，白荣芬，王品. 辽宁仙人洞国家级自然保护区森林生态服务物质量评估及权衡与协同. 北京林业大学学报. 2023(09): 83-94 . 本站查看
10. 白晓航，施佳颖. 黑龙江丰林国家级自然保护区红松+紫椴+硕桦群系优势树种生态位特征与种间联结分析. 园林. 2023(10): 14-21 . 百度学术
11. 李超，谢飞，苏学威，罗传文. 凉水国家级自然保护区森林生态系统服务功能评估. 中国林副特产. 2023(06): 17-18 . 百度学术
12. 党俊. 移植栽培技术在自然保护区天然林保护工程生态修复中的应用. 环境保护与循环经济. 2023(12): 68-71 . 百度学术
13. 张颖，刘平辉，朱传民，张林颖. 基于NPP的抚州市生态系统服务功能重要性评价. 贵州农业科学. 2022(02): 133-140 . 百度学术
14. 胡建忠. 对我国系统种植开发沙棘的回顾与建议. 防护林科技. 2022(04): 75-77 . 百度学术
15. 王晓康. 山西省关帝山国有林区森林生态系统服务功能价值估算研究. 中国农学通报. 2022(23): 49-55 . 百度学术
16. 任志华，秦磊. 黑龙江省乡村振兴战略实施下的乡村发展策略. 规划师. 2022(09): 139-144 . 百度学术
17. 张卫民. 中国自然保护地生态资产核算框架研究. 自然保护地. 2021(02): 22-30 . 百度学术
其他类型引用(15)
计量
- 文章访问数: 5266
- HTML全文浏览量: 880
- PDF下载量: 94
- 被引次数: 32
