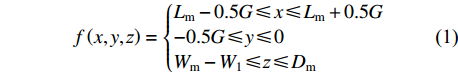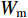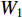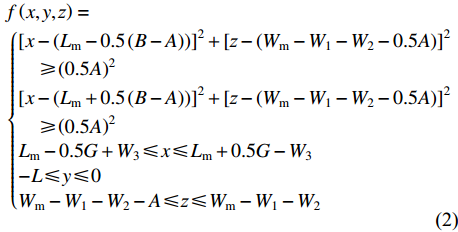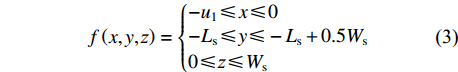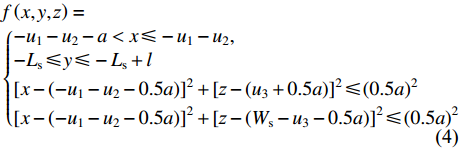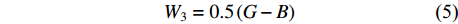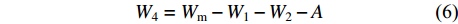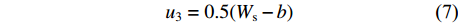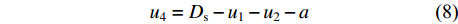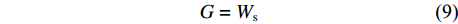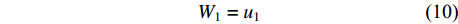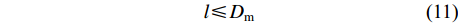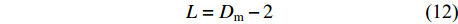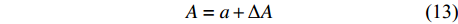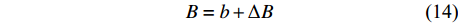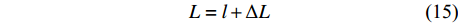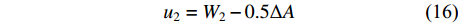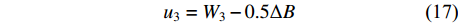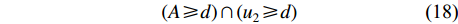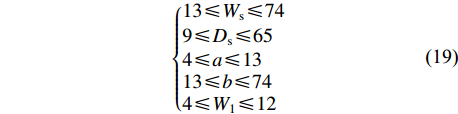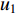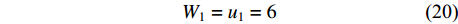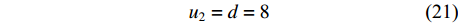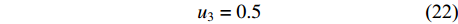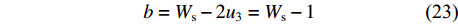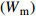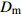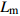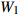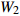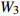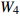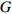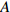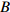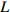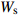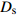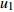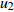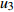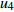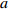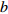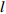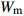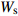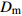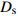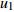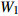Intelligent method of determining dimension of mortise and tenon joint based on parameterization
-
摘要:目的 榫卯结构尺寸的确定是编写榫卯数控加工代码的前提,也是实现榫卯数控加工的基础,但现有的通过反复修改榫卯几何模型确定榫卯尺寸的方式,效率低、难度高,严重影响了榫卯数字化加工的发展。因此,有必要设计一种榫卯尺寸智能化确定的方法。方法 以改良型格肩榫为例,首先利用参数化的设计思想,建立格肩榫的数学模型并提取了格肩榫尺寸参数;然后根据榫卯装配体零件的特征,基于装配约束,从位置关系和配合关系两个角度,建立格肩榫尺寸参数间的关系函数;再基于工艺约束,从数控加工方式、市场调研结果和工艺知识这3个方面,确定部分尺寸的取值范围和预设参考值,并建立尺寸参数与工艺约束间的关联函数;最后,以零件的断面尺寸为输入参数,整合关联函数、取值范围和预设参考值,建立尺寸参数关联函数表。结果 通过建立榫卯数学模型,提取了榫卯各类尺寸参数;根据榫卯装配和工艺约束,成功建立了榫卯尺寸参数间的函数关联,并获取了尺寸参数的取值范围和预设推荐值;通过建立尺寸参数关联函数表,实现了只需输入榫卯零件的断面尺寸,系统就可以自动输出榫卯其他尺寸参数值。结论 在装配和工艺两方面综合约束函数基础上建立的榫卯尺寸智能确定方法,是对榫卯工艺知识的数字化整理和重用,不仅能实现榫卯尺寸的智能确定,也为实现榫卯乃至实木加工的智能制造提供了基础条件。Abstract:Objective The determination of dimensions of mortise and tenon joint is the premise of editing NC(numerical control) codes of mortise and tenon joint. It is also the foundation of realizing CNC (computer numerical control) machining of mortise and tenon joint. But the existing method of determining the dimensions of mortise and tenon joint by modifying the geometric models repeatedly is low efficiency and high difficulty, which has seriously affected the development of digital machining of mortise and tenon joint. Therefore, it is necessary to design an intelligent method of determining dimension of mortise and tenon joint.Method This paper takes a modified lattice shoulder tenon as example. In the first, the mathematical models of lattices shoulder tenon were established and the dimension parameters of latticed shoulder tenon were extracted by parametric design ideas. Secondly, the correlation functions between dimension parameters of lattice tenon were established based on assembly constraints, which included two perspectives: position relation and match relation. Then, the correlation functions between dimension parameters and process constraints were established, and value ranges and preset values of part dimensions were settled based on process constraints, which included three aspects: NC machining technology, market research and process knowledge. Finally, taking the end dimensions of parts as the input parameters, integrating with associated functions, value ranges, and preset values, the relevant parameter function table was established.Result By establishing the mathematical model of mortise and tenon joint, the dimension parameters of mortise and tenon joint were extracted. According to the assembly and process constraints of mortise and tenon joint, the correlation functions between dimension parameters were established successfully, and the value ranges and the default values were obtained. By founding the correlation function table of dimension parameters, the system can automatically output other dimension parameters by just inputting the cross-section dimensions of the mortise and tenon parts.Conclusion The intelligent method of determining dimension of mortise and tenon joint was established on the combination of assembly and process constraints, that was also the scientific arrangement and reuse of process knowledge. This method can not only help to realize the intelligent determination of dimension, but also provide basic condition for intelligent manufacturing of mortise and tenon joints, even solid wood furniture processing.
-
近年来,数字化控制技术发展迅速,已被广泛应用于包括实木家具在内的各类加工制造领域,随之出现了一批针对中式家具,特别是榫卯加工的数控设备和适宜数控加工的改良榫型[1-2]。但榫卯加工的数字化程度仍与硬件设备的升级相脱节[3]。
目前多数企业的榫卯数控加工流程大致如下:首先,根据预先设计的榫卯尺寸,建立榫卯实体模型;然后,通过设计刀具路径和后置处理,生成加工代码;最后,将加工代码传送给数控机床进行加工。这种加工流程的实现,前提就是绘制尺寸精确的榫卯模型。但榫卯具有种类繁多、结构复杂且尺寸多变等特点,单纯靠传统的建模方式,会带来大量重复操作[4]。与此同时,榫卯的尺寸无标准可循,依靠少数操作者的经验而定。不合理的榫卯尺寸参数设置方式,严重影响了榫卯数字化加工效率和加工质量。因此,有必要利用参数化设计方法来解决上述问题。
以经典榫卯之一的格肩榫为例,利用参数化设计方法,以零件的断面尺寸为输入参数,从榫卯装配约束[5]和工艺约束两个角度,对榫卯尺寸进行关联设计[6-7],实现了仅需要输入榫卯零件的断面尺寸,就可以自动确定榫卯的其他尺寸数值。
1. 榫卯尺寸智能确定方法设计原则
榫卯结构相对固定,因而可以通过建立数学模型来描述榫卯结构[8]。同时,榫卯作为典型装配零件,其尺寸设置受到装配关系的约束。此外,还包括加工方式、传统工艺经验等方面的共同影响。因此,在建立榫卯数学模型的时候,就需要综合考虑这些因素,根据这些因素建立起尺寸参数间,尺寸参数与装配关系间的约束关系,从而达到智能确定榫卯尺寸的目的。
对榫卯尺寸的智能化确定方法进行研究时,需要考虑到以下原则:
(1)全面综合的原则
榫卯尺寸参数受到多方面因素的约束,且由于装配关系,会产生约束的传递[9]。为了避免遗漏重要影响因素,也为了提高参数匹配的准确性,应在兼顾装配约束的前提下,从各个方面逐一查找。
(2)手动输入参数尽可能少的原则
榫卯的尺寸参数数量繁多,逐一进行参数设定不利于加工效率的提高。因此,应该遵循尽可能减少必须要手动输入的参数数量的原则,将变动频繁的尺寸设置为必须要手动输入的参数,较稳定或是可由其他尺寸计算得出的尺寸则可以采取预设参数的方式由系统自动设置。
(3)定量与定性方法相结合的原则
单纯的定性或是定量的方法都有其局限性,榫卯的结构形式并不是一定的,而是具有一定的灵活性的。因此,应该采用定量、定性相结合的方法。例如:榫头尺寸范围的设置考虑使用定性方法,而配合尺寸的设置则考虑使用定量方法。
(4)模块化的原则
榫卯种类繁多,不同种类榫卯间由于结构差异性较大,装配约束关系也大相径庭,并没有通用的约束关系模型。因此,应该按照模块化的原则,对榫卯按结构类型进行合理的模块划分。
2. 榫卯尺寸智能确定方法设计流程
榫卯尺寸的智能化确定方法研究流程如图1所示。提出了基于装配约束的参数化设计方法:利用参数化的设计思想[10-11],建立榫卯数学模型,提取榫卯尺寸参数,基于榫卯装配体零件特质,从位置关系和配合关系两个角度,建立榫卯尺寸参数间关系函数;再基于工艺约束,从数控加工方式、市场调研结果和工艺知识这3个方面建立榫卯尺寸参数与工艺的关联函数,进一步约束和优化了榫卯尺寸参数。整合装配和工艺两方面的关联函数,建立尺寸参数关联函数表,实现尺寸参数传递。通过个别尺寸参数的设置,达到同时确定关联尺寸参数的作用,也建立了榫卯尺寸智能化确定的方法。
3. 榫卯尺寸智能确定方法实施
格肩榫是中式传统家具的典型视觉特征代表[12],同一平面上横材竖材均为方材的家具,多用此榫卯工艺,常见于椅凳类家具中横枨与腿构件的结合,柜类家具中柜身与柜门横带构件的结合中。本研究将以现有家具企业中常见的改良型格肩榫为例,利用总结出的榫卯尺寸智能确定方法,完成格肩榫尺寸的智能确定,以验证该方法的可行性。
3.1 参数化榫卯数学模型的建立
参数化是指在保持拓扑关系不变的基础上,利用参数去约束形状特征和尺寸,建立数据和模型双向智能关联[13]。参数化在建筑设计、工业制造行业已经盛行多年,近年来,家具设计中也已有不少应用[14-16]。参数化技术具体表现为尺寸驱动的几何形状修改,参数化的核心是建立关联的逻辑系统[17],参数化设计灵活可控,能避免方案修改带来的大量重复性劳动。
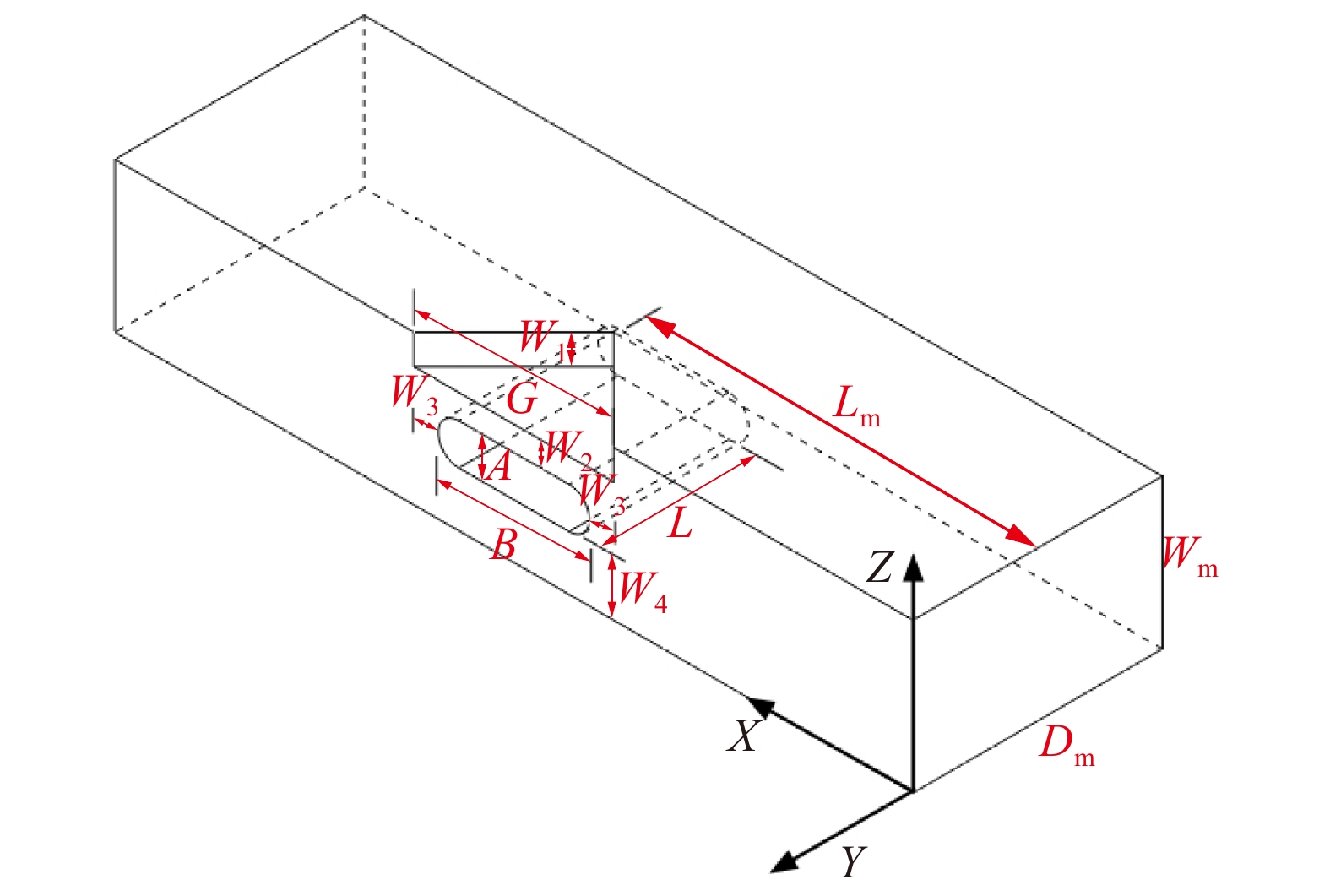
基于参数化的设计思想,本研究对格肩榫几何模型和格肩榫形状特征的几何位置控制方程,进行了参数提取。图2为某参数化CAD软件中建立的格肩榫榫眼零件的几何模型,建立了工件坐标系,坐标系原点位于模型的右下角。取材料宽度方向在Z轴正方向,材料长度方向在X轴正方向,材料厚度方向为Y轴负方向。则三角肩缺的几何位置控制方程如式(1)所示:
![]() 图 2 格肩榫榫眼零件的几何模型Wm为榫眼材料断面宽度;Dm为榫眼材料断面厚度;Lm为榫眼中心距离端面在X方向位置;G为三角肩缺底边长度;A为椭圆榫眼的宽度;B为椭圆榫眼的长度;L为椭圆榫眼的深度;W1为三角肩缺的厚度;W2为榫眼偏置(三角肩缺下边线与椭圆榫眼上边线的距离);W3为椭圆榫眼左右边距;W4为榫眼下偏置(椭圆榫眼下边线于材料底面间的距离)。Wm is the width of mortise material, Dm is the thickness of mortise material, Lm is the distance between the center of mortise and the end face in X direction, G is the length of breach, A is the wide of mortise, B is the length of mortise, L is the depth of mortise, W1 is the thickness of triangular mortise, W2 is the offset of mortise (distance between the border-bottom of triangular mortise and border-top of mortise), W3 is the margins of mortise, and W4 is the under offset of mortise (distance between the border-bottom of mortise and the underside of material).Figure 2. Geometrical model of modified lattice shoulder mortise
图 2 格肩榫榫眼零件的几何模型Wm为榫眼材料断面宽度;Dm为榫眼材料断面厚度;Lm为榫眼中心距离端面在X方向位置;G为三角肩缺底边长度;A为椭圆榫眼的宽度;B为椭圆榫眼的长度;L为椭圆榫眼的深度;W1为三角肩缺的厚度;W2为榫眼偏置(三角肩缺下边线与椭圆榫眼上边线的距离);W3为椭圆榫眼左右边距;W4为榫眼下偏置(椭圆榫眼下边线于材料底面间的距离)。Wm is the width of mortise material, Dm is the thickness of mortise material, Lm is the distance between the center of mortise and the end face in X direction, G is the length of breach, A is the wide of mortise, B is the length of mortise, L is the depth of mortise, W1 is the thickness of triangular mortise, W2 is the offset of mortise (distance between the border-bottom of triangular mortise and border-top of mortise), W3 is the margins of mortise, and W4 is the under offset of mortise (distance between the border-bottom of mortise and the underside of material).Figure 2. Geometrical model of modified lattice shoulder mortisef(x,y,z)={Lm−0.5G⩽ (1) 式中:G为三角肩缺的底边长度;
{W_{\rm{m}}} 为榫眼材料断面宽度;Dm为榫眼材料断面厚度(取正数值);Lm为榫眼中心距离端面在X方向位置(取正数值);{W_{\rm{1}}} 为三角肩缺厚度。则椭圆榫眼模型的几何位置控制方程如式(2)所示:
\begin{aligned} & f\left( {x,{{y}},{{{\textit{z}}}}} \right) = \\ & \left\{ {\begin{aligned} & {{\left[ {x - \left( {{L_{\rm{m}}} - 0.5\left( {{B} - {A}} \right)} \right)} \right]}^2} + {{\left[ {{\textit{z}} - \left( {{W_{\rm{m}}} - {W_1} - {W_2} - 0.5{A}} \right)} \right]}^2} \\ & \quad \geqslant {{\left( {0.5A} \right)}^2}\\ & {{\left[ {x - \left( {{L_{\rm{m}}} + 0.5\left( {{B} - {A}} \right)} \right)} \right]}^2} + {{\left[ {{\textit{z}} - \left( {{W_{\rm{m}}} - {W_1} - {W_2} - 0.5{A}} \right)} \right]}^2} \\ & \quad \geqslant {{\left( {0.5A} \right)}^2}\\ & {{L_{\rm{m}}} - 0.5G + {W_3} \leqslant x \leqslant {L_{\rm{m}}} + 0.5G - {W_3}}\\ & { - L \leqslant y \leqslant 0}\\ & {{W_{\rm{m}}} - {W_1} - {W_2} - {A} {\leqslant} {\textit{z}} {\leqslant} {W_{\rm{m}}} - {W_1} - {W_2}} \end{aligned}} \right. \end{aligned} (2) 式中:A为椭圆榫眼的宽度;B为椭圆榫眼的长度;L为椭圆榫眼的深度;W2为榫眼偏置(三角肩缺下边线与椭圆榫眼上边线的距离);W3为椭圆榫眼左右边距。
式(1)和式(2)也就构成了格肩榫榫眼零件的数学模型。由于格肩榫的形状固定,则其几何关系也随之固定。因此,只要确定尺寸参数,就可以根据数学模型,建立起格肩榫的几何模型。
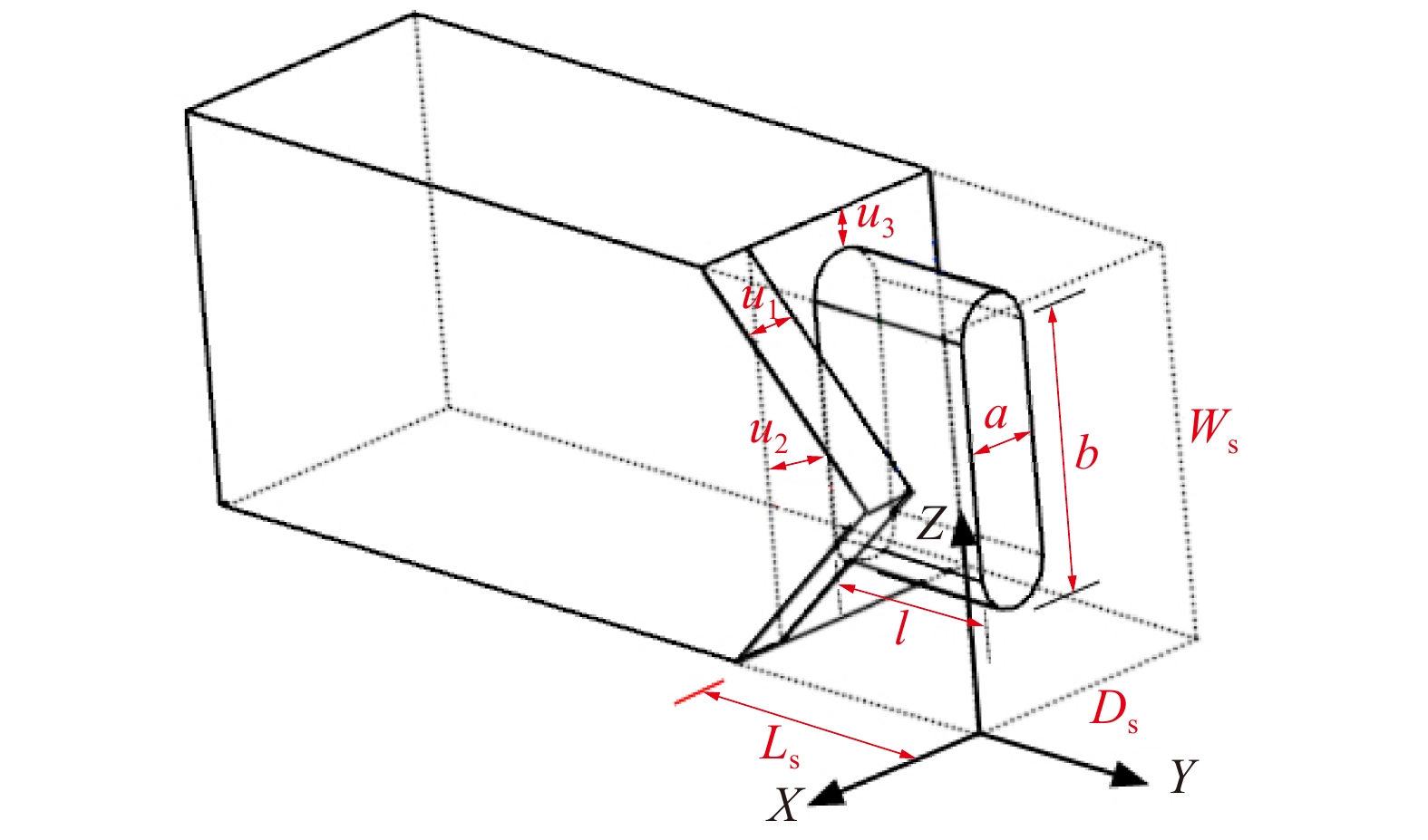
同理,完成了格肩榫榫头零件数学模型的建立和尺寸参数提取。图3为格肩榫榫头零件的几何模型,式(3)和式(4)分别为格肩榫榫头零件的数学模型。
![]() 图 3 格肩榫榫头零件的几何模型Ws为榫头材料断面宽度;Ds为榫头材料断面厚度; {L}_{\mathrm{s}} 为材料端面到榫头底面的距离;a为椭圆榫头的厚度;b为椭圆榫头的宽度;l为椭圆榫头的长度;u1为三角榫肩厚度;u2为榫头偏置;u3为椭圆榫头上下边距。Ws is the width of joint material, Ds is the thickness of joint material, Ls is the distance between the end face and the bottom of tenon, a is the thickness of tenon, b is the width of tenon, l is the length of tenon, u1 is the thickness of triangular tenon, u2 is the offset of tenon, and u3 is the margins of tenon.Figure 3. Geometrical model of modified lattice shoulder tenon
图 3 格肩榫榫头零件的几何模型Ws为榫头材料断面宽度;Ds为榫头材料断面厚度; {L}_{\mathrm{s}} 为材料端面到榫头底面的距离;a为椭圆榫头的厚度;b为椭圆榫头的宽度;l为椭圆榫头的长度;u1为三角榫肩厚度;u2为榫头偏置;u3为椭圆榫头上下边距。Ws is the width of joint material, Ds is the thickness of joint material, Ls is the distance between the end face and the bottom of tenon, a is the thickness of tenon, b is the width of tenon, l is the length of tenon, u1 is the thickness of triangular tenon, u2 is the offset of tenon, and u3 is the margins of tenon.Figure 3. Geometrical model of modified lattice shoulder tenon格肩榫的三角格肩一般均为等腰直角三角形,则三角格肩榫模型的几何位置控制方程如式(3)所示:
f\left( {x,{{y}},{\textit{z}}} \right) = \left\{ {\begin{aligned} & { - {u_1} \leqslant x \leqslant 0}\\ & { - {L_{\rm{s}}} \leqslant y \leqslant - {L_{\rm{s}}} + 0.5{W_{\rm{s}}}}\\ & {0 {\leqslant} {\textit{z}} {\leqslant} {W_{\rm{s}}}} \end{aligned}} \right. (3) 式中:Ws为榫头材料断面宽度; Ls为材料端面到榫头底面的距离;u1为三角榫肩厚度。
则椭圆榫眼模型的几何位置控制方程如式(4)所示:
\begin{aligned} & f\left( {x,{{y}},{\textit{z}}} \right) = \\ & \left\{ {\begin{aligned} & { - {u_1} - {u_2} - {{a}} < x \leqslant - {u_1} - {u_2},}\\ & { - {L_{\rm{s}}} \leqslant y \leqslant - {L_{\rm{s}}} + l}\\ & {{{\left[ {x - \left( { - {u_1} - {u_2} - 0.5a} \right)} \right]}^2} + {{\left[ {{\textit{z}} - \left( {{u_3} + 0.5a} \right)} \right]}^2} \leqslant {{\left( {0.5a} \right)}^2}}\\ & {{{\left[ {x - \left( { - {u_1} - {u_2} - 0.5a} \right)} \right]}^2} + {{\left[ {{\textit{z}} - \left( {{W_{\rm{s}}} - {u_3} - 0.5a} \right)} \right]}^2} \leqslant {{\left( {0.5a} \right)}^2}} \end{aligned}} \right. \end{aligned} (4) 式中:a为椭圆榫头的厚度;l为椭圆榫头的长度;u2为榫头偏置;u3为椭圆榫头上下边距。
3.2 榫卯尺寸参数及分类
在建立格肩榫零件数学模型的基础上,对能直接驱动榫卯结构变型的尺寸参数进行了提取和分类。从对榫卯零件结构变动作用的角度来,将榫卯尺寸参数分为断面尺寸、位置尺寸、形状尺寸3类。并根据使用习惯,对参数进行命名,表1为格肩榫的参数表。这些参数都与榫卯结构直接相关。
表 1 格肩榫的参数表Table 1. Parameter lists of lattice shoulder tenon零件名称
Component name断面尺寸参数
Cross-section dimension parameter位置尺寸参数
Location dimension parameter形状尺寸参数
Form size parameter榫眼零件
Mortise part材料宽度
Material width {(W}_{\mathrm{m}})材料厚度
Material thickness ( {D}_{\mathrm{m}} )榫眼位置
Location of mortise ( {L}_{\mathrm{m}} )三角肩缺厚度
Thickness of
triangular mortise ( {W}_{1} )榫偏置
Offset of mortise ( {W}_{2} )左右边距
Margin between bottom ( {W}_{3} )下偏置
Under offset ( {W}_{4} )肩缺底长
Length of breach ( G )榫眼宽
Width of mortise ( A )榫眼长
Length of mortise ( B )榫眼深
Depth of mortise ( L )榫头零件
Tenon part材料宽度
Material width ( {W}_{\mathrm{s}} )材料厚度
Material thickness ( {D}_{\mathrm{s}} )三角榫肩厚度
Thickness of
triangular
tenon ( {u}_{1} )榫偏置
Offset of tenon ( {u}_{2} )上下边距
Margin between bottom ( {u}_{3} )后偏置
Back offset ( {u}_{4} )榫头厚
Thickness of tenon ( a )榫头宽
Width of tenon
( b )榫头长
Length of tenon ( l )由于同类型榫卯的拓扑关系通常保持不变,部分位置尺寸参数可由其他位置尺寸参数的函数表达式来替代。
榫眼的左右偏置和下偏置,以及榫头的左右偏置和后偏置,均可通过表达式自动计算出数值,不需要再手动进行参数设置。
榫眼左右边距:
{W}_{3}=0.5\left(G-B\right) (5) 榫眼下偏置(W4):
{W}_{4}={W}_{\mathrm{m}}-{W}_{1}-{W}_{2}-A (6) 榫头上下边距:
{u}_{3}=0.5({W}_{\mathrm{s}}-b) (7) 式中:b为椭圆榫头的宽度。
榫头后偏置(u4):
{u}_{4}={D}_{\mathrm{s}}-{u}_{1}-{u}_{2}-a (8) 式中:Ds为榫头材料断面宽度。
3.3 基于装配约束的榫卯尺寸关联设计
3.3.1 榫卯构件的装配关系分析
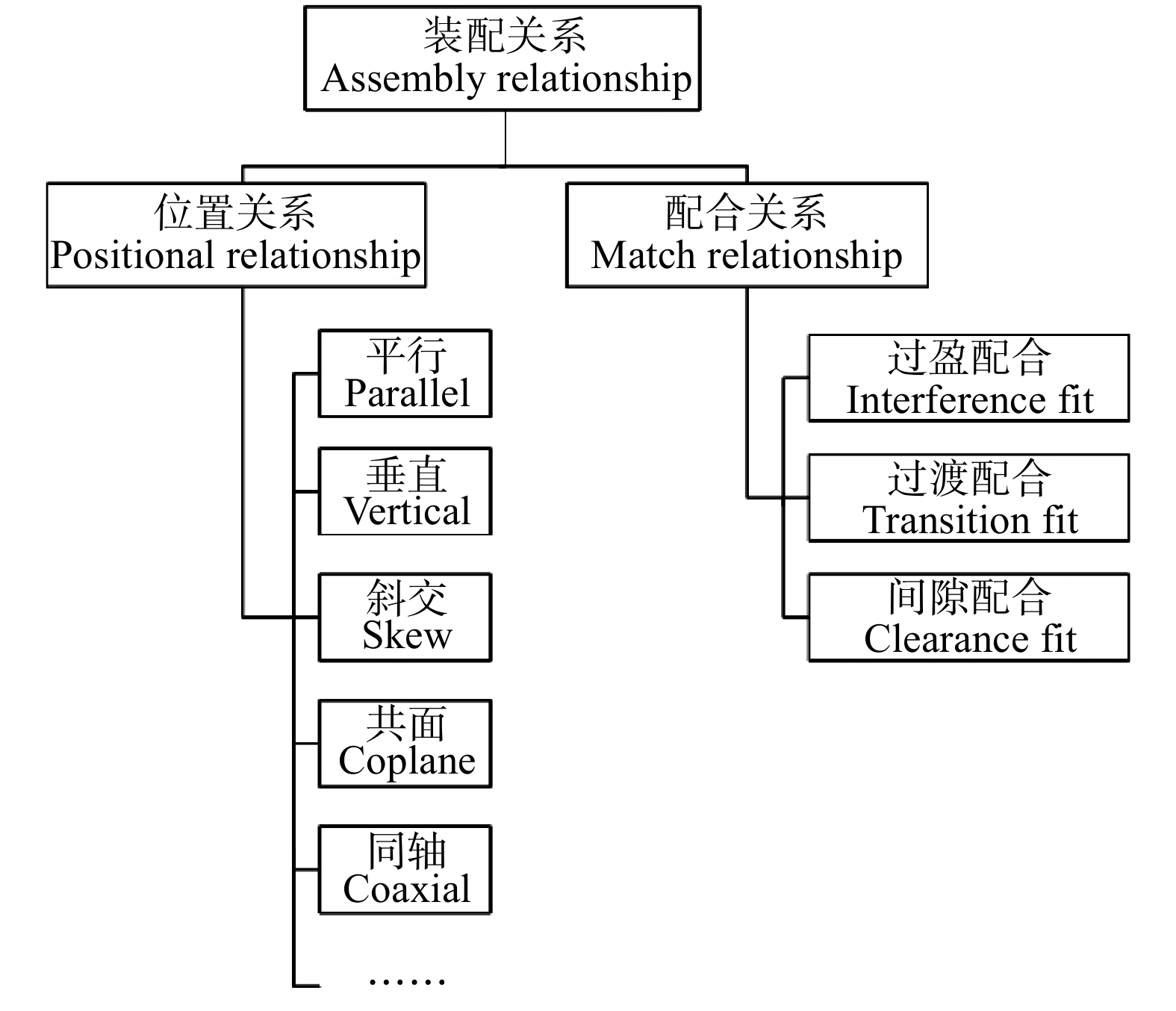
参考机械设计中装配体常见装配关系,结合榫卯配合属于静配合的特点,总结了榫卯的常见装配关系(图4),主要分为位置关系和配合关系两类,位置关系用于约束零件的相对位置,配合关系用于描述榫卯零件间的配合紧密程度[18]。
3.3.2 基于榫卯位置关系的尺寸参数关联设计
位置关系是指特征图素的位置会随着其参照的特征图素的位置改变而发生变化的关联关系[19]。在榫卯中常见的位置关系有平行、垂直、斜交、同轴等,这种信息表明了几何形状间的“隐式”约束关系。
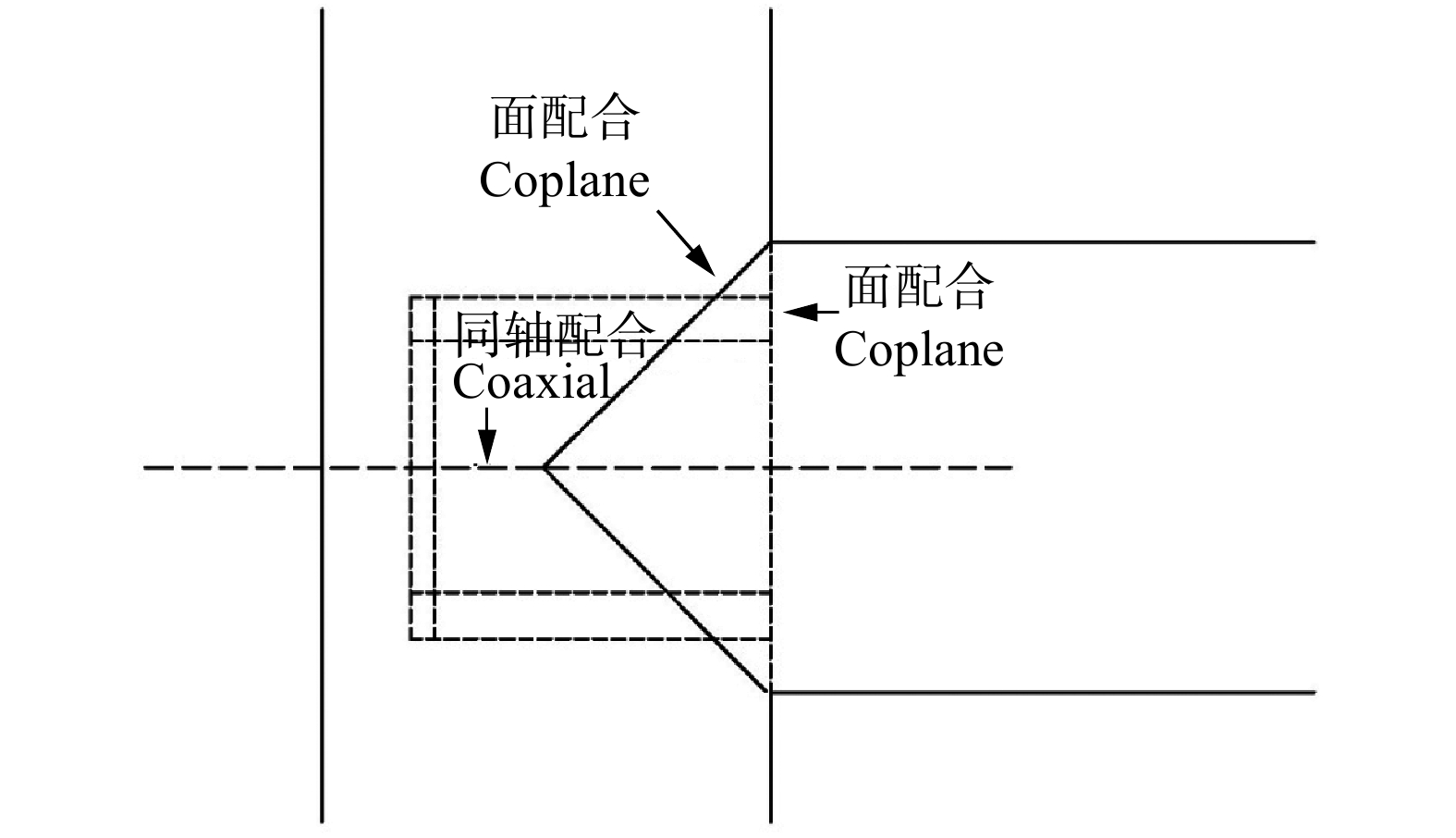
以格肩榫为例,对榫卯装配中存在的位置关系进行了分析,如为格肩榫两个零件的位置配合,装配关系包括两个面配合和一个同轴配合(图5)。其中面配合起到了对装配定位的作用,同轴配合不仅有装配定位的作用,还起到了确定榫头榫眼配合关系的作用。
根据图5中得到的格肩榫位置配合关系的分析,结合表1,可得出如下结论,并建立数学模型。
面配合处,三角格肩与三角肩缺完全重合,且大小一致,可得:
G={W}_{\mathrm{s}} (9) {W}_{1}={u}_{1} (10) 榫头与榫眼之间同轴装配,榫头最长不能突出于材料之外,可得:
l\leqslant {D}_{\mathrm{m}} (11) 从提高榫卯结构强度的方面考虑,榫头长度应尽可能取最大值。但根据调研,现有很多企业为了家具美观,多采用闷榫形式,因而在加工榫眼时,一般会保留2 mm的深度不挖穿,也即:
L= { D}_{\mathrm{m}}-2 (12) 因此,只要确定了榫头材料断面宽度Ws、榫眼边距W1(三角肩缺厚度)、榫眼材料断面厚度Dm,就可以通过关联函数确定三角肩缺的底边长G、榫眼深度L和榫边距u1(三角榫肩厚度),不需要再进行额外的参数值设定。
3.3.3 基于榫卯配合关系的尺寸参数关联设计
榫卯中常见的配合关系主要分为过盈配合、过渡配合和间隙配合,配合关系定义了零件间配合的紧密程度。榫卯的配合关系与榫卯材料属性、榫卯配合方向和木纹走向均有关联[20]。
将榫头厚度方向配合参数描述为参数ΔA,榫头宽度方向配合参数描述为参数ΔB,榫头长度方向配合参数描述为参数ΔL。
由于木材力学性质存在着各向异性,顺纹抗拉强度远高于横纹抗拉强度,在实际加工时,通常使榫眼的长度方向与木材纤维方向基本一致,此时,对榫头厚度方向取间隙或过渡配合,即ΔA ≤ 0;榫头宽度方向取过盈或过渡配合,即ΔB ≥ 0;为了防止榫头过长而导致配合面无法完全贴合的情况发生,榫头长度方向通常采用−2 mm的间隙配合,因此ΔL可设置系统预设值为−2 mm。
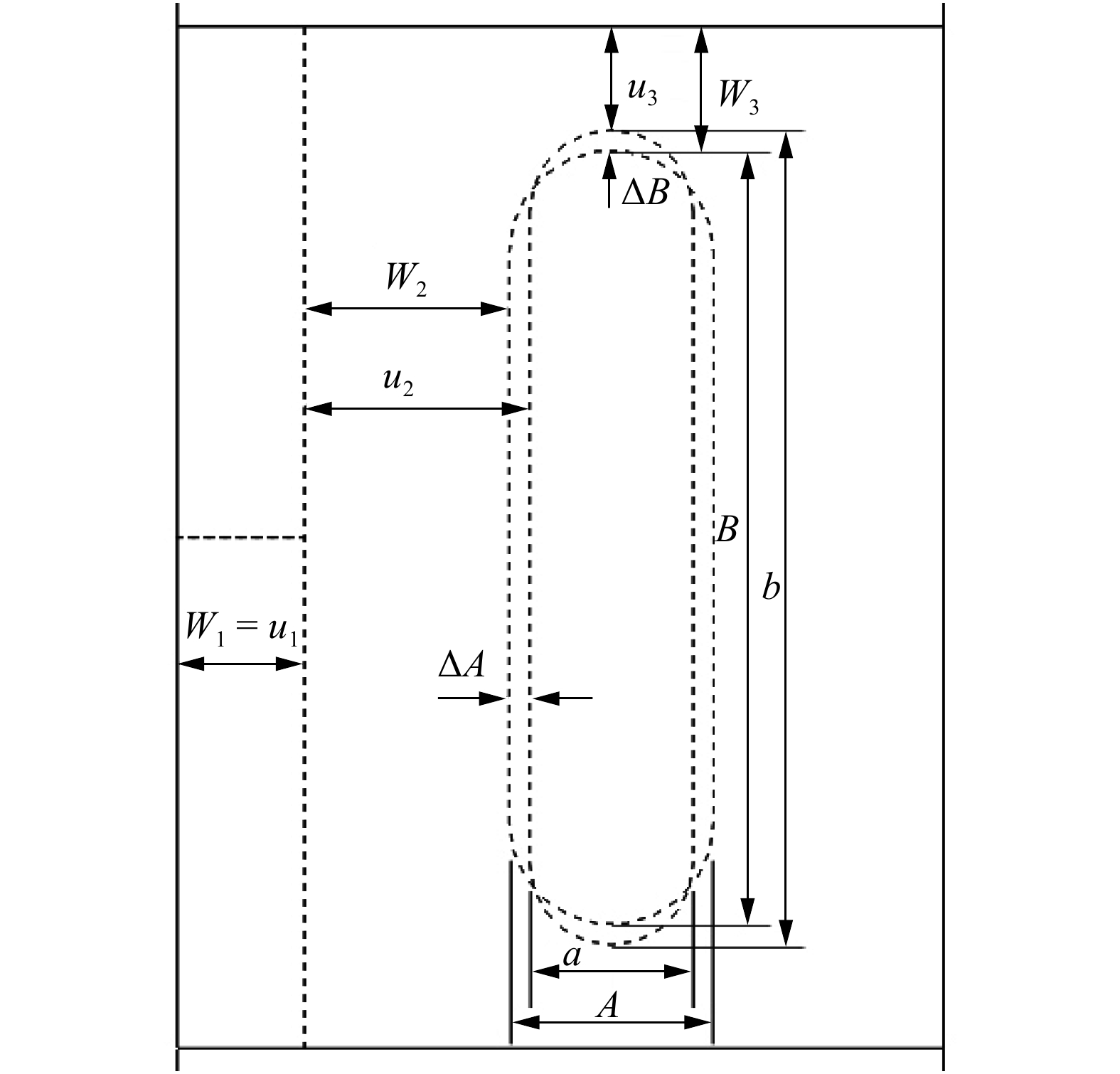
图6为格肩榫配合关系和关联尺寸参数的示意图,根据榫卯的配合关系,建立榫头与榫眼尺寸参数的配合关联关系:
![]() 图 6 格肩榫配合关系和关联尺寸参数A为榫眼宽度,B为榫眼长度,L为榫眼深度,a为榫头厚度,b为榫头宽度,l为榫头长度,ΔA为榫头厚度方向配合参数,ΔB为榫头宽度方向配合参数,ΔL为榫头长度方向配合参数。A is the width of mortise,B is the length of mortise,L is the depth of mortise,a is the thickness of tenon, b is the width of tenon,l is the length of mortise, ΔA is the fitting parameter of the thickness of mortise,ΔB is the fitting parameter of the width of mortise, and ΔL is the fitting parameter of the length of mortise.Figure 6. Matching relationship and related dimension parameters of lattice shoulder tenon
图 6 格肩榫配合关系和关联尺寸参数A为榫眼宽度,B为榫眼长度,L为榫眼深度,a为榫头厚度,b为榫头宽度,l为榫头长度,ΔA为榫头厚度方向配合参数,ΔB为榫头宽度方向配合参数,ΔL为榫头长度方向配合参数。A is the width of mortise,B is the length of mortise,L is the depth of mortise,a is the thickness of tenon, b is the width of tenon,l is the length of mortise, ΔA is the fitting parameter of the thickness of mortise,ΔB is the fitting parameter of the width of mortise, and ΔL is the fitting parameter of the length of mortise.Figure 6. Matching relationship and related dimension parameters of lattice shoulder tenonA=a+\mathrm{\Delta }A (13) B=b+\mathrm{\Delta }B (14) L=l+\mathrm{\Delta }L (15) 式中:ΔA为榫头厚度方向配合参数,ΔB为榫头宽度方向配合参数,ΔL为榫头长度方向配合参数。
因此只要确定了榫眼的宽度A、高度B、深度L,就可以由配合关系计算得出榫头的厚度a、宽度b和长度l,不需要再手动设定榫头尺寸参数值。
综合配合关系和榫头榫眼同轴装配位置关系,又可得到如下关联函数:
{u}_{2}={W}_{2}- 0.5 \mathrm{\Delta }A (16) {u}_{3}={W}_{3}- 0.5 \mathrm{\Delta }B (17) 根据式(16)、(17)的关联函数,当榫头偏置u2和榫头上下边距u3以及配合参数
ΔA和ΔB,就可以通过关联函数自动确定榫眼偏置W2和榫眼左右边距W3,不需要再进行额外的参数值设定。 近些年来,关于榫卯配合和材料属性关系的研究较多[21-22],因而,可根据以往的理论研究结果,建立榫卯配合参数值(即参数ΔA和ΔB)与常见木材属性的映射关系,并构建配合参数库。根据配合参数库,用户只需要选择材料属性,系统自动从参数库中匹配对应参数ΔA和ΔB推荐值,如果能匹配到,则自动生成预设值并对配合尺寸参数进行赋值,预设值可修改。配合参数库可根据用户实际需求,不断扩充。
3.4 基于工艺约束的榫卯尺寸关联设计及优化
榫卯制作工艺在漫长发展过程中,积累了大量的工艺知识。这些知识是实现智能化生产所必须的,但却掌握在少数工艺设计人员手中,更缺乏一种有效的知识表达和组织形式。一旦原岗位的技术人员离开,就会造成工艺数据的缺失。在实际生产中,新榫型尺寸和工艺参数的确定及优化主要依靠反复的试加工摸索,这种方式带来了人力物力的浪费。因此,选取一种合理有效,且能被计算机识别的方式对工艺知识进行描述和存储,对实现工艺知识重用,优化榫卯结构显得尤为重要。
本研究将把榫卯工艺知识分为加工方式,市场调研、工艺记录3个类,依次建立其与榫卯尺寸参数的关联函数,进而组建榫卯尺寸参数与工艺关系的集合,用于优化榫卯尺寸参数的设置。
3.4.1 数控加工方式对榫卯零件尺寸约束的分析
榫卯的结构必然受到加工方式的影响,由于数控加工榫卯已经成为主流和势,数控加工的工具又为数控刀具,因而其尺寸必然受到数控刀具尺寸的约束[23]。例如,改良型格肩榫,就必须满足榫孔宽度不小于铣刀直径(d),榫头偏置不小于下刀直径,否则刀具将无法进刀进行加工。该约束关系可以描述为:
({A}\geqslant d)\cap {(u}_{2}\geqslant d) (18) 3.4.2 基于市场调研的榫卯尺寸参数范围的设定
通过对南通、苏州、广东等地家具企业的调研,以及部分中式榫卯做法相关文献资料[24-25]的统计,共调研了112件中式家具,其中椅凳类家具46件,桌案类家具21件,箱柜类家具28件,床榻类家具3件,其他类家具4件;统计并测量了部分榫卯结构的尺寸和使用频率,其中格肩榫108组。根据统计结果,对格肩榫尺寸参数的取值范围和部分结构尺寸参数的最常见取值进行整理,具体结果见表2。
表 2 格肩榫常见尺寸范围Table 2. Common size range of lattice shoulder tenon零件名称 Component name 尺寸类型 Dimension type 尺寸范围 Range of size/mm 常用尺寸 Commonly used size/mm 材料尺寸 Material size {W}_{\mathrm{m}} , {W}_{\mathrm{s}} 13 ~ 74 24、30、32、42 {D}_{\mathrm{m}} , {D}_{\mathrm{s}} 9 ~ 65 28、30、35、42 格肩 Lattice shoulder {u}_{1}, {W}_{1} 4 ~ 12,以5 ~ 8内居多
4−12,far more prevalent in 5−86 榫头尺寸 Tenon size a 4 ~ 13,以6 ~ 8内居多
4−13,far more prevalent 6−86、7、8 b 13 ~ 74 28、32、33 u2 6 ~ 8 8 注:调研对象为108组格肩榫。Note: 108 groups of lattice shoulder tenons are investigated. 根据表格内容,可将这些格肩榫尺寸的常见取值范围描述为:
\left\{ {\begin{aligned} & {13 \leqslant {W_{\rm{s}}} \leqslant 74}\\ & {9 \leqslant {D_{\rm{s}}} \leqslant 65}\\ & {4 \leqslant a \leqslant 13}\\ & {13 \leqslant b \leqslant 74}\\ & {4 \leqslant {W_1} \leqslant 12} \end{aligned}} \right. (19) 根据调研结果,榫肩厚度u1常见参数值为6 mm,因此,可为W1/
{u}_{1} 设置系统预设值为6 mm;另外,根据家具企业实地调研,发现企业生产中最常用直径为8 mm的立铣刀加工榫头榫眼,即d = 8 mm,同时为了方便高效加工,通常取榫头偏置等于铣刀直径,因此u2 = d。同时,为了便于加工椭圆榫头,也为了使椭圆榫头宽度达到最大,一部分企业将榫头上下边距u3设置为0.5 mm。根据以上调研结论,可得出以下参数约束关系:{W_1}{\rm{}} = {u_1} = 6 (20) {u_2} = d = {\rm{ }}8 (21) {u_3} = 0.5 (22) b = W_{\rm{s}}-2{u_3} = W_{\rm{s}}-1 (23) 这些常用值均采用系统预设值的方式预先填入尺寸参数数据框中,既起到了给出参考值的作用,也减少了用户需手动输入的参数数量。系统允许用户修改预设值,但自定义的参数值必须在调研得到的尺寸参数取值范围内。
3.4.3 基于工艺知识的榫卯尺寸参数优化
工艺知识优化管理的方法主要有3种:专家系统、数据库、数学模型[26]。专家系统就是以专家观点作为工艺规则;数据库方法就是将各种工艺数据形成数据库,通过数据库系统来实现工艺参数的管理;数学模型的方法则是将用数学方法推导各种优化公式,利用各种优化理论实现优化[27]。本文主要采用数学模型的方法,参照工艺知识本体定义,将原先分散的工艺知识统一用关联函数的形式进行替换,再用可被计算机识别的约束语句和表达式,就可以转化为内部计算信息,对榫卯尺寸参数也形成一定的约束,起到进一步优化参数的作用。
表3为部分榫卯工艺知识及等价关联函数,当用户不选用系统预设值,自定义参数值时,系统会根据这些逻辑判断语言,对自定义参数值进行判断。当自定义参数值不合理时,系统给出修改提示,起到合理配置榫卯尺寸参数和榫卯结构形式的作用。
表 3 部分榫卯尺寸的工艺知识和等价关联函数Table 3. Technological knowledge and equal dependent function of mortise and tenon joint工艺知识
Process knowledge等价关联函数
Equivalent correlation function备注
Remark欠榫负拉力
A short tenon takes less strainl ≥ Dm/2 l为榫头长度,Dm 为榫眼厚度
l is the mortise length, and Dm is the thickness of mortise material强卯弱榫
Strong tenon and weak mortiseDm/4 ≤ A ≤ Dm/3.5 A为榫眼宽度
A is the tenon width小格肩肩高居半则蠢
Small lattice shoulder height is less than half width of materialh ≤ 0.5Dm,推荐值h = Dm/3
When h ≤ 0.5Dm, recommended value h = Dm/3h为小格肩肩高
h is the small lattice shoulder height边距厚以5 ~ 6 mm为宜
Recommended value of margin thickness is 5−6 mmW1 = 5 mm \cup W1 = 6 mm W1为榫边距
W1 is the margin thickness平分双榫抗力更强
Double tenon structure has stronger tensile forcea ≥ 25 mm,推荐双榫结构;b ≥ 40 mm,推荐双榫结构
If a ≥ 25 mm, double tenon structure is recommended; if b ≥ 40 mm, double tenon structure is recommendeda为榫头厚度,b为榫头宽度
a is tenon thickness, and b is tenon width3.5 基于综合约束的榫卯尺寸智能化确定
为了便于说明问题,本文作了如下定义:将榫卯零件材料断面尺寸称为用户输入参数;将由系统给出可修改预设值的尺寸参数称为预设参数;被其他用户输入参数和预设参数驱动的尺寸参数称为因变参数。
以格肩榫为例,首先分别从装配关系约束和工艺约束两个方面入手,建立了榫卯尺寸参数的多种关联函数;最后综合装配关系约束和工艺约束这两方面的约束关系,在式(1) ~ (23)关联函数的基础上,创建了如表4所示的格角榫的关联参数函数关系表。其中,Ws、Wm、Ds、Dm、Lm等断面尺寸为用户必须要手动输入的参数,预设参数由系统提供可人工进行修改的预设值,因变参数则由系统根据关联函数和端面尺寸及预设值,自动计算并填入相应参数框。
表 4 榫卯尺寸参数关联函数表(以格肩榫为例)Table 4. Relevant function table of dimension parameters (taking lattice shoulder tenon for an example)参数类型
Parameter type参数名
Parameter name取值范围或系统内部预设值
Value range and preset value/mm用户输入参数
Input parameter from userWs, Wm, Ds, Dm 13 ≤ Ws ≤ 74,13 ≤ Wm ≤ 74,9 ≤ Ds ≤ 65,9 ≤ Dm ≤ 65 Lm 榫眼中心距端头距离的设计值
Design value of the distance between middle of tenon and end预设参数(系统允许用户修改预设值)
Preset value (system allows users to
modify the default value)W1 W1 = 6,4 ≤ W1 ≤ 12 u2 u2 = 8 u3 u3 = 0.5 A A = 8 ΔA 榫头厚度方向上配合参数库
Library of fit parameter in the mortise thickness directionΔB 榫头宽度方向上配合参数库
Library of fit parameter in the mortise width directionΔL ΔL = −2 因变参数
Dependent parameterG G = Ws B B = Ws – 1 – 0.5ΔB L L= Dm – 2 u1 u1= W1 W2 W2 = u2 + 0.5ΔA a a = A – ΔA,4 ≤ a ≤ 13 b B = B – ΔB,13 ≤ b ≤ 74 l l = L – ΔL W3 W3 = u3 + 0.5ΔB W4 W4 = Wm – W1 – W2 – A u4 u4 = Ds – u1 – u2 – a 关联参数函数表就是榫卯尺寸参数传递的桥梁,各榫卯装配体内部各参数通过关联函数,实现数据传递。只需要对榫卯零件的断面尺寸进行参数设置,结合系统给出的部分参数预设值,系统会更根据参数关联函数表中的关联函数对因变参数逐一进行计算并输出参数值。当用户修改预设值时,系统又会根据存储的参数取值范围及工艺知识,对参数进行检验。将参数函数表以可被计算机识别的形式进行存储,就形成了基于综合约束的榫卯尺寸智能化确定方法。
其他榫卯尺寸的智能化确定也可以采用同样的方法。
4. 结 论
利用参数化设计思想,取格肩榫为例,以零件的断面尺寸为输入参数,分别从榫卯的装配和工艺两方面,进行了榫卯尺寸关联设计研究;在此基础上,综合装配和工艺两方面的约束,确定了榫卯尺寸智能化确定的方法。为实现榫卯,乃至实木加工的智能制造,提供了基础条件。主要研究结果如下:
(1)完成了基于装配约束的榫卯尺寸确定:建立榫卯数学模型,提取榫卯尺寸并进行分类,再基于榫卯位置和配合两方面的配合关系,进行了榫卯尺寸的关联设计。
(2)从数控加工方式与尺寸约束、市场调研与尺寸参数范围设定、工艺知识优化尺寸参数3个方面完成了基于工艺约束的榫卯尺寸确定。
(3)综合装配和工艺两方面与榫卯尺寸的关联,创建了一个以榫卯尺寸参数为基础的关联参数函数表,实现了榫卯尺寸的智能化确定。
-
图 2 格肩榫榫眼零件的几何模型
Wm为榫眼材料断面宽度;Dm为榫眼材料断面厚度;Lm为榫眼中心距离端面在X方向位置;G为三角肩缺底边长度;A为椭圆榫眼的宽度;B为椭圆榫眼的长度;L为椭圆榫眼的深度;W1为三角肩缺的厚度;W2为榫眼偏置(三角肩缺下边线与椭圆榫眼上边线的距离);W3为椭圆榫眼左右边距;W4为榫眼下偏置(椭圆榫眼下边线于材料底面间的距离)。Wm is the width of mortise material, Dm is the thickness of mortise material, Lm is the distance between the center of mortise and the end face in X direction, G is the length of breach, A is the wide of mortise, B is the length of mortise, L is the depth of mortise, W1 is the thickness of triangular mortise, W2 is the offset of mortise (distance between the border-bottom of triangular mortise and border-top of mortise), W3 is the margins of mortise, and W4 is the under offset of mortise (distance between the border-bottom of mortise and the underside of material).
Figure 2. Geometrical model of modified lattice shoulder mortise
图 3 格肩榫榫头零件的几何模型
Ws为榫头材料断面宽度;Ds为榫头材料断面厚度; {L}_{\mathrm{s}} 为材料端面到榫头底面的距离;a为椭圆榫头的厚度;b为椭圆榫头的宽度;l为椭圆榫头的长度;u1为三角榫肩厚度;u2为榫头偏置;u3为椭圆榫头上下边距。Ws is the width of joint material, Ds is the thickness of joint material, Ls is the distance between the end face and the bottom of tenon, a is the thickness of tenon, b is the width of tenon, l is the length of tenon, u1 is the thickness of triangular tenon, u2 is the offset of tenon, and u3 is the margins of tenon.
Figure 3. Geometrical model of modified lattice shoulder tenon
图 6 格肩榫配合关系和关联尺寸参数
A为榫眼宽度,B为榫眼长度,L为榫眼深度,a为榫头厚度,b为榫头宽度,l为榫头长度,ΔA为榫头厚度方向配合参数,ΔB为榫头宽度方向配合参数,ΔL为榫头长度方向配合参数。A is the width of mortise,B is the length of mortise,L is the depth of mortise,a is the thickness of tenon, b is the width of tenon,l is the length of mortise, ΔA is the fitting parameter of the thickness of mortise,ΔB is the fitting parameter of the width of mortise, and ΔL is the fitting parameter of the length of mortise.
Figure 6. Matching relationship and related dimension parameters of lattice shoulder tenon
表 1 格肩榫的参数表
Table 1 Parameter lists of lattice shoulder tenon
零件名称
Component name断面尺寸参数
Cross-section dimension parameter位置尺寸参数
Location dimension parameter形状尺寸参数
Form size parameter榫眼零件
Mortise part材料宽度
Material width{(W}_{\mathrm{m}}) 材料厚度
Material thickness ({D}_{\mathrm{m}} )榫眼位置
Location of mortise ({L}_{\mathrm{m}} )三角肩缺厚度
Thickness of
triangular mortise ({W}_{1} )榫偏置
Offset of mortise ({W}_{2} )左右边距
Margin between bottom ({W}_{3} )下偏置
Under offset ({W}_{4} )肩缺底长
Length of breach (G )榫眼宽
Width of mortise (A )榫眼长
Length of mortise (B )榫眼深
Depth of mortise (L )榫头零件
Tenon part材料宽度
Material width ({W}_{\mathrm{s}} )材料厚度
Material thickness ({D}_{\mathrm{s}} )三角榫肩厚度
Thickness of
triangular
tenon ({u}_{1} )榫偏置
Offset of tenon ({u}_{2} )上下边距
Margin between bottom ({u}_{3} )后偏置
Back offset ({u}_{4} )榫头厚
Thickness of tenon (a )榫头宽
Width of tenon
(b )榫头长
Length of tenon (l )表 2 格肩榫常见尺寸范围
Table 2 Common size range of lattice shoulder tenon
零件名称 Component name 尺寸类型 Dimension type 尺寸范围 Range of size/mm 常用尺寸 Commonly used size/mm 材料尺寸 Material size {W}_{\mathrm{m}} ,{W}_{\mathrm{s}} 13 ~ 74 24、30、32、42 {D}_{\mathrm{m}} ,{D}_{\mathrm{s}} 9 ~ 65 28、30、35、42 格肩 Lattice shoulder {u}_{1} ,{W}_{1} 4 ~ 12,以5 ~ 8内居多
4−12,far more prevalent in 5−86 榫头尺寸 Tenon size a 4 ~ 13,以6 ~ 8内居多
4−13,far more prevalent 6−86、7、8 b 13 ~ 74 28、32、33 u2 6 ~ 8 8 注:调研对象为108组格肩榫。Note: 108 groups of lattice shoulder tenons are investigated. 表 3 部分榫卯尺寸的工艺知识和等价关联函数
Table 3 Technological knowledge and equal dependent function of mortise and tenon joint
工艺知识
Process knowledge等价关联函数
Equivalent correlation function备注
Remark欠榫负拉力
A short tenon takes less strainl ≥ Dm/2 l为榫头长度,Dm 为榫眼厚度
l is the mortise length, and Dm is the thickness of mortise material强卯弱榫
Strong tenon and weak mortiseDm/4 ≤ A ≤ Dm/3.5 A为榫眼宽度
A is the tenon width小格肩肩高居半则蠢
Small lattice shoulder height is less than half width of materialh ≤ 0.5Dm,推荐值h = Dm/3
When h ≤ 0.5Dm, recommended value h = Dm/3h为小格肩肩高
h is the small lattice shoulder height边距厚以5 ~ 6 mm为宜
Recommended value of margin thickness is 5−6 mmW1 = 5 mm \cup W1 = 6 mmW1为榫边距
W1 is the margin thickness平分双榫抗力更强
Double tenon structure has stronger tensile forcea ≥ 25 mm,推荐双榫结构;b ≥ 40 mm,推荐双榫结构
If a ≥ 25 mm, double tenon structure is recommended; if b ≥ 40 mm, double tenon structure is recommendeda为榫头厚度,b为榫头宽度
a is tenon thickness, and b is tenon width表 4 榫卯尺寸参数关联函数表(以格肩榫为例)
Table 4 Relevant function table of dimension parameters (taking lattice shoulder tenon for an example)
参数类型
Parameter type参数名
Parameter name取值范围或系统内部预设值
Value range and preset value/mm用户输入参数
Input parameter from userWs, Wm, Ds, Dm 13 ≤ Ws ≤ 74,13 ≤ Wm ≤ 74,9 ≤ Ds ≤ 65,9 ≤ Dm ≤ 65 Lm 榫眼中心距端头距离的设计值
Design value of the distance between middle of tenon and end预设参数(系统允许用户修改预设值)
Preset value (system allows users to
modify the default value)W1 W1 = 6,4 ≤ W1 ≤ 12 u2 u2 = 8 u3 u3 = 0.5 A A = 8 ΔA 榫头厚度方向上配合参数库
Library of fit parameter in the mortise thickness directionΔB 榫头宽度方向上配合参数库
Library of fit parameter in the mortise width directionΔL ΔL = −2 因变参数
Dependent parameterG G = Ws B B = Ws – 1 – 0.5ΔB L L= Dm – 2 u1 u1= W1 W2 W2 = u2 + 0.5ΔA a a = A – ΔA,4 ≤ a ≤ 13 b B = B – ΔB,13 ≤ b ≤ 74 l l = L – ΔL W3 W3 = u3 + 0.5ΔB W4 W4 = Wm – W1 – W2 – A u4 u4 = Ds – u1 – u2 – a -
[1] 严婕. 数控加工机床与加工中心在家具制造业中的应用[J]. 林业机械与木工设备, 2014, 24(6):56−57. doi: 10.3969/j.issn.2095-2953.2014.06.023. Yan J. Application of CNC machining lathes and machining centers in the furniture manufacturing industry[J]. Forestry Machinery & Woodworking Equipment, 2014, 24(6): 56−57. doi: 10.3969/j.issn.2095-2953.2014.06.023.
[2] Podskarbi M, Smardzewski J, Moliński K, et al. Design methodology of new furniture joints[J]. Drvna Industrija, 2017, 67(4): 371−380. doi: 10.5552/drind.2016.1622
[3] 唐立华, 杨元. 艺术生态视野下明清家具艺术的衍生传承研究[J]. 家具与室内装饰, 2019(11):14−15. Tang L H, Yang Y. Research on inheritance and development of Ming and Qing furniture art from the perspective of art ecology[J]. Furniture & Interior Design, 2019(11): 14−15.
[4] 丁刚, 赵小芳. 运用参数化方法提升数控加工编程的效率[J]. 机电产品开发与创新, 2016, 29(1):101−102. doi: 10.3969/j.issn.1002-6673.2016.01.038. Ding G, Zhao X F. Using the parametric method to improve numerical control machining programming efficiency[J]. Development & Innovation of Machinery & Electrical Products, 2016, 29(1): 101−102. doi: 10.3969/j.issn.1002-6673.2016.01.038.
[5] 张冶, 陈志英. 基于装配约束关系的零部件参数化设计[J]. 机械科学与技术, 2003(5):710−712. doi: 10.3321/j.issn:1003-8728.2003.05.008. Zhang Y, Chen Z Y. Parametric design for aeroengine parts based on assembly constraint relations[J]. Mechanical Science and Technology, 2003(5): 710−712. doi: 10.3321/j.issn:1003-8728.2003.05.008.
[6] 杜宝江, 孟玉杰, 朱晨旗, 等. 飞机标准件号的多级筛选智能匹配技术[J]. 机械设计与研究, 2013, 29(6):43−46. doi: 10.3969/j.issn.1006-2343.2013.06.012 Du B J, Meng Y J, Zhu C Q, et al. The study on multilevel filter with intelligent matching technology for aircraft standard parts[J]. Machine Design and Research, 2013, 29(6): 43−46. doi: 10.3969/j.issn.1006-2343.2013.06.012
[7] 盛步云, 张成雷, 卢其兵, 等. 云制造服务平台供需智能匹配的研究与实现[J]. 计算机集成制造系统, 2015, 21(3):822−830. Sheng B Y, Zhang C L, Lu Q B, et al. Research and implementation of cloud manufacturing service platforms intelligent matching for supply and demand[J]. Computer Integrated Manufacturing Systems, 2015, 21(3): 822−830.
[8] 赵月容. 可重构板式家具生产系统的建模与优化研究[D]. 哈尔滨: 东北林业大学, 2012. Zhao Y R. Research on modeling and optimating of reconfigurable panel furniture manufacturing system[D]. Harbin: Northeast Forestry University, 2012.
[9] 郭飞燕, 刘检华, 邹方, 等. 数字孪生驱动的装配工艺设计现状及关键实现技术研究[J]. 机械工程学报, 2019, 55(17):110−132. doi: 10.3901/JME.2019.17.110. Guo F Y, Liu J H, Zou F, et al. Research on the State-of-art, connotation and key implementation technology of assembly process planning with digital twin[J]. Journal of Mechanical Engineering, 2019, 55(17): 110−132. doi: 10.3901/JME.2019.17.110.
[10] 陈于书, 王帆. 红木家具零件的参数化设计研究[J]. 木材加工机械, 2017, 28(4):11−15. Chen Y S, Wang F. Study of parametric design of parts of mahogany furniture[J]. Wood Processing Machinery, 2017, 28(4): 11−15.
[11] Hagen H, Roller D. Geometric modeling methods and applications[M]. New York: Springer-Verlag, 1991.
[12] 王进荣. 明式桌椅类家具结构研究[D]. 福州: 福建农林大学, 2018. Wang J R. Research on the structure and model of table and chair in Ming-style furniture[D]. Fuzhou: Fujian Agriculture and Forestry University, 2018.
[13] 王风涛. 基于高级几何学复杂建筑形体的生成及建造研究[D]. 北京: 清华大学, 2012. Wang F T. Generating and fabricating of complex architectural form based on advanced geometry[D]. Beijing: Tsinghua University, 2012.
[14] 张胜欢. 基于Solidworks的明式家具三维参数化模型库的研究[D]. 南京: 南京林业大学, 2015. Zhang S H. Research on parametric model library of Ming-style furniture based on solidworks[D]. Nanjing: Nanjing Forestry University, 2015.
[15] 欧长劲, 苏之晓, 李燕. 基于SolidWorks API的参数化设计及智能装配研究[J]. 轻工机械, 2012, 30(5):69−72. doi: 10.3969/j.issn.1005-2895.2012.05.019. Ou C J, Su Z X, Li Y. Parametric design and intelligent assembly research based on SolidWorks API[J]. Light Industry Machinery, 2012, 30(5): 69−72. doi: 10.3969/j.issn.1005-2895.2012.05.019.
[16] 金昊炫. 基于UG的注塑机模板参数化CAD系统的研究和实现[D]. 杭州: 浙江大学, 2003. Jin H X. The research & realization of injection machine moulding board parametric CAD system based on UG[D]. Hangzhou: Zhejiang University, 2003.
[17] Hillyard R C, Braid I C. Analysis of dimensions and tolerances in computer-aided mechanical design[J]. Computer-Aided Design, 1978, 10(3): 161−166. doi: 10.1016/0010-4485(78)90140-9.
[18] 朱云, 申黎明. 面向用户装配的实木家具榫卯结构设计[J]. 林业工程学报, 2018, 3(3):142−148. Zhu Y, Shen L M. Design for user assembly mortise and tenon structure in solid wood furniture[J]. Journal of Forestry Engineering, 2018, 3(3): 142−148.
[19] 贾棋, 高新凯, 罗钟铉, 等. 基于几何关系约束的特征点匹配算法[J]. 计算机辅助设计与图形学学报, 2015, 27(8):1388−1397. doi: 10.3969/j.issn.1003-9775.2015.08.005. Jia Q, Gao X K, Luo Z X, et al. Feature points matching based on geometric constraints[J]. Journal of Computer-Aided Design & Computer Graphics, 2015, 27(8): 1388−1397. doi: 10.3969/j.issn.1003-9775.2015.08.005.
[20] 杨建福. 榫卯结构参数对其力学性能的影响研究[D]. 北京: 北京工业大学, 2017. Yang J F. Effect of parameters on mechanical properties of mortise and tenon structures[D]. Beijing: Beijing University of Technology, 2017.
[21] 钟世禄, 关惠元. 椭圆榫过盈配合量与木材密度的关系[J]. 林业科技开发, 2007(2):57−59. doi: 10.3969/j.issn.1000-8101.2007.02.018. Zhong S L, Guan H Y. Relationship between optimal value of interference fit and wood density in oval tenon joint[J]. Journal of Forestry Engineering, 2007(2): 57−59. doi: 10.3969/j.issn.1000-8101.2007.02.018.
[22] 胡文刚, 白珏, 关惠元. 一种速生材榫接合节点增强方法[J]. 北京林业大学学报, 2017, 39(4):101−107. Hu W G, Bai J, Guan H Y. Investigation on a method of increasing mortise and tenon joint strength of a fast growing wood[J]. Journal of Beijing Forestry University, 2017, 39(4): 101−107.
[23] 赵霞, 陈洋, 殷超. 现代需求与工艺对新中式家具构建影响研究[J]. 设计, 2019, 32(22):122−124. Zhao X, Chen Y, Yin C. Research on the influence of modern demand and craft on the construction of new Chinese style furniture[J]. Design, 2019, 32(22): 122−124.
[24] 李敏, 吴智慧, 毛轶超. 现代红木家具榫卯形式的研究[J]. 包装工程, 2015(4):88−92. Li M, Wu Z H, Mao Y C. The types of mortise and tenon in modern mahogany of furniture[J]. Packaging Engineering, 2015(4): 88−92.
[25] 王世襄. 明式家具研究[M]. 中国香港: 三联书店有限公司, 1989. Wang S X. Ming furniture[M]. Hong Kong: SDX Joint Publishing Company, 1989.
[26] 詹金武, 李涛, 李超. 基于人工智能的TBM选型适应性评价决策支持系统[J]. 煤炭学报, 2019, 44(10):3258−3271. Zhan J W, Li T, Li C. Decision support system of adaptability evaluation for TBM selection based on artificial intelligence[J]. Journal of China Coal Societ, 2019, 44(10): 3258−3271.
[27] 刘红政. 产品设计重用中的创新方法研究[D]. 杭州: 浙江大学, 2008. Liu H Z. Research on innovative method of product design reuse[D]. Hangzhou: Zhejiang University, 2008.
-
期刊类型引用(5)
1. 王国坤,熊先青,杨路洁,徐寅. 面向板式家具数字化制造的拆单软件现状与发展分析. 林业工程学报. 2024(03): 175-183 .  百度学术
百度学术
2. 王华,罗鑫,孙香,唐斌,万川,徐伟. 改良粽角榫的参数化设计方法. 林业工程学报. 2024(03): 168-174 .  百度学术
百度学术
3. 黄利江,李云鹏,宫思明,蔺海,王亮. 基于参数化工艺模板的智能工艺设计. 机床与液压. 2023(18): 84-89 .  百度学术
百度学术
4. 何守旺. 铁路隧道TBM衬砌断面辅助设计系统设计与实现. 铁道标准设计. 2022(08): 132-137 .  百度学术
百度学术
5. 王钟箐,路峻,吴启红. 基于装配式的古建筑榫卯库的参数化构建. 成都大学学报(自然科学版). 2021(04): 440-446 .  百度学术
百度学术
其他类型引用(0)




 下载:
下载: