Effects of Cd-Zn combined stress on chemical defense of Populus alba ‘Berolinensis’
-
摘要:目的探究镉（Cd）、锌（Zn）复合胁迫对银中杨化学防御的影响。方法本实验将3种含量的Cd（0.5、1.5、2.5 mg/kg）和Zn（300、500、700 mg/kg），采用正交实验设计（3 × 3）分别复合施加到1年生银中杨生长的土壤中，在胁迫30、40和50 d后，分析各组银中杨叶片中的防御蛋白活性以及次生代谢物质的含量。结果在Cd、Zn复合胁迫下，银中杨叶片中防御蛋白活性以及次生代谢物质的含量均随Cd和Zn含量的增加而降低，且高含量Cd、Zn复合胁迫下的防御蛋白的活性和次生代谢物质的含量均显著低于中低含量复合胁迫（P < 0.05）。其中，在Cd、Zn中高含量复合胁迫下，30、40和50 d后，苯丙氨酸解氨酶（PAL）、多酚氧化酶（PPO）、胰蛋白酶抑制剂（TI）、胰凝乳蛋白酶抑制剂（CI）活性、黄酮和木质素含量，与对照组差异显著（P < 0.05）；在Cd、Zn低含量复合胁迫下，30、40 d后的黄酮含量以及50 d后的PAL活性，也显著低于对照组（P < 0.05）。结论Cd和Zn复合胁迫会抑制银中杨叶片内的化学防御水平，且抑制效果呈一定的浓度和时间效应。Abstract:ObjectiveThis study aims to investigate the effects of Cd-Zn combined stress on chemical defense of Populus alba ‘Berolinensis ’ (PAB).MethodThree concentrations of Cd (0.5, 1.5 and 2.5 mg/kg) and Zn (300, 500 and 700 mg/kg) were combined and applied in an orthogonal experimental design (3 × 3) into the soil with one-year-old PAB seedlings. The activities of defense proteins and the contents of secondary metabolites in the PAB leaves were analyzed at 30, 40 and 50 days after Cd-Zn applications, respectively.ResultThe results showed that both the activities of defense proteins and the contents of secondary metabolites in the leaves of PAB seedlings decreased with the increase of Cd-Zn concentrations. Both parameters were significantly lower under the high Cd-Zn stresses than those under the medium-low Cd-Zn stresses (P < 0.05). The activities of PAL, PPO, TI, CI, and the contents of flavonoids and lignin in the PAB leaves under the high-medium Cd-Zn (combined) stresses were significantly lower than those of control (P < 0.05) for all three sampling dates (30, 40 and 50 days after the Cd-Zn application). Under the low Cd-Zn combined stresses, the flavonoid contents at 30 and 40 days after the Cd-Zn application and the PAL activity at 50 days after the Cd-Zn application were also significantly lower than those of control (P < 0.05).ConclusionThe above results illustrate that Cd-Zn combined stress could inhibit the chemical defense levels of the PAB leaves, and such inhibitory effects vary, to certain degrees, with Cd-Zn concentrations and exposure durations. Further studies are need to determine how the Cd-Zn combined stresses affect PAB defoliators.
-
Keywords:
- combined heavy metal stress /
- Populus alba ‘Berolinensis’ /
- Cd /
- Zn /
- chemical defense
-
以林场或县（后文统一称林场）森林资源总体为调查对象，及时、准确地调查监测总体平均每公顷蓄积量（mean stock volume density，MSVD），对上级（如市、省）部门开展森林资源宏观管理、生态保护价值评价、森林碳储量计量、领导干部任期绩效考核等工作都有重要支撑作用[1]。现有的森林资源一类、二类调查为实现林场总体MSVD估计提供了工作基础和数据基础[2-4]，但并不能满足当前对林场森林资源实现年度或按需监测（在二类调查的间隔期内任何一个年度完成调查）的国家需求。一类调查所依赖的系统抽样固定样地数据以省为总体设计，用于省、国家级总体出数可达到足够精度[5]，但若以林场为总体，只依赖一类调查固定样地无法达到精度要求。二类调查通过对每个小班进行角规或标准样地调查等可以得到每个小班的蓄积量，进而汇总计算得到总体MSVD，但这种调查方式工作量很大，通常间隔10年调查一次，不适合年度监测。根据二类调查技术规范[6]，为了控制小班蓄积量调查成果质量，需要通过系统、随机等概率抽样布设抽样样地，通过抽样样地蓄积量估计得到林场总体蓄积量。这是传统的概率抽样调查方法，但要做到年度出数或按需监测，就特别需要更加经济、高效的调查估计方法。而将辅助数据和样地数据综合用于总体参数的估计就是一种常用的方法，且各种遥感数据是最常用的辅助数据[7]。
Ståhl等[8]将森林资源调查方法归纳为4类：概率抽样法（design-based method，DB）、模型辅助法（model-assisted method，MA）、模型法（model-dependent method，MD）和混合法（mixed or hybrid method，HY）。DB依概率从总体单元中抽取样本，根据样本观测值估计总体参数，理论上具有设计无偏性。但由于DB只采用抽样样地数据进行推断，不采用辅助数据，因此在同样抽样精度下需要抽取更多的样本单元[8]。MA本质上属于DB方法，对其改进在于利用辅助数据建立估测模型，用残差校正估测模型的总体参数估计结果，若模型拟合得当，可以提高估计精度，但建立模型所用的样本必需采用概率抽样法获得[9]。MD将样本单元观测值作为因变量，将辅助数据（空间上对总体单元全覆盖）作为自变量，建立回归估测模型（如线性、非线性统计回归模型、各种机器学习模型等），通过辅助变量和估测模型预测每个总体单元的目标参数值，这些值的平均值就为总体参数估计值[10]。HY是指将DB和MD混合应用的方法[11-12]。HY的一种典型应用场景就是当MD方法所用的遥感辅助数据不是对总体全覆盖，而是采用概率抽样方式获取时。这时仍然需要建立一个估测模型，但对总体目标参数估计值的不确定性的估计则需要考虑遥感辅助数据是依概率抽样获取所引起的不确定性。国外已对以上4类方法开展了大量研究，包括对各种方法的比较评价[7-9,13-19]，所涉及的天（卫星）空（航空）地（样地）多源观测数据协同应用模式主要包括：样地−卫星遥感、样地−无/有人机遥感和样地−无/有人机遥感−卫星遥感等。
国内对这4类方法的研究也都有涉及，但很不均衡。DB是国家森林资源调查的基础方法[20]，对其研究较多，如曾伟生等[21]对群团抽样估计效率与群内样地间距的关系进行了研究，对两阶段群团抽样在森林调查中的综合效率进行了讨论；李春干等[22]通过布设抽样遥感样地，通过目视判读确定样地森林资源参数，进而估算总体参数；郑冬梅等[23]对比分析了群团样地判读和图班区划判读的精度，卫星数据采用了资源三号和高分一号数据，验证了两者对森林总体面积估计的差异较小。国内对MA开展研究很少，而且局限于地类面积的成数估计[24-25]，尚未见以遥感作为辅助变量采用MA估计总体蓄积量、平均高等参数的研究。国内森林参数遥感定量估测方向的研究很多[26-30]，所采用的方法绝大多数都属于MD类方法。在HY研究方面，国内主要采用了双重回归估计方法。如宋新民[31]介绍了双重回归抽样法，在方差估计上既考虑了回归估测模型误差，又考虑了抽样误差；针对二类调查业务的HY研究，遥感数据主要以航片为主[32-34]；在宏观监测应用方面，陈振雄等[35]基于遥感大样地双重抽样方法，以遥感样地为一重样本，用于区划判读，地面样地为二重样本，结合遥感样地判读结果，采用双重回归估计法对广东省主要地类面积进行了估计。国内相关研究所涉及的天空地多源数据协同应用模式以样地−卫星遥感、样地−无/有人机遥感为主，采用样地−无人机遥感−卫星遥感模式的较少。目前国内尚未见对现有4类估测方法的比较评价研究。
总之，国际上对区域总体森林参数的估计已形成一套方法体系，合理地利用各种方法将可最大限度发挥天空地多源观测数据协同应用优势，提高林场总体蓄积量的调查监测效率。为了促进新一代遥感技术在我国森林资源调查监测业务中的应用，提高森林资源天空地一体化调查监测技术水平，亟需对现有估测方法进行比较评价研究。
本研究以内蒙古自治区赤峰市喀喇沁旗旺业甸实验林场为研究区，以林场主要人工林的总体MSVD估计为目标，获取了标准样地数据、无人机LiDAR抽样数据，以及对林场全覆盖的Sentinel-2A卫星多光谱遥感数据，对适合以上数据应用的4类5种估测方法进行了比较评价，以期为国内林场总体蓄积量的年度监测提供技术参考。
1. 研究区和数据
1.1 研究区概况
研究区为内蒙古自治区赤峰市喀喇沁旗旺业甸实验林场所覆盖区域（图1），总面积约500 km2，地理坐标为118°09′ ~ 118°30′ E，41°21′ ~ 41°39′N，地势西南高东北低，以中山和低山山地为主，平均海拔800 ~ 1 890 m，年均降水量300 ~ 500 mm，年平均气温4.2 ℃，为大陆季风性气候。土壤类型以草甸土、棕壤、褐土和山地黑土为主。林场的人工林树种以落叶松（Larix gmelinii）、油松（Pinus tabuliformis）、樟子松（Pinus sylvestris）、云杉（Picea asperata）和红松（Pinus koraiensis）为主，天然次生林树种以白桦（Betula platyphylla）、山杨（Populus davidiana）和蒙古栎（Quercus mongolica）为主[36]。
1.2 数据获取与处理
研究所用数据包括卫星遥感数据、无人机LiDAR数据、标准样地数据、无人机CCD数码影像，以及林场的数字化林相图。图2给出了所采用的天空地数据获取方式。卫星遥感数据全覆盖研究区。无人机遥感观测区域和标准样地采用系统抽样方法布设，具体做法为：将研究区划分为22个4 km × 4 km大小的网格，左上角第一个网格的中心点的大地坐标采用随机方式确定，原则上以各网格的中心点作为无人机抽样中心点位置，按照“人”字形状获取3个长方形无人机LiDAR条带数据，3个条带在一端重合，组成一块LiDAR抽样观测数据；再在每个LiDAR抽样块覆盖的人工林内布设4块正方形标准样地，其中1块位于抽样块的中心位置，另外3块位于3个LiDAR条带上，每个条带1块（图2A）。同时还获取了高空间分辨率（0.05 m × 0.05 m）无人机CCD数码相机影像，每个LiDAR抽样块的覆盖范围如图2B所示。
![]()
图 2 无人机和样地数据抽样获取方案示意图Figure 2. Schematic diagram of UAV and sample plot data sampling acquisition scheme1.2.1 卫星遥感数据
卫星数据采用Sentinel-2A（S-2A）多光谱数据，需要2景才能对林场实现全覆盖。这2景数据的成像时间都为2019年10月7日。每景数据包括13个波段，不同波段范围空间分辨率不同，共含10、20和60 m 3种空间分辨率，本研究只采用了其中的10和20 m空间分辨率的多光谱数据，共9个波段（表1）。对每景数据分别进行了辐射定标、大气校正和正射校正等预处理，其中正射校正所需地面控制点的选取参考了正射校正后的无人机CCD数码影像，校正精度在一个像元以内。经以上处理后的S-2A数据的像元大小设为25 m × 25 m（和样地大小一致）；然后对这2景预处理后的数据进行镶嵌处理，进而利用林场矢量边界对镶嵌数据进行裁剪，得到覆盖整个林场的多光谱遥感数据。
表 1 S-2A卫星数据特征Table 1. S-2A satellite data characteristics特征名称
Feature name特征符号
Feature symbol计算公式
Calculation formula特征名称
Feature name特征符号
Feature symbol计算公式
Calculation formula光谱特征
Spectral featureB2、B3、B4、B5、B6、B7、B8a、B11、B12 角二阶矩
Angular second momentAN k∑i,j=1P2i,j 差值植被指数
Difference vegetation indexDVI B8−B4 熵
EntropyEN k∑i,j=1Pi,j(−lnPi,j) 增强植被指数
Enhanced vegetation indexEVI 2.5 × (B8 − B4)/(B8 + 6 × B4 − 7.5 × B2 + 1) 对比度
ContrastCON k∑i,j=1(i−j)2×Pi,j 归一化植被指数
Normalized difference vegetation indexNDVI (B8−B4)/(B8+B4) 均值
MeanME 1k2k∑i,j=1Pi,j 比值植被指数
Ratio vegetation indexSR B8/B4 方差
VarianceVAR k∑i,j=1Pi,j(i,j−ME) 转换归一化植被指数
Transformed normalized difference vegetation indexTNDVI √(B8−B4)/(B8+B4)+0.5 同质性
HomogeneityHOM k∑i,j=1Pi,j1+(i−j)2 叶绿素指数
Chlorophyll indexCIg B8/B3−1 相关性
CorrelationCOR k∑i,j=1P2i,j[(i−ui)−(j−uj)√σ2iσ2j] 反向红边叶绿素指数
Inverted red edge chlorophyll indexIRECI (B7−B4)/(B5/B6) 相异性
DissimilarityDIS k∑i,j=1Pi,j|i−j| 色素简单比值指数
Pigment specific simple ratioPSSRA B7/B4 修正叶绿素吸收反射指数
Modified chlorophyll absorption in reflectance indexMCARI [(B5 − B4) − 0.2 × (B5 − B3)] × (B5/B4) S-2A 红边位置指数
S-2A red edge positionS2REP 705 + 35 × [(B4 + B7)/2 − B5]/(B6 − B5) 修正窄边红边简单比值指数
Modified simple ratio red edge narrowMSRren [(B8a/B5)−1]/√(B8a/B5)+1 红边叶绿素指数
Red edge chlorophyll indexCIgre1 B5/B3−1 红边植被指数
Red edge vegetation indexNDVIre1 (B8−B5)/(B8+B5) CIgre2 B5/B3−1 NDVIre2 (B8−B6)/(B8+B6) CIgre3 B7/B3−1 NDVIre3 (B8−B7)/(B8+B7) 注：B2、B3、B4、B5、B6、B7、B8、B8a、B11、B12代表S-2A数据对应的波段，Pi,j=Di,j/∑ki,j=1Di,j，Di,j为i行j列对应的像元值，k代表计算纹理时窗口大小。Notes: B2, B3, B4, B5, B6, B7, B8, B8a, B11 and B12 represent the bands corresponding to S-2A data; Pi,j=Di,j/∑ki,j=1Di,j, Di,j is the pixel value corresponding to the i row and j column, k represents the window size when calculating the texture. 以S-2A卫星遥感数据为辅助数据建立估测模型时主要考虑了光谱反射率、光谱指数和纹理3类特征，每类包含的具体遥感特征名称、符号和计算公式见表1。纹理特征的计算都采用3 × 3窗口。这34个特征为估测模型建立的备选特征。
由于人力、物力限制，本研究只对优势树种为油松、落叶松和樟子松的人工林进行了样地调查，样地只对林场针叶人工林具有代表性，只适合用于林场针叶人工林总体MSVD的估测。因此林场总体单元只包括优势树种为针叶人工林的小班。采用林场小班矢量数据库中记录的优势树种属性信息，从卫星遥感辅助数据中去除优势树种非针叶人工林的像元，剩下的像元组成林场总体单元集U，包含的总体单元数N为159 535。
1.2.2 无人机数据
2019年9—10月完成了无人机LiDAR条带抽样获取，采用的无人机平台为8轴RC6-2，LiDAR系统为Riegl VUX-1激光雷达系统，飞行高度为58 ~ 340 m。由于空管政策限制，北部3个网格内的数据未能按计划获取，最终只获取了19块无人机LiDAR抽样观测点云数据，平均点云密度为107 ~ 152 pts/m2，垂直精度为−0.36 ~ 0.19 m，水平精度为0.25 m。原始LiDAR点云数据经姿态矫正、噪声点剔除、坐标转换、航带拼接、系统差改正等预处理后，利用TerraSolid软件进行点云分类、去噪以及归一化等处理得到归一化植被点云数据，并对强度信息进行了校正[37]。利用Fusion软件[38]提取常用的高度和强度相关特征参数，主要包括均值、方差、最大值、最小值、标准差、变异系数、四分距差、偏斜度、百分位数等[39]，如表2所示。这些特征的空间分辨率也设为25 m × 25 m。由于无人机飞行区域边界处有数据缺失值问题，将有效区域的边界向内收缩了一部分（图2-A）。无人机有效数据区域内的所有像元构成Sa集合，其中每个像元都和Ｕ的某个单元相对应。Sa包含像元（单元）总数M为11 902。
表 2 LiDAR数据特征Table 2. Feature of LiDAR data特征名称
Feature name特征符号
Feature symbol均值
MeanHmean, Imean 方差和标准差
Variance and standard deviationHvar, Ivar, Hsd, Isd 最大值和最小值
Maximum value and minimum valueHmax, Imax, Hmin, Imin 变异系数
Coefficient of variationHcv, Icv 四分距差
Interquartile distanceHiq, Iiq 偏斜度
SkewnessHsk, Isk 百分位数
PercentileHp05, Hp10, Hp20, Hp25, ···, Hp95, Hp99
Ip05, Ip10, Ip20, Ip25,···, Ip95, Ip99最小高度以上返回点
Count of return point above the minimum heightR1H, R2H,···, R8H, R9H 注：H代表高度，I代表强度，var代表方差，sd代表标准差，max与min分别代表最大值与最小值，cv、iq以及sk分别代表变异系数、四分距差以及偏斜度，p05—p99代表对应的百分位数。Notes: H represents height, I represents intensity, var represents variance, sd represents standard deviation, max and min represent maximum value and minimum value, respectively; cv, iq and sk represent coefficient of variation, interquartile distance and skewness, respectively; p05−p99 represent the corresponding percentiles. 1.2.3 标准样地数据
在获取无人机数据的同时，进行了标准样地调查。样地大小为25 m × 25 m，对样地内胸径大于5 cm的树木进行每木检尺，测量胸径、树高、东西冠幅、南北冠幅及枝下高等参数。为了减少后期遥感影像与样地位置偏差带来的影响，样地位置主要布设在范围较大且均匀的林分中心，样地4个角点位置及样地中心位置采用Zenith15R型GPS-RTK和ZT20型全站仪精确测量，测量精度优于0.15 m。共调查了88块样地，其中76块位于无人机抽样数据块内（图2）。样地优势树种类型包括落叶松、油松和樟子松，有些样地内也会出现少数白桦、黑桦（Betula davurica）等林木。根据表3所列材积计算公式[40]计算样地内所有单木材积，合计得到样地总蓄积量和每公顷蓄积量（蓄积量密度）。所有标准样地蓄积量密度构成样地数据集S，所含样本单元数n为76。
表 3 材积计算公式Table 3. Formula for volume calculation树种 Tree species 材积计算公式 Formula for volume calculation 白桦
Betula platyphyllaV=100.000397507075980248×d2×h+3.8121380807356×10−6×d3×h−0.000843446660194932×d2−0.000290088083727618×d2×h×lgd 黑桦
Betula davuricaV=0.0199215193890509+0.00038814516708027×d2−2.05059660776977×10−5×d2×h−
0.000870310875746131×h2+8.05362136949543×10−5×d×h2落叶松
Larix gmeliniiV=10−3.49890390728004+2.75504846502564×lgd−0.394050839410844×lgd2−1.37915356404294×lgh+1.14586681477751×lgh2 樟子松
Pinus sylvestrisV=0.000445504541007861×d1.66316523786429×exp(0.0989929357004981×h−1.66681646056217/h) 油松
Pinus tabuliformisV=2.53309290763168×10−5×d2×h−8.57378841160325×10−7×d3×h−6.00033429201054×10−5×d2+
2.93720677218884×10−5×d2×h×lgd注：引自文献[40]。V代表单木材积；d代表单木胸径；h代表单木树高。Notes: cited from reference [40]. V represents single tree stock volume, d represents single tree DBH, h represents single tree height. 2. 总体MSVD估计方法和评价指标
2.1 总体MSVD估计方法
以林场针叶人工林为总体，比较评价如下5种方法对总体MSVD的估计效果：
DBp：仅利用样地数据S，采用DB进行估计。这里下标p表示样地。
MDps：利用样地数据S和卫星遥感特征，建立估测模型，模型因变量为标准样地蓄积量密度，自变量为卫星遥感特征。这里，下标ps表示采用的数据包括标准样地蓄积量密度和卫星遥感特征，s表示卫星。
MAps：所用数据和估测模型与MDps相同。与MDps相比，其结果需用标准样地蓄积量密度与对应模型估测结果的残差校正估测模型对总体参数的估计结果。
HYpl：利用样地数据集S和无人机LiDAR遥感特征，用下标pl表示，其中l表示LiDAR；所采用的方法为HY，估测模型以标准样地蓄积量密度为因变量，以LiDAR遥感特征为自变量；和MDps相比，主要区别在总体平均值方差估计上，需要考虑LiDAR数据是按概率抽样获取的，而不是对总体全覆盖。
MDpls：利用了标准样地数据、无人机LiDAR遥感特征和卫星遥感特征；采用分层模型估测法（HMB），这是一种可综合应用天空地数据的估计方法，属于MD类方法。
图3给出了以上5种方法所利用的数据情况。该图最上面表示图例，最下面给出了5种方法的缩写名称，中间是对应每种方法所采用的数据类型，以及各数据类型之间的空间对应关系。
![]()
图 3 各估测方法所利用数据示意图Figure 3. Schematic diagram of the data used by each estimation method2.1.1 DBp
该方法直接采用标准样地数据进行总体均值的估计，根据系统抽样原理，其均值公式如（1）所示[17]。
¯uDB=1n∑i∈Syi (1) 式中：S为样地数据集，
¯uDB 代表总体均值，yi 为样本单元蓄积量密度（样地），n为样本单元数。对于有限总体，系统抽样的均值方差如（2）所示。
V(¯uDB)=1−fn2∑i∈S(yi−¯y)2 (2) 式中：
1−f=N−nN 为有限总体校正系数，¯y 为样本单元均值，N为总体单元数。2.1.2 MDps
该方法利用了全覆盖的卫星遥感特征与标准样地数据，总体均值的估计方程如（3）所示。
{\widehat{\mu }}_{{\mathrm{M}\mathrm{D}}_{\mathrm{p}\mathrm{s}}}={\boldsymbol{\iota }}_{U}^{\mathbf{T}}{\boldsymbol{Z}}_{U}{\widehat{\boldsymbol{\alpha }}}_{S} (3) 式中：
{\widehat{\boldsymbol{\alpha }}}_{{S}} 为模型参数，{\boldsymbol{\iota }}_{U} 为N维向量，每个元素维1/N，{\widehat{\boldsymbol{\alpha }}}_{S}=({{\boldsymbol{Z}}_{S}^{\mathbf{T}}{\boldsymbol{Z}}_{S})}^{-1}{\boldsymbol{Z}}_{S}^{\mathbf{T}}{\boldsymbol{y}}_{S} ，{\boldsymbol{Z}}_{S} 为样地对应的卫星遥感特征，{\boldsymbol{Z}}_{U} 为总体所有单元对应的卫星遥感特征，{\boldsymbol{y}}_{S} 为为样地数据集S的标准样地蓄积量密度。方差估计公式如（4）所示。
\begin{split}\\ V\left({\widehat{\mu }}_{{\mathrm{M}\mathrm{D}}_{\mathrm{p}\mathrm{s}}}\right)={\boldsymbol{\iota }}_{U}^{\mathbf{T}}{\boldsymbol{Z}}_{U}\widehat{\mathrm{C}\mathrm{o}\mathrm{v}}\left({\widehat{\boldsymbol{\alpha }}}_{S}\right){\boldsymbol{Z}}_{U}^{\mathbf{T}}{\boldsymbol{\iota }}_{U} \end{split} (4) 式中：
V\left({\widehat{\mu }}_{{\mathrm{M}\mathrm{D}}_{\mathrm{p}\mathrm{s}}}\right) 为均值方差，\widehat{\mathrm{C}\mathrm{o}\mathrm{v}}\left({\widehat{\boldsymbol{\alpha }}}_{S}\right)= \dfrac{{({\boldsymbol{y}}_{S}-{\boldsymbol{Z}}_{S}{\widehat{\boldsymbol{\alpha }}}_{\boldsymbol{S}})}^{\mathbf{T}}({\boldsymbol{y}}_{S}-{\boldsymbol{Z}}_{S}{\widehat{\boldsymbol{\alpha }}}_{S})}{n-p-1} ({{\boldsymbol{Z}}_{S}^{\mathbf{T}}{\boldsymbol{Z}}_{S})}^{-1} 代表模型参数协方差矩阵，p为遥感特征数[41]。2.1.3 MAps
该方法用MD估计的残差校正估测模型对总体参数的估测值，总体均值计算公式如（5）所示[42]。
{\widehat{\mu }}_{\mathrm{M}\mathrm{A}}=\frac{1}{n}\left({\sum} _{i\in S}{(y}_{i}-{\widehat{y}}_{i})\right) + \frac{1}{N}{\sum} _{i\in U}{\widehat{y}}_{i} (5) 式中：
{\widehat{\mu }}_{\mathrm{M}\mathrm{A}} 为总体均值，{\widehat{y}}_{i} 为i单元对应的估测值；总体均值方差的计算公式如（6）所示。V\left({\widehat{\mu }}_{\mathrm{M}\mathrm{A}}\right)=(1-\frac{n}{N})\frac{1}{n}\frac{1}{n-1}{\sum} _{i\in S}{{(y}_{i}-{\widehat{y}}_{i})}^{2} (6) 式中：
V\left({\widehat{\mu }}_{\mathrm{M}\mathrm{A}}\right) 为均值方差。2.1.4 HYpl
该方法采用地面样地调查数据和采用抽样方法获取的遥感数据估算总体参数[8]。总体均值计算公式如（7）所示[43]。
{\widehat{\mu }}_{\mathrm{H}\mathrm{Y}}={\boldsymbol{\iota }}_{{S}_{{\rm{a}}}}^{\mathbf{T}}{\boldsymbol{X}}_{{S}_{{\rm{a}}}}{\widehat{\boldsymbol{\beta }}}_{S} (7) 式中：Sa为无人机有效数据区域内的所有像元构成的集合。
{\boldsymbol{\iota }}_{{S}_{{\rm{a}}}} 为长度为M的列向量，元素为1/M，M为Sa包含的单元数。{\boldsymbol{X}}_{{S}_{{\rm{a}}}} 为M × （p + 1）的无人机遥感特征，{\widehat{\boldsymbol{\beta }}}_{S}={\left({\boldsymbol{X}}_{S}^{\mathbf{T}}{\boldsymbol{X}}_{S}\right)}^{-1}{\boldsymbol{X}}_{S}^{\mathbf{T}}{\boldsymbol{y}}_{S} ，为标准样地蓄积量密度{\boldsymbol{y}}_{S} 与其对应无人机LiDAR遥感特征{\boldsymbol{X}}_{S} 模拟的线性模型参数。计算方差的公式如（8）所示[15]。
\begin{split} V\left({\widehat{\mu }}_{\mathrm{H}\mathrm{Y}}\right)=&\;\left(1-\frac{M}{N}\right)\frac{1}{M}\frac{1}{M-1}{\sum }_{i=1}^{M}{{\Big(\widehat{y}}_{i}-\overline{\widehat{y}}\Big)}^{2} + \\&\;{\boldsymbol{\iota }}_{{S}_{{\rm{a}}}}^{\mathbf{T}}{\boldsymbol{X}}_{{S}_{{\rm{a}}}}\mathrm{C}\mathrm{o}\mathrm{v}\left({\widehat{\boldsymbol{\beta }}}_{S}\right){\boldsymbol{X}}_{{S}_{{\rm{a}}}}^{\mathbf{T}}{\boldsymbol{\iota }}_{{S}_{{\rm{a}}}} \end{split} (8) 式中：
\mathrm{C}\mathrm{o}\mathrm{v}\left({\widehat{\boldsymbol{\beta }}}_{S}\right)=\widehat{{\sigma }_{e}^{2}}{\left({\boldsymbol{X}}_{S}^{\mathbf{T}}{\boldsymbol{X}}_{S}\right)}^{-1} 为估计参数{\widehat{\boldsymbol{\beta }}}_{S} 的协方差矩阵，\widehat{{\sigma }_{e}^{2}}=\dfrac{{\hat{\boldsymbol{e}}}_{S}^{\mathrm{T}}{\hat{\boldsymbol{e}}}_{S}}{m-p-1} 为估计残差方差，{\hat{\boldsymbol{e}}}_{S}={\boldsymbol{y}}_{S}- {\boldsymbol{X}}_{S}{\hat{\boldsymbol{\beta }}}_{S} ，为样本集S的残差，长度为m的列向量，m为抽样单元数。在异方差的情况下，协方差矩阵\mathrm{C}\mathrm{o}\mathrm{v}\left({\widehat{\boldsymbol{\beta }}}_{S}\right)= {\left({\boldsymbol{X}}_{S}^{\mathbf{T}}{\boldsymbol{X}}_{S}\right)}^{-1}\left[\displaystyle {\sum }_{i=1}^{m}{\hat{e}}_{i}^{2}{{\boldsymbol{x}}}_{i}^{\mathbf{T}}{x}_{i}\right]{\left({\boldsymbol{X}}_{S}^{\mathbf{T}}{\boldsymbol{X}}_{S}\right)}^{-1} ，{{\boldsymbol{x}}}_{i} 为样本集中第i个样本对应的无人机遥感特征，同时，对残差平方{\hat{e}}_{i}^{2} 进行修正，修正参数为\dfrac{m}{m-p-1} [41]。2.1.5 MDpls
Saarela等[7]于2016年提出了分层建模估计方法，该方法综合利用了空天地3种数据源实现参数估算，总体均值的期望值估计公式如（12）所示。
{\widehat{\mu }}_{{\mathrm{M}\mathrm{D}}_{\mathrm{p}\mathrm{l}\mathrm{s}}}={\boldsymbol{\iota }}_{U}^{\mathbf{T}}{\boldsymbol{Z}}_{U}{\left({\boldsymbol{Z}}_{{S}_{\rm{a}}}^{\mathbf{T}}{\boldsymbol{Z}}_{{S}_{\rm{a}}}\right)}^{-1}{\boldsymbol{Z}}_{{S}_{\rm{a}}}^{\mathbf{T}}{\boldsymbol{X}}_{{S}_{\rm{a}}}{\left({\boldsymbol{X}}_{S}^{\mathbf{T}}{\boldsymbol{X}}_{S}\right)}^{-1}{\boldsymbol{X}}_{S}^{\mathbf{T}}{\boldsymbol{y}}_{S} (12) 式中：
{\widehat{\mu }}_{{\mathrm{M}\mathrm{D}}_{\mathrm{p}\mathrm{l}\mathrm{s}}} 表示分层建模估计的总体均值，{\boldsymbol{\iota }}_{U} 是一个N维向量，每个元素为1/N ，{\boldsymbol{Z}}_{U} 为所有单元对应的卫星数据特征，{\boldsymbol{Z}}_{{S}_{{\rm{a}}}} 为Sa样本集抽样样本对应的卫星遥感特征，{\boldsymbol{X}}_{{S}_{{\rm{a}}}} 为Sa样本集抽样样本对应的无人机遥感特征，{\boldsymbol{X}}_{S} 为样本集S对应的无人机遥感特征。均值方差的估计如（13）所示。V\left({\widehat{\mu }}_{{\mathrm{M}\mathrm{D}}_{\mathrm{p}\mathrm{l}\mathrm{s}}}\right)={\boldsymbol{\iota }}_{U}^{\mathbf{T}}{\boldsymbol{Z}}_{U}\mathrm{C}\mathrm{o}\mathrm{v}\left({\widehat{\boldsymbol{\alpha }}}_{{S}_{{\rm{a}}}}\right){\boldsymbol{Z}}_{U}^{\mathbf{T}}{\boldsymbol{\iota }}_{U} (13) 式中：
\mathrm{C}\mathrm{o}\mathrm{v}\left({\widehat{\boldsymbol{\alpha }}}_{{S}_{{\rm{a}}}}\right) 为模型参数{\widehat{\boldsymbol{\alpha }}}_{{S}_{{\rm{a}}}} 的协方差矩阵，计算公式如（14）所示。\mathrm{C}\mathrm{o}\mathrm{v}\left({\widehat{\boldsymbol{\alpha }}}_{{S}_{\rm{a}}}\right) = \frac{{({\boldsymbol{X}}_{{S}_{\rm{a}}}{\widehat{\boldsymbol{\beta }}}_{s} - {\boldsymbol{Z}}_{{S}_{\rm{a}}}{\widehat{\boldsymbol{\alpha }}}_{{S}_{\rm{a}}} )}^{\mathbf{T}}({\boldsymbol{X}}_{{S}_{\rm{a}}}{\widehat{\boldsymbol{\beta }}}_{S} - {\boldsymbol{Z}}_{{S}_{\rm{a}}}{\widehat{\boldsymbol{\alpha }}}_{{S}_{\rm{a}}} )}{M-( q + 1 )}{\left( {\boldsymbol{Z}}_{{S}_{\rm{a}}}^{\mathbf{T}}{\boldsymbol{Z}}_{{S}_{\rm{a}}} \right)}^{-1} + {\left({\boldsymbol{Z}}_{{S}_{ \rm{a}}}^{\mathbf{T}}{\boldsymbol{Z}}_{{S}_{ \rm{a}}}\right)}^{-1}{\boldsymbol{Z}}_{{S}_{ \rm{a}}}^{\mathbf{T}}\left[{\boldsymbol{X}}_{{S}_{ \rm{a}}}{\left({\boldsymbol{X}}_{S}^{\mathbf{T}}{\boldsymbol{X}}_{S}\right)}^{-1}{\boldsymbol{X}}_{{S}_{ \rm{a}}}^{\mathbf{T}}\right]{\boldsymbol{Z}}_{{S}_{ \rm{a}}}{\left({\boldsymbol{Z}}_{{S}_{ \rm{a}}}^{\mathbf{T}}{\boldsymbol{Z}}_{{S}_{ \rm{a}}}\right)}^{-1} (14) 式中：
{\widehat{\boldsymbol{\beta }}}_{S}={\left({\boldsymbol{X}}_{S}^{\mathbf{T}}{\boldsymbol{X}}_{S}\right)}^{-1}{\boldsymbol{X}}_{S}^{\mathbf{T}}{\boldsymbol{y}}_{S} 为模型参数。2.2 遥感特征选择方法
后4个估测方法都涉及以遥感特征为自变量的统计回归模型建立问题，而无论是卫星遥感数据，还是激光雷达数据都有比较多的备选特征。这些备选特征之间会存在共线性问题，需要进行特征的优选。使用R统计软件VSURF包分别选择LiDAR遥感特征、卫星遥感特征。该包提供了一种自动的方法来根据预测变量的重要性分数选择预测变量[44]，然后结合方差膨胀因子（VIF）以及全子集模型优化策略，利用交叉验证方法选择误差最小的特征组合。
2.3 估测效果评价指标
2.3.1 像元尺度估测效果评价指标
为评价后4个估测方法中所涉及的遥感估测模型的效果，采用留一交叉验证的方法对结果进行评价，选用平均误差（ME）、决定系数（R2）、均方根误差（RMSE）、相对均方根误差（RRMSE）作为像元尺度平均估测效果评价指标，计算公式见（15） ~ （18）。
\mathrm{M}\mathrm{E}=\frac{1}{n}{\sum} _{i=1}^{n}\left({y}_{i}-{\widehat{y}}_{i}\right) (15) {R}^{2}=1-\frac{\displaystyle {\sum} _{i=1}^{n}{\left({y}_{i}-{\widehat{y}}_{i}\right)}^{2}}{\displaystyle {\sum} _{i=1}^{n}{\left({y}_{i}-\overline{y}\right)}^{2}} (16) \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{\displaystyle {\sum} _{i=1}^{n}{\left({y}_{i}-{\widehat{y}}_{i}\right)}^{2}}{n-1}} (17) \mathrm{R}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\left(1-\frac{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}{\overline{y}}\right)\times 100 \% (18) 式中：
{y}_{i} 为样地蓄积量密度实测值；\overline{y} 为实测值对应的均值；{\widehat{y}}_{\mathrm{i}} 为估测值；n为样本点的个数。2.3.2 林场总体MSVD估计精度与相对效率
对5种方法总体结果的精度评价采用标准误（
{S}_{\overline{e}} ）和相对估测精度（P）指标，计算公式如（19）、（20）所示[14,45]。{S}_{\overline{\mathrm{e}}}=\sqrt{V\left(\overline{u}\right)} (19) P=\left(1-\frac{t \cdot {S}_{\overline{\mathrm{e}}}}{\overline{y}}\right)\times 100\% (20) 式中：
V\left(\overline{u}\right) 为均值方差，\overline{y} 为均值，t为可靠性指标，按95%置信区间，t = 1.96。将相对效率（relative efficiency，RE）作为评价不同总体结果估测方法相对效果的指标[14,45]，计算公式如（21）所示。
\mathrm{R}\mathrm{E}=\frac{V\left({\overline{u}}_{1}\right)}{V\left({\overline{u}}_{2}\right)} (21) 式中：
V\left({\overline{u}}_{1}\right) 和V\left({\overline{u}}_{2}\right) 代表两种方法对应的均值方差，当RE > 1，说明V\left({\overline{u}}_{1}\right) 对应的方法效率低于V\left({\overline{u}}_{2}\right) 对应的方法；当RE = 1，说明两种方法效率相同；当RE < 1，说明V\left({\overline{u}}_{1}\right) 对应的方法效率高于V\left({\overline{u}}_{2}\right) 对应的方法。3. 结果与分析
3.1 遥感特征选择结果
利用R语言VSURF包分别对S-2A卫星遥感特征、LiDAR遥感特征进行优选。对于无人机LiDAR数据，当特征数为3时，其RMSE最小（图4a），此时，对应特征为Hmean、Ip99以及R2H；对于S-2A数据，当特征数为4时，其RMSE最小（图4b），对应特征为B2、B2ME、MCARI指数以及B12COR。特征选择后保留的遥感特征见表4。
![]()
图 4 遥感特征选择折线代表值的变化趋势。The broken line represents the trend of value.Figure 4. Feature selection of remote sensing表 4 遥感特征优选后保留的特征Table 4. Remotes sensing features selected after optimum feature selection数据源
Data source特征选择结果
Result of feature selectionS-2A B2，MCARI，B2ME，B12COR LiDAR Hmean，Ip99，R2H 3.2 遥感估测模型的像元尺度估测精度
以S-2A多光谱遥感特征为自变量，以样地蓄积量密度为因变量建立的估测模型（S-V）的精度验证结果见图5b，决定系数R2为0.21，RMSE为81.23 m3/hm2，ME为−0.25 m3/hm2，RRMSE为59.81%。而以LiDAR遥感特征为自变量，以样地蓄积量密度为因变量建立的估测模型（L-V）的精度验证结果见图5a，决定系数R2为0.86，RMSE为33.12 m3/hm2，ME为−0.06 m3/hm2，RRMSE为84.42%。精度指标相比S-2A，R2提高了0.65，RMSE降低了48.11 m3/hm2，ME降低了0.19 m3/hm2，RRMSE提高了24.61%。以LiDAR估测的蓄积量密度为因变量，以S-2A多光谱遥感特征为自变量建立估测模型（S-L-V），估测精度验证结果见图5c，决定系数R2仅提高了0.07，估测精度远低于以LiDAR特征为自变量建立的模型。
![]()
图 5 遥感特征建模估测模型精度实线为1∶1验证线。图中RMSE和ME的单位均为m3/hm2。The solid line is 1∶1 verification line.The unit of RMSE and ME in the figure is m3/ha.Figure 5. Remote sensing feature modeling to estimate model accuracy总之，只要以S-2A多光谱遥感特征作为自变量建立模型估测森林蓄积量密度，无论因变量是样地蓄积量密度还是LiDAR估测得到的蓄积量密度，估测精度都很低。这主要是由于卫星多光谱遥感特征对森林蓄积量不太敏感，两者之间的相关性很低，而且光学遥感探测森林结构容易出现信号饱和问题。该结果与已有研究[15,46-47]的结论是一致的。
3.3 总体MSVD估计精度
如表5所示：5种方法总体结果有一定差别，DBp、MDps、MAps、HYpl、MDpls 5种方法估测总体蓄积均值分别为212.54、202.09、202.38、210.07以及208.96 m3/hm2，仅利用样地的DBp方法结果方差最大（107.51 m3/hm2），当加入全覆盖S-2A数据时，MDps与MAps方法的方差均减少，减少了31.33与33.96 m3/hm2，精度提高1.10%与1.25%。
相对于样地−全覆盖S-2A数据协同模式，采用样地-LiDAR抽样数据协同模式的方法精度更高，HYpl方法相比MDps与MAps方法，方差分别减少了54.76与52.13 m3/hm2，精度提高了4.81%与4.66%。
采用样地−抽样LiDAR数据−全覆盖S-2A数据协同模式的MDpls方法精度最高，均值方差为19.95 m3/hm2，精度比HYpl提高0.10%，比MDps与MAps提高4.91%与4.76%，比DBp提高6.01%，虽然该模式可提高总体均值估计精度，但与采用样地−抽样LiDAR数据协同的HYpl相比，提高幅度较小，这主要是由于S-2A遥感特征对蓄积量不够敏感，对应的估测模型精度低导致的。
表 5 5种方法的总体均值估计结果和精度Table 5. Results and accuracy of total mean estimation of the five methods方法
Method总体均值/（m3·hm−2）
Total mean/(m3·ha−1)均值方差/（m3·hm−2）
Mean variance/(m3·ha−1)标准误/（m3·hm−2）
Standard error/(m3·ha−1)估测精度
Estimation accuracyDBp 212.54 107.51 10.37 90.44% MDps 202.09 76.18 8.72 91.54% MAps 202.38 73.55 8.58 91.69% HYpl 210.07 21.42 4.63 96.35% MDpls 208.96 19.95 4.47 96.45% 3.4 总体MSVD估计相对效率
各个方法之间的相对效率结果如图6所示：DBp方法相对于其他4种方法均为负效率（RE均大于1），其中，MDpls方法估计效率最高（REDBp,MDpls = 5.39），HYpl方法次之（REDBp,HYpl = 5.02），DBp相对于MDps与MAps的RE分别为1.41与1.46，可见无论光学数据还是LiDAR数据的加入，估计效率均有所提高。5种方法中，其他4种方法相对于MDpls方法的RE均大于1（REDBp,MDpls = 5.39，REMDps,MDpls = 3.82，REMAps,MDpls = 3.69，REHYpl,MDpls = 1.07），可见MDpls方法效率最高。HYpl相对于MDpls的RE略大于1，说明估计效率低于MDpls，但比较接近；HYpl估计效率远远高于其他3种方法（REDBp,HYpl = 5.02，REMAps,HYpl = 3.43，REMDps,HYpl = 3.56）。包含LiDAR数据的HYpl与MDpls方法相对于包含S-2A数据的MDps与MAps方法均为正效率（REMAps,HYpl = 3.43，REMDps,HYpl = 3.56，REMDps,MDpls = 3.82，REMAps,MDpls = 3.69），显然LiDAR数据比光学数据更能有效提高总体估计效率。MDps与MAps方法之间的RE接近1，但MAps的效率微高于MDps（REMDps,MAps = 1.04）。
4. 讨 论
近年来，激光雷达数据被广泛用于森林资源监测，且精度较高[27,48-49]，但成本高问题限制了该技术的大范围应用，因此部分学者利用LiDAR抽样观测数据，通过天空地协同实现监测目标[11,14-15,50]，这为在有限经费支撑条件下，提高监测效率提供了可行思路。本研究对适用天空地多源数据应用的MDps、MAps、HYpl、MDpls 4种方法以及传统设计推断DBp方法共5种方法进行了林场总体MSVD估计效果比较评价。
比较评价结果表明5种方法的估计精度均在90%以上，其中HYpl与MDpls方法精度达96%以上，可满足森林资源监测的总体精度要求[6,51]。另外，5种方法中，利用了LiDAR数据的HYpl与MDpls 2种方法精度都高于仅基于样地、样地−卫星遥感数据结合的DBp、MDps以及MAps 3种方法，该结果与Saarela等和Puliti等的研究结果一致[7,15,17]。虽然样地蓄积量密度和S-2A卫星遥感特征之间的相关性不高，但在样地的基础上加入卫星遥感数据后，总体估计精度也有所提高（MDps与MAps精度分别提高1.10%与1.25%；REDBp,MDps = 1.41；REDBp,MAps = 1.46）。由于多光谱卫星遥感数据通常都可以免费获取，增加多光谱卫星数据并不会大幅度增加监测成本，值得在实际调查监测业务中推广应用。样地−抽样无人机LiDAR的协同模式对总体MSVD的估计精度达到96.35%，虽比样地−抽样无人机−卫星遥感协同模式的精度略低（REHYpl,MDpls = 1.07），但差别不大，在实际应用中，若只对总体蓄积量密度进行估计，采用样地−无人机LiDAR抽样的协同模式就足够。
需要特别指出的是，这5种方法中有3种方法（DBp、MAps、HYpl）需要以概率抽样获取观测数据。DBp、MAps都要求样地数据是以概率抽取的，而HYpl要求LiDAR数据是以概率抽取的（但并不要求样地数据按概率抽取）。本研究无人机和样地数据的获取就采用了系统抽样观测的思路，但在实际LiDAR和样地数据获取时做了一些方案调整，因此并不严格满足系统抽样条件，这会对这3种方法的应用产生一定负面影响，本研究假设这些不足不会对结论产生影响。但实际应用中应注意样地、无人机数据的获取应严格采用系统抽样方法抽取样本进行观测。
由于本研究获取的样地数量较少，在试验过程中并未考虑分别优势树种类型进行估计，而是将所有类型合并（不分层）进行总体参数估计。实际应用中可以按优势树种类型分层建立模型进行总体参数的估计，理论上可进一步提高总体参数估计精度，但需要对各优势树种类型分别抽取足够多的样本进行样地调查。本研究中DBp方法的方差为抽样误差，并未考虑样地蓄积量密度计算的不确定性；另外4种方法所采用的估测模型都属于线性模型，均值方差主要为模型带来的误差，同样未考虑样地蓄积量密度计算的不确定性，也未考虑由LiDAR估测的蓄积量密度之间的空间自相关带来的不确定性。国内外学者已研发了非线性估测模型和考虑了空间自相关性的分层估测模型和不确定性估计方法[18,30,52]，未来应有针对性地开展相关新技术新方法的应用试验和比较评价研究。
5. 结 论
本研究以旺业甸实验林场为研究区，以林场针叶人工林为总体，针对1种只应用样地数据的模式与3种将样地与遥感数据协同应用的模式（样地−卫星多光谱遥感、样地−无人机LiDAR抽样观测、样地−无人机LiDAR抽样观测−卫星多光谱遥感），对5种林场总体MSVD估计方法进行了比较评价。研究结果表明：（1）和只利用样地数据的估计方法相比，将遥感作为辅助变量建立估测模型，无论是采用对林场全覆盖但对蓄积量不够敏感的S-2A多光谱遥感数据，还是采用抽样式获取的对蓄积量很敏感的LiDAR数据，都可有效提高林场总体MSVD的估测精度。（2）涉及遥感数据应用的4种方法，估计精度最高的为MDpls，其次为HYpl，这2种方法都包含了LiDAR遥感抽样观测数据的应用，都是适合应用于林场总体MSVD估计的年度监测方法。（3）可实现天空地3种观测数据协同应用的方法（MDpls）估测精度和相对效率最高，可作为林场森林蓄积量年度监测的首选方法。
-
![]()
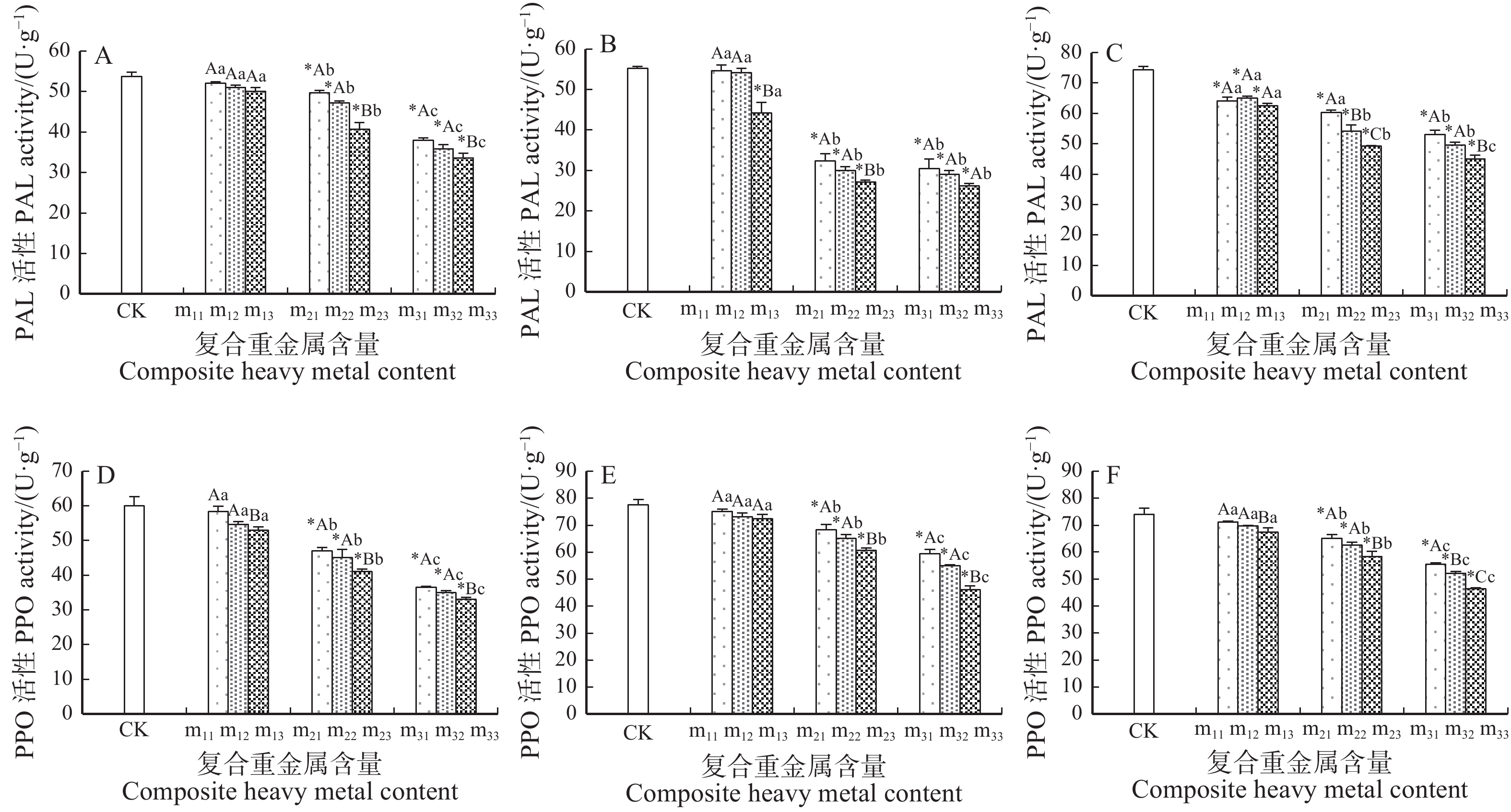
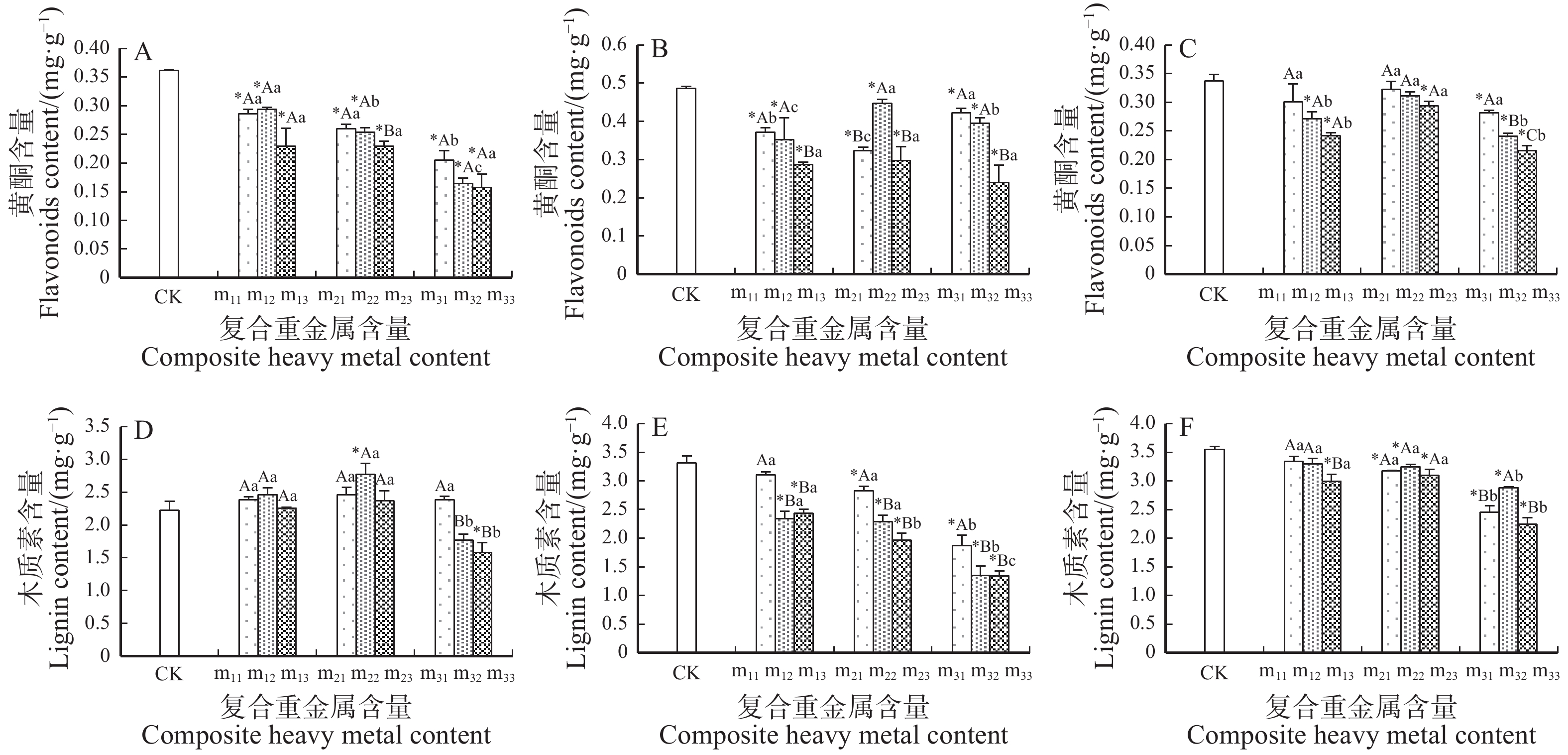
图 1 Cd、Zn胁迫下银中杨叶片中的PAL和PPO活性
数据均为平均值 ± 标准差（n = 3）；*表示复合重金属胁迫组与对照组之间差异显著（P < 0.05）；不同大写字母表示Cd含量相同时胁迫组之间差异显著（P < 0.05）；不同小写字母表示Zn含量相同时胁迫组之间差异显著（P < 0.05）；A和D为胁迫30 d；B和E为胁迫40 d；C和F为胁迫50 d。下同。The data annotation in the picture is average value ± standard deviation (n = 3); the asterisk (*) indicates that there is a significant difference between the treatment and control (P < 0.05); different capital letters mean significant difference among treatments when the concentration of Cd is the same (P < 0.05); different lowercase letters mean significant difference among treatments when the concentration of Zn is the same (P < 0.05); A and D mean under stress for 30 days; B and E mean under stress for 40 days; C and F mean under stress for 50 days. The same below.
Figure 1. PAL and PPO activities in the PAB leaves under Cd and Zn stress
![]()
图 2 Cd、Zn胁迫下银中杨叶片中的TI和CI活性
Figure 2. TI and CI activities in the PAB leaves under Cd and Zn stress
![]()
图 3 Cd、Zn胁迫下银中杨叶片中的黄酮和木质素含量
OD值为280 nm处的吸收值。OD value is the absorption value at 280 nm.
Figure 3. Flavonoid and lignin content in the PAB leaves under Cd and Zn stress
表 1 Cd和Zn复合胁迫实验设计
Table 1 Experimental design of Cd-Zn combined stress
项目 Item CK m11 m12 m13 m21 m22 m23 m31 m32 m33 Cd含量 Cd content 0 0.5 0.5 0.5 1.5 1.5 1.5 2.5 2.5 2.5 Zn含量 Zn content 0 300 500 700 300 500 700 300 500 700 注：CK代表对照组；m11代表Cd 0.5 和Zn 300 mg/kg复合胁迫组；m12代表Cd 0.5 和Zn 500 mg/kg复合胁迫组；m13代表Cd 0.5 和Zn 700 mg/kg复合胁迫组；m21代表Cd 1.5 和Zn 300 mg/kg复合胁迫组；m22代表Cd 1.5 和Zn 500 mg/kg复合胁迫组；m23代表Cd 1.5 和Zn 700 mg/kg复合胁迫组；m31代表Cd 2.5 和Zn 300 mg/kg复合胁迫组；m32代表Cd 2.5 和Zn 500 mg/kg复合胁迫组；m33代表Cd 2.5 和Zn 700 mg/kg复合胁迫组。下同。Notes: CK is control group; m11 represents Cd 0.5 and Zn 300 mg/kg combined stress group; m12 represents Cd 0.5 and Zn 500 mg/kg combined stress group; m13 represents Cd 0.5 and Zn 700 mg/kg combined stress group; m21 represents Cd 1.5 and Zn 300 mg/kg combined stress group; m22 represents Cd 1.5 and Zn 500 mg/kg combined stress group; m23 represents Cd 1.5 and Zn 700 mg/kg combined stress group; m31 represents Cd 2.5 and Zn 300 mg/kg combined stress group; m32 represents Cd 2.5 and Zn 500 mg/kg combined stress group; m33 represents Cd 2.5 and Zn 700 mg/kg combined stress group. The same below. 
下载: 导出CSV
-
[1] 李凤果, 陈明, 师艳丽, 等. 我国农用地土壤污染修复研究现状分析[J]. 现代化工, 2018, 38(12):4−9. Li F G, Chen M, Shi Y L, et al. Research progress of soil contamination restoration in agricultural land in China[J]. Modern Chemical Industry, 2018, 38(12): 4−9.
[2] Kim H T, Kim J G. Uptake of cadmium, copper, lead, and zinc from sediments by an aquatic macrophyte and by terrestrial arthropods in a freshwater wetland ecosystem[J]. Archives of Environmental Contamination & Toxicology, 2016, 71(2): 1−12.
[3] 王锦文, 白秀, 陈锦峰, 等. 复合重金属Pb/Zn对香樟生理特征的影响[J]. 安徽农业科学, 2009, 37(21):10253−10254. doi: 10.3969/j.issn.0517-6611.2009.21.166 Wang J W, Bai X, Chen J F, et al. Effects of complex heavy metals Pb/Zn on the physiological characteristics of Paulowniu fortunel (seem) hems[J]. Journal of Anhui Agricultural Sciences, 2009, 37(21): 10253−10254. doi: 10.3969/j.issn.0517-6611.2009.21.166
[4] Jia X, Zhao Y H, Liu T, et al. Leaf defense system of Robinia pseudoacacia L. seedlings exposed to 3 years of elevated atmospheric CO2 and Cd-contaminated soils[J]. Science of The Total Environment, 2017, 605−606: 48−57.
[5] 杨期和, 赖万年, 杨和生, 等. 土壤Cd污染的生物修复[J]. 嘉应学院学报, 2014, 32(5):58−65. doi: 10.3969/j.issn.1006-642X.2014.05.012 Yang Q H, Lai W N, Yang H S, et al. Bioremediation of Cd contaminated soil[J]. Journal of Jiaying University, 2014, 32(5): 58−65. doi: 10.3969/j.issn.1006-642X.2014.05.012
[6] 杜锁军, 戴艳, 谢东俊, 等. 土壤Zn污染及其治理措施评述[J]. 污染防治技术, 2009, 22(3):87−90. Du S J, Dai Y, Xie D J, et al. The introduction of Zn pollution in soil and its control mesures[J]. Pollution Control Techonology, 2009, 22(3): 87−90.
[7] 吴志能, 谢苗苗, 王莹莹. 我国复合污染土壤修复研究进展[J]. 农业环境科学学报, 2016, 35(12):2250−2259. doi: 10.11654/jaes.2016-0863 Wu Z N, Xie M M, Wang Y Y. Remediation of soils with combined pollution in China: a review[J]. Journal of Agro-Environment Science, 2016, 35(12): 2250−2259. doi: 10.11654/jaes.2016-0863
[8] 刘艳丽, 吴凤霞, 徐莹, 等. 杨树修复重金属污染土壤的研究进展[J]. 林业科学, 2012, 48(9):139−144. Liu Y L, Wu F X, Xu Y, et al. Research progress in the remediation of heavy metal contaminated soils with Populus[J]. Scientia Silvae Sinicae, 2012, 48(9): 139−144.
[9] 齐洪涛, 白莉萍, 陆海波, 等. 堆肥污泥对不同杨树品种重金属富集变化的影响[J]. 东北林业大学学报, 2014, 42(11):22−27. doi: 10.3969/j.issn.1000-5382.2014.11.006 Qi H T, Bai L P, Lu H B, et al. Effects of fertilizer sludge on heavy metal concentration in different poplar varieties[J]. Journal of Northeast Forestry University, 2014, 42(11): 22−27. doi: 10.3969/j.issn.1000-5382.2014.11.006
[10] 国家环境保护局, 国家技术监督局. GB15618—1995 土壤环境质量标准[S]. 北京: 中国标准出版社, 1995. State Department of Environmental Conservation, State Bureau of Technical Supervision. GB15618 —1995 soil environmental quality standard[S]. Beijing: China Standards Press, 1995.
[11] 崔伟婵, 李霜雯, 严善春. 不同光照下外源茉莉酸类物质对兴安落叶松防御蛋白的影响[J]. 东北林业大学学报, 2016, 44(9):78−81. doi: 10.3969/j.issn.1000-5382.2016.09.017 Cui W C, Li S W, Yan S C. Effects of exogenous jasmonic acids on defense protein of Larix gmelinii under different illumination[J]. Journal of Northeast Forestry University, 2016, 44(9): 78−81. doi: 10.3969/j.issn.1000-5382.2016.09.017
[12] 姜虹, 严善春, 薛羿, 等. 落叶松林型对其针叶内几种防御蛋白活力和次生代谢物含量的影响[J]. 林业科学研究, 2018, 31(3):24−28. Jiang H, Yan S C, Xue Y, et al. Effects of forest type on activity of several defense proteins and contents of secondary metabolites in larch needles[J]. Forest Research, 2018, 31(3): 24−28.
[13] 王杰, 孟昭军, 王琪, 等. 外源茉莉酸诱导方式对长白落叶松针叶内防御蛋白活力的影响[J]. 东北林业大学学报, 2015, 43(5):84−89. doi: 10.3969/j.issn.1000-5382.2015.05.017 Wang J, Meng Z J, Wang Q, et al. Effects of exogenous jasmonic acid induction on defense protein activity in Larch needles[J]. Journal of Northeast Forestry University, 2015, 43(5): 84−89. doi: 10.3969/j.issn.1000-5382.2015.05.017
[14] 任琴, 胡永建, 李镇宇, 等. 受害马尾松木质素含量及其过氧化物酶活性[J]. 生态学报, 2007,27(11):4895−4899. doi: 10.3321/j.issn:1000-0933.2007.11.060 Ren Q, Hu Y J, Li Z Y, et al. Content variation of lignin and peroxidase activities from damaged Pinus massioniana[J]. Acta Ecologica Sinica, 2007,27(11): 4895−4899. doi: 10.3321/j.issn:1000-0933.2007.11.060
[15] 刘江, 周荣琪. 竹叶提取物总黄酮含量测定方法的改进[J]. 食品科技, 2005(7):76−79. doi: 10.3969/j.issn.1005-9989.2005.07.023 Liu J, Zhou R Q. Improved meansuration for general flavone of banboo leaves extract[J]. Food Science and Technology, 2005(7): 76−79. doi: 10.3969/j.issn.1005-9989.2005.07.023
[16] Fuerst E P, Okubara P A, Anderson J V, et al. Polyphenol oxidase as a biochemical seed defense mechanism[J/OL]. Frontiers in Plant Science, 2014, 5 (2014−12−05) [2018−10−12]. https://doi.org/10.3389/fpls.2014.00689.
[17] 王光达, 黄初女, 吴委林, 等. 不同玉米品种对大斑病的抗性与相关防御酶活性的关系研究[J]. 玉米科学, 2014, 22(5):146−152. doi: 10.3969/j.issn.1005-0906.2014.05.028 Wang G D, Huang C N, Wu W L, et al. Defense enzyme activities and the resistance to northern leaf blight of different hybrids in maize[J]. Journal of Maize Sciences, 2014, 22(5): 146−152. doi: 10.3969/j.issn.1005-0906.2014.05.028
[18] 樊艳平, 成小芳, 王宏民, 等. 蛋白酶抑制剂对绿豆象幼虫中肠蛋白酶活性的影响[J]. 应用生态学报, 2018, 29(5):1660−1666. Fan Y P, Cheng X F, Wang H M, et al. Effects of protease inhibitors on the activities of midgut proteases in Callosobruchus chinensis (Linnaeus) larvae[J]. Chinese Journal of Applied Ecology, 2018, 29(5): 1660−1666.
[19] 赵爱平, 孙聪, 展恩玲, 等. 蛋白酶抑制剂对梨小食心虫幼虫中肠蛋白酶活性的影响[J]. 昆虫学报, 2016, 59(10):1069−1078. Zhao A P, Sun C, Zhan E L, et al. Effects of protease inhibitors on the activities of midgut proteases of larval Grapholitha molesta (Lepidoptera: Tortricidae)[J]. Acta Entomologica Sinica, 2016, 59(10): 1069−1078.
[20] 赵微, 尹静, 詹亚光, 等. 温度胁迫对白桦悬浮细胞中三萜积累及防御酶活性的影响[J]. 中国生物工程杂志, 2013, 33(2):34−40. Zhao W, Yin J, Zhan Y G, et al. Effects of temperature stress on triterpene accumulation and defense enzyme activity in suspension cells of Betula platyphylla[J]. China Biotechnology, 2013, 33(2): 34−40.
[21] 鲁艺芳, 石蕾, 严善春. 不同光照强度对兴安落叶松几种主要防御蛋白活力的影响[J]. 生态学报, 2012, 32(11):3621−3627. Lu Y F, Shi L, Yan S C. Effects of different light intensities on activities of the primary defense proteins in needles of Larix gmelinii[J]. Acta Ecologica Sinica, 2012, 32(11): 3621−3627.
[22] Jiang D, Wang Y Y, Dong X W, et al. Inducible defense responses in Populus alba berolinensis to Pb stress[J]. South African Journal of Botany, 2018, 119: 295−300. doi: 10.1016/j.sajb.2018.09.030
[23] 郭光艳, 柏峰, 刘伟, 等. 转录因子对木质素生物合成调控的研究进展[J]. 中国农业科学, 2015, 48(7):1277−1287. Guo G Y, Bo F, Liu W, et al. Advances in research of the regulation of transcription factors of lignin biosynthesis[J]. Scientia Agricultura Sinica, 2015, 48(7): 1277−1287.
[24] 诸姮, 胡宏友, 卢昌义, 等. 植物体内的黄酮类化合物代谢及其调控研究进展[J]. 厦门大学学报(自然科学版), 2007, 46(增刊1): 136−143. Zhu H, Hu H Y, Lu C Y, et al. Advances in the Study of flavonoids metabolism and regulation in plants[J]. Journal of Xiamen University (Natural Science), 2007, 46(Suppl. 1): 136−143.
[25] 张凯, 徐波, 孟昭军, 等. 铜、镉胁迫对杨树叶片中防御蛋白活性的影响[J]. 东北林业大学学报, 2014, 42(11):43−46. doi: 10.3969/j.issn.1000-5382.2014.11.011 Zhang K, Xu B, Meng Z J, et al. Effect of copper and cadmium on defensive protein activity in poplar leaves[J]. Journal of Northeast Forestry University, 2014, 42(11): 43−46. doi: 10.3969/j.issn.1000-5382.2014.11.011
[26] 姜礅, 王月月, 严善春. 锌胁迫对银中杨生长发育和化学防御的影响[J]. 北京林业大学学报, 2018, 40(11):42−48. Jiang D, Wang Y Y, Yan S C. Effects of Zn stress on growth development and chemical defense of Populus alba ‘Berolinensis’ seedlings[J]. Journal of Beijing Forestry University, 2018, 40(11): 42−48.
[27] Jiang D, Yan S. Effects of Cd, Zn or Pb stress in Populus alba ‘Berolinensis’ on the development and reproduction of Lymantria dispar[J]. Ecotoxicology, 2017, 26(1): 1−9. doi: 10.1007/s10646-016-1742-7
[28] 张凯, 周艳涛, 王皙玮, 等. 铜、镉胁迫对舞毒蛾排毒代谢酶的影响[J]. 北京林业大学学报, 2016, 38(2):61−67. Zhang K, Zhou Y T, Wang X W, et al. Effects of copper and cadmium stress on the activities of detoxifying metabolic enzymes in Lymantria dispar[J]. Journal of Beijing Forestry University, 2016, 38(2): 61−67.
[29] 姜礅, 王月月, 严善春. 银中杨各部位对Cd、Zn、Pb的富集特性[J]. 北京林业大学学报, 2018, 40(1):83−88. Jiang D, Wang Y Y, Yan S C. Accumulation characteristics in all parts of Populus alba ‘Berolinensis ’ to cadmium, zinc, and lead[J]. Journal of Beijing Forestry University, 2018, 40(1): 83−88.
-
期刊类型引用(4)
1. 高郯，张铎，卢杰，王超，李江荣. 色季拉山高山松林降雨再分配及重金属元素的时空特征研究. 西南林业大学学报(自然科学). 2022(01): 115-123 . 
百度学术
2. 陈新宇，孟景祥，周先清，袁虎威，钮世辉，李悦. 油松地理种群针叶形态解剖与生理指标遗传变异分析. 北京林业大学学报. 2019(07): 19-30 . 本站查看
3. 金微微，张会慧，滕志远，孙广玉，许楠. 乡土风箱果和紫叶风箱果及其杂交种F_1叶片的光合功能研究. 中南林业科技大学学报. 2018(04): 33-39 . 百度学术
4. 周丽，陈诗，朱存福，许玉兰，李悦，李伟，蔡年辉. 高山松不同种源苗木在云南松生境下的生物量与生长分析. 广东农业科学. 2017(02): 68-75 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 2004
- HTML全文浏览量: 619
- PDF下载量: 22
- 被引次数: 8
